流体横掠圆柱数值模拟流态转换临界雷诺数的研究

李永光, 樊鹏远, 白曾凯, 李晶晶, 王新程, 谢红振

(上海电力学院 能源与机械工程学院, 上海 200090)

流体横掠圆柱的流态变化非常复杂,其流动状态主要取决于雷诺数Re的大小。当Re很小时,圆柱扰流均为层流,且尾部有一对不会脱落的旋涡;Re逐渐增大后,圆柱尾部的一对层流旋涡会周期性地脱落;当Re继续增大时,扰流的流态就会发生转捩变为紊流。在过去的几十年中,国内外学者对流体横掠圆柱进行了试验研究,分别得出了不同Re下圆柱扰流的流动特性,这些特性包括涉及旋涡脱落频率的斯特劳哈数St,阻力系数Cd,以及分离点的位置等[1-9]。

在数值模拟研究方面,学者们分别采用直接模拟、大涡模拟和雷诺时均模拟等方法对流体横掠圆柱工况进行了数值计算研究,得到了不同雷诺数工况下,流体横掠圆柱体后的尾流流动特性[10-21]。

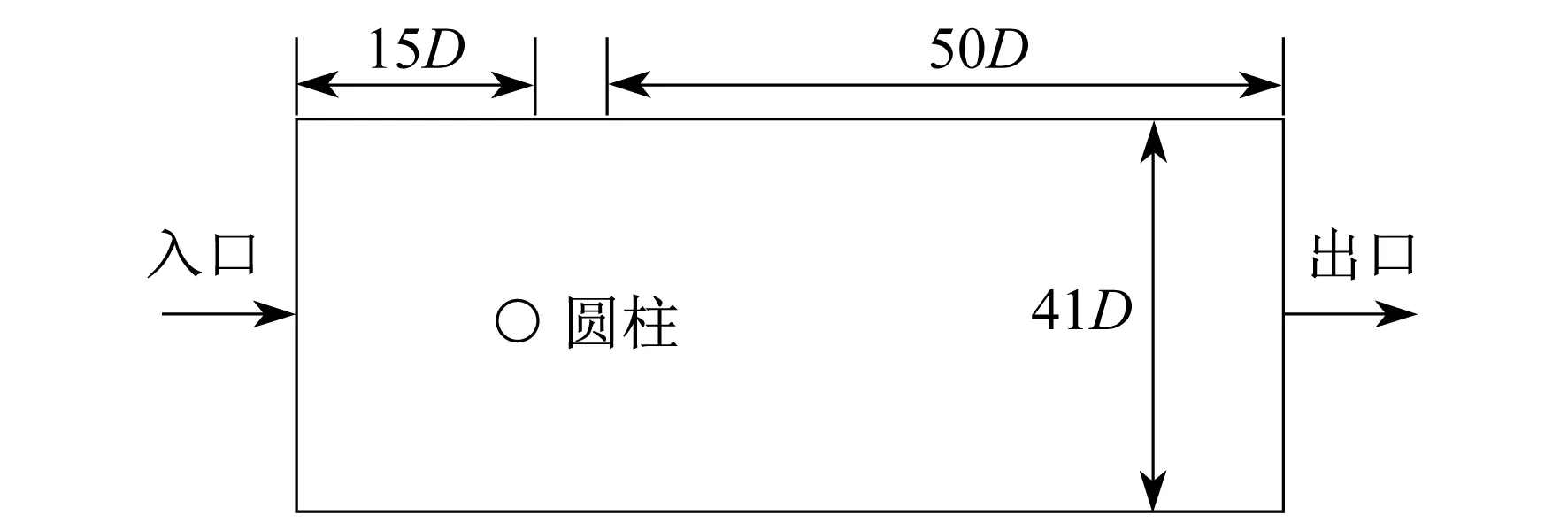
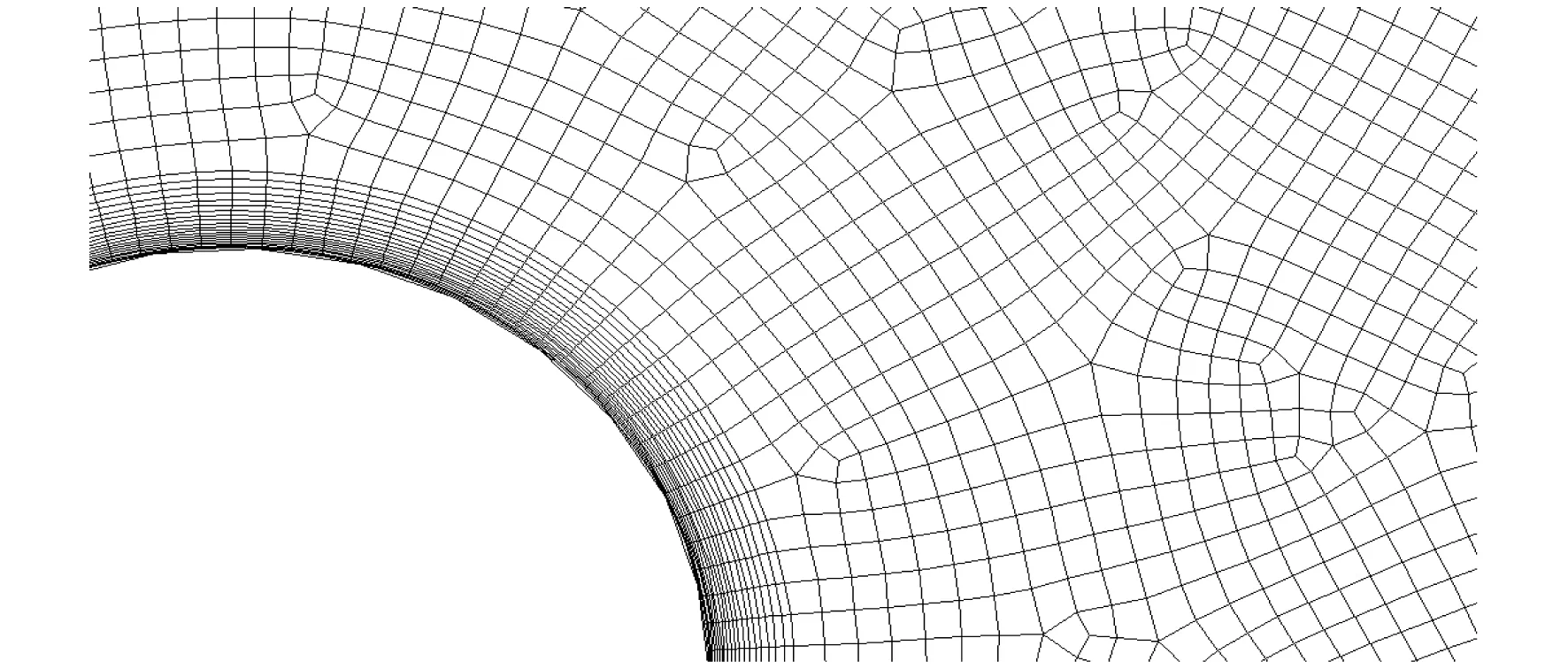
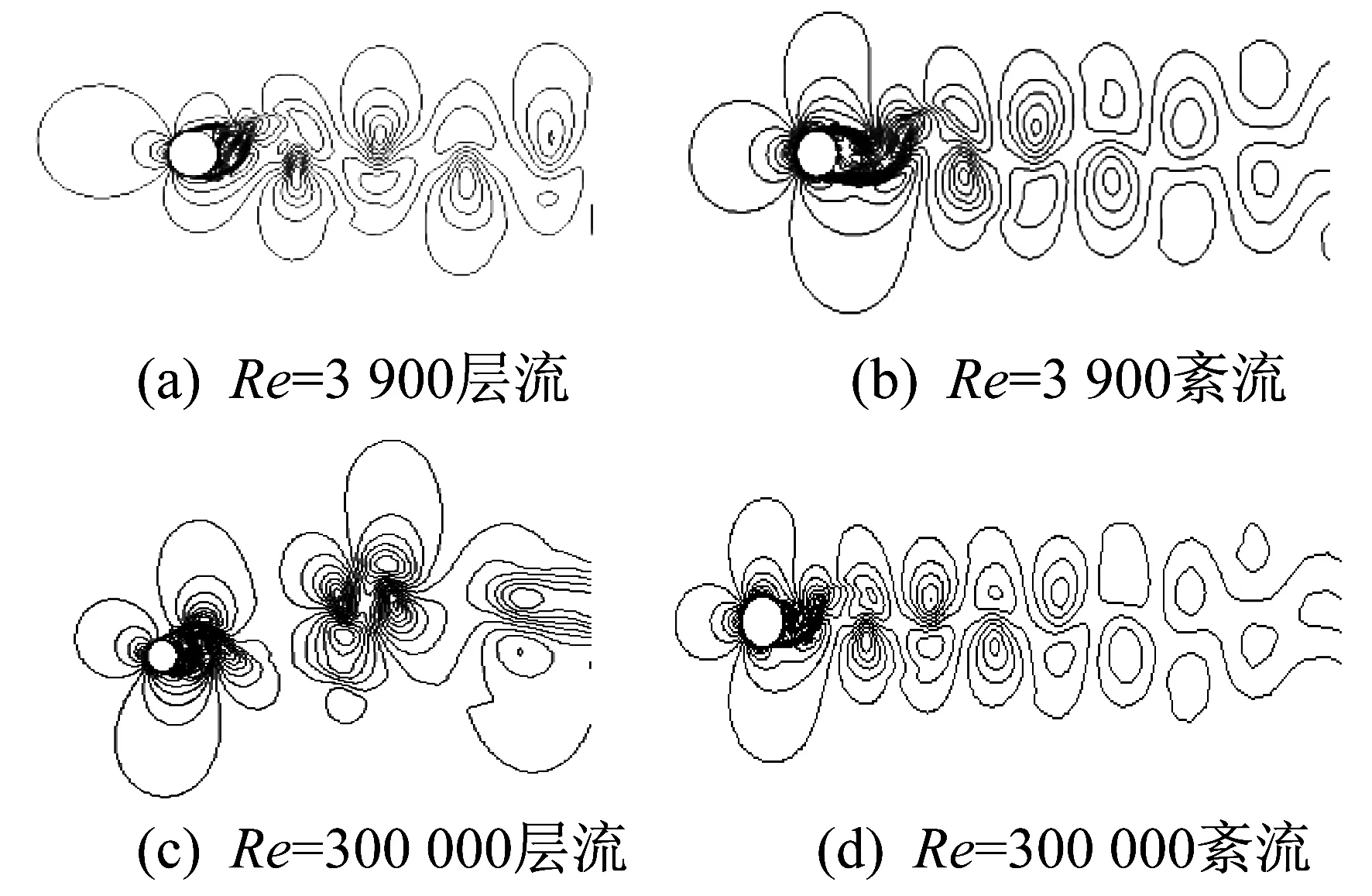
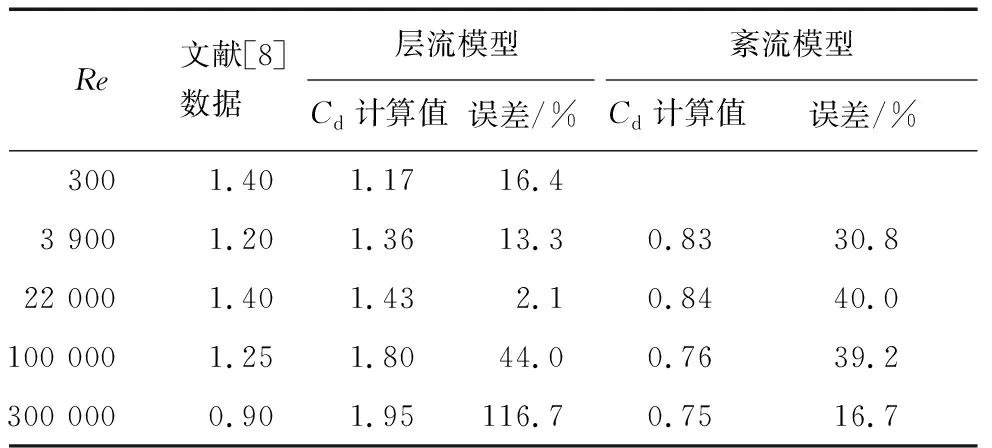
我们知道,试验研究通常在截面积有一定大小的通道中进行。当Re≤2 000时,来流为层流;当2 000

对流体横掠平板的流动,当从平板前缘点开始计算沿流动方向长度为特征长度的雷诺数小于100 000时,仍可作为层流处理[22]。根据边界层理论,边界层外流体也可作为层流处理。如果圆柱扰流也存在某个临界雷诺数,当小于这个临界雷诺数时,就可以用层流模型进行数值模拟,那么找出这个临界雷诺数对工程实际具有重大意义。

本文运用CFD软件,分别采用层流和RNGk-ε紊流模型对亚临界雷诺数下的流体横掠圆柱进行了数值模拟,计算得出了两种模型在不同雷诺数时的阻力系数和斯特劳哈数,同时模拟出了流体横掠圆柱过程中的漩涡脱落、流场演变等情况;并将研究结果与试验值进行了比较,得出了临界雷诺数的大小。研究结果可为工程实际的计算提供参考。

1 流体横掠圆柱计算模型的建立

1.1 物理模型及简化条件

计算区域如图1所示[23]。圆柱直径为D,圆柱距离流体入口15D,距离出口50D,距离上下边界面均为20D。

图1 流体横掠圆柱示意

通道入口来流为均匀来流,工质为空气,设其为不可压缩流体;不考虑重力对此过程的影响;在管轴方向上物理量的变化量忽略不计,也就是将物理模型简化为二维模型。

1.2 数学模型

不可压缩黏性流体的运动可用Navier-Stokes方程[24]来描述,连续性方程与动量方程为

(1)

式中:ui,uj——x方向和y方向的速度分量;

t——流动时间;

ρ——流体密度;

p——压力;

ν——流体动力黏度。

本文采用RNGk-ε模型计算流体横掠圆柱工况。该模型是由标准k-ε模型优化后得出的,由YAKHOT V和ORZAG S A[25]提出。在RNGk-ε模型中,通过大尺度运动和修正后的黏度项体现小尺度的影响,而将这些小尺度运动有系统地从控制方程中去除。其表达式如下

(2)

(3)

式中:k——湍流动能;

Gk——由平均速度梯度引起的k的产生项;

ε——紊流脉动动能耗散率;

μeff=μ+μt,μt=ρCμk2/ε;

αk=αε=1.39;C2ε=1.68。

与标准k-ε模型相比,RNGk-ε模型修正了湍动黏度,考虑了平均流动中的旋转和旋转流动的情况。同时,在ε方程中加入了一项ρε,从而反映了主流的时均应变率Eij,这样该模型中的产生项不仅与流动情况有关,而且在同一问题中还是空间坐标的函数。因此,RNGk-ε模型能更好地处理高应变率和流线弯曲程度较大的流动[26]。

1.3 边界条件

进口面的边界条件设置为速度进口边界条件,流体的来流速度由给定的雷诺数决定;出口面的边界条件设置为压力出口边界条件,出口背压为一个标准大气压;计算区域的上下边界面为对称界面,圆柱壁面为无滑移固壁界面。

2 数值模拟

2.1 网格划分

本文所用的全局网格、计算区域及近壁面网格分别如图2和图3所示。为了更好地计算出近壁区和尾流区的细节,使用分块网格将计算区域分为9个部分,近壁区网格加密,其余部分采用等比网格线,膨胀比为1.03。在圆柱壁面添加20层膨胀比为1.05的边界层网格,并在近壁区采用壁面函数法[23]进行计算。

图2 全局网格和计算区域

图3 近壁面网格

2.2 模拟工况

斯特劳哈数St又被称为旋涡脱落的无量纲频率。其定义为

(4)

式中:f——涡街脱落频率;

D——圆柱直径;

u——来流速度。

1954年,ROSHO根据大量的试验结果,给出了斯特劳哈数的规律[26]。

由经典试验[27]可知,在亚临界雷诺数条件下,St约为0.2。又由式(4)可知,旋涡脱落的频率与流速成反比,所以为了保证计算不同雷诺数的工况时每个涡街脱落周期内包含同样多的时间步长,设置Re与时间步长成反比。此外,选取的时间步长应远小于流动稳定时的旋涡脱落周期,以便在数据中准确识别出完整周期的时长。同时,为了保证尾流充分发展,计算过程要经过足够多的时间步长,本文设置每种工况均计算10 000个时间步长,雷诺数与时间步长的乘积均为3。

3 流动特性模拟结果及分析

本文采用层流模型和RNGk-ε模型分别计算斯特劳哈数,计算值与文献[26]中的试验值如图4所示[26]。

图4 斯特拉赫数的计算值与试验值

阻力系数Cd的定义如下

(5)

式中:Fd——阻力,圆柱表面压力乘圆柱表面积在来流方向上投影的代数和,N。

采用层流模型和紊流模型计算出的涡量等值线如图5所示。

图5 不同雷诺数下的涡量等值线示意

通过检测尾流处两个监测点的速度,得出该工况下的斯特劳哈数。上下监测点的位置在横向距离圆心1.5D,纵向距离中心线0.5D处。以Re=300 000时RNGk-ε紊流模型为例,流动稳定后的检测结果如图6所示。然后由得出的旋涡脱落频率和式(4)计算出斯特劳哈数。阻力系数由FLUENT软件直接计算,即输出圆柱表面个点的压力在来流方向上投影的代数和,此处设置方向矢量为(0,1)。

图6 Re=300 000时监测点速度与

通过数值模拟,计算得出不同雷诺数下的阻力系数Cd和斯特劳哈数St,分别如表1和表2所示。

表1 阻力系数Cd模拟计算结果

表2 斯特劳哈数St模拟计算结果

由表1可以看出,Re在300～22 000范围时,用层流模型计算出的Cd值与试验值均比较接近,最大误差为Re=300时的计算工况,为16.4%。而用紊流RNGk-ε模型计算的误差均较大,最小误差为Re=300 000时的计算工况,为16.7%。

由表2可以看出,用层流模型计算,在Re=300 000时St的误差较大,而用紊流模型计算,计算值均与试验值接近,误差较小。

对阻力系数而言,直到Re=22 000时,仍可采用层流方法模拟,而对St数的计算情况直到Re=100 000时,仍可采用层流方法模拟。究其原因是,阻力系数的大小主要与流过圆柱体的压力损失有关,而压力损失主要与分离点的位置有关,分离点的位置决定了尾流区的大小,尾流区越大,压力损失越大。采用层流模型计算时,由于无法考虑流体质点的脉动效应,因此计算出的分离点靠前,尾流区较大,阻力系数也就偏大。同时,随着雷诺数的增大,紊流特征越来越显著,因此用层流模型计算出的阻力系数偏差就会增加,阻力系数偏大。

St的数值主要与圆柱体表面旋涡脱离的频率有关。当来流速度(或Re)较小时,Re对旋涡脱落频率的影响不大,因此直到Re=100 000时,层流模型计算的St仍与试验值接近。但随着Re的增大,流体质点脉动加剧,分离点的位置前移,旋涡脱落的频率加快,层流模型已完全无法模拟流体质点的剧烈脉动,因此当Re=300 000时,St出现了严重的偏差。

4 结 论

(1) 在计算阻力系数Cd时,可在Re<22 000时采用层流模型,与试验值之间的误差不会超过16.4%。

(2) 在计算斯特劳哈数St时,可在Re<100 000时采用层流模型,但当Re=300 000时,误差较大。