凸函数性质在不等式证明中的应用
徐 建 中
(亳州学院,安徽 亳州 236800)
在数学思想方法中,函数思想是很重要的一种思想方法,其精髓在于利用函数的相关性质对讨论的问题进行推理和论证,进而寻求解决问题的途径。凸函数是一类常见的重要函数,自建立凸函数以来,凸函数这一重要概念已在许多数学分支都得到广泛应用,尤其是在数学分析、函数论、泛函分析,最优化理论等方面有着许多的应用。现行的高等教学教材中也都对函数的凸性做了介绍。凸函数在不等式的研究中尤为重要,而不等式证明最终归结为研究函数的特性,因此研究凸函数的性质十分重要。
1 凸函数的定义、性质及判定定理
1.1 定义
定义1设f(x)定义在区间I上,任意x1,x2∈I,0<α<1,0<β<1,α+β=1,恒有
f(αx1+βx2)≤αf(x1)+βf(x2)
(1)
则称f(x)在I上为下凸函数。若当x1≠x2有严格的不等号成立,则称f(x)为严格的下凸函数。下凸函数简称为凸函数。在式(1)中,若将不等号反向,则称f(x)在I上为上凸函数,当严格的不等号成立时,则称为严格的上凸函数。
1.2 几种等价定义
定义2若f(x)在I上有定义,f(x)称为I上的凸函数,当且仅当
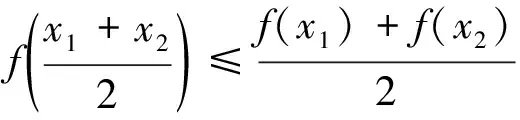
(2)
定义3若f(x)在I上有定义,f(x)称为凸函数,当且仅当
∀x1,x2,…,xn∈I,有
(3)
定义4若f(x)在I上有定义,当且仅当曲线y=f(x)的切线恒保持在曲线的下方,则称y=f(x)为凸函数,若除切点之外,切线严格保持在曲线的下方,则称f(x)为严格的凸函数。
1.3 性质及定理
性质1设f(x)在区间I上为凸函数,对任意的k>0,则kf(x)在区间I上也为凸函数。
性质2设f(x),g(x)在区间I上为凸函数,则f(x)+g(x)是区间I上的凸函数。
性质3设f(x),g(x)在区间I上为凸函数,则线性组合的函数k1f(x)+k2g(x)(k1,k2>0)为区间I上的凸函数。
性质4若f(x),g(x)在区间I上为凸函数,则max{f(x),g(x)}为区间I上的凸函数。
性质5设g(u)是单调递增的凸函数,u=f(x)是凸函数,则复合函数g[f(x)]也是凸函数。
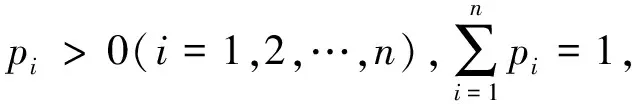
(4)
证明:显然只要证明必要性即可。因为f(x)在I上为凸函数,所以当n=1时,式(4)显然成立;当n=2时,由定义1和式(2)知,式(4)成立。
设当n=k时,式(4)成立,即有:
则当n=k+1时有:
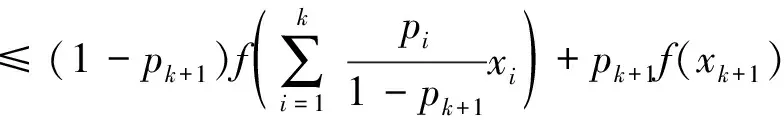
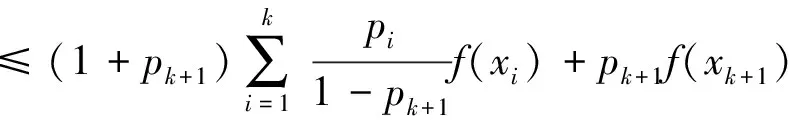
由数学归纳法知,式(4)对一切自然数成立。
2 在不等式证明中的应用
2.1 在Jensen不等式证明中的应用
例1证明n个正数的倒数的算术平均值不小于这n个数的算术平均值的倒数。
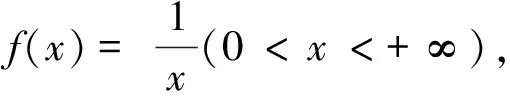
(5)
例2证明:n个正数的算术平均值不小于这n个正数的几何平均值。

于是得
(6)
例3设xi>0(i=1,2,…,n),证明:
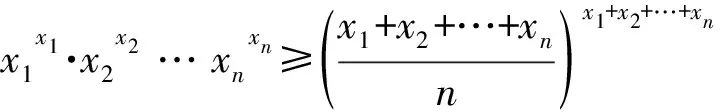
(7)
(8)
(3)x1x1+x2x2+…+xnxn≥
(9)
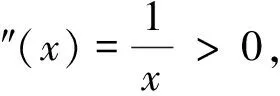
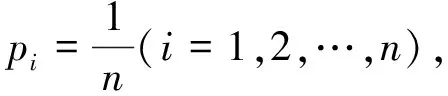
即
所以有
(xi>0,i=1,2,…,n)
(2) 由式(6)、(7)成立,易知式(8)成立。
(3) 令f(x)=xx(0 因为 f′(x)=xx(1+lnx) 所以,f(x)=xx在(0,+∞)上是凸函数。 即 证明:令f(x)=xα(α>1,0 所以f(x)=xα在(0,+∞)上为凸函数。由f(x)在I上为凸函数的定义及定理1知,当ti>0时, 当xi∈(a,b)(i=1,2,…,n)时,有: 得 当aiα与biβ成比例时,即aiα=kbiβ(k为正整数,i=1,2,…,n) 当aiα与biβ不成比例时,ti不全相等,又因为f(x)=xα在(0,+∞)内为严格凸函数,故严格不等号成立。 例5若xi>0,yi>0,i=1,2,…,n,则有 证明:由Cauchy不等式,则有: 即 凸函数的应用领域非常广泛,特别是在不等式的证明中,运用凸函数解题显得巧妙而简练。利用函数的凸性来证明不等式,通常需要构造适当的凸函数,再利用函数凸性的定义及性质,将一些琴生不等式、Cauchy不等式等转化为研究函数性质的性态,从而使不等式简化,进而得到证明。
2.2 在Holder不等式证明中的应用
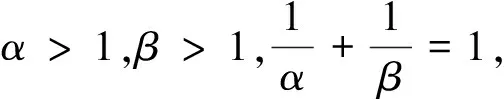
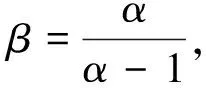
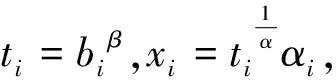
2.3 在Cauchy不等式证明中的应用
3 结 语

