身体姿势识别倒置效应量的连续性变化*

陶维东 陶晓丽

(湖州师范学院教师教育学院，湖州 313000)

1 前言

自然界物体种类繁多，各种类型的物体，其识别时加工方式是否一样？这是物体识别研究领域中最基础的问题之一。几十年来，大量研究往往采用一个最基本的操作范式：倒置呈现，并通过对比各种刺激材料识别时是否产生倒置效应(Yin，1969)来推断被试识别各个刺激材料时所采用的加工方式。与普通物体识别相比，面孔倒置呈现后被试的识别成绩显著下降的现象称为倒置效应。倒置效应的存在使得众多研究者认为，面孔识别与普通物体识别的加工方式并非相同，面孔加工存在特异性(Byatt，Rhodes，Michie，& Puce，2001；Campbell et al.，2001；Henke，Schweinberger，Grigo，Klos，& Sommer，1998；Itier，Latinus，& Taylor，2006)。

然而，近年来，此研究领域进一步深入，尽管实验任务仍然是采用经典的倒置范式，但研究者在实验材料的控制、被试的选择等方面对混淆变量作了进一步控制或消除，取得了许多新的成果，使面孔特异性加工理论受到了挑战。比如倒置效应陆续出现在被试识别人身体姿势的静态图片时(Reed et al.，2007；Reed，McGoldrick，Shackelford，& Fidopiastis，2004；Reed，Stone，Bozova，& Tanaka，2003；Reed，Stone，Grubb，& McGoldrick，2006；Stekelenburg & de Gelder，2004；Tao，Zeng，& Sun，2014)、识别身体姿势的运动光点图时(Troje & Westhoff，2006)(Buelthoff，Buelthoff，& Sinha，1998；Husk，Bennett，& Sekuler，2007)、养狗的专家识别狗的图片时(Diamond & Carey，1986；Robbins & McKone，2007)，以及经过专门训练的Greebles识别专家识别Greeble时(Ashworth，Vuong，Rossion，& Tarr，2008；Gauthier，Williams，Tarr，& Tanaka，1998；Gauthier & Tarr，1997；Vuong，Peissig，Harrison，& Tarr，2005)，甚至经过专门训练的被试识别房子时(Husk et al.，2007)。这些研究结果表明普通物体识别也可以像面孔识别一样达到专家识别水平(Bukach，Gauthier，& Tarr，2006；McKone，Kanwisher，& Duchaine，2007)。

亦有研究探讨面孔识别中的倒置效应是量变还是质变(Rossion，2008)。Tao等人(2014)研究发现身体姿势识别倒置效应大小存在逐渐变化。然而，以往研究并没有探讨身体加工方式是质变还是量变。因而，此研究两个实验的主要目的在于：(1)利用可能身体姿势、不可能身体姿势和碎片身体姿势作为实验材料，探讨直立状态的身体姿势与倒置状态的身体姿势识别加工成绩是否存在连续性变化，即是否可以拟合成线性关系。(2)在本实验条件下，单独抽取直立状态身体姿势和倒置状态身体姿势识别时的结果进行分析，观察在本实验条件下是否出现身体姿势识别倒置效应，以此来验证和拓展Tao等(2014)研究结果。

2 实验一

2.1 方法

2.1.1 被试

40名某大学各专业在校本科生，(男20人，女20人)，平均年龄20.6岁，所有被试均未参加过类似实验，身体健康，右利手，视力或矫正视力正常。所有参加实验的被试均获得少量报酬(10元/每人)。

2.1.2 刺激材料

实验材料同Tao等(2014)，可能身体姿势10张图片和不可能身体姿势各10张图片，在平面内每个身体姿势以30°为增幅，形成12个角度的身体姿势图片(0°，30°，60°，90°，120°，150°，180°，210°，240°，270°，300°，330°)。实验显示器为17英寸，分辨率为1024×768像素，刷新率为100Hz。图片大小400×300像素，但所有的直立状态和倒置状态的身体高度约240像素左右，形成的视角小于5°。

图1 实验一可能身体姿势和不可能身体姿势(直立条件)

2.1.3 实验设计

本实验设计采用2(刺激对：相同刺激对，不相同刺激对)×2(图片类别：可能身体姿势，不可能身体姿势)×12(旋转角度：从0°开始，以30°为增幅，12个角度)设计。实验共分4组，每组试验中，每个条件只重复一次，即48个Trials，每组内身体姿势呈现顺序和图片类别都是完全随机呈现。在每组试验中有一半相同刺激对，一半不相同刺激对。每组之间有2分钟休息。正式数据分析时，只分析相同刺激对数据，反应时取正确反应数据(去除三个标准差之外)。同时，根据身体姿势偏离直立状态的程度将将数据合并，形成2(图片类别：100%可能实现的姿势，0%可能实现的姿势)×7旋转角度(0°，30°，60°，90°，120°，150°，180°)设计。

2.1.4 实验程序

图2 实验流程图

在每一次试验中，首先呈现一个黑色“+”字注视点200ms(背景色为：RGB(140，132，127))，随后呈现第一个刺激250ms，呈现完第一个刺激后有1000ms的空屏(空屏背景颜色RGB(140，132，127))，然后，再呈现第二个刺激，第二个刺激呈现时间是直到被试反应后才消失，最后呈现等待下一次刺激呈现提示1000ms，如图2所示。如果先后呈现的的两个身体姿势完全相同，被试右手食指按小键盘中的“1”键，如果呈现的两个身体姿势不同，被试右手中指按小键盘中的“2”键。要求被试严格按照指导语进行操作，并在保证正确的前提下，尽快做出反应。程序自动记录被试的反应时和错误率。正式试验前有八次练习试验。整个试验大约需要45分钟。

2.2 实验结果

2.2.1 错误率

图3 可能身体姿势(虚线)与不可能身体姿势(实线)识别错误率与刺激对偏离直立状态角度均存在显著的线性关系

对旋转角度与错误率进行相关分析，结果发现在可能身体姿势条件条件下，旋转角度与错误率相关系数为r=0.192(p=0.001)，在不可能身体姿势条件下，旋转角度与错误率相关系数为r=0.139(p=0.020)。将各个旋转角度条件下的所有被试平均错误率与旋转角度进行线性拟合，结果发现在可能身体姿势条件下，旋转角度与错误率相关系数为r=0.888(p=0.008)。复相关系数为R2=0.789。一元线性方程显著性检验显示此线性方程达显著性水平，(F(1，5)=18.667，p=0.008)。形成的一元线性方程是y=0.000553x+0.017967，回归系数显著性检验发现回归系数达显著性水平(p=0.008)。与此同时，发现在不可能身体姿势条件下，旋转角度与错误率相关系数r=0.891(p=0.007)，复相关系数R2=0.794，一元线性方程显著性检验显示此线性方程达显著性水平，(F(1，5)=19.303，p=0.007)。形成的一元线性方程是y=0.000277x+0.033899，回归系数显著性检验发现回归系数达显著性水平(p=0.007)，如图3所示。

只抽取两个角度(0°和180°)的数据，分别对可能身体姿势条件下和不可能身体姿势条件下直立状态(0°)和倒置状态(180°)的错误率进行t检验，结果显示在可能身体姿势条件下，直立状态身体姿势识别错误率(0.0333)显著小于倒置状态身体姿势识别错误率(0.1375)，两者差异显著(t(39)=-2.712，p=0.010)。然而，在不可能身体姿势条件下，直立状态身体姿势错误率(0.0375)虽然也小于倒置状态身体姿势的错误率(0.0750)，但两者差异不显著(t(39)=-1.290，p=0.205)。

2.2.2 反应时间

图4 可能身体姿势(虚线)与不可能身体姿势(实线)识别反应与刺激对偏离直立状态角度均存在显著的线性关系

对旋转角度与反应时结果进行相关分析，结果发现在可能身体姿势条件条件下，旋转角度与错误率相关系数为r=0.159(p=0.008)，在不可能身体姿势条件下，旋转角度与反应时相关系数为r=0.072(p=0.228)。在可能身体姿势条件下旋转角度与识别反应时存在着显著的相关关系。而在不可能身体姿势识别条件下，旋转角度与识别反应时相关系数未达显著性。

将各个旋转角度条件下的所有被试平均反应时与旋转角度进行线性拟合，结果发现在可能身体姿势条件下，旋转角度与反应时的相关系数为r=0.958，对相关系数进行显著性检验，发现达到了显著性水平(p=0.001)。复相关系数为R2=0.918。一元线性方程显著性检验显示达到显著性水平，表明在可能身体姿势条件下，身体姿势旋转角度与反应时存在显著的线性关系，(F(1，5)=56.21，p=0.001)。形成的一元线性方程是y=0.612498x+602.968967，回归系数显著性检验结果达显著性水平(p=0.001)。与此同时，在不可能身体姿势条件下，旋转角度与反应时相关系数为r=0.780，对相关系数进行显著性检验，发现达到显著性水平(p=0.038)。复相关系数为R2=0.609，一元线性方程显著性检验显示结果显著，表明在不可能身体姿势条件下，身体姿势旋转角度与反应时存在显著的线性关系，(F(1，5)=7.786，p=0.038)。形成的一元线性方程是y=0.302719x+639.617134，回归系数显著性检验达显著性水平(p=0.038)，如图4所示。

只抽取两个角度(0°和180°)的数据，分别对可能身体姿势条件下和不可能身体姿势条件下直立状态身体姿势识别反应时(0°)和倒置状态身体姿势识别反应时(180°)进行t检验，结果显示：在可能身体姿势条件下，直立状态身体姿势识别反应时(592.56ms)显著小于倒置状态身体姿势识别反应时(716.74ms)，两者差异显著(t(39)=-3.496，p=0.001)。在不可能身体姿势条件下，直立状态身体姿势识别反应时(640.73)也小于倒置状态身体姿势识别反应时(745.24)，两者差异接近显著(t(39)=-1.978，p=0.055)。

2.3 讨论

实验一结果发现被试识别错误率和反应时随着身体姿势偏离标准角度的增加而逐步降低，经一元线性拟合发现两者存在显著的线性关系。从而表明在身体姿势识别加工过程中，整体布局加工是一种量上的变化。实验一还发现可能身体姿势的斜率大于不可能身体姿势斜率，而可能身体姿势的截距小于不可能身体姿势截距，不管是在错误率上还是反应时上，均表现这个趋势。截距可能反映出被试对直立状态身体姿势熟悉度高于不可能身体姿势熟悉度，斜率反映对整体布局加工破坏程度。

单独抽取可能身体姿势和不可能身体姿势0°和180°条件下的数据进行分析，在反应时上，可能身体姿势和不可能身体姿势均出现了显著的倒置效应，在错误率上可能身体姿势出现了显著的倒置效应，而不可能身体姿势没有出现显著的倒置效应。在本实验条件下，也重复出了Reed等(2003，2006)和Tao(2013，2014)的实验结果。此结果再次表明身体姿势识别与面孔识别一样，也是专家识别，整体布局加工并非特异于面孔识别，普通物体也存在着专家识别现象。

整体可能身体姿势识别不管在错误率上还是在反应时上均出现显著的倒置效应，且被试可能身体姿势的识别成绩随着身体姿势偏离标准角度的程度而呈现线性变化趋势，表现出倒置效应逐渐变小。这个结果的稳定性如何？是否依赖于整体布局加工？尚无法得知。基于此，实验二分别采用整体可能身体姿势和碎片身体姿势作为实验材料，进一步验证和拓展实验一结果。

3 实验二

3.1 方法

3.1.1 被试

14名某大学各专业在校本科生，(男2人，女12人)，平均年龄19.3岁，所有被试均未参加过类似实验，身体健康，右利手，视力或矫正视力正常。所有参加实验的被试均获得少量报酬(5元/每人)。

3.1.2 刺激材料

正式实验材料由整体可能身体姿势和碎片可能身体姿势图片各10张组成，整体身体姿势同实验一中的可能身体姿势，碎片身体姿势在整体可能身体姿势上制作，同Tao(2014)研究中碎片身体姿势，见图5。

3.1.3 实验设计

本实验设计采用2(刺激对：相同刺激对，不相同刺激对)×2(图片类型：整体身体姿势，碎片身体姿势)×12(旋转角度：从0°开始，以30°为增加步调)设计。实验共分3组，每组试验中，每个条件只重复两次，即96个Trials，每组内，相同刺激对和不同刺激对、整体身体姿势和碎片身体姿势，身体姿势呈现角度都完全随机。每组之间有2分钟休息。正式试验前12次练习。整个实验约需35分钟。正式数据分析时，只分析相同刺激对数据，取正确反应反应时数据(去除三个标准差之外的数据)。

3.1.4 实验程序

同实验一

3.2 实验结果

3.2.1 错误率

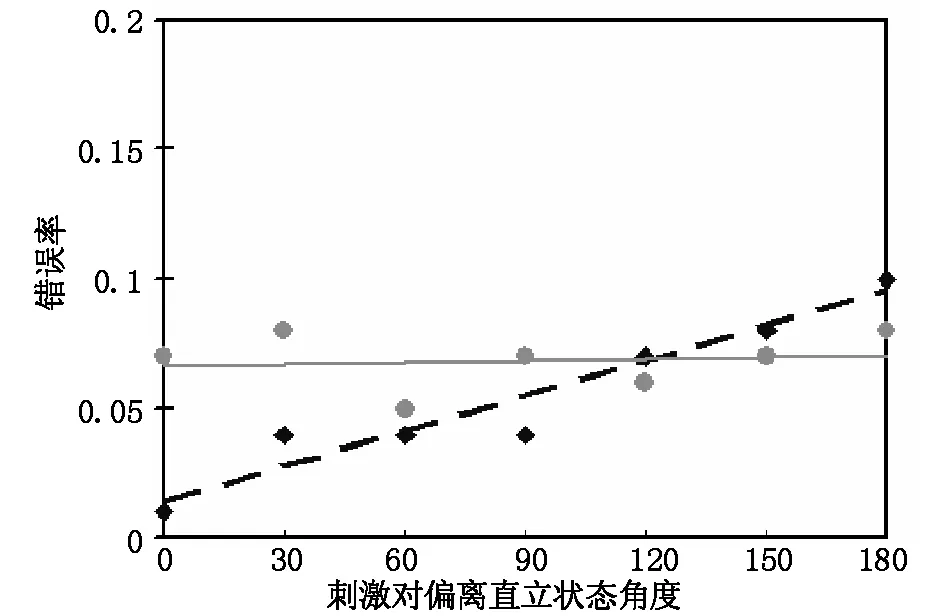
图6 整体身体姿势(虚线)识别错误率与刺激对偏离直立状态角度存在显著的线性关系，而碎片身体姿势识别错误率(实线)与刺激对偏离直立状态角度却不存在显著的线性关系

对旋转角度与错误率结果进行相关分析，结果发现在整体身体姿势识别条件下，旋转角度与错误率的相关系数为r=0.323(p=0.001)，旋转角度与识别错误率存在着显著的相关关系。而在碎片身体姿势识别条件下，旋转角度与错误率相关系数为r=0.015(p=0.887)，旋转角度与识别错误率不存在着显著的相关关系。

将各个旋转角度条件下的所有被试平均错误率与旋转角度进行线性拟合，结果发现在整体身体姿势条件下，旋转角度与错误率相关系数为r=0.96，对相关系数进行显著性检验，发现达到显著性水平(p=0.001)，复相关系数为R2=0.922。一元线性方程显著性检验结果达到显著性水平，表明在整体身体姿势条件下，身体姿势旋转角度与错误率存在显著的线性关系，(F(1，5)=59.321，p=0.001)。形成的一元线性方程是y=0.000439x+ 014881，回归系数检验达显著性水平(p=0.001)。与此同时，发现在碎片身体姿势识别条件下，旋转角度与错误率相关系数r=0.135，对相关系数进行显著性检验，发现未达到显著性水平(p=0.773)，复相关系数R2=0.018，一元线性方程显著性检验结果显示未达到显著性水平，表明在碎片身体姿势识别条件下，身体姿势旋转角度与错误率不存在显著的线性关系，(F(1，5)=0.092p=0.773)。如图6所示。

只抽取两个角度(0°和180°)的数据，分别对整体身体姿势条件下和碎片身体姿势条件下直立状态(0°)和倒置状态(180°)的错误率进行t检验，结果显示在整体身体姿势条件下，直立状态整体身体姿势识别错误率(0.012)小于倒置状态整体身体姿势识别错误率(0.095)，两者差异接近显著(t(13)=-1.989，p=0.068)。然而，在碎片身体姿势条件下，直立状态身体姿势错误率(0.0714)小于倒置状态身体姿势的错误率(0.0833)，但两者差异不显著(t(13)=-0.249，p=0.907)。

3.2.2 反应时间

图7 识别整体身体姿势(虚线)的反应时与刺激对偏离直立状态的角度存在显著的线性关系，而识别碎片身体姿势(实线)的反应时与刺激对偏离直立状态的角度却不存在显著的线性关系

对旋转角度与反应时结果进行相关分析，结果发现在整体身体姿势识别条件下，旋转角度与反应时相关系数为r=0.236(p=0.019)，旋转角度与识别反应时存在着显著的相关关系。在碎片身体姿势识别条件下，旋转角度与反应时相关系数为r=0.026(p=0.803)。旋转角度与识别反应时不存在显著的相关关系。

将各个旋转角度条件下的所有被试平均反应时与旋转角度进行线性拟合，结果发现在整体身体姿势条件下，旋转角度与反应时的相关系数为r=0.863，对相关系数进行显著性检验，发现达到显著性水平(p=0.012)，复相关系数为R2=0.745。一元线性方程显著性检验结果达到显著性水平，表明在整体身体姿势条件下，身体姿势旋转角度与反应时存在显著的线性关系，(F(1，5)=14.605，p=0.012)。形成的一元线性方程是y=0.792x+ 729.858，回归系数检验达极其显著性水平(p<0.001)。与此同时，发现在碎片身体姿势条件下，旋转角度与错误率相关系数r=0.268，对相关系数进行显著性检验，发现未达显著性水平(p=0.562)，复相关系数R2=0.072，一元线性方程显著性检验结果显示未达到显著性水平，表明在碎片身体姿势识别条件下，身体姿势旋转角度与反应时不存在显著的线性关系，(F(1，5)=0.386p=0.562)。如图7所示。

只抽取两个角度(0°和180°)的数据，分别对整体身体姿势条件下和碎片身体姿势条件下直立状态身体姿势识别反应时(0°)和倒置状态身体姿势识别反应时(180°)进行t检验，结果显示：在整体身体姿势条件下，直立状态整体身体姿势识别反应时(699.98ms)显著小于倒置状态整体身体姿势识别反应时(838.11ms)，两者差异显著(t(13)=-3.900，p=0.002)。在碎片身体姿势条件下，直立状态碎片身体姿势识别反应时(823.39)也小于倒置状态碎片身体姿势识别反应时(844.38)，两者差异未达显著性水平(t(13)=-0.386，p=0.706)。

3.3 讨论

实验二整体身体姿势识别重复出了实验一的结果，再次支持了身体姿势识别加工过程中，倒置效应是一种量上的变化。不仅如此，在碎片身体姿势识别条件下，结果并没有发现被试的识别成绩随着先后呈现的两个身体姿势刺激对偏离直立状态(标准角度)程度的增加而逐渐降低。这个结果表明被试身体姿势识别成绩随着身体姿势偏离直立状态(标准角度)程度的增加而逐渐降低的趋势依赖于整体布局加工。

单独抽取整体身体姿势和和碎片身体姿势中的0°条件和180°条件的成绩进行分析。在反应时和错误率上，整体身体姿势识别均出现了显著的倒置效应。此结果与以往身体姿势识别研究的结果一致(Bosbach，Knoblich，Reed，Cole，& Prinz，2006；Reed，Stone，Bozova，& Tanaka，2003；Stekelenburg & de Gelder，2004；Tao & Sun，2013；Tao，Zeng，& Sun，2014；Yovel，Pelc，& Lubetzky，2010)。然而，碎片身体姿势识别，不管是在反应时上还是在错误率上，均未出现显著的倒置效应。从而表明，被试对整体身体姿势的识别是采用整体布局的加工方式，然而在碎片身体姿势识别条件下，被试采用特征侦察方式完成任务。

4 总讨论

此研究主要探讨面孔的类似物即身体姿势的识别，所产生出的倒置效应是否存在量的延续。此研究两个实验结果一致发现：整体可能身体姿势与整体不可能身体姿势的识别，其旋转角度与识别成绩之间存在显著的相关关系，均可拟合成线性关系，表现出随着身体姿势偏离直立状态角度的增加，被试识别成绩呈现逐渐下降的趋势，此结果支持了身体姿势识别倒置效应是量的延续。实验二发现碎片身体姿势识别时则不存在随着碎片姿势偏离直立状态角度的增加，被试识别成绩呈现逐渐下降的趋势，也不存在倒置效应，从而表明身体姿势识别的倒置效应在量的延续上依赖于整体布局加工。这个结果得到了面孔识别领域研究结果支持，如Sekuler等(2004)研究发现倒置操作后，面孔再认加工并非是性质上的改变，仅仅是加工方式在量上的变化，即使面孔倒置后，面孔识别也有整体布局加工成分的参与。这说明倒置操纵后，两种加工方式并非完全对立，而是依据的主要信息不同，辨别时所赋予的权重也不同(Sekuler et al.，2004)。

两个实验分别抽取了可能身体姿势和不可能身体姿势中的两个条件，即0°(直立状态)和180°(倒置状态)进行分析。结果发现可能身体姿势和不可能身体姿势识别均存在倒置效应。此结果中可能身体姿势识别倒置效应与Reed等(2003，2006)的研究结果相一致。从而表明身体姿势识别是整体布局加工。其产生的原因是身体姿势本身的层次性(Structural hierarchy of body parts)。并且身体姿势识别中的倒置效应主要由组成身体姿势的各元素之间的相对位置信息和身体姿势模板这两类信息所引起(Reed et al.，2006；Yovel et al.，2010)。实验二的结果也支持此结论。在实验二中，碎片身体姿势识别不存在倒置效应。此结果与Tao等(2014)研究结果一致。这是由于在碎片身体姿势中，四肢的位置关系被打乱，因而被试无法利用整体信息和四肢的相对位置信息，因此只能采用部分加工方式完成实验任务，从而在结果中表现出碎片身体姿势的识别未出现倒置效应。

在物体识别研究领域，多数研究者将重点放在物体识别加工方式的对立上，而没有从一个整体的角度来研究物体识别的加工方式。即过去的研究只比较直立状态与倒置状态，从而得出面孔识别倒置效应是质的变化这一结论。但是直立状态与倒置状态是两个极端值，没有从连续的角度来进行研究。Rossion(2008)研究发现，在面孔识别中，面孔偏离直立状态的角度与识别成绩之间存在线性关系，从而表明面孔识别的倒置效应并非质的变化。此研究利用面孔物体的类似物身体姿势作为实验材料进行研究，其结果支持物体识别倒置效应应是量的延续，并非质的飞跃这一结论。

然而，这个研究结果仅从行为学层次上揭示了身体姿势识别中倒置效应是量的延续，目前从脑成像角度直接比较身体姿势倒置效应与面孔倒置效应较少，未来可就此作进一步研究。此外，此研究只操纵了12个角度，未来研究可进一步系统操纵更多角度来继续探讨物体识别倒置效应是量变还是质变。

5 结论

以偏离直立状态角度为变量，对总平均数据进行线性拟合，结果发现整体可能身体姿势识别与不可能身体姿势识别均出现了显著的线性关系，然而，碎片身体姿势识别却没有出现此现象。此结果表明身体姿势识别中倒置效应是量的延续，并且这种量的延续依赖于整体布局加工。单独抽取0°(直立状态身体姿势)和180°(倒置状态身体姿势)的数据进行分析，生理机制上可能的身体姿势和生理机制上不可能的身体姿势均出现了显著的倒置效应，而碎片身体姿势却没有出现倒置效应。