一种基于SCAD的改进谓词发现方法

郑晓东, 潘敬敏, 胡汉辉

(1. 东南大学 经济管理学院, 江苏 南京 211189; 2. 东南大学-蒙纳士大学苏州联合研究生院, 江苏 苏州 215000)

归纳逻辑编程(inductive logic programming, ILP)[1]是机器学习与逻辑程序设计相结合形成的新研究领域,为知识工程等工智能领域提供了新技术,是机器学习的前沿研究课题.但ILP是在受限制的一阶逻辑框架中进行归纳推理,因此面临的难题是在给定词汇不足的情况下如何扩展假设语言.

解决该问题的方法是通过引入新的谓词使其与给定的词汇在逻辑形式上相适应,即谓词发现 (predicate invention, PI).谓词发现方法可分为基于ILP和基于统计学习2类.然而,它们存在共同的致命缺点,即如果程序在执行的过程中使用了一个表达不当的新谓词,则在后续谓词发现的过程中可能会导致错误级联.

为解决此问题,WANG W.Y.等[2]提出了基于结构化稀疏的软谓词发现方法,通过将集合的参数一起正则化的方式减少要学习参数的数量,可有效去除具有“噪声”的谓词以使得谓词发现的鲁棒性增强.

然而,由于谓词及其领属结构信息的复杂性,导致谓词会产生较大歧义[3].笔者发现软谓词发现方法有如下不足: ① 没有尝试将更多的正则化稀疏模型引入到谓词发现系统中; ② 考虑了有偏稀疏模型但没有考虑无偏稀疏模型对谓词发现的影响.

文中提出一种基于平滑削边绝对偏离(smoothly clipped absolute deviation, SCAD)的正则化稀疏的改进谓词发现方法.该方法在正则化稀疏的谓词发现方法的基础上,通过引入SCAD正则化稀疏模型优化算法的性能.文中主要工作分为以下2个方面:一是在软谓词发现中引入SCAD这一正则化稀疏模型,二是针对无偏稀疏性,着重观察SCAD对软谓词发现结果的影响.

1 基于正则化稀疏的软谓词发现

1.1 软谓词发现

传统的谓词发现方法通常是压缩一组紧密相关的规则发现新的谓词.但传统谓词发现方法的缺点是在输入有噪音的数据时,谓词发现的中间过程可能因为选择表达不当的子句导致错误级联.为了解决这一难题,WANG W.Y.等[4]提出基于结构化稀疏的软谓词发现方法,它在程序执行的过程中并不创建新的谓词符号,而是将相似的概念组合在一起,并利用基于结构化稀疏的技术来探索密切相关的概念和规则.这一方法对谓词发现方法研究的进展起了重大作用.刘洁群[5]提出一种基于谓词推理的冲突检测算法,该算法通过谓词表达策略的触发条件和作用效果,并通过推理自动化地获得策略之间的冲突关系.

目前谓词发现方法的研究主要分为2类:基于ILP的谓词发现方法[6]和基于统计学习的谓词发现方法[7].在这2个类别的基础上又演变出一系列其他的谓词发现方法,如矩阵排序的谓词发现方法[8].

1.2 元素正则化

文中选择一阶概率语言ProPPR这一逻辑平台进行谓词发现,适合间接查询的ProPPR的默认正则项针对稀疏估计有较好的处理性能,但对于噪音估计可能不太理想,因为错误的一阶逻辑程序可能导致下游应用中出现更多的错误.此时引入元素正则化技术,定义一个权重参数向量ω,根据使用一阶逻辑参数学习的结构学习的研究,ω中每个权重元素对应于一阶逻辑子句候选项.采用Lasso公式,其目标函数为

min(-η+μ||ω||1),

(1)

式中:η为误差项;μ≥0为可调参数.与岭估计不同,即使目标函数是不可微的,上述Lasso惩罚项也将产生稀疏估计.为优化上述目标函数,可使用近似运算符,每个权重分量ω通过收缩值σ而趋向于0,表达式为

signum(ω)max(0, |ω|-σ).

(2)

延迟L1正则化更新为

(3)

式中:σ为累积正则化更新的总数;β为学习率.

文中使用延迟L1更新算法进行优化.主要思想如下:对每个示例中的所有特征进行正则化更新速度很慢且几无必要,故可先缓存相关功能的正则化更新,然后再更新这些累积的正则化之变化.

1.3 结构化图拉普拉斯正则化

一个与PI相关的挑战是,因为重复使用发现的谓词使得它们难以通过简单的元素正则化从矩阵中去除.为更好地包含每个逻辑子句特征之间的依赖关系,文中使用了一个成对图拉普拉斯(pair-wise graph Laplacian)惩罚项,表达式为

min(η+ζ∑(p,q)||ωp-ωq||A(p,q)),

(4)

式中:ζ为控制结构化补偿强度的正则化系数;A(p,q)为逻辑子句之间成对相似性的相邻矩阵,基本思想是通过学习后给相似的逻辑子句赋予相似的权重.比如下面的子句:

brother(X,Y):-son(X,Z),father(Z,Y).

brother(X,Y):-son(X,Z),mother(Z,Y).

由于它们具有相同的目标并且RHS的第1谓词也相同,因此给予2者相似的权重是有意义的.为构造稀疏矩阵A,使用类似CHAMP风格的分析方式[9]:对于所有具有相同目标并且|RHS|=1的子句对,在邻接图中连接它们;对于所有具有相同目标并且|RHS|=2的子句对,如果右手侧的第1个谓词相同,就在A中将这2个子句也连接在一起.例如,并不需要为第2个子句创建1个新的实谓词,而是直接在关联矩阵A中为这1对规则赋予权重值为1即可.

为实现这种方法,使用一个度矩阵D表示矩阵A中每个条目的连接总数,并且将图形拉普拉斯定义为L=D-A,其将优化公式转换为

min(-η+ζwTLw),

(5)

式中η为损失.像岭回归一样,这个正则化矩阵是一个L2惩罚项.

1.4 通过组Lasso的正则化稀疏

当拉普拉斯正则化给相似的子句组赋予相似的权重值时,它通常不会通过将不正确的相关子句组的权重值置0来达到移除它们的目的,这是拉普拉斯正则化的问题.为解决这个问题,可使用组Lasso的稀疏正则化(regularized sparsity via group Lasso)[10-11]:

(6)

式中:L为特征组的总数;ωl为第l组的参数向量.通过公式(6)的运用,即可将问题转换成一个正则化稀疏的学习问题.

1.5 通过弹性网的正则化稀疏

组Lasso正则化稀疏的问题是在矩阵A选择具有关联关系的特征组时并不能实现自动组效应,这在一定程度上影响了软谓词发现的执行速度.可通过朴素弹性网[12]解决这个问题:

(7)

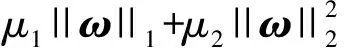
1.6 通过SCAD的正则化稀疏

弹性网在特征选择的过程中实现了自动组效应,但弹性网并不是无偏稀疏模型,所以文中尝试引用SCAD惩罚这一正则化稀疏模型.SCAD[13]模型是一种近似无偏稀疏模型:

(8)

式中:l∈{1,2,…,L};φρ,γ(·)为SCAD惩罚项,惩罚项中ρ≥0,γ>2.SCAD模型对绝对值小于ρ的回归系数(即噪声变量的回归系数)的压缩作用与Lasso相同,倾向于将这一部分回归系数压缩为0.对绝对值位于区间[ρ,ργ]内的回归系数(即目标变量的回归系数),随着回归系数绝对值的增大而减小压缩的程度.对于绝对值大于ργ的回归系数,不再对其进行压缩.由于减小甚至避免了对目标变量对应回归系数的压缩,所以SCAD模型克服了Lasso有偏估计的缺点,改善了其参数估计一致性和变量选择一致性.

2 试 验

2.1 试验数据集

使用欧洲皇室家庭关系数据集[13]作为试验数据集,可更好衡量基于SCAD的软谓词发现方法的性能.超过30 kB数据信息的家庭数据集包含3 010个个体和1 422个欧洲皇室家庭.

2.2 试验目标

试验目标是在一阶逻辑平台ProPPR上引入SCAD正则化稀疏算子后进行谓词发现时,通过与引入弹性网正则化稀疏算子、组Lasso正则化稀疏算子、拉普拉斯正则化稀疏算子等正则项互相比较证明文中所提方法能够提高谓词发现的平均精准度并能减少对知识库进行查询的时间.同时,通过考察知识库的完善程度来比较基于不同正则化稀疏算子谓词发现方法的试验性能.

2.3 试验方法

确定完试验数据集后,对家庭关系数据集按时间分割成训练集和测试集2部分,分别包括21 430,8 899个事实.在下文的知识库完善试验中,随机删除训练集和测试集中各自50%的事实数据,并用软谓词发现方法完善缺失的事实数据.

试验采用平均准确率(mean average precision, 用θMAP表示)来衡量谓词发现的准确度.θMAP已经在很多任务中展示出它的鲁棒性和稳定性,并且已被广泛地应用到关系学习的任务中[12,14-15],也可评估文中方法的有效性.每个试验重复3次,并记录试验结果的平均值;同时比较了基于不同正则算子在测试集上进行推理的时间.

2.4 试验与分析

本小节主要针对2.1节提到的家庭关系数据集,使用2.3节提出的试验方法进行一系列试验.基于5种不同的正则化稀疏算子即元素正则化稀疏算子、结构化图拉普拉斯正则化稀疏算子、组Lasso正则化稀疏算子、弹性网正则化稀疏算子和SCAD正则化稀疏算子进行试验.根据试验结果,比较不同的正则化稀疏算子对软谓词发现性能的影响.

2.4.1μ值选择

μ作为正则化稀疏算子的系数,其取值直接影响到知识库完善试验的性能,因此应先确定μ的最优值.图1显示了正则化算子不同时,正则化系数μ与θMAP的关系.

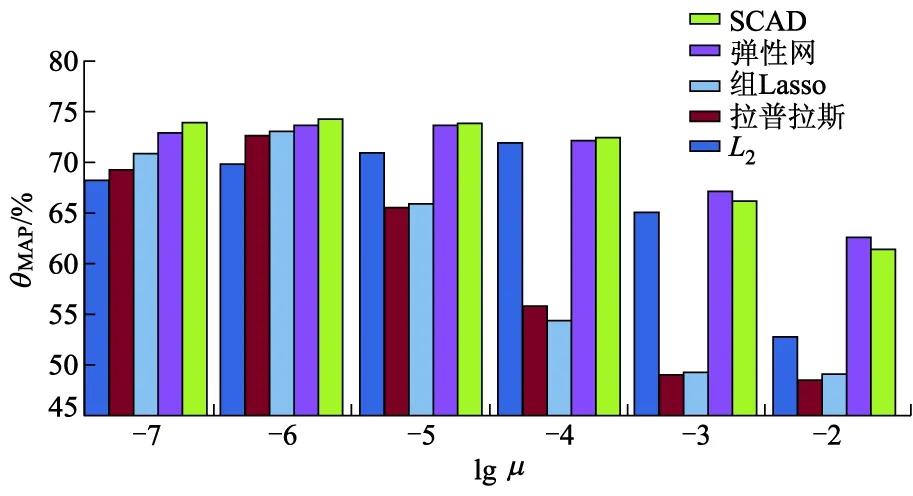
图1 正则化系数μ与θMAP的关系

由图1可见,随着μ值的增加,θMAP的值经历了先增加后减少的变化趋势.但当L1惩罚项的正则化系数μ1取值为0.000 001时,当L2惩罚项的正则化系数μ2取值为0. 000 1时,θMAP的取值达到峰值.这2个值将贯穿整个试验过程.图2显示了正则化算子不同时,正则化系数μ与知识库完善所需推理时间t的关系.

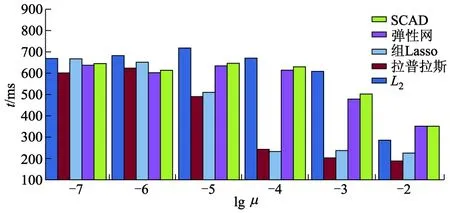
图2 正则化系数μ与知识库完善所需推理时间的关系

由图2可见,在其他变量相同时,SCAD方法推理时间随着正则化系数μ的增加而减少,且SCAD方法的推理时间与其他方法无明显差异.

2.4.2α值选择

α作为ProPPR中排序算法PageRank-Nibble中的1个参数,其取值的大小直接影响到知识库完善试验的性能,所以应先通过试验确定α的最优值.

图3中显示了正则化算子不同时,正则化系数α与θMAP的关系.

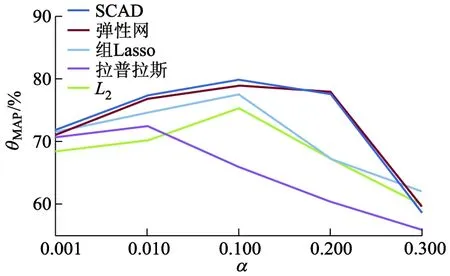
图3 正则化系数α与θMAP的关系

由图3可见,当α=0.100时,元素正则化稀疏算子、组Lasso正则化稀疏算子、弹性网正则化稀疏算子和SCAD正则化稀疏算子的θMAP值达到峰值.图4显示了正则化算子不同时,正则化系数α与知识库完善所需推理时间t的关系.试验表明,α=0.100是最优值.

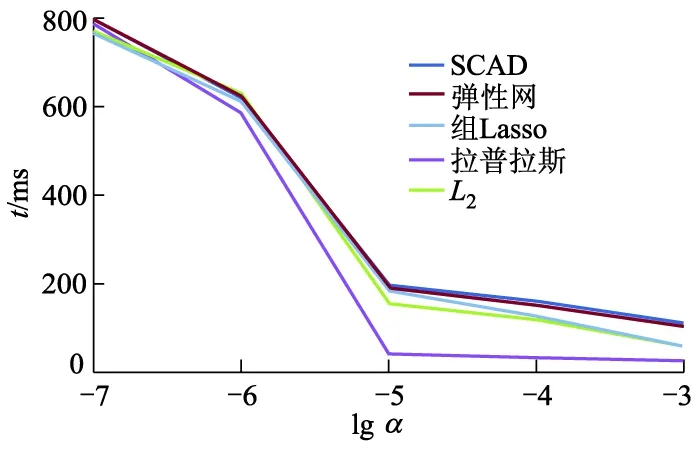
图4 正则化系数α与知识库完善所需推理时间的关系

2.4.3 知识库完善试验

通过第2.4.1小节和第2.4.2小节确定μ和α的最优值后,本小节基于5种不同正则化稀疏算子(元素正则化稀疏算子、结构化图拉普拉斯正则化稀疏算子、组Lasso正则化稀疏算子、弹性网正则化稀疏算子和SCAD正则化稀疏算子)进行知识库完善的试验.从家庭关系数据集中抽取6对关系进行了试验,表1给出了不同正则化方法的θMAP结果.

由表1可见,对于软谓词发现来讲,基于SCAD正则化稀疏的软谓词发现方法在知识库完善的试验中有较好的测试性能,它远超过传统的基于岭回归基线(即基于元素正则化稀疏算子的软谓词发现方法)的性能,它的θMAP平均值为0.755;而基于SCAD正则化稀疏算子的软谓词发现方法的θMAP平均值达到0.798.总的来说,文中结果与先前研究中稀疏性导致正则化项经验损失最小的结果一致[13]:具有较少非0权重的紧致参数空间可能产生更好的结果.

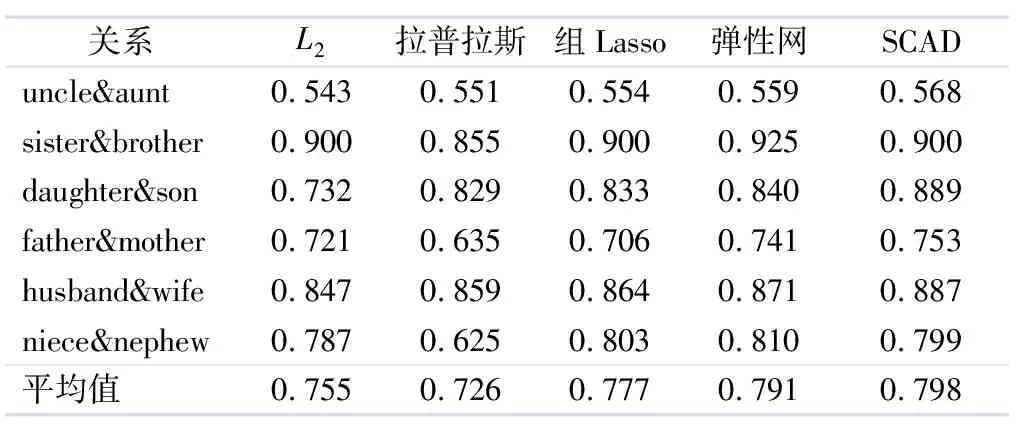
表1 不同正则化方法的θMAP结果

将文中提出的方法应用于家庭关系数据集,在5种不同正则化稀疏算子的情况下,家庭关系数据集中推理6对关系所需推理时间的比较见表2.

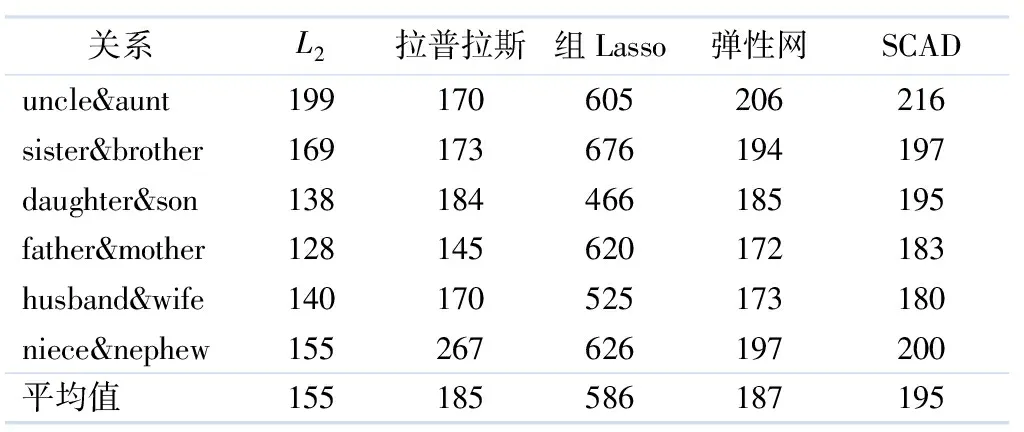
表2 各方法抽取关系的平均时间比较 ms

由表2可见,在相同变量情况下,SCAD抽取关系的平均时间优于组Lasso方法,略低于L2、弹性网和拉普拉斯方法.

2.4.4 试验结果

将以上试验结果总结如下:

1) 将L1惩罚项的正则化系数μ1的值设置为0.000 001,将L2惩罚项的正则化系数μ2的值设置为0.000 1,将参数α的值设置为0.100时,基于正则化稀疏的软谓词发现方法的试验性能最优.

2) 从θMAP的平均值来讲,文中提出的基于SCAD正则化稀疏算子的软谓词发现方法的性能比基于其他正则化项的软谓词发现方法的性能更优.从知识库完善所需推理时间的结果来看,文中提出的基于SCAD的软谓词发现方法也具有一定优势.

3 结 论

1) 文中使用基于SCAD正则化算子和CHAMP方式压缩再诱导重叠组的方法,克服传统谓词发现方法的不足及提高软谓词发现方法的性能.

2) 在超过30 kB数据信息的皇室家庭数据集上进行试验,试验表明基于SCAD正则化算子的软谓词发现方法比基于组Lasso的谓词发现方法和基于弹性网的谓词发现方法具有更好的性能,其预测结果的平均精度值达到0.798,远远超过基于拉普拉斯正则化的软谓词发现方法的0.726.

3) 在未来工作中,可尝试将更多的正则化稀疏方法引入到试验中以选择出更优的方案.