半挂汽车列车AFS/DYC集成控制策略设计及验证

马玉喆, 张祖锋, 牛宗元, 丁能根

(1. 北京航空航天大学 交通科学与工程学院, 北京 100191; 2. 空军预警学院, 湖北 武汉 430345)

由于半挂汽车列车铰接和多轴结构、满载质心较高等特性使其操纵性和行驶稳定性都较差,其安全性已经成为制约道路交通运输事业发展的瓶颈.

从早期的制动防抱死系统(anti-lock brake system,ABS)[1],到车身电子稳定程序(electronic stability program,ESP)[2],汽车的行驶稳定性可以通过底盘稳定性控制系统得到改善.直接横摆力矩控制(direct yaw-moment control,DYC)是ABS功能的延伸;主动前轮转向系统(active front steering,AFS)对前轮小角度操作改变汽车横向受力,完成对横摆运动的控制,提高汽车行驶安全性.AFS性能在车辆线性操作区域内才会发挥出来,DYC在线性和非线性区域内都有良好的性能,但持续的横摆力矩控制会影响驾驶员驾驶和乘员乘坐舒适性[3],将2种方法结合是提高车辆操纵稳定性的常用方法[4],多以质心侧偏角和横摆角速度的理想响应作为参考进行控制策略的设计[5].半挂汽车列车质量大、重心高,常见的失稳形式有侧滑、折叠等.文献[6]通过监测半挂车相对于牵引车的转角(即折叠角或折腰角)来判断是否有折叠危险.文献[7]理论上说明了用状态观测器预测和估计折叠角的可行性.文献[8]采用主动前轮转向或类似的方法来抑制车辆折叠.

笔者采用滑模控制、模糊控制方法,以追踪期望的横摆角速度、折腰角为目标,基于简化的3自由度线性单轨模型设计半挂汽车列车的AFS/DYC集成控制策略,并以TruckSim中的高精度车辆模型作为试验车辆,在TruckSim与Simulink的联合仿真中对控制策略进行验证.

1 参考模型

1.1 3自由度车辆模型的建立

选择6轴半挂汽车列车为目标控制车型,基于TruckSim建立该车型的仿真模型.采用简化模型即线性3自由度单轨汽车列车模型作为计算横摆角速度的参考模型[9-10],如图1所示.牵引车的前轴即3自由度模型中的轴1,后两联轴合并为轴2,半挂车的后三联轴合并为轴3.

模型简化过程中作如下假定:轮胎采取线性模型(即轮胎侧偏刚度为常数),不考虑牵引车与半挂车的纵向耦合作用,不考虑牵引车与半挂车的纵向速度差异,对各轮胎的侧偏角采用小角度假设.

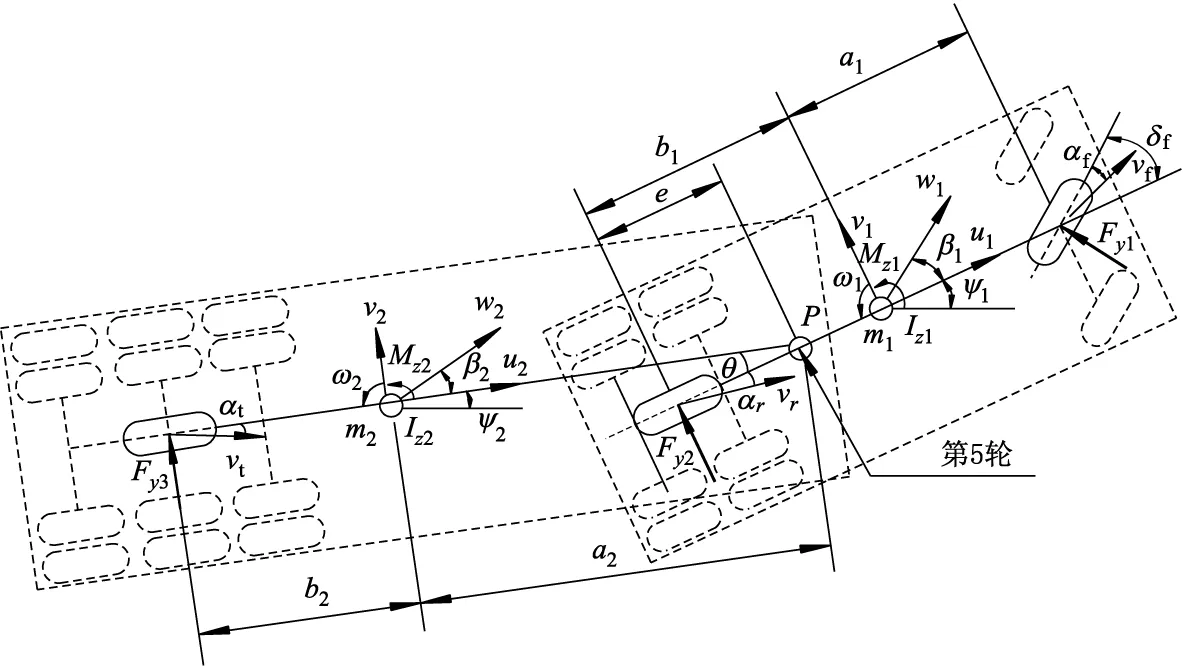
图1 线性3自由度单轨汽车列车模型

利用拉格朗日方法,施加AFS/DYC集成控制的半挂汽车列车3自由度线性单轨模型的动力学方程为

(1)

式中:m1,m2分别为牵引车和半挂车质量;u为两者的纵向速度,速度相等;v1,v2分别为两者的横向速度,且有v1=uβ1,v2=uβ2,β1,β2分别为两者质心侧偏角;ω1,ω2分别为两者横摆角速度;Fy1,Fy2,Fy3为3轴轮胎侧向力;Fpy为第5轮处牵引车与半挂车的侧向相互作用力;Iz1,Iz2分别为两者横摆转动惯量;a1,b1分别为牵引车质心到前、后轴距离;a2,b2分别为半挂车质心到第5轮和其后轴距离;e为牵引车后轴到第5轮的距离;Mz1,Mz2分别为牵引车与半挂车所需附加横摆力矩;θ为牵引车与半挂车的相对转角(称为折腰角);δ为牵引车前轮转角,在控制算法中,以δd和δc来区分驾驶员转向盘转角输入确定的前轮转角和AFS施加的附加前轮转角.

轮胎的侧向力与侧偏角认为是线性关系:

(2)

式中:Cf,Cr,Ct分别为3自由度模型中1,2,3轴的线性侧偏刚度;αf,αr,αt分别为模型中1,2,3轴的侧偏角.

各轮胎侧偏角的计算方法如下:

(3)

式中L2为半挂车后轴到第5轮的距离.

铰接点处的运动约束方程为

(4)

根据式(1) - (4)化简得到系统的状态方程为

(5)

d=b1-e+a2,d1=b1-e;

σ=Cf+Cr+Ct,ρ=-Cfa1+Crb1+Ctd1,

1.2 参考量的确定

1.2.1 参考横摆角速度

当系统达到稳态时,各状态量的导数值为0,因此得到稳态下的状态方程:

(6)

由克莱姆法则得到对应于前轮转角的稳态横摆角速度为

(7)

1.2.2 参考折腰角

参考折腰角主要受路面附着系数、纵向速度和前轮转角3个因素影响.通过3自由度分叉分析[11],得到给定工况下稳定平衡点的折腰角大小,并将其作为参考折腰角.μ=0.3时,所得部分结果数据如表1所示.仿真中参考折腰角均通过3维查表线性插值得到.

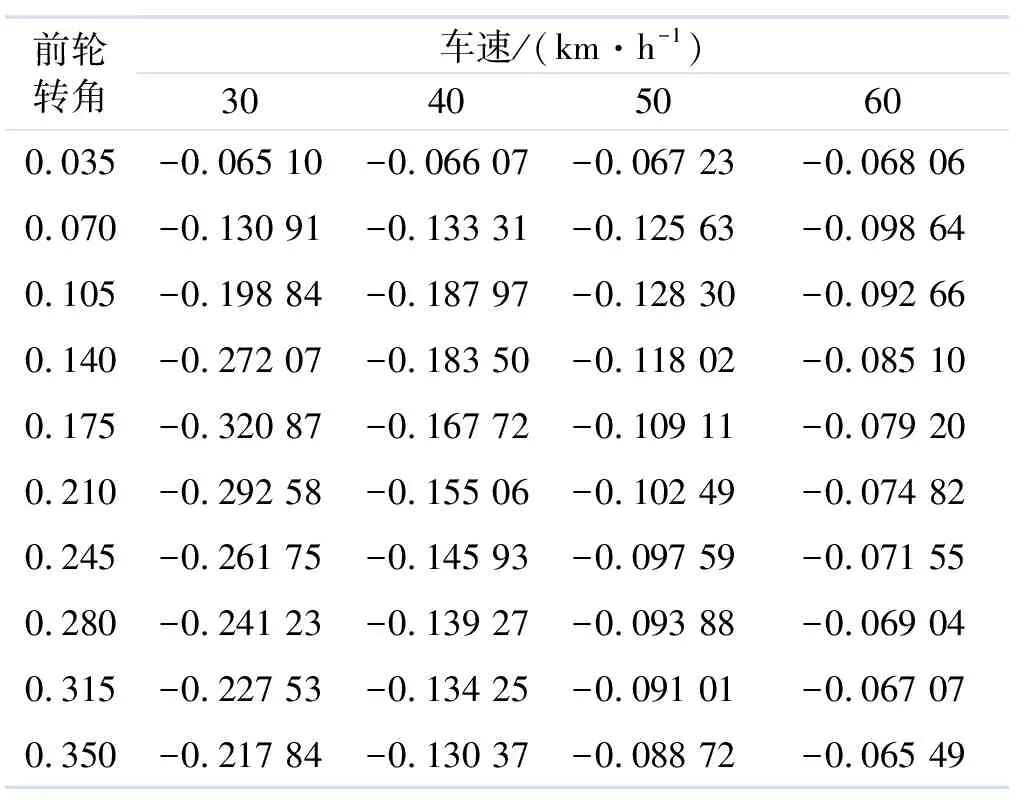
表1 参考折腰角查表 rad

2 控制系统设计

以追踪牵引车横摆角速度与折腰角为目标设计控制策略,控制系统分为顶层横摆力矩控制器、中层模糊控制器和底层制动力矩分配器3部分.

2.1 顶层横摆力矩控制器

采用滑模控制,将实际牵引车横摆响应、折腰角与各自参考响应偏差作为控制器输入,从而得到施加到牵引车和半挂车上的横摆力矩.滑模函数为

(8)

式中:S1,S2分别为横摆角速度偏差与折腰角偏差;θd为参考折腰角.

为使控制律连续,采用反正切趋近方式:

(9)

式中k1,k2为比例因子.

将式(1)-(4)代入式(9)可得

(10)

由此得

例如上海旅游高等专科学校、南京旅游职业学院、山东旅游职业学院等六所旅游类高职院校成立的“中国旅游院校五星联盟”(CTI5)，加强了成员院校之间协同合作，促进旅游信息资源的共建共享。2010年，CTI5在CALIS支持下构建了中国旅游院校五星联盟CALIS共享域服务中心平台，该平台是以旅游学科为特色、跨地区的文献信息服务平台，在成员院校中资源建设、资源共享、信息服务、人才培养等方面起到积极的推动作用，为联盟外其他高职院校的跨地区信息资源共建共享起到了一定的示范和先导作用。同时平台也面向社会提供服务，使特色资源服务于社会，提升了联盟高校的社会影响力。[5]

(11)

(12)

由于半挂车后轴垂直载荷较低,在较低附着系数时易因制动导致轮胎力饱和,故在式(12)中加入比例因子k3,即

(13)

比例因子k1,k2,k3由试凑法确定,在不同附着系数下的最佳取值不同,部分取值如表2所示.

2.2 模糊控制器

AFS/DYC集成控制策略表示如下:

(14)

式中k介于0～1之间,表示牵引车所需附加横摆力矩中分配给直接横摆力矩控制实现的成分多少.

AFS所需的前轮附加转角为

(15)

通过式(13)可得

(16)

控制器隶属函数描述如图2所示,其中，N,Z,P分别表示负值、0、正值;S,M,B分别表示小值、中值、大值.模糊控制规则如表3所示.

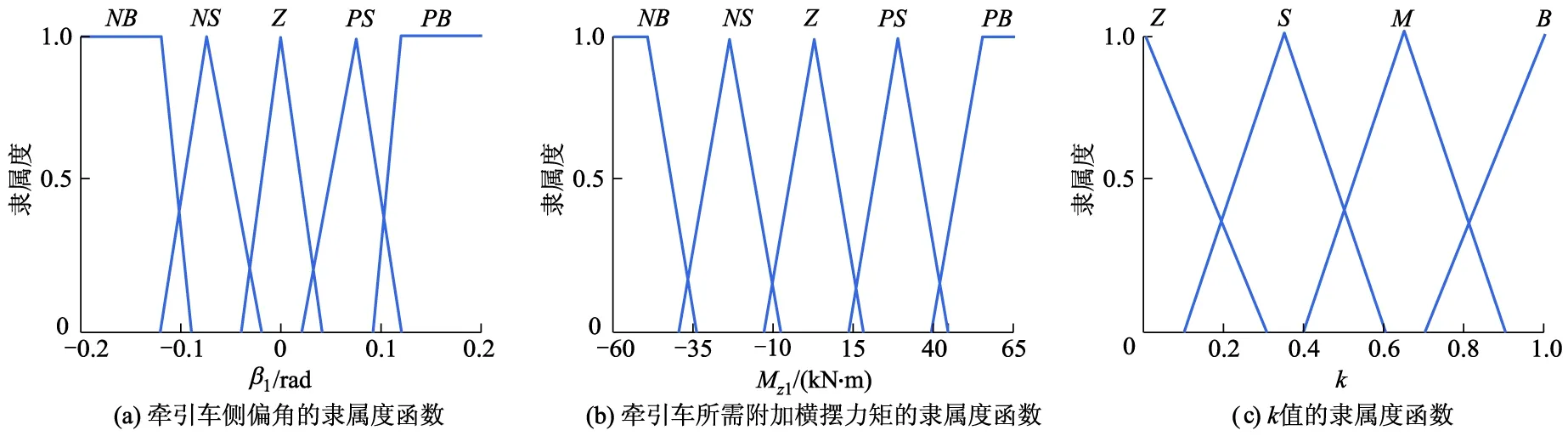
图2 模糊控制的隶属度函数

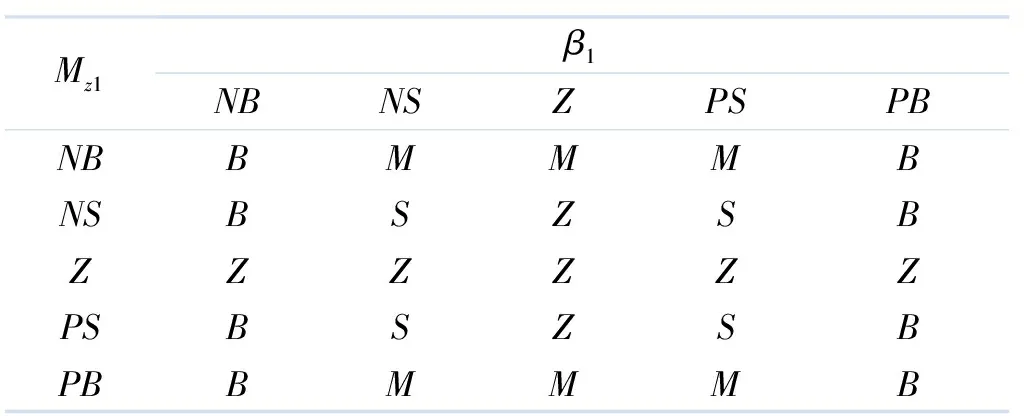
Mz1β1NBNSZPSPBNBBMMMBNSBSZSBZZZZZZPSBSZSBPBBMMMB

2.3 制动力控制器

目标制动车轮及其制动力矩由制动力分配器决定,多联轴同侧各车轮制动力平均分配.制动力矩为

(17)

在仿真过程中,3自由度模型中的轴2与轴3由多个轴组成,所需的制动力矩被这组轴平均分配并实现横摆力矩控制.

目标车轮的选择根据牵引车与半挂车的实际横摆响应与参考横摆响应的对比确定.为保证整车的横向稳定性且简化控制算法,半挂车在转向相对不足时不施加直接横摆力矩控制.

最终确定的制动力矩分配规则如表4,5所示, 1,2,3/5,4/6分别为牵引车的左前轮、右前轮、左后轮和右后轮;7/9/11,8/10/12分别为半挂车的左轮和右轮.

表4 牵引车制动目标轮胎确定规则

表5 半挂车制动目标轮胎确定规则

3 仿真分析

3.1 TruckSim-Simulink联合仿真

仿真所用双移线路径如图3所示.

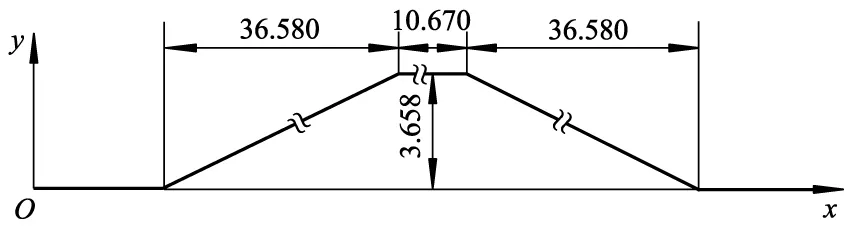
图3 仿真所用双移线路径示意图(单位： m)

3.2 双移线工况仿真

选择双移线(图3)作为试验工况,模拟在高附着路面(μ=0.85)下的高速(105 km·h-1)换道.

仿真参数:m1=6 597 kg;Iz1=35 768 kg·m2;前/后轮轮距dw1=2 m;a1=2 m;b1=2.135 m;轴距L1=4.135 m;Cf=-232 240 N·rad-1;Cr=-600 000 N·rad-1;Rw1=0.269 m.

牵引车与半挂车的路径跟踪情况、牵引车的横摆角速度响应、折腰角状态响应如图4,5所示.

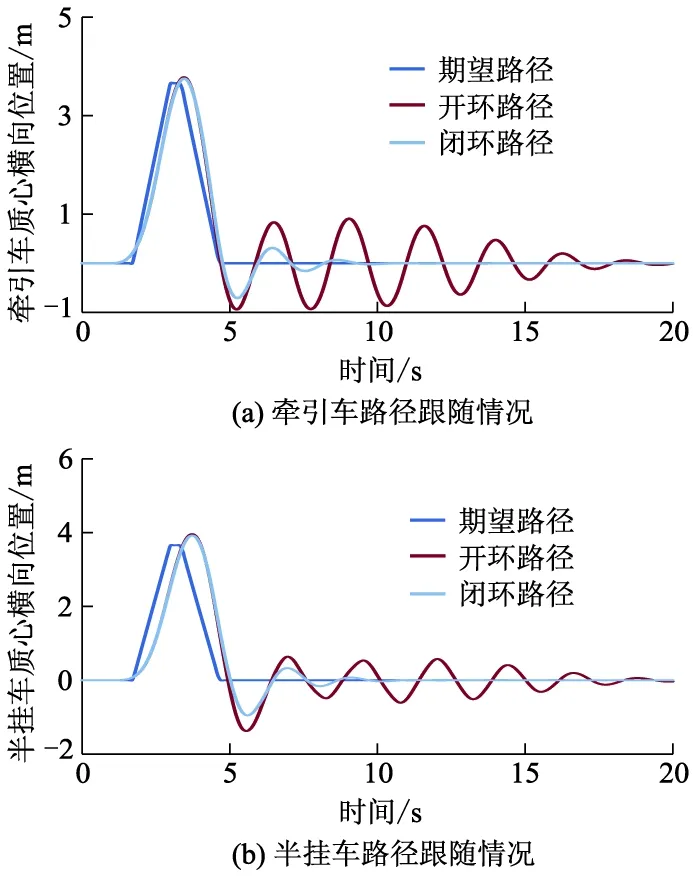
图4 路径跟随情况

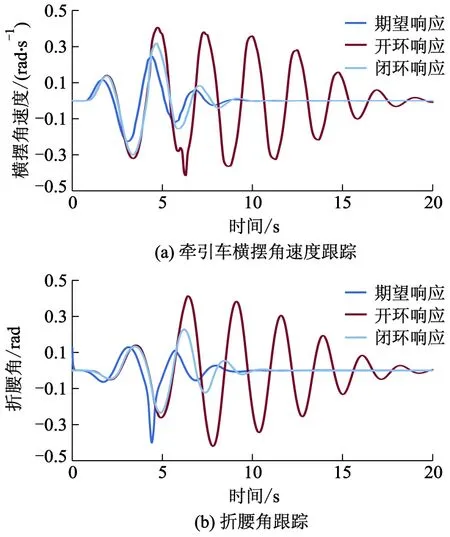
图5 折腰角状态响应

从图4,5可以看出:如果没有稳定性控制系统,牵引车横摆角速度与折腰角响应都严重偏离参考值,路径跟踪出现严重的摆振现象,进行控制后,车辆能较好地跟踪参考响应,摆振现象减弱,路径跟踪得到提升,整车横摆稳定性得到有效提高.

牵引车纵向速度变化如图6所示,稳定性控制系统的介入,使车辆在过弯时也能较好地保持车速稳定.

图6 车速保持

控制量变化及轮速变化分别如图7，8所示.施加控制后,驾驶员决定的前轮转角与AFS系统施加的附加前轮转角关系如图7a所示,DYC系统施加给牵引车和半挂车各车轮的主动制动力矩如图7b所示.有稳定性系统辅助时各车轮的轮速变化状况如图8所示.从图7,8可以看出车辆轮胎处于稳定的工作状态.

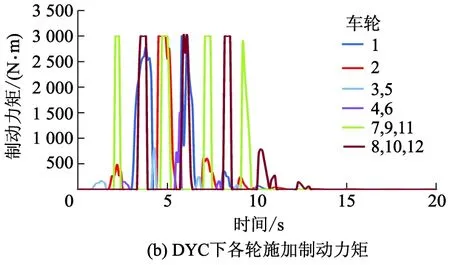
图7 控制量变化

图8 各轮转速变化

3.3 鱼钩转向仿真

车速为55 km·h-1,在低附着路面(μ=0.30)上进行鱼钩转向试验,鱼钩转向的转向盘角度输入如图9所示.

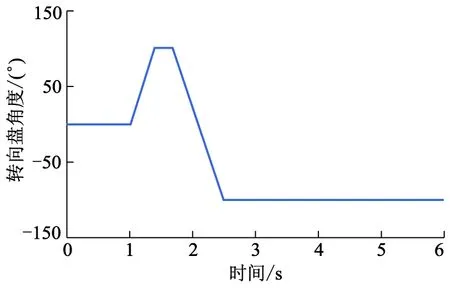
图9 鱼钩转向转向盘角度输入

牵引车的横摆角速度、半挂汽车列车的折腰角和牵引车质心的纵向速度变化如图10所示.

图10 车辆状态变化

从图10可以看出：开环系统在该工况下的行驶过程不稳定,过快的车速导致车辆发生侧滑与折叠,车速猛然降低.在仿真时间10 s附近,折叠导致车辆折腰角达到了第5轮处铰接结构所允许的最大折腰角,致使牵引车的横摆角速度发生剧烈变化,非常不利于驾驶员的操控.施加集成控制的闭环系统则在该工况下运行良好,车辆顺利进入鱼钩转向而没有发生折叠.

控制量以及轮速的变化情况如图11所示,在控制介入时,半挂汽车列车的稳定性大大提高.

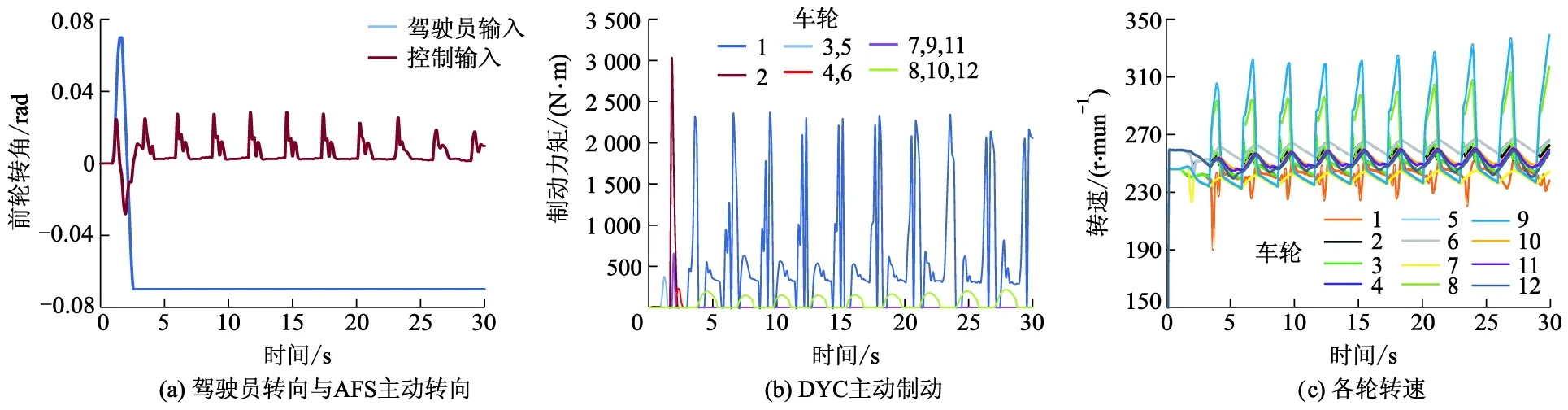
图11 控制量变化

3.4 综合仿真结果

经过大量仿真试验总结得到的开环系统与闭环系统的临界车速对比如图12所示.

图12 临界车速对比

双移线工况下的临界车速是车辆可以稳定通过双移线,并且牵引车质心的偏移量不超过2 m的最大车速;鱼钩转向工况下的临界转速是车辆可以稳定进入鱼钩转向且保持30 s不发生折叠、侧翻等失稳的情况.从图12可以看出：在同一条件下闭环系统的临界车速总是高于开环系统的,进一步说明了集成控制系统的有效性.

4 结 论

以半挂汽车列车的3自由度线性单轨模型作为参考模型,设计了基于滑模控制、模糊控制的AFS/DYC集成控制策略,并在TruckSim中建立了6轴半挂汽车列车整车模型,与Simulink进行联合仿真验证所设计的控制模型.结果表明:TruckSim与Simulink联合仿真是半挂汽车列车稳定性控制系统设计开发的有效手段,所提出的AFS/DYC集成控制策略可以较好地改善整车的横摆稳定性,有效提高了车辆的通过性和行驶安全性.