变温度环境下引信与武器平台时钟同步方法
廖 翔,张 合,李豪杰,高 凯
(1.南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094;2.淮海工业集团有限公司,山西 长治 046012)
0 引言
智能弹药系统需要精确的计时基准以精确控制弹药中各事件的发生时序,并通过计时起点与武器平台的绝对时间相对应[1]。产生精确计时基准的主要方法为:1)用高精度振荡器减小计时基准的随机误差[2];2)用时基校准方法减小环境因素对计时基准的影响[3-4]。引信计时起点主要通过弹丸工作过程中的各种环境信息获得,难以与武器平台上的时钟对应。在无线传感器领域,常采用双向时间戳交换方法进行时钟同步[4]。该方法能够同步测量出当前偏置和当前漂移,当前偏置用来修正当前时钟误差,获取计时起点;当前漂移用来修正计时基准[5]。影响漂移量的因素主要有环境温度和贮藏时间等[6-7]。其中,贮藏时间造成的变化速率十分缓慢,其影响能够在时钟同步中消除。温度造成的时钟漂移量变化与环境温度的变化速率有关,当温度变化较快时,计时基准与同步结果有误差。减小温度漂移影响的方法主要有提高时钟同步的频率和预测不同温度下的时钟漂移量两种[8]。时钟漂移的预测方法有两种:1)振荡器出厂时给定的温度-频率(TF)函数预测;2)在时钟同步过程中测量当前温度,通过多次时钟同步形成TF表,利用TF表插值预测两次同步之间的时钟漂移[9-11]。
将双向时间戳交换方法应用于引信时钟同步领域存在的问题主要包括:偏置和漂移测量需要在同步源和终端之间多次交换绝对时间信息,采用出厂TF函数进行温度漂移预测进度较低,TF表插值法需要多次同步,不适用于引信装定。针对上述问题,本文提出了变温度环境下引信与武器平台时钟同步方法。
1 时钟同步模型
为提高温度变化环境下的时钟精度,我们采用两阶段时钟同步方法,该方法由装定信息同步和温度信息跟踪两个阶段组成,如图1所示。时钟同步所需要的输入包括:装定信息,装定过程中的初始温度信息和后续工作过程中的实时温度信息。时钟同步的输出结果为实时漂移α(t),时钟的实时输出结果t为式(1),式中τ为时间积分变量,t0为计时起点。该方法的工作过程为:在装定信息同步阶段,引信利用装定信息估计初始漂移并测量初始温度。在温度信息跟踪阶段,引信利用初始温度和初始漂移估计工作过程中的实时漂移,并对其时钟进行自校准。
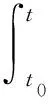
(1)

图1 时钟同步原理框图Fig.1 Block of clock synchronization step
2 装定信息同步方法
基于IEEE1588的双向时间戳交换(TWTE)时钟同步方法可以同时获得初始时刻和初始漂移[6]。该方法的工作过程为:时钟源(CS)向被同步设备(TN)发送当前时间戳信息,TN收到该时间戳后向CS发送其收到信息的时刻,接着CS计算出初始时刻并将初始时刻和当前时间戳发送给TN,TN通过计算两个时间戳之间的差值得到初始漂移。TWTE方法需要CS向TN发送两次当前时间信息作为时间戳,占用大量通信资源,难以在通信资源有限的装定过程中使用[14]。因此,设计了如图2所示的同步原理。该原理要求系统基带码型为带有时钟信息的定长码,一般基带码型均可满足该要求[16],为复原基带码型中的时钟信息,可在信源编码过程中插入等间隔符号。

图2 装定信息同步原理框图Fig.2 Synchronizing by set information
在装定过程中,装定器共发送n个码元,引信共反馈m个码元,如图2所示。在图2中,ts为装定器码元发送和接收时刻,tf为引信码元接收和发送时刻,tsf为采用装定器时钟度量的tf;ds[i]=tsf[i]-ts[i]为装定延迟,df[i]=ts[i]-tsf[i]为反馈延迟;α[i]=tf[i]/tsf[i]-1为单码元时钟漂移。装定信息同步阶段估计的参数为初始时钟漂移α(t0)。为进行温度信息跟踪,还需测量装定过程中引信的初始温度T0并估计时钟漂移预测区间p。
引信和装定器均无法直接获知tsf,因此,引信在接收第i个码元时的时钟漂移为式(2),式中,k为测量码元间隔。与TWTE方法不同,装定器发送的信息中不需要包含时间信息,不占用通信资源。引信直接无法获知ts[i]-ts[i-k],对于定长码,定义装定信息每个码元的长度均为τ,则时钟漂移的测量值αm[i]为式(3),αm[i]与α[i]的关系为式(4),式中,nsi为装定器输出噪声,β[i]为装定器时钟漂移,nsi为引信检测噪声。
(2)
αm[i]=(tf[i]-tf[i-k])/kτ-1
(3)
(4)
假设装定器经过良好校准,即E(β[i])=0,则在整个装定过程中α(t0)的期望为式(5)。
(5)
假设装定器经过良好校准,即E(β[i])=0,则在整个装定过程中α(t0)的期望为式(5)。
由式(5)可知,E(αm)是E(α(t0))的有偏估计,因此采用递归最小二乘滤波法[5]估计α(t0)。同时,为了减小预测区间p并简化计算过程,改进了递归最小二乘滤波法,使其能够在迭代过程中估计p。算法的更新过程如式(6)至式(10)所示。α的更新方法为为式(6),式中,r为阶数,l为循环次数,λi为测量值的权重,αm[l+1-i]为α的最后r个测量值,λl=[λl+1-r,…,λn],αml=[αm[l+1-r],…,αm[l]]。λl的更新方法为式(7),式中,η为遗忘系数,Pl为最小二乘系数矩阵,其更新方法为式(8)。预测区间p更新方法为式(9),其中标准差σl的更新方法为式(10)。
(6)
(7)
(8)
pl=pl-1+2(αl-αl-1)σl+(l-1)(αl-αl-1)2
(9)
σl=σl-1+(l-1)(αl-αl-1)
(10)
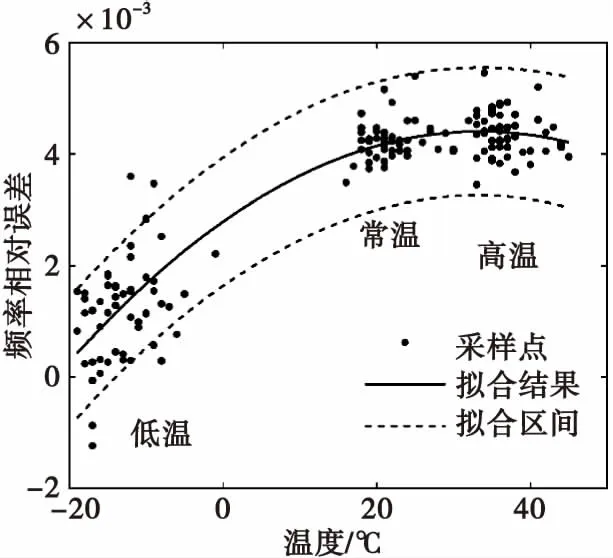
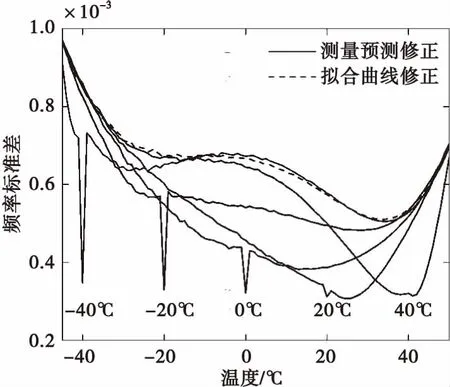
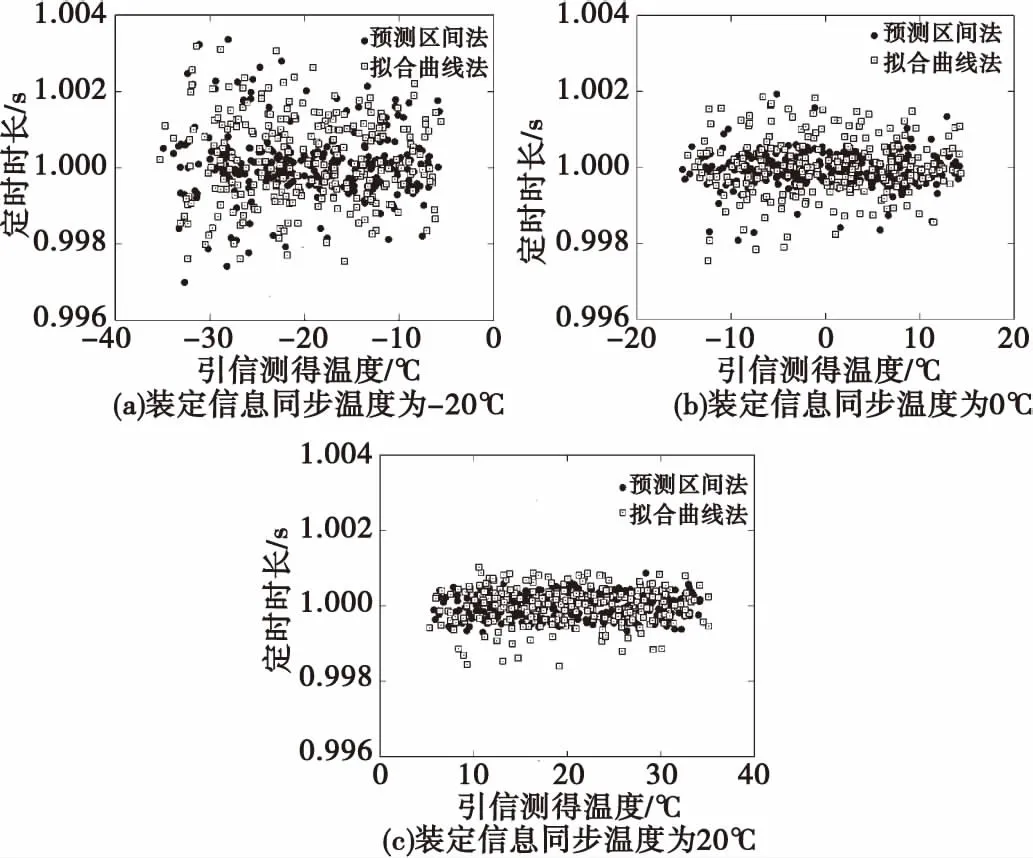
算法参数初始化为r=3,l=0,α0=0,λ0=0,P0=I/r,p0如式(11)所示,σ0=0。算法的迭代过程为:当l (11) 根据表1所列参数对上述算法进行仿真,α(t0)在仿真开始时随机产生,仿真结果如图3所示。图3对每个k值进行2 000次仿真,统计当前k值下α(t0)测量结果与真实值的标准差和p的平均值。从图中可以看出,当k=1 bit时α(t0)测量标准差及p均很大,随着k增大二者迅速减小,至k=3 bit时达到最小值,而后缓慢增大。均值法α(t0)测量结果标准差小于滤波法,但得到的预测区间更大。 表1 装定系统仿真参数 图3 同步码元间隔与频率漂移测量误差的关系Fig.3 α(t0) standard error versus symbol interval 引信采用内部硅振荡器作为其时钟源,参数与表1一致,根据硅振荡器原理,引信时钟频率ffuze(T)随环境温度的变化函数为二次函数式(12),式中,Tb为基准温度,C1和C2为频率变化系数[11]。由于振荡器参数的误差,各个引信的Tb、C1和C2不相同,无法直接采用式(12)对获得不同温度下的时钟频率[13]。 (12) 在对某批次引信进行不同温度下时钟频率抽样测试后,得到温度-频率误差分布如图4所示。图中时钟源的标称频率为1.5 MHz,实线为拟合得到的二次曲线,虚线为预测区间。将式(12)转换为实际频率与标称频率的相对误差δ与温度的函数式(13),式中,β0、β1和β2为频率误差系数,令β=[β0,β1,β2]为系数向量。频率相对误差与时钟漂移的关系为δ=-α。对于同批次的任意一个引信,β利用前节得到的初始漂移、初始温度和图4预测。 图4 频率误差相对于温度的变化采样结果Fig.4 Sampling result of frequency error versus temperature 根据预测区间的定义可知,对于同批次多数时钟源,曲线(13)上所有的点均位于预测区间内,且通过坐标为[TM,δ(TM)]的测量点M。因此,对于一个测量点M,所有可能的曲线(13)为两条二次曲线围成的区间,该区间为优化问题(14)的解,式中β1和β2为两条边界曲线的参数,T=[1,T,T2];为减少测量误差导致测量结果超出图4上下界的情形发生,需要将上下界p叠加,C1和C2中Tu和Tl为将p叠加入图4后得到的预测区间上下界。边界条件C1和C2表示边界曲线上的所有点均在预测区间内,C3表示两条边界曲线均需通过测量点M,C4和C5表示两条边界曲线均开口向下。 δ=β0+β1T+β2T2 (13) (14) C4:β12≤0,β22≤0。 优化问题(14)为一非线性连续优化问题,为得到其最优解,离散化并弱化其约束为问题(15),式中i=1,2。C5中Tl为温度最小值,C6中Tu为温度最大值。C5和C6分别表示在温度最大值和最小值处的边界条件。 (15) 显然,当β1为联立式(16)和C3的解,β2为联立式(17)和C3的解时优化问题(15)达到最优。 (16) (17) 由于优化问题(15)是优化问题(14)的约束弱化版,还需要判断得到的β1是否满足边界条件C1,β2是否满足边界条件C2和C5,若满足,则得到预测区间。若β2不满足C5,则令β22=0,代替式(17)中的一个方程,重新求解β2,得到的两个结果中必然有一个满足边界条件C2,以该结果作为新的β2。若β1不满足C1或β2不满足C2,则计算β1与βl或β2与βu的距离最远的点Tc,若Tc>Tm,则用Tl,Tm和Tc三个点求解得到新的β1或β2,若Tc 在测量温度分别为-40 ℃、-20 ℃、0 ℃、20 ℃和40 ℃时,仿真不同温度的频率漂移修正结果与实际温度的标准差如图5所示。图5中实线为利用测量结果修正的频率漂移,虚线为利用统计结果直接修正的频率漂移。从图中可以看出,利用测量修正的频率漂移在多数情况下优于利用统计结果修正,随着实际温度远离被测量温度,修正结果趋近于统计结果修正。当测量结果温度处于20~40 ℃时,在当前测量结果附近能够获得接近测量结果的修正精度,当测量结果温度小于20 ℃时,修正偏差较大。 图5 温度跟踪修正与拟合曲线修正标准差对比Fig.5 simulation result of frequency standard error 通过不同温度下的1 s定时试验以验证时钟同步效果。试验采用50个与图4相同批次的时钟,其标称参数与表1相同。对于每个时钟采用的试验方法为:1)在设定温度下运用装定信息同步法校准初始时钟漂移,记录初始时钟漂移校准结果和1 s定时结果;2)改变温度,根据初始时钟漂移校准结果校准当前时钟漂移结果,记录1 s定时结果;3)重复步骤2和3至试验完成。用图4的统计拟合结果校准时钟漂移,记录1 s定时结果,用该结果与本文所述两阶段时钟同步方法进行对比。 分别在装定信息同步温度为-20 ℃,0 ℃和20 ℃的条件下进行试验,试验中设置温度改变量分别为±5 ℃和±10 ℃。50个时钟的试验结果如图8所示。对比图6(a)、(b)和(c)可以看出,不论采用何种同步方法,其精度都随同步温度升高而升高,与仿真结果图5一致。从图6中可以看出,温度测量修正法的极差与统计拟合修正法相似,但统计拟合法结果分布较为均匀,而采用预测修正法时,大部分时钟的定时结果集中分布在1 s附近。出现该现象的原因为,温度测量修正法利用装定信息同步阶段得到的时钟信息,减小了频率漂移的预测区间。但该方法假设所有时钟的频率漂移测量结果均在图4的边界范围内,而实际情况下,部分时钟可能出现超出边界的频率漂移,导致部分时钟的实时校准结果误差偏大。 图6 1 s定时试验结果Fig.6 1 second timing experiment result 对图6中的数据进行了统计以定量对比本文所述两阶段时钟同步法和统计拟合法的同步效果,其结果如表2—表4所示。表2—表4列出了时钟不同温度、不同方法下的1 s定时标准差。从表中可以看出,装定信息同步法的时钟同步效果与温度无关,且效果远好于统计拟合修正法。温度跟踪法和统计拟合修正法与温度有关,温度跟踪法的标准差比拟合修正法小2×10-4s,验证了温度跟踪法优于统计拟合法。 表2 装定信息同步温度为-20 ℃的1 s定时标准差Tab.2 1 Second timing standard error when the set information synchronization at -20 ℃ 表3 装定信息同步温度为0 ℃的1 s定时标准差Tab.3 1 Second timing standard error when the set information synchronization at 0℃ 表4 装定信息同步温度为20 ℃的1 s定时标准差Tab.4 1 Second timing standard error when the set information synchronization at 20℃ 本文提出了变温度环境下引信与武器平台时钟同步方法。该方法改进了双向时间戳同步方法,采用事先约定的定长码元代替绝对时间交换进行时钟同步,且利用引信时钟源温度漂移统计结果和装定信息同步阶段测量结果进行温度漂移预测。经过仿真和试验验证表明,该方法能够获得稳定的时钟起点,并在一定的温度范围内获得比仅用时钟源温度漂移统计结果修正和TF函数修正更小的时钟同步误差。

3 基于温度跟踪的时钟自校准
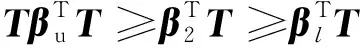
4 试验



5 结论

