科研项目财务绩效综合评价——一个基于AHP 方法的理论初探

（中国石油天然气股份有限公司勘探开发研究院（北京院）计划财务处北京100083）

一、国内外研究现状

1999年，财政部、原国家经贸委、人事部、国家计委颁布了《国有资本金效绩评价规则》和《国有资本金效绩评价操作细则》（财统字［1999］2号）。2006年国务院国有资产监督委员会颁布了《中央企业综合绩效评价暂行办法》，该办法提出建立综合评价指标体系，全面对企业的资产质量状况、债务风险状况、盈利能力状况、经营增长状况以及管理绩效等进行综合、全面的评价。与此同时，我国学者也对企业的财务绩效展开相关研究，蔡昌、田依灵（2017）利用时间序列回归模型以2008—2013年的上证 A股和深证 A股上市公司为样本，基于产权税收理论，实证分析了产权性质、税收负担和企业财务绩效的相关性；赵刚、许德惠（2017）借助基于 PLS的结构方程建模技术，研究企业资源对供应商整合及财务绩效的影响；卢宏亮等（2016）将B2B品牌形象和 B2B-OEM关系价值放在一个框架中，探讨了二者对B2B财务绩效的影响以及B2B品牌形象对OEM关系价值感知的影响。

国外方面，企业财务绩效评价指标体系主要有两种，分别是沃尔评价指标体系和EVA评价体系。此外，美国学者Altman通过建立的Z-SCORE模型，分析企业的财务绩效。之后的学者继续优化此模型，产生了基于此模型的诸多变种，在企业财务绩效评价方面发挥了重要作用。Bell利用神经网络模型评价企业的财务绩效，此模型具备预警机制，对预测企业的财务风险发挥了重要的作用。

本文尝试用AHP（层次分析法）方法，构造科研课题财务绩效评价指标体系，以综合、全面地反映科研项目的财务完成情况。

二、本文研究方法

层次分析法（AHP）是美国运筹学家匹兹堡大学教授A.L.Saaty于20世纪70年代针对解决大型的复杂问题而提出的一种能综合进行定性与定量分析的方法。AHP法将所研究的问题结构化、层次化，实现了定性研究和定量研究的结合，最终通过一致性（CR）检验在一定程度上解决了指标赋权的主观性，从而提高了主观决策过程的科学性，是分析多目标、多因素、多准则复杂大系统的有力工具。

笔者将科研项目经费预算总结为呈树状结构的预算体系。“科研项目总预算”下设一级明细预算，一级明细预算下设二级明细预算，以此类推建立起树状结构的科研项目预算体系。构造判断矩阵和相对权重计算是由定性过渡到定量的核心，也是由主观判断到定性分析的关键所在。根据科研项目经费预算的树状结构体系编制科研项目财务绩效评价矩阵（见表1）。

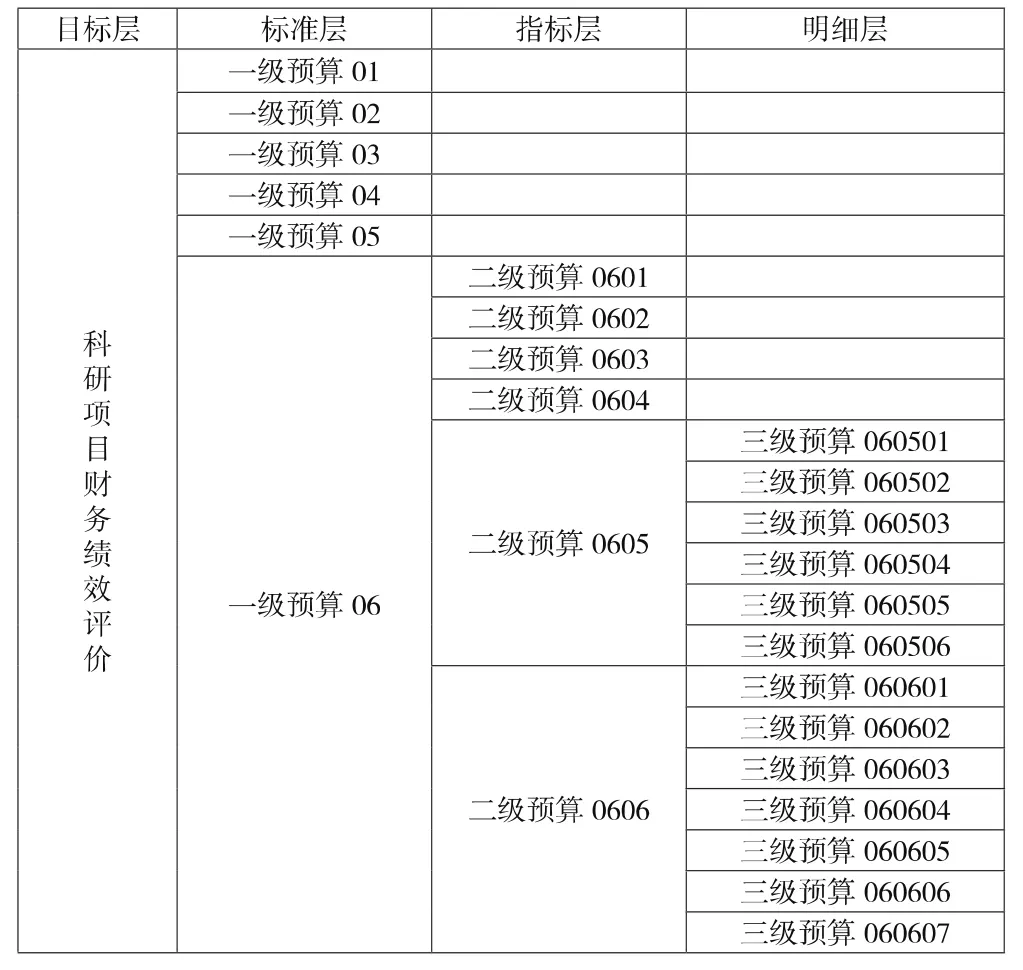
表1 科研项目财务绩效评价矩阵表

科研项目财务绩效评价矩阵依据科研项目预算的级别分为四个层次，分别为：目标层、标准层、指标层和明细层。其中“科研项目财务绩效评价”为判断矩阵中的目标层，因其构建的模型就是用于评价科研项目的财务绩效；标准层为科研项目的各一级预算；指标层为各一级预算下的二级预算；相应的明细层即为各二级预算下相应的明细项目。

三、判断矩阵权数确定方法

权数的确定是判断矩阵构造的核心。学术界对模型中权数的确定方法不一，主要有专家打分法、会议讨论法等。鉴于科研项目预算的可获得性，本文采用预算百分比法进行权数的确定。具体操作为：将课题归类，将属于同一类的课题归集到一起，课题归类的标准依决策者的需要而定；将同一类别课题的总预算以及各级明细预算分别加总，亦即将判断矩阵中的各标准层、指标层、明细层的预算明细加总；将加总后的各级预算明细与所属的上一级预算合计做商。例如：将各级次预算与所属上一级的预算合计数做商；经过“做商”的处理后，即能得出同一级次各预算明细与上一级预算合计的比例，即能够比较同级预算之间的相对重要程度。

四、模型计算方法概述

根据Saaty1—9比率标度法（见表2），可为同一级次的各明细预算赋值，即构成所谓判断矩阵A=（aij）mn。

表2 Saaty1—9表

（一）建立判断矩阵。

（二）将矩阵按行相乘即得到M矩阵。

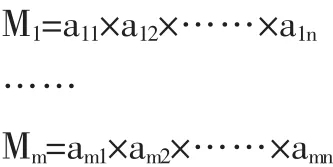
（五）计算判断矩阵的最大特征根λmax。

（六）进行一致性检验。由于人们的认知不尽相同，对各类因素的分析势必存在一定程度的偏差，这就需要对判断矩阵进行一致性检验。首先引入度量判断矩阵偏离一致性的指标，CI=（λmax-n）/（n-1），其次由 RI值表（见表3）查出对应的评价随机一致性指标。

表3 RI值对照表

（七）计算CR值。CR=CI/RI，只有当CR值小于0.1时，矩阵中各项的权数才能被应用于模型中。用这种方法可以分别计算科研项目财务绩效评价矩阵中每个层次预算项目的相对权重。科研项目财务绩效综合得分情况很大程度上取决于各明细级预算项目相对权重。隶属于同一预算项目下同一级次的预算明细权数可以通过将其在本级次中的相对权重乘以其所属的上一级预算在它的同一级预算中的相对权重值的方法取得。举例来说：通过上述权数的计算，我们得到一级预算中“06”的相对权数为A，“0605”在所有“06”预算下的相对权数为 B，“060503”在“0605”中的相对权数为C，则在评价科研项目的财务绩效时，应该赋予“060503”的权值为 A×B×C。

（八）计算具体某一明细项的得分。我们采用权数值与离差值相乘的方法计算某一明细预算项的得分。离差表示为该项支出与预算之差的绝对值。用该明细预算项相对于总预算的权重值乘以该项预算的离差即为该项预算明细的实际得分。如此分别计算出本预算项目下的各明细预算项目的得分，然后将各最明细预算的得分相加即为该项目的财务绩效综合得分。

五、应用举例

本文以某研究机构承担的科研项目为例。该机构中科研项目财务绩效评价体系由三个层次组成，分别为目标层、标准层和指标层，无明细层。目标层为“财务绩效评价”，总括性地反映评价项目的得分，得分高即财务绩效高。标准层预算分为条件配套费、办公费、会议费、差旅费、材料费、技术配套费、技术服务费。在指标层预算上，条件配套费包括租赁费、维修费、运输费；技术配套包括图书资料费、培训费、设计制图费、资料解释费、咨询评审费、测试化验加工费。如表4所示。

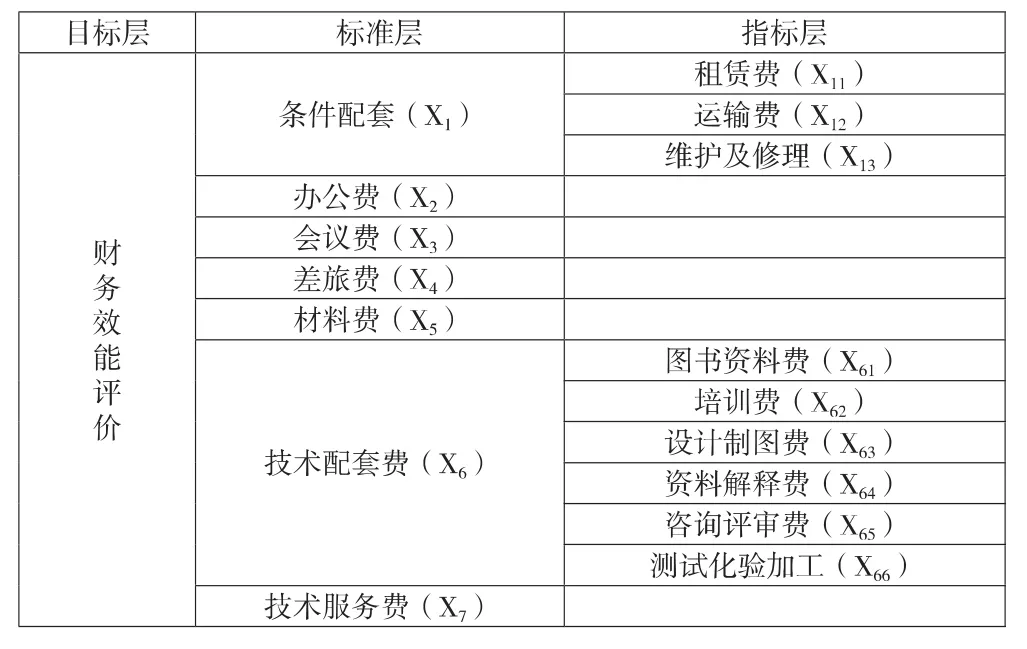
表4 评价体系指标表

根据上述建立的指标体系，该项目财务效能评估集可以标记为 X={X1，X2，X3，X4……X7}，每个因素又有具体的评价指标，依次建立指标集 Xi={Xi1，Xi2，Xi3……}，其中 i=1，2，3，4，5，6。

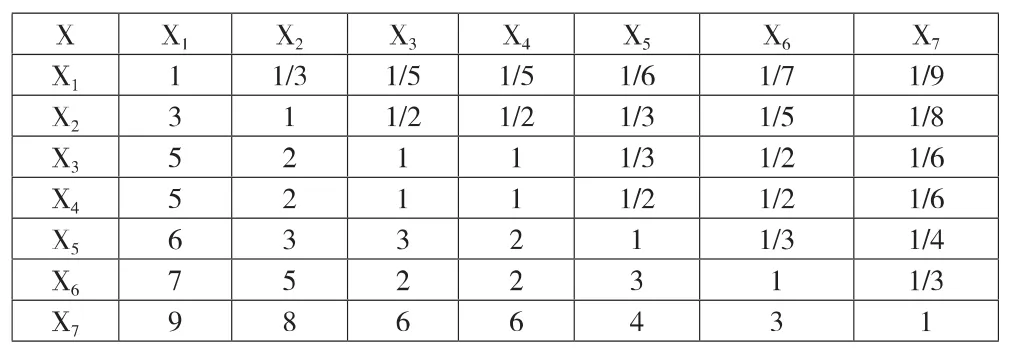
表5 标准层判断矩阵

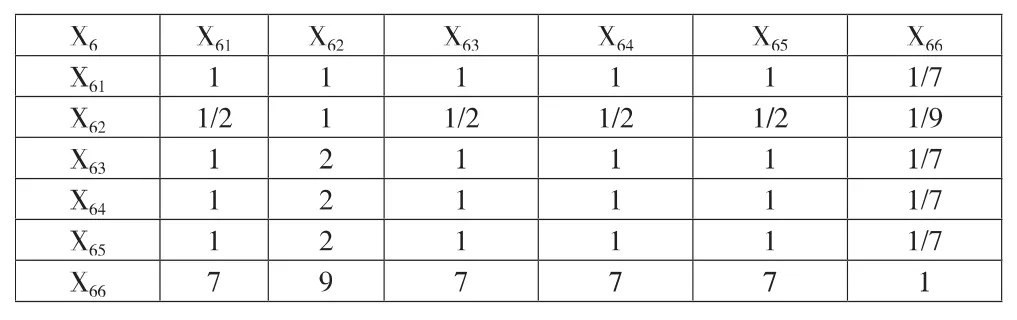
表6 技术配套费判断矩阵

表7 条件配套判断矩阵

根据下级预算占上级预算的比重确定各指标权数。最终得到各级次的判断矩阵，判断矩阵见表5—表7。

（一）将矩阵按行相乘，得到新向量M。分向量依次为：M1=0.00003527，M2=0.00625，M3=0.27777，M4=0.41666，M5=9，M6=140。

（三）特征向量。所得的特征向量为w=（0.0004，0.001461，0.003772，0.004175，0.009，0.017873，0.069005）T。

（四）计算判断矩阵的最大特征根λmax。

进行一致性检验。首先引入度量判断矩阵偏离一致性的指标，即 CI=（λmax-n）/（n-1）=0.041987，其次由RI值对照表查出对应的评价随机一致性指标RI=1.32。

（五）根据CR=CI/RI计算出CR。CR=0.041987/1.32=0.03＜0.1，因此各指标层对目标层的重要性具有较满意的一致性，故w=（0.0004，0.001461，0.003772，0.004175，0.009，0.017873，0.069005）T可以作为一级预算判断矩阵的权重。用同样的方法可以求出：

技术配套判断矩阵的特征向量为：

从而我们可以得出汇总的一级预算指标和二级预算指标的综合权重，详见表9。

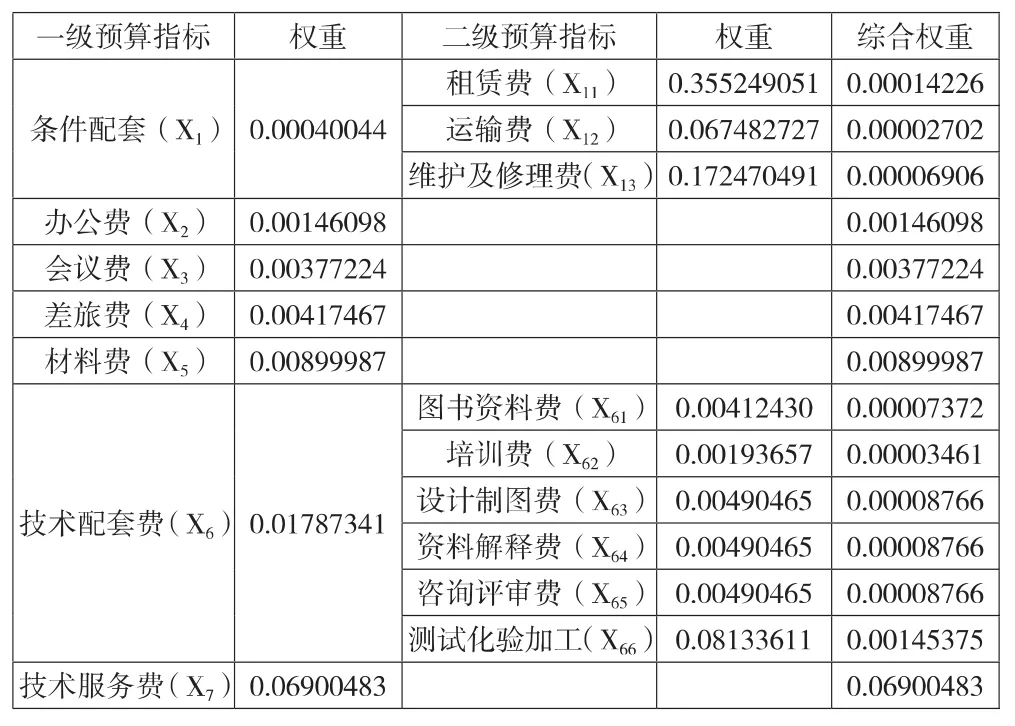
表9 标准层与指标层综合权重表

根据此综合权重表，我们可以构建出该机构科研项目财务效能评估综合模型：

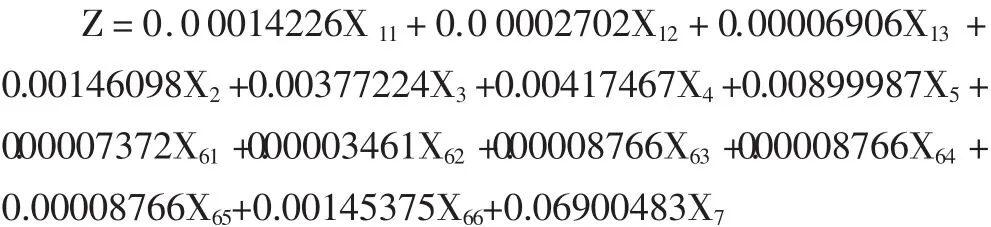
实际应用中，在比较同一机构不同项目间财务绩效时，Z值高的科研项目的财务绩效比Z值低的科研项目财务绩效高。

六、结束语

在缺乏科研项目财务绩效有效定量综合研究的情况下，引进AHP层次分析方法可以实现由定性到定量、由局部到综合的转变，提高评估的系统性和科学性。使用AHP方法下的科研课题财务绩效评估模型，可以把包括各个预算明细重要程度等的所有因素综合地考虑在内，它扬弃了过去简单的依靠预算完成情况衡量课题财务支出情况的局面，而是以立体、完整的分析框架评价课题财务支出情况，对相关管理部门制定决策有用的信息更具指导意义。