铁路钢轨网格化维修规划优化编制模型

白 磊，贾传峻，李 擎，刘仍奎，孙全欣

(1.北京交通大学交通运输学院，北京100044；2.北京易华录信息技术股份有限公司，北京100043)

0 引言

铁路钢轨是铁路轨道设备最重要的组成部分.铁路钢轨维修是指为保持、恢复和改善铁路钢轨质量状态，延长其使用寿命，确保其实现所期望的功能，铁路管理者采取的所有技术和管理活动的集合.优化编制铁路钢轨维修规划，对避免安排“过维修”“欠维修”这些不恰当的维修活动，合理分配维修资源，降低维修成本，确保列车持续安全、平稳运行等具有重要意义.

目前，我国铁路现场轨道设备维修以故障修、周期修为主，正逐步向基于状态的预防修转变.铁路轨道设备维修规划的相关规章较少，铁路现场缺乏统筹编制较长时间跨度的维修规划，管理者一般按照年度制定不同管辖单位的维修任务量、大修任务量，多以百分比的形式体现.国内外专家学者大多采用组合优化方法[1-5]，研究铁路轨道设备维修规划、维修计划的编制问题.如Caetano等[1]提出了一个以成本最小、轨道可靠性最大为优化目标的铁路轨道维修规划优化编制模型.郭然等[4]采用整数规划方法，提出了一个面向区域路网的铁路轨道维修计划优化编制模型.周宇等[5]提出了一个0-l整数型轨道状态最优综合维修计划编制模型.

上述研究均假设提出的模型能准确预测轨道设备未来的状态，这忽略了轨道设备未来劣化状态的不确定性.Markov决策过程方法(Markov Decision Process，MDP)以状态转移概率的形式来描述设施设备状态预测的不确定性.目前，采用Markov决策过程方法解决铁路钢轨维修计划编制问题的直接研究较少，该方法的研究多集中在道路路面的维修规划编制问题[6-7].

本文将基于铁路基础设施网格化管理思想，将线性、连续的铁路钢轨设备，按照某一长度，划分为若干连续等长的小区段，以小区段作为基本研究对象，采用Markov随机过程理论方法，研究提出一种铁路钢轨网格化维修规划优化编制模型(Optimal Maintenance Planning Model for Railway Rail Grids，OMPM-RGG).本文的创新点体现在以下几方面：将Markov决策过程方法，首次应用到铁路钢轨维修规划编制问题中，考虑到了铁路钢轨未来劣化状态的不确定性；在编制维修规划时，考虑到了铁路钢轨状态劣化的异质性，个性化地描述每个钢轨网格的状态劣化规律，编制出的维修规划更具针对性.

1 铁路钢轨网格的基本概念

依据铁路基础设施网格化管理思想[8]，铁路网格是指将线性、连续、带状布局的铁路线路按一定规则，划分成的若干相邻等长的“小区段”，如图1所示.铁路网格是由其相应里程范围内的不同专业铁路基础设施构成的，是这些铁路基础设施的综合体.每个铁路网格单元用Gi表示，i=1,2,…,I，其中I表示铁路网格单元的总数.钢轨是轨道结构最重要的组成部分，具有承载轮重、横向上引导车轮、提供光滑的运行表面等功能.钢轨网格是指铁路网格中的钢轨部分.在本文中，钢轨网格的长度设置为1 km.

图1 铁路网格示意图Fig.1 Diagrammatic sketch of railway grid

《钢轨伤损分类》(TB/T 1778-2010)规定，根据钢轨磨耗量和疲劳伤损程度等，单根钢轨的伤损状态等级分为轻伤、重伤和折断等.本文钢轨网格的整体状态采用每公里钢轨重伤数进行评定，该指标能直观反映铁路线路钢轨的伤损情况，也是判断铁路线路是否需要整体换轨大修的重要依据.通过设置不同的管理阈值，钢轨网格整体状态可划分为若干劣化等级，不同的状态等级可对应不同的维修策略.

2 铁路钢轨网格化维修规划优化编制模型

本文提出的铁路钢轨网格化维修规划优化编制模型OMPM-RGG由以下两个子模型构成：

(1)铁路钢轨网格化状态劣化规律子模型，采用多阶段Markov模型MEMM，综合考虑各类异质性因素影响，个性化地描述钢轨网格状态劣化规律；

(2)铁路钢轨网格化维修决策子模型，采用Markov决策过程MDP，以一个较长规划周期内的期望总成本最小为目标函数，建立基于状态的维修策略模型.

2.1 铁路钢轨网格化状态劣化规律子模型

铁路钢轨随着上道服役时间的增长，钢轨伤损状态会不断劣化.钢轨在上道初期，劣化速度较慢，随着累计通过总重的增加，劣化速度逐渐加快[9].同时，钢轨状态劣化是一个随机过程，具有不确定性[10].这是由于钢轨状态劣化受多种异质性因素影响，现有的检测手段在实际的运营线路上不能获得这些异质性因素的全部信息.因此，在不同的生命周期阶段，钢轨状态劣化的速度不同，且劣化具有不确定性.

基于上述铁路钢轨的状态劣化特点，本文将钢轨网格的状态劣化过程细分为若干阶段、整体状态划分为若干状态等级，利用Markov随机过程理论，描述在相邻两次检查间的钢轨网格状态等级变化的不确定性，钢轨网格在不同状态劣化阶段中的寿命分布规律采用不同的指数寿命分布函数进行描述.

假设tA、tB表示该钢轨网格相邻两次检查日期，钢轨网格检查周期Z=tB-tA.X(tA)表示在tA时刻钢轨网格的状态等级，表示状态等级的总数；X(tB)表示在tB时刻钢轨网格的状态等级，，如图 2所示.图中的圆形点表示钢轨网格当前的状态等级，竖实线箭头表示钢轨网格由状态等级i-1突变到i，横虚线箭头表示钢轨网格持续地处于状态等级i，竖实线箭头、横虚线箭头共同描述了钢轨网格状态的劣化过程.钢轨网格在tA时刻状态等级为条件下，在tB时刻状态等级的Markov转移概率为

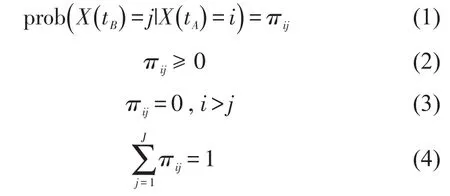
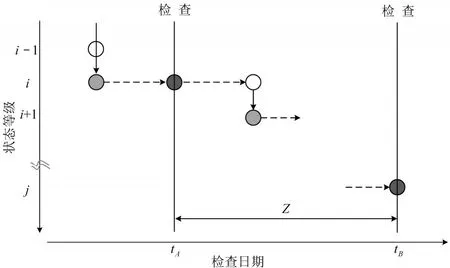
图2 钢轨网格状态劣化过程示意图Fig.2 Schematic map of deterioration process of a rail grid condition

采用Tsuda与Kobayashi等提出的多阶段指数Markov模型MEMM[11-12]，确定钢轨网格的状态转移概率，如式(5)所示.其中，钢轨网格由状态等级i劣化到i+1的失效率用θi表示，i∈{1 ,2,…,S-1}.钢轨网格状态等级由i变化到S的状态转移概率如式(7)所示.

同时有

在不采取维修活动的前提下，随着上道服役时间的推移，钢轨设备状态只会逐步劣化，πij=0(i＞j).由于状态等级S为Markov吸收态，当钢轨网格状态等级为S时，根据Markov模型性质，其状态转移概率πSS=1.

假设1条钢轨线路按照固定长度划分为K个钢轨网格，Gk表示第k个钢轨网格，k∈[1 , 2,…,K].θki表示钢轨网格Gk的失效率，i=1,2;k=1,…,K，将其定义为

式中：χk是钢轨网格Gk的异质性因素；M是异质性因素的总数；βi表示χk对Gk由状态等级i劣化到状态等级i+1的贡献程度，i∈[1 , 2,…,S-1]；β为待估参数变量.

2.2 铁路钢轨网格化维修决策子模型

基于状态的铁路钢轨维修策略模型，采用Markov决策过程MDP进行构建.该模型的目标函数是整个规划周期的期望总成本最小，决策变量是规划周期内的维修策略，规划周期内的钢轨状态约束折算为成本，作为目标函数的一部分.该模型的关键要素为

(1)℘=[1,2,…,S]表示钢轨网格有限的状态等级集合.

S表示状态等级的总数；Xt表示在t时刻的钢轨网格的状态等级，Xt∈℘.Xt=1表示钢轨网格刚上道服役或经过大修维修，处于最好的状态.

(2)ℵ表示钢轨网格有限维修类型的维修活动集合.

At表示在t时刻采取的维修活动，At∈ℵ.At=a表示在t时刻采取了维修类型为a的维修活动；At=0表示在t时刻不采取任何维修活动.

(3)πij(a)表示不同类型维修活动作用下钢轨网格状态转移概率.

πij(a)表示当钢轨网格在t时刻的真实状态为i，采取维修活动At=a时，在t+1时刻钢轨网格状态为j的概率为

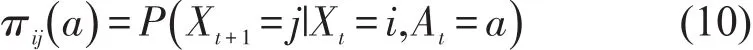
状态转移概率πij(At)随维修活动At的不同而变化.若不采取维修活动，At=0，钢轨网格状态转移概率πij(0)，可由第2.1节提出的状态劣化规律子模型得到.

(4)Rt表示检查、维修活动的成本函数.

Rt表示钢轨网格在t-1时刻采取维修活动At-1的成本ξ1(Xt-1,At-1)，即

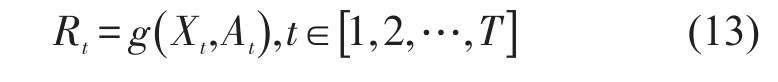
式中：g(Xt,At)表示钢轨网格在t时刻的维修成本，由t时刻的钢轨网格状态、采取的维修活动类型的决定.若在t时刻不采取维修活动，At=0，ξ1(Xt),0表示在t时刻钢轨网格状态继续恶化带来的损失.

(5)δ表示成本随时间推移折扣率.

δ用于衡量未来成本相对于当前成本的重要程度，其含义是t时刻的维修成本仅价值t-1时刻的δ，δ＜1表明当前成本比未来成本更具有价值.

规划周期内的总成本由以下两部分构成：①维修活动的成本g(Xt,At)，是钢轨网格状态Xt、维修活动At的函数；②规划周期结束时的钢轨网格剩余价值SVT+1=u(XT+1)，是规划周期结束时钢轨网格状态XT+1的函数.It表示钢轨网格从初始时刻到t-1时刻时间跨度内的钢轨网格初始状态、维修活动策略构成的向量，即

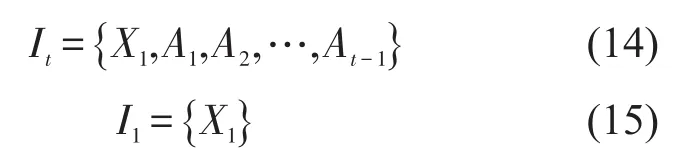
模型OMPM-RGG的目标是确定出1组维修策略At(1≤t≤T)，使得整个规划周期内的期望总成本最小.vt(It)表示从t时刻开始至规划周期结束时的最小期望总成本.vt(It)可通过式(16)和式(17)递归得到.

3 实例验证

3.1 背景介绍

本实例收集整理了2010年1月～2016年1月期间的陇海线上下行K1397+000～K1720+000范围内的47 304条钢轨伤损数据，以该里程范围内的648个钢轨网格为基本对象，研究这些钢轨网格个性化的状态劣化规律，在此基础上求解钢轨网格10年规划周期内的最优维修策略.规划周期的基本粒度是年，整个规划周期的时间长度T=10.作者采用R编程语言[13-14]实现模型OMPM-RGG的构建与求解.

根据在兰州铁路局现场的调研情况，本实例将陇海线钢轨网格状态划分为3个劣化等级，，每一个状态等级的划分标准及相应的维修策略如表1所示.如当某一钢轨网格的每公里钢轨重伤数≥5，其状态等级为3时，需立即对该钢轨网格内的钢轨安排整体换轨的大修作业.

表1 陇海线钢轨网格状态等级划分标准Table 1 Standards of condition rank of rail grids in the Longhai railway

在本实例中，陇海线钢轨网格维修活动的类型包括3类：

根据现场调研，可得到陇海线钢轨不同类型维修活动的费用.本实例中成本随时间推移的折扣率δ取0.9.

3.2 模型结果分析

在本实例中，钢轨网格的检查周期T为30天.采用以下3类异质性因素：小半径曲线(半径r≤600m)地段长度占钢轨网格长度的比例χ1k、大坡道地段(坡度|i|≥12‰)长度占钢轨网格长度比例χ2k、归一化通过总重χ3k，确定钢轨网格Gk的失效率θki.

表2是求解出的模型OMPM-RGG中的待估参数β=(β1,1,β1,2,β1,3,β2,1,β2,2,β2,3)值.在此基础上，结合式(8)和式(5)，可得到不同线路里程位置处的钢轨网格Gk在不采取维修活动条件下的状态转移概率.不同线路里程位置处的钢轨网格，由于受到的异质性因素(χ1,χ2,χ3)作用的影响不同，其状态劣化规律是不同的，其状态转移概率也是不同的.

表2 影响陇海线钢轨网格状态劣化的异质性因素标定系数Table 2 Estimated parameters of heterogeneous factors of rail grids in the Longhai railway

以陇海线上行起点里程为K1595+000的钢轨网格(简写为“钢轨网格RG-A”)为例，编制铁路钢轨维修规划.钢轨网格RG-A的异质性因素χ1k为0，异质性因素χ2k为0，异质性因素χ3k为1，经上述计算，在不采取任何维修活动条件下的钢轨网格RGA相邻两年的状态转移概率πij(A=0)，如表3所示.

表3 在不采取任何维修活动条件下的钢轨网格RG-A相邻两年的状态转移概率Table 3 Condition transition probability matrix of rail grid RG-A without maintenance activities

假设在规划周期的初始时刻(t=1)前，该钢轨网格刚采取了整体更换钢轨大修作业，在t=1时刻该钢轨网格状态等级已知为1.经计算，10年规划周期内的期望总成本最小值v1(I1)为435.954万元，求解出的最优维修策略为

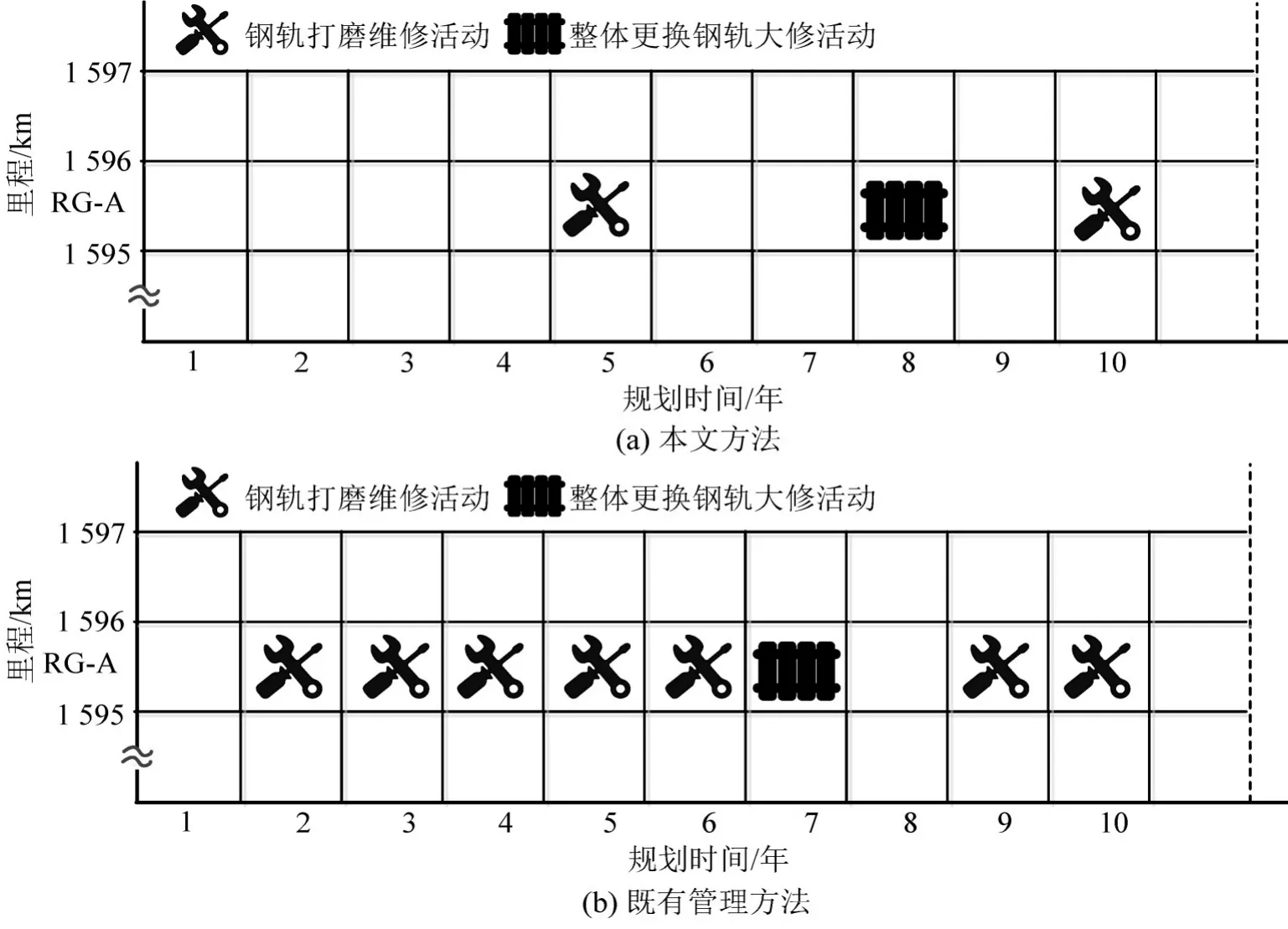
图3 不同编制方法确定出的钢轨网格RG-A的10年维修规划Fig.3 10-year maintenance plan of rail grid RG-A using different models

依据《铁路线路修理规则》(铁运[2006]146号)，中国铁路既有的管理方法一般是按照固定的累计通过总重阈值，周期性地组织安排铁路钢轨维修活动.陇海线上行钢轨网格RG-A的年平均通过总重为96.588 Mt.钢轨网格RG-A的整体更换钢轨大修作业累计通过阈值为700 Mt，钢轨打磨作业的累计通过总重阈值为100 Mt.因此，基于中国铁路既有的管理方法的维修策略为

通过对比式(18)和式(19)，图3(a)与图3(b)可知：

(1)两种维修规划编制模型确定出的整体更换钢轨大修作业的次数是相同的；相较于中国铁路既有的管理方法，模型ORPM-RTG确定出的采取大修活动的时刻推迟了1年.

(2)相较于中国铁路既有的管理方法，模型ORPM-RTG确定出的钢轨打磨次数减少了5次.

(3)对于与钢轨网格RG-A有相同年平均总重的其他陇海线钢轨网格，中国铁路既有的管理方法编制出的维修规划是相同的，但模型ORPMRTG考虑了更多的异质性因素，因此编制出的维修规划是有差异的、更具针对性.

综上分析，相较于中国铁路既有的管理方法，模型OMPM-RGG在准确把握钢轨网格个性化的状态劣化规律的基础上，在保证行车安全的前提下，以整个规划周期内期望总成本最小为目标，能编制出更优化的钢轨网格维修规划，有助于维修资源的合理分配.

4 结论

本文提出了一种新的铁路钢轨维修规划优化编制模型OMPM-RGG.该模型将Markov决策过程方法，首次应用到铁路钢轨维修规划编制问题中，考虑到了铁路钢轨未来劣化状态的不确定性；在编制维修规划时，考虑到了铁路钢轨状态劣化的异质性，个性化地描述了每个钢轨网格的状态劣化规律，编制出的维修规划更具针对性.陇海线的实际案例表明，提出的模型OMPM-RGG优于基于累计通过总重阈值的中国铁路既有的管理方法.中国铁路既有的管理方法缺少考虑多种异质性因素对钢轨状态劣化的影响，缺少考虑整个维修规划周期总成本.

未来作者将在模型OMPM-RGG研究成果的基础上，进一步研究铁路钢轨维修进度计划的优化编制(细化到维修工序层面)、铁路钢轨维修质量的科学评估及铁路钢轨风险管理等.