城市货运车辆选择行为模型及应用

张 戎，李 璐，简文良

(同济大学交通运输工程学院道路与交通工程教育部重点实验室，上海201804)

0 引言

城市货运是满足城市社会经济发展需求的物流活动，对保证城市生产、生活得以正常运行具有重要作用.但是，城市货运也给城市社会、经济带来了显著的外部不经济性.为减少城市货运造成的环境污染、交通拥堵等问题，各地政府相继出台了针对城市货运车辆的通行管制政策.而通行受限的货运车辆无法满足日益增长的城市货运需求，迫使企业采用面包车进行货运活动，由此滋生了“客车载货”等违规行为.“客车载货”的行为不仅增加配送车辆出行数，加剧中心城区的交通拥堵，还存在一定的安全隐患，极大制约了城市交通的可持续发展.

上海市是国内较早实行货运通行管制的城市之一.目前，上海市按企业货车保有量的5%核发通行证，货车持通行证可在工作日7:00-20:00在内环以内通行.该措施是控制市区货运交通量的重要手段，但其弊端也不断显现：日间配送需求无法满足、“客车载货”现象频繁及通行证黑市交易泛滥等，限制了城市货运的健康发展.因此，如何科学制定通行管理政策，已成为城市货运可持续发展的核心问题之一.

国内外针对城市货运通行政策的研究已有一定基础.史新峰等[1]和胡云超等[2]分别采用定性和定量方法评估国内大型城市货运通行管制措施，均得出现行措施会增加配送里程、配送时间和车辆使用数，从而提高配送经济成本、环境成本的结论.张戎等[3]通过借鉴国外城市通行管理的先进经验，提出上海市应逐步放宽中心区时间窗管制，并以通行证拍卖作为过渡手段，最终放开通行证发放的建议.国外研究则以货车车型的选择行为分析，进而评估货运政策的影响为主.Holguin-Veras[4]构建了离散—连续选择模型以评估货运收费政策，得到出行距离、货物品类、单位成本及重量满载率显著影响车型的选择.Qian Wang等[5-6]对丹佛货车出行特征的研究，进一步发现出行属性、目的地属性、货物属性和企业属性均对车型选择行为有影响.Cavalcante等[7]则重点探究货物价值和出行距离对加拿大安大略省货车车型选择行为的影响.

综上所述，既有研究考虑货运通行管制政策因素对货车车型选择行为的影响较少.基于此，本文以上海市为例，选取限行时段进入市中心(内环以内)配送的货车为研究对象，构建考虑货运通行管制政策影响的多项Logit模型(Multinomial Logit,MNL)和巢式 Logit模型(Nested Logit,NL)，探究货运通行政策变化对各车型分担率的影响，并为改善“客车载货”现象提出对策建议.

1 数据来源和统计分析

1.1 数据来源

本文以限行时段进入市中心配送的货运出行链为研究对象，货运出行链是指货车为完成1项或几项配送任务，从出发点开始，按一定时间顺序到达不同目的点，最后返回出发点的1条活动链[8].数据来源于上海市第5次综合交通调查及课题组后续对载货面包车的补充调查，共计394条出行链数据.

参考上海市运管处普通货车车型划分标准，以车辆载重为依据，将货车车型划分为小型货车(≤2 t)、中型货车(2～4 t)、大型货车(4～8 t)和重型货车(＞8 t).同时，纳入面包车以分析通行政策对“客车载货”行为的影响.

1.2 统计分析

对样本数据中分车型的各属性特征值进行统计分析，结果如图1所示.其中，配送成本是指车辆完成1条出行链所产生的费用，考虑到数据的可获性，本文仅以燃油费表征.由于面包车载货属于违章行为，本文在面包车配送成本中加入惩罚成本0①定义为惩罚频率与惩罚金额相乘.基于既有交通法规，惩罚金额为200元/次；通过实地调研，设定惩罚频率为10%.；配送时间是指车辆完成1条出行链所耗费的总时间；通行证满足度为企业通行证拥有量与企业在限行时段进市中心配送的出行链数之比，通行证拥有量以企业货车拥有量的5%测算.

2 模型构建与参数估计

2.1 模型理论

基于随机效用最大化理论的离散选择模型，认为决策者(即配送企业)面对效用具有差异性的各备选车型，会根据认知选择能够最大程度满足其需求的车型.因此，假设决策者n的备选车型集合为An，车型i对决策者n的效用为Uin，则决策者n选择车型i的条件为

Uin可以表示为可观测的确定项Vin和不可观测的随机项εin之和，即

因此，决策者n选择车型i的概率Pin为

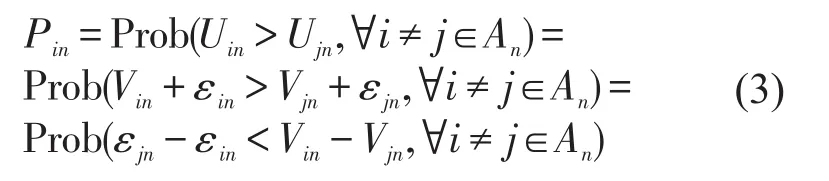
Logit模型是基于εin服从二重指数分布的假设下推导得到，包括MNL模型和NL模型等.其中，MNL模型应用最为广泛，其优点在于模型结构简单，参数估计方法成熟.MNL模型假设各备选方案的εin服从独立同分布，其概率计算公式为

图1 分车型的属性特征箱型图Fig.1 Box chart of each attributes dividing by vehicle type

εin独立同分布的假设使得MNL模型要求各备选方案独立不相关(Independence of Irrelevant Alternatives,IIA)，故MNL模型无法刻画备选方案之间的关联性.

NL模型在一定程度上克服MNL模型的IIA特性，它将备选方案相似或相关的变量纳入到1个“巢”中，允许每个“巢”内的备选方案之间具有相关性，而不同“巢”之间的备选方案相互独立.其概率计算公式为

式中：Bk为巢；K为巢的个数；λk为测度系数，反映每个“巢”k内各备选方案的相关程度，0＜λk＜1.λk越接近0，相关性越大；越接近1，相关性越小；当λ1=λ2=…=λk=1时，模型退化为MNL模型；同时，λk估计值的显著性程度体现NL模型在案例中的适用性.

考虑到实际车型选择中，某2种或2种以上车型之间可能存在相关性，本文分别建立MNL模型和NL模型，并比选较优模型，应用于后续政策评估.

2.2 模型构建

根据前文所述，本文拟选取变量如表1所示.

表1 影响因素及其参数Table 1 Influence factors and their parameters

考虑到实际情况中，单位装载率的变化对不同车型选择效用的影响不同，故将βl设为选择项特定参数，即不同车型的βl不同.而βc和βt设为通用参数(Generic Parameters)，即不同车型的该参数均相同.据此，构建初始效用函数为

式中：ASCin为待估计常数项.

应用NLOGIT软件进行初始模型的参数估计，对初始模型中参数不显著的变量逐步删除.以变量删除前后的似然比指标是否超过卡方分布临界值(如式(7)所示)为依据[9-10]，若未超过临界值，说明删除变量对模型并无显著影响.确定最终模型的变量筛选结果如表2所示.

式中：LLbase、LLnew分别为变量删除前、后的似然值；k为删除变量后待估计参数的数量.

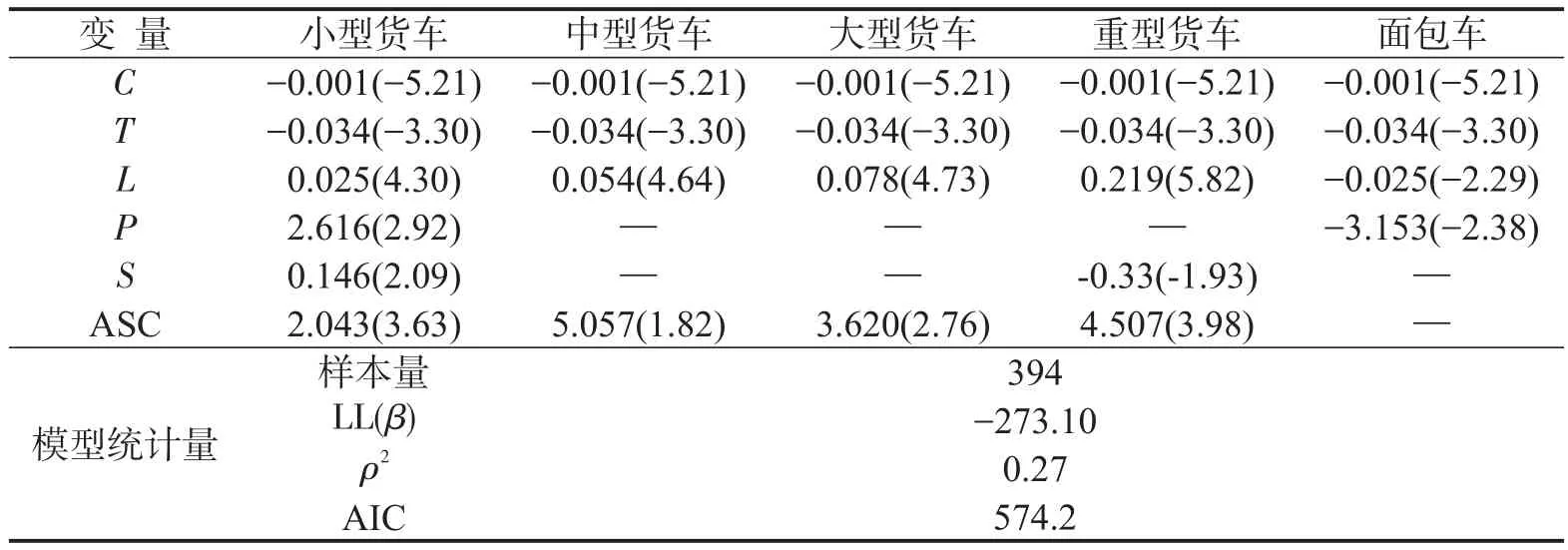
表2 MNL模型变量筛选结果Table 2 Variable selection results of MNL model

考虑到小型货车和面包车具有较强的可替代性，MNL模型假设两者的不可观测效用项独立同分布未必合理.故尝试将小型货车和面包车放入名为“轻型车”的巢中，将中型货车、大型货车和重型货车视为退化枝方案，构建NL模型，树形结构如图2所示.

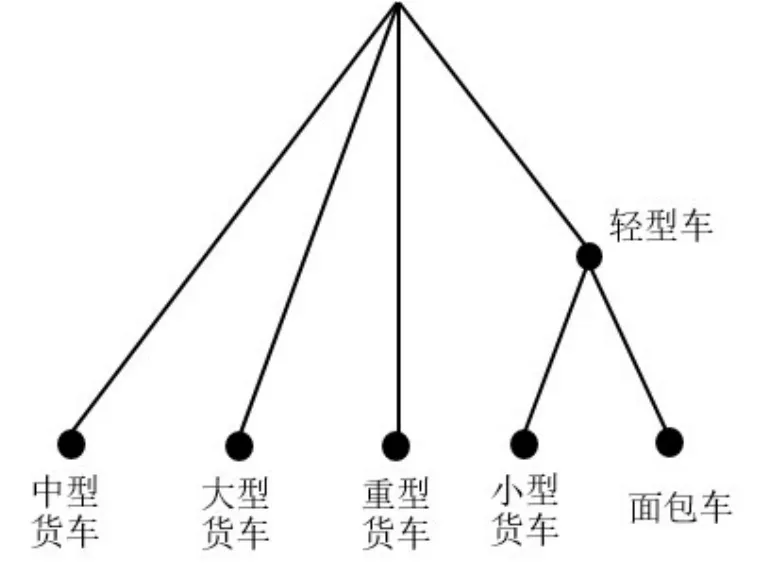
图2 NL模型树形结构图Fig.2 Tree structure of NL model

根据表2的变量筛选结果，MNL模型和NL模型的最终效用函数为

式中：s，m，l，h，c分别代表小型货车、中型货车、大型货车、重型货车和面包车.

2.3 参数估计结果

应用NLOGIT软件估计NL模型参数，结果如表3所示.从表3可以看出，测度系数λ的估计值为0.199，说明巢内的小型货车与面包车之间具有较高的相关性.由于λ反映每个“巢”k内各备选方案的相关程度，若λ=0或λ=1，均说明没有必要构建NL模型.因此，λ的t检验在于确定其是否显著不等于0，其次还需要对λ进行Wald检验，以确定其是否显著不等于1，Wald检验值的计算公式为[9-10]

式中：SD为测度系数λ的标准差；WT为Wald检验值.

式(9)中，SD的值为0.108，则Wald检验值为-7.42，大于显著水平为0.05时的临界值1.96，说明λ显著不等于1，即小型货车与面包车之间具有显著相关性，有必要构建NL模型.同时，λ的t检验值为1.84，大于显著水平为0.10时的临界值1.64，说明λ显著不等于0，有必要构建NL模型.

对比表2和表3，两类模型的Mcfadden系数ρ2均大于0.2，表明两类模型均能较好的解释车型选择行为.而NL模型的ρ2(0.30)显著大于MNL模型的ρ2(0.27)，同时，NL模型的AIC指标(557.14)小于MNL模型，均说明NL模型优于MNL模型.因此， 下文对NL模型进一步分析.

表3 NL模型参数估计结果Table 3 Parameter estimation results of NL model

从变量的影响来看，配送方式属性特征变量(包括配送成本、配送时间、装载率)对车型选择均有显著影响.其中，配送成本和配送时间的值越大，选择方案的效用值越小.而装载率越高，选择方案的效用值越大.同时，选择重型货车配送时，企业对装载率的变化最为敏感，选择小型货车配送时，企业对装载率的变化最不敏感.配送企业属性变量P对车型选择的影响表现为：随着通行证满足度的提升，企业更倾向于选择小型货车配送，而降低面包车的选择概率.出行链属性变量S的影响则表现为：随着配送点数的增加，企业更倾向于选择小型货车配送，而降低重型车的选择概率.

3 货运政策对车型分担率的影响评估

引起“客车载货”现象的主要原因是：一方面在于企业日间配送中通行证得不到满足，另一方面为面包车购置成本、配送成本相对低廉.通过上述模型验证，通行证满足度、配送成本均对货车车型选择具有显著影响.为进一步分析上述变量对车型分担率的具体影响，依据NL模型的参数估计结果，模拟不同通行证发放比例(当前为5%)和“客载货”惩罚成本(当前为20元)下的面包车分担率变化趋势，这里面包车分担率是指面包车出行链量占出行链总量的比率.模拟结果如图3所示.

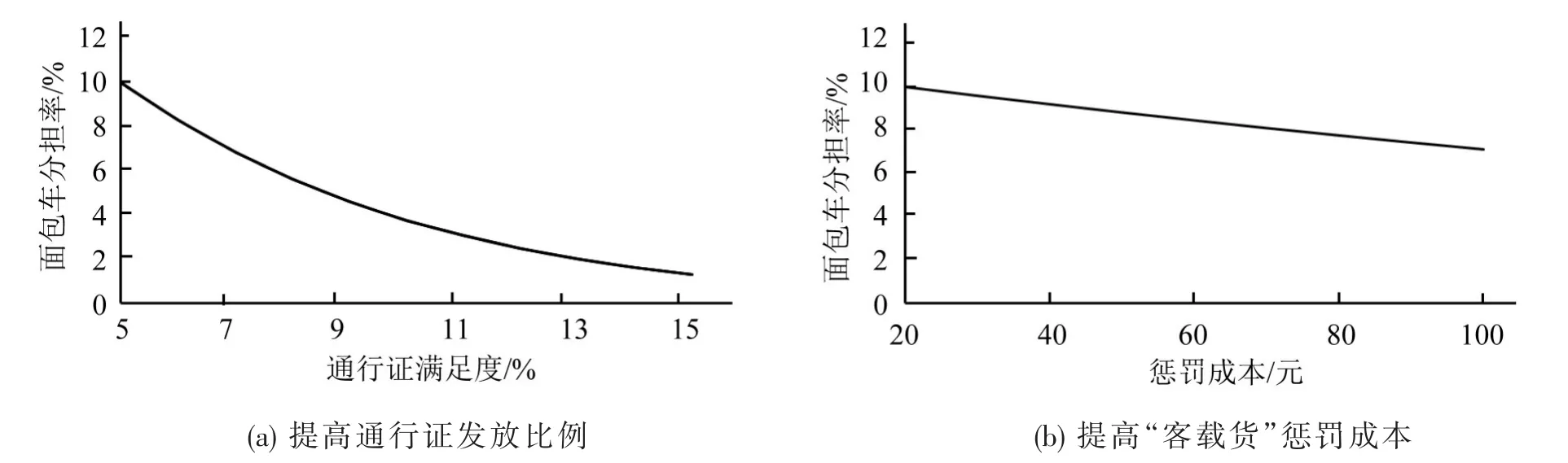
图3 通行措施变化对面包车分担率的影响Fig.3 The impact of the change in the passing policies to the share rate of the seven-seat car

从图3可知，提高通行证发放比例和“客载货”惩罚成本均可降低面包车分担率.进一步来看，由分担率曲线斜率可知，通行证发放比例对面包车分担率的影响远大于“客载货”惩罚成本，即同比例的通行证发放比例增加所引起的面包车分担率减少远大于通过提高“客载货”惩罚成本所带来的面包车分担率减少量.具体来看，当通行证的发放比例提升50%，即由当前的5%升至7.5%时，面包车的分担率由10.11%减少至6.30%；而当“客载货”惩罚成本提高50%时，面包车的分担率仅降至9.69%.

结合调研情况和可实施性，建议近期对通行措施进行如下调整：通行证发放比例由当前的5%提高至7.5%；同时，通过加大执法力度，使得“客载货”行为惩罚频率由当前的10%增至50%.经模型测算，调整前后的各车型分担率如表4所示.从表4可以看出，调整后面包车出行将大部分转移至小型货车，其分担率可降至4.4%.此外，对于不同配送点数的出行链，面包车所占比例有所不同，其分担率随着配送点数的增加而下降；且在建议措施下，对于不同配送点数的面包车出行链，其分担率转移量具有差异性，如表5所示.

与仅提升通行证发放比例至7.5%相比，建议措施能够使面包车出行分担率实现大幅度下降，说明提高通行证发放比例的同时进一步增加“客载货”惩罚成本可有效降低面包车载货出行.原因在于尽管企业通行证满足度得以提升，面包车自身具有配送成本低、通行机动灵活等优势，能够方便地进入高架道路、隧道等货车限行区，且可进入因出入口限高货车无法进入的停车场(库).因此，在逐步提高通行证发放力度的同时需要加大对面包车的惩罚力度.

表4 建议措施下的各种车型分担率Table 4 Share rates of each vehicle type under suggestions

表5 不同配送点数的出行链在建议措施下的面包车分担率Table 5 Share rates of vehicle type of the tours with different number of stops under suggestions(%)

基于上述分析，近期建议通过采取如下措施以改善“客车载货”现象：

①建议相关政府部门逐步提高通行证发放比例.同时，考虑到目前通行证在发放上过于硬化，建议调研各配送企业的实际配送需求，按照“专业运输优于非专业运输，城市配送优于普通货运”的原则给予重点配送企业一定的发放政策倾斜.

②建议相关政府部门加大查处面包车载货行为的执法力度，进一步杜绝因其车型优势而产生的载货行为.

③建议研发可替代面包车的城市配送专用车型，鼓励企业更换并给予一定的补贴支持及通行优待.

④对于有较大货运需求且配套停车场(库)出入口高度不满足货车进入的公共建筑，建议在交警部门和交通部门的核定下，可根据实际路况在附近道路划定停车位和装卸区，允许货运车辆在非高峰时段停靠和装卸货物.

4 结论

特大城市中普遍存在的“客车载货”现象制约了城市交通的可持续发展，为科学评估城市货运通行管制政策，本文以限行时段进入市中心配送的货车出行链为研究对象，在考虑配送方式属性、出行链属性和配送企业属性3方面影响因素的基础上，构建包含小型货车、中型货车、大型货车、重型货车和面包车5种车型的城市货运车型选择的MNL模型和NL模型.结果表明配送成本、配送时间、装载率、配送点数和通行证满足度对城市货运车型选择影响显著.经模型比选，应用较优的NL模型模拟通行证发放比例和“客车载货”行为惩罚成本的变化对面包车分担率的影响，结果表明通行证发放比例对面包车分担率的影响远大于“客载货”惩罚成本.其次，测算货运通行措施调整建议下各车型的分担率，结果表明该建议有效促使面包车的配送出行向小型货车转移，且针对不同配送点数的出行链，面包车配送出行的转移量具有显著差异.最后，本文提出了改善“客车载货”现象的相关对策.

然而，以下问题仍有待进一步研究：①考虑到本文仅采用RP(Revealed Reference)数据，存在变量变化很小或共线性等问题，未来有必要采用RP/SP(Stated Preference)数据融合，从而提高模型的解释能力；②可进一步从货车流量、车公里、尾气排放量等指标评估城市货运管理政策.