一种便于培育家庭农场的规划模型构建与应用

王树进， 刘 昭

(南京农业大学经济管理学院，江苏南京 210095)

1 研究背景

1.1 农业供给侧结构性改革与家庭农场

推进农业供给侧结构性改革，是加快转变农业发展方式的重要途径[1]。我国不同农产品面临着阶段性供过于求与供给不足并存的局面，推行农业供给侧改革，不能单纯追求农产品产量的增长，也不能只从国内市场供求的视角对现有各类农产品进行生产结构上的调整，而是要在经济全球化的背景下，深入思考如何在总体上提高我国农业的综合效益和国际竞争力[2]。农业供给侧结构性改革的重点主要在3个方面：一是去库存，即加快消化过大的农产品库存量；二是降成本，通过发展适度规模经营和社会化服务等，优化全产业链的分工来扩大农业效益，降低生产成本和提高竞争力；三是补短板，加强农业基础设施等薄弱环节的建设，增加市场紧缺农产品的生产[3]。

家庭农场是发展农业适度规模经营最重要的主体，也是未来农业社会化服务的主要对象。不同国家对家庭农场的概念不尽相同。美国农业部将家庭农场定义为在某一年通常生产和销售至少1 000美元农产品的场所[4]。我国对家庭农场的通常定义为，以家庭成员为主要劳动力，从事农业规模化、集约化、商品化生产经营，并以农业收入为家庭主要收入来源的新型农业经营主体。家庭农场这样的农业经营主体，其内涵必然表现为以农户为经营主体，以适度规模为经营方式，以利润最大化为生产目标[5]。而要实现利润极大化，经营主体就必然要面向市场，生产市场紧缺的农产品。因此，发展家庭农场，去库存、降成本、补短板这3个目标可同时得以兼顾。

纵观世界发达国家的农业组织形式，无论其规模大小和类型如何变化，家庭经营都是最基本的组织形式[6]。家庭农场因其经营产品的种类不同，可以分为多种类型，如粮油、蔬菜、花卉、林果、中药材种植和畜禽水产的养殖等。不同类型的农场，其合理的投资规模与资源占用量也有较大差异[7]。未来一个地区的农业经济总量，可认为是其域内全部家庭农场经营活动的总和。因此，从面向未来的农业规划的视角来看，无论是一个园区、一个村、一个镇、一个县，还是更大区域内的农业供给侧的结构与规模，都可以用该区域各类家庭农场的数量来描述。因而，本研究以家庭农场为规划模型中的决策变量。

1.2 农业规划模型的基本假设

农业规划是指对一定区域范围未来一段时期农业发展、农业资源开发和生产力布局所作的总体部署，是目标与约束、组织与过程的综合体[8]。农业规划是一个广泛的管理领域，包括农业经济的重大问题，如土地分配与再分配、灌溉、种植模式设计、机器时间分配等[9]。目前，农业规划中被高频采用且比较有效的技术方法主要有线性规划法、比较优势法、态势分析法(SWOT)和3S技术等4类[10]。其中线性规划法使用最普遍，建立农业规划模型的技术门槛最高，假设条件也更为明确。自从20世纪80年代初以来，线性规划方法便广泛应用于农业规划。Fokkens等于1981年引入线性规划(linear programming，简称LP)模型作为大型粮食农场管理收割工作的工具[11]。Monaco等运用线性规划模型优化配置农业资源，协调农业生产活动与区域食品需求[12]。本研究采用线性规划法，模型构建基于以下三大假设。

一是理性经济人假设。假设规划区内的农业经营主体由家庭农场和龙头企业(或合作社)构成，二者都是以利益极大化为经营目标的经济人。具体分工是：家庭农场负责农业生产，企业(合作社)负责产品销售、品牌经营、生产组织、质量控制与计划管理。规划以家庭农场纯收入总和的极大值为目标。家庭农场与企业(合作社)之间的产品结算价格以计划合同来约定，不同类型的家庭农场单体规模，原则上以纯收入不低于20万元/年和用工量不高于1 000工日/年这2个标准来确定，前者保证家庭农场对青年才俊有一定的吸引力，后者保证家庭农场符合以家庭成员为主要劳动力的属性要求。在纯收入计算时采用上述结算价格。纯收入一般指从农业收入中扣除农业物质耗费后的农业增加值。对于家庭农场而言，家庭纯收入除了从农业销售总收入中扣除物质耗费以外，还应扣除土地租金和雇工费。家庭成员(如一对夫妇)的劳动成本不扣除。

二是资源假设。农业资源是农业发展的重要物质基础，主要包括自然资源(土地、水、气候、生物等)、人工物化资源(肥料、农药、种子等)、人力资源、资本资源、信息资源等[13]。农业生产对自然资源和环境的依赖性极强，农业资源禀赋条件决定着农业发展的水平和潜力。因此，农业规划必然是在有限的资源约束下进行的。本研究主要考虑农用地、设施农业用地、可养殖水面、水资源、劳动力、投资、流动资金这7种农业资源的可获量。每种资源以1个约束方程来表示，规划区内各家庭农场对每类资源消耗量之和不得超过该项资源可获量。

三是任务假设。农业规划既受到客观的农业资源约束，也受到主观的任务约束。我国农业实际上需要承担起粮食安全、食品安全以及一定程度的就业保障这3个功能[14]。粮食安全要求农业生产满足消费者对以粮食为主的农产品的数量需求，食品安全则是对农产品质量的要求。一些企业主办农业园区，其重要动因就是要生产一定数量的能满足本企业员工生活需要的高品质农产品，以此提高企业员工福利；而乡村集体组织和农村基层政府，则往往希望通过发展现代农业能为农村劳动力提供一定的就业岗位。据此，本研究假设任务约束包括生产约束与就业约束两大类：生产任务是对各种农产品生产数量的约束，就业约束指规划区内农业生产需要提供的最少就业岗位数。

2 模型设计

2.1 优化模块

鉴于上述分析，本研究以家庭农场的种类与数量为决策变量，以各家庭农场纯收入之和为目标函数，考虑土地、资金、劳动力等客观资源限制，以及就业、粮油、蔬菜、肉制品等任务目标等约束条件，构建了农业规划模型，优化模块如下：

(1)

2.2 输入模块

输入模块分为3个部分，第一部分是目标函数中的效益系数，即向量C，代表每个不同类型的家庭农场年度纯收入情况，这部分数据受农产品市场行情影响较大；第二部分是技术系数矩阵，即A，反映不同类型的家庭农场对各种资源的耗费以及对任务的贡献，这部分数据受技术进步的影响较大；第三部分是规划区域自身的资源禀赋与任务要求，即B，这部分数据通过对规划区域以及规划实施单位的调查获得。

2.2.1 效益系数向量CC是n维向量，C=(c1，c2，…，cn)。cj(j=1，2，…n)的表达式如下：

(5)

式中：qjk代表第j类家庭农场生产的第k种农产品的产量，k=1，2，…，L；pjk代表第j类家庭农场生产的第k种农产品的结算价格，k=1，2，…，L；sj代表第j类家庭农场的生产成本。

生产成本是农产品生产过程中耗费的全部物质费用和人工费用，人工费用即雇工费，不包括含家庭成员的劳动成本。生产成本包括直接费用如肥料、农药、农膜、其他消耗品、水费、电费、农事外包费、雇工费，以及间接费用如初始投资分摊、贷款利息与保险费、土地租赁费、销售费用等。

2.2.2 技术系数矩阵A家庭农场有n类，资源与任务约束有m项，用aij代表第j类家庭农场对第i种资源的需求量或对第i种任务的贡献量，则技术系数矩阵A可以用下式表达：

(6)

式中：技术系数的变化取决于家庭农场主对农业新技术的采用情况。一般来说，技术系数的变化周期比市场行情的变化周期要长得多，所以相对于效益系数向量C，技术系数矩阵A可在较长时期内保持稳定。

2.2.3 资源或任务约束向量BB是规划模型的右边项(常数项)，它代表具体规划实施主体的资源可获量和任务要求，构成了规划系统中约束条件的上限和下限。其表达式如下：

B=(b1，b2，…，bt，bt+1，…，bm)T。

(7)

式中：(b1，b2，…，bt)为资源可获量上限，(bt+1，…，bm)为任务要求的下限。

2.3 输出模块

输出模块主要包括决策方案、影子价格、产品一览表3个部分。

2.3.1 决策方案 决策方案即决策向量，是对规划区域内各类家庭农场发展的数量，具体数值用分量xj表示。

X=(x1，x2，…，xn)T。

(8)

式中：xj代表规划区域内第j类家庭农场的数量，j=1，2，…，n。本研究采用科学出版社《家庭农场模型设计与评价》一书中的家庭农场精选模型作为决策变量，n为42个，其中包括粮油种植类5个、蔬菜种植类10个、花卉林果种植类9个、中药材种植类7个、动物养殖类10个。

2.3.2 影子价格 影子价格指某种资源在生产活动中的边际利用价值，在数值上等于每增加1个单位资源所带来的边际收益，它反映了资源的稀缺程度。影子价格越大，表示这种资源的实际价值越高，越趋于紧缺。影子价格为0则表示这种资源不紧缺。

影子价格作为输出模块，对农业规划决策具有重要的参考价值，有助于科学制定实施规划的延伸方案。

2.3.3 产品一览表 产品一览表呈现的是规划区域内生产的农产品种类和数量，反映了实施规划后农产品的结构和规模。产品的种类和数量用向量Q表示，表达式如下：

Q=(q1，q2，…，qL)；

(9)

(10)

式中：qk代表规划区域生产的第k类农产品的产量，k=1，2，…，L；xj代表规划区域内第j类家庭农场的数量，j=1，2，…，n；qjk代表规划区域内第j类家庭农场生产的第k类农产品的产量。

4 模型应用案例

4.1 案例来源与数据输入

S公司是全国著名的上市公司，拟在苏北某地流转一片农地创建现代农业产业园，其目的一是生产优质安全蔬菜以及其他农产品以满足公司内部食堂的需求，二是进军农业领域，为公司未来发展探索新的增长点。该企业可以获得的各项资源和满足内需的任务要求详见表1。

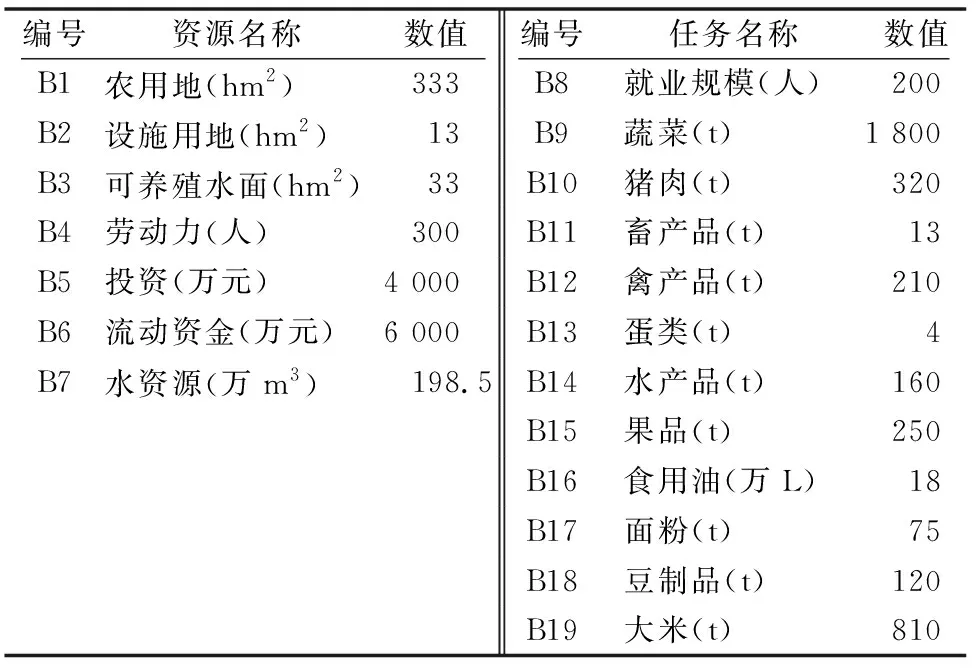
表1 S企业园区的资源与任务约束

注：数据来源于对项目区的实地调研数据。其中，B7水资源根据公式“可灌溉水资源总量=水库/池塘面积×(年降水量-水面年蒸发量)+其他汇水面积×年降水量×径流系数”测算。

4.2 规划结果的讨论

将表1中的数据输入到本研究构建的规划模型中，可以得出该公司现代农业产业园的规划方案如下。

4.2.1 家庭农场的种类与数量 家庭农场的种类与数量即模型输出的决策变量xj的数值(表2)。该方案下的园区应发展11类家庭种植园，6类家庭养殖场。该方案下，园区家庭农场的纯收入之和为 3 704.38 万元。

表2 S公司农业园区的规划方案

4.2.2 规划区的农产品种类与数量 在上述方案下，园区生产的产品种类与数量如表3所示。

4.2.3 影子价格分析 模型输出规划方案下的影子价格如表4所示。从表4可以看出，资源约束中，农用地、劳动力资源、投资的影子价格不为0，表明这3种资源对于园区是紧缺的；而设施用地、可养殖水面、流动资金、水资源的影子价格为0，存在资源剩余。在其他条件不变的情况下，若紧缺资源影子价格大于该种资源的获取成本，则进一步扩大该资源的投入是有利可图的。以农用地为例，农用地资源的影子价格为2.1万元，表示每增加1 hm2农用地，纯收入将增加2.1万元。在当前的状态下，如果按1.5万元/hm2流转费用计算，增加农用地流转规模带来的边际收益大于边际成本，总收益增加。在任务约束中，蔬菜、禽产品、蛋类、食用油、豆制品、大米的影子价格为负，表示这些任务约束如果能够降低的话，园区的纯收入将会增加。

表3 产品一览表

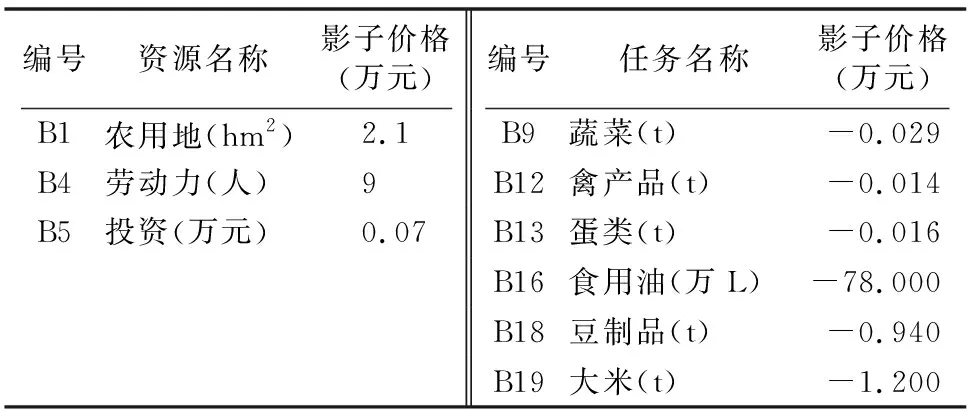
表4 规划方案下的非零影子价格

4.2.4 与原规划方案的比较分析 在应用本模型之前，S公司的规划项目团队凭经验对该园区进行了规划，总共占用农地519.593 hm2，全年纯收入总和为3 739万元，平均纯收入7.2万元/hm2；应用本模型后，占用土地面积333.500 hm2，全年纯收入总和为3 704万元，平均纯收入11.1万元/hm2。相比之下，应用本模型得出的优化方案与原方案相比，单位面积纯收入增加了54.17%。

4.2.5 最佳投资规模模拟 本模型还可以用来模拟资源的最佳投入规模。以投资规模为例，假定其他资源与任务要求都不变，仅改变投资额，得到总收益与投资额之间的关系如图1所示。图1中的总收益即纯收入之和。随着投资额的增加，总收益呈先增后减的规律，约在投资额4 600万元处园区取得最大总收益，这与边际报酬理论的解释高度一致。根据边际报酬理论，一个生产系统每增加一个单位投资，就要付出一定的资金成本(如贷款利息)，但系统的总收益达到一定阶段之后会遵循报酬递减规律，当边际报酬等于边际成本时，总收益曲线一定会出现顶点，本案例验证了这一规律。通过模型模拟得出了总收益的顶点，对应的投资额(4 600万元)就是现有土地、劳动力等生产要素约束下的最佳投资规模。