学会知识迁移 提高解题能力

王晓东

波利亚认为：“中学数学教学的首要任务就在于加强解题能力的训练。”对于初三数学总复习时出现的题目，大都具有一定的综合性，覆盖多个知识点，因此，学生除了具备比较扎实的各部分基础知识外，由此及彼，由表及里，把未知问题转化为已知问题，利用知识迁移解决问题是有效的途径。下面是我对几个问题的处理方法：

问题1：有一个运算程序，可以使：a ⊕ b=n（n为常数）时，得（a+1）⊕b=n+1，a ⊕（b+1）=n-2，现在已知：1 ⊕1=2，那么，2010 ⊕ 2010=_。这个问题看似简单，但全班同学反复读题后无从下手，学生已山穷水尽，渴望得到帮助。于是我设计了以下两个问题，以此启发学生的思考。

①同学们想一想，（a+1）⊕b，a ⊕（b+1）与a⊕b有关系吗？学生通过观察思考、讨论交流，便回答：（a+1）⊕b=a⊕b+1，a ⊕（b+1）= a⊕b-2.

②已知条件是1 ⊕1=2，我们设想能不能用大家刚才想到的关系式，把2010 ⊕ 2010最终与1 ⊕1联系起来，从而获得结果呢？同学们思考、讨论、交流，开始大胆尝试如下：

2010 ⊕ 2010

=（2009+1）⊕ 2010

=2009 ⊕ 2010+1

=2008⊕ 2010+2

=……

=1⊕ 2010+2009

=1⊕（2009+1）+2009

=1⊕ 2009-2+2009

=1⊕ 2008-4+2009

=……

=1 ⊕1-2×2009+2009

=2-2009

=-2007.

通过本题的解答，学生对这种由知识间的内在联系而产生的问题，有了一定的把握。通过经历独立思考与合作交流的解题过程，既掌握了知识，也培养了学生的数学运算素养和逻辑推理素养。

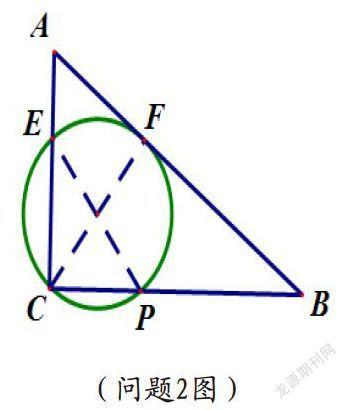
问题2：如图，在RtΔABC中，∠ACB=90°，AC=6，BC=8，过点C的圆与AB相切，交AC于E，交BC于点P，则PE的最小值是_。

这道题看似无从下手，PE何时为最小，我这样引导学生仔细分析，经过点C且与AB相切的圆，交AC于E，交BC于点P，会想到，这个圆的直径就是RtΔABC中AB边上的高，于是作CF⊥AB与F，以CF为直径作圆，分别交AC、BC于E、P。因为∠ACB=90°，所以PE为圆的直径，所以PE=CF，由于CF最小，所以PE便最小，故PE的最小值是6×8/10=4.8.

（问题2图）

本题也是把点到直线的距离最小迁移到这一问题中从而使问题获得解决。苏联著名心理学家鲁宾斯坦强调，概括是迁移的基础。他认为，在解决问题时，为了实现迁移，必须把新旧课题联系起来并包括在统一的分析综合活动中。

通过这两个题的解题过程的分析、思考，锻炼了学生的思维素养，拓展了学生的思维空间，培养了学生良好的思维品质，提升了学生的解题能力，也培养了学生的数学建模素养和逻辑推理素养。当代教育家窦桂梅说“自己发现的东西才最有价值。”

问题3 如图，已知二次函数y=ax?+bx+c的图像与x轴交于（x1，0）（x2，0）两点且0﹤x1﹤1，1﹤x2﹤2，与y轴交于（0，-2），下列结论：①2a+b>1，

②3a+b>0，③a+b﹤2，④a﹤-1.

其中正确结论的个数为（ ）

A 1 B 2 C 3 D 4.

（问题3图）

引导学生进行思路分析：①由图可知，c=-2，若2a+b>1成立，则2a+b-1>0成立，即4a+2b-2>0成立，对照函数解析式，它表示x=2时，y>0，从图像上看，此时y﹤0，因此错误。

②由图可知，当x=1时，y>0，x=2时，y﹤0所以，

解这个不等式组得，3a+b﹤0，结论②显然错误。

③若a+b﹤2成立，即a+b-2﹤0 成立，也就是当x=1时，y﹤0，由图像可知，此时y>0，故结论③不成立。

④由

得2a+2﹤0，所以，a﹤-1正确。

通过观察函数图像位置，确定函数值的正负性，构造不等式组，是解决二次函数系数关系的重要方法。本题把不等式、不等式组的知识迁移到解决二次函数系数关系问題中，这种方法是解决二次函数问题的一般方法。

奥苏贝尔认为，在有意义学习中，认知结构始终是一个关键的因素，现有的学习受原有认知结构的影响，原有的认知结构由于接收新信息而得到改造，这种改造后的认知结构又会影响后继的学习。

掌握了思维方法，把复杂问题浅显化，学生就能学会学习、会解决问题，实际上这也是一种能力，有了这种能力就会明显地促进正迁移。学生的直观想象素养和数学运算素养得到了提升。

参考文献

[1]中学数学教学参考2017年 第 12期 65页

[2]《当代教育家教育智慧》范晓红编 2011年7月 第174页