装配式U形混凝土渠道衬砌钢模具数值模拟

程传胜 田军仓 王斌 王馨苑

摘要：为了探求装配式U形混凝土衬砌渠道钢模具在预制混凝土衬砌板时的应力应变规律，2A D60装配式U形混凝土渠道衬砌钢模具为研究对象，运用ADINA软件对不同厚度、不同纵向加劲肋及不同横向加劲肋的钢模具进行数值模拟。结果表明：钢模具的变形在直线段最大，弧线段次之，直线连接段和弧线连接段最小；等效应力在直线连接段和弧线连接段最大，直线段和弧线段较小，并且钢模具厚度的影响程度>纵向加劲肋数量的影响程度>横向加劲肋数量的影响程度；在一定的变形允许范围之内，装配式U形混凝土衬砌渠道钢模具的厚度以8-10～为宜，纵向加劲肋以3-4根为宜，横向加劲肋以2根为宜（布置在直线段和弧线段各1根）。

关键词：U形混凝土衬砌渠道；钢模具；数值模拟；应力应变；ADINA

中图分类号：TV431 文献标志码：A doi：10.3969/ j.issn.1000-1379.2018.03.033

旱寒地区渠道基土在较大昼夜温差的连续作用下，冻土层不断加厚，冻胀加剧，使渠道衬砌板发生不同程度的冻胀破坏[1]。王正中等[2-3]建立了梯形和弧底梯形渠道的冻胀破坏力学模型；李学军等[4]建立了热耦合模型对U形混凝土衬砌渠道抗冻胀进行分析，认为U形渠道冻胀变形分布不均匀，弧板中部左右的冻胀变形较大；郑源等[5]建立了弧底梯形渠道衬砌的冻胀力学模型，得出弧底梯形渠道在坡脚处没有应力突变的结论，可有效改善坡脚处冻土对衬砌板的约束作用；李翠玲等[6]认为U形渠道衬砌弧板是由法向冻胀力、冻结力及切向冻结力和重力共同作用的薄壳拱形结构；闫长城等[7]通过热耦合把渠基土和衬砌板作为整体，运用有限元软件分别对混凝土和玻璃钢渠道进行了温度场、位移场和应力应变场分析，认为玻璃钢渠道可使法向冻胀力和切向冻胀力都减小，最大位移变大，但最大释放变形量也较大，且变形更加均匀；程传胜等[8]以衬砌板为研究对象，通过ADINA软件对玻璃钢和混凝土渠道进行位移场和应变场分析，得到与文献[7]相同的结论。以上研究从不同角度对渠道进行了抗冻胀分析。

对宁夏地区装配式U形混凝土渠道衬砌板的質量情况进行调研，发现装配式U形混凝土渠道衬砌板质量差异很大，其预制钢模具不统一，成型底板厚度5～12mm不等，底板的加劲肋数量和位置相差甚大，规格不统一，施工当中造成破坏也没有统一的零件进行更换维修，基本上是一次性购买与使用，加大了钢材使用量，增加了U形混凝土渠道衬砌板的成本，限制了宁夏地区高效节水技术的推广与应用。本研究针对装配式U形混凝土衬砌渠道钢模具建立不同加劲肋数量及位置和不同厚度钢模具的有限元模型，进行数值模拟分析，以期为研究装配式U形混凝土衬砌渠道提供技术支撑。

1 装配式U形混凝土衬砌渠道钢模具的有限元计算

1.1 钢模具有限元模型

为建立装配式U形混凝土衬砌渠道钢模具有限元模型库，实地测量现有D60装配式U形混凝土衬砌渠道钢模具有关参数，结合文献[8-9]，取装配式U形混凝土衬砌渠道钢模具的一半为研究对象，建立不同厚度、不同加劲肋数量及位置的钢模具有限元模型。在相同条件下，改变装配式U形混凝土衬砌渠道钢模具的厚度或加劲肋数量及位置，分析不同厚度、不同加劲肋数量及位置的钢模具应力应变分布规律及对抵抗激振力变形的影响。

1.2 钢模具模型材料及边界条件

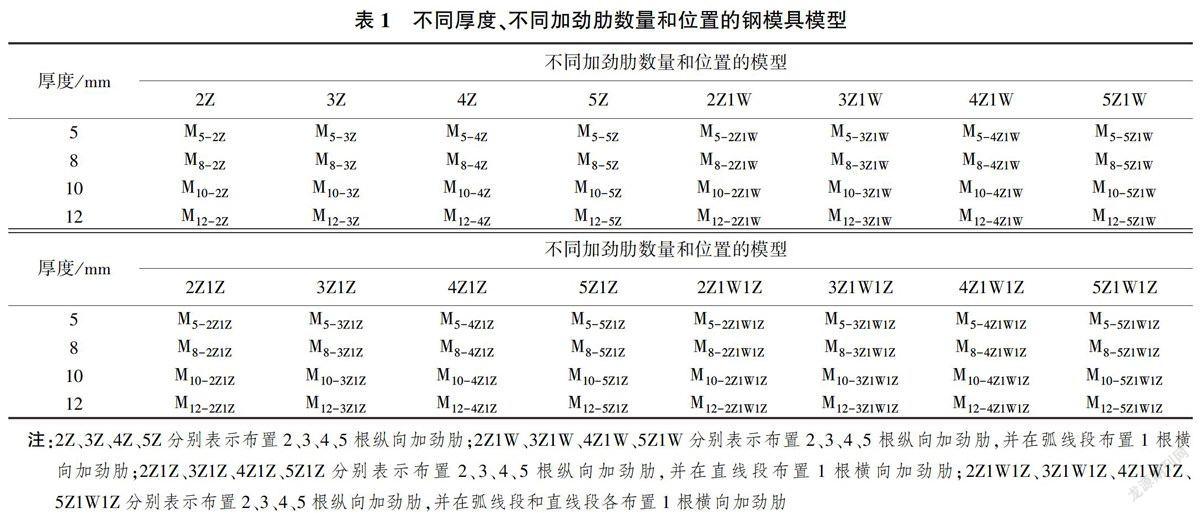
根据假设及实际装配式U形混凝土衬砌渠道钢模具的基本情况，建立厚度分别为5、8、10、12mm，加劲肋数量和位置分别为2Z、3Z、4Z、5Z、2Z1W、3Z1W、4Z1W、5Z1W、2Z1Z、3Z1Z、4Z1Z、5Z1Z、2Z1W1Z、3Z1W1Z、4Z1W1Z和5Z1W1Z，圆弧半径为300mm的装配式D60U形混凝土衬砌渠道钢模具，一共64个实体模型，具体模型见表1。

材料的本构模型对分析结果十分重要，根据前期大量的数值模拟结果，钢材的强度远远达不到其屈服强度，应力应变处于弹性阶段，所以钢材的材料本构模型采用线性弹性材料，理论基础为线弹性理论，此种模型可以模拟钢材的基本属性。本研究选用Q235钢，具体参数见表2。

本研究取钢模具约束条件为连接轴处和螺栓铰接处全部线约束，其他为自由表面。定义单元类型为3D-SOLID单元，选择8节点6面体单元进行映射划分，每个实体模型有2580个单元、3996个节点。图1是厚度为8mm、加劲肋情况为4ZIWIZ的钢模具有限元模型，相关参数与实际钢模具一致，各模型在求解时去掉X、Y、Z三个方向平动和旋转自由度，选择FullNewton Method完全牛顿迭代方法、Spare稀疏求解器、Energy能量收敛准则。

2 装配式U形混凝土衬砌渠道钢模具数值模拟结果分析

2.1 不同厚度、不同加劲肋数量和位置的钢模具变形分析

由于不同厚度钢模具的变形随不同纵向加劲肋数量、不同横向加劲肋数量及位置的变化趋势是一致的，因此绘制同一厚度（8mm）、相同横向加劲肋数量（2根）及位置、不同纵向加劲肋数量，同一厚度（8mm）、相同纵向加劲肋数量（4根）、不同横向加劲肋数量及位置，相同纵向加劲肋数量、相同横向加劲肋数量及位置、不同厚度的装配式混凝土衬砌渠道钢模具的变形图，见图2～图4。

由图2可知，厚度和横向加劲肋数量及位置一定时，随着纵向加劲肋数量的增加，钢模具变形逐渐减小，钢模具中间位置变形较大，两端变形较小。纵向加劲肋数量分别为2、3、4、5时，最大变形分别为0.231、0.043、0.032、0.024mm，纵向加劲肋数量为3的钢模具最大变形比纵向加劲肋数量为2的减小了81.39%，纵向加劲肋数量为4的钢模具最大变形比纵向加劲肋数量为3的减小了25.58%，纵向加劲肋数量为5的钢模具最大变形比纵向加劲肋为4的减小了25.00%。由此可见，纵向加劲肋数量由2到3时，钢模具变形大幅减小，纵向加劲肋数量由3到5时，其变形也在减小，但最大变形削减程度逐渐减小。

由图3可知，钢模具中间位置的变形较大，两端的变形较小，并且相对于在直线段的横向加劲肋，在弧线段的横向加劲肋的钢模具的整体变形减小，横向加劲肋分别为0、1Z、1W和1w1Z时，钢模具的最大变形分别为0.0362、0.0361、0.0342、0.0317mm，横向加劲肋为1Z的钢模具与横向加劲肋为0的钢模具相比，整体变形相差很小，横向加劲肋为1W的钢模具比横向加劲肋为1Z的钢模具最大变形减小了5.26%，横向加劲肋为1w1Z的钢模具比横向加劲肋为1W的钢模具最大变形减小了7.31%。由此可知，当横向加劲肋为1W1Z时，钢模具的最大变形最小。

由图4可知，纵向加劲肋的数量和横向加劲肋的数量及位置一定时，随着厚度的增加，钢模具的变形逐渐减小，钢模具中间位置的变形较大，两端的变形较小。厚度分别为5、8、10、12mm时，钢模具的最大变形分别为0.0564、0.0317、0.0265、0.0218mm，厚度为8mm的钢模具比厚度为5mm的钢模具最大变形减小了43.79%，并且钢模具的整体变形相对均匀；厚度为10mm的钢模具比厚度为8mm的钢模具最大变形减小了16.40%，厚度为12mm的钢模具比厚度为10mm的钢模具最大变形减小了17.74%。钢模具的整体变形随着厚度的增大而减小，但厚度为12mm时，厚度对钢模具的整体变形削减程度变化不大。

2.2 不同厚度、不同加劲肋数量和位置的钢模具应力

场分析

由于不同厚度钢模具的等效应力随不同纵向加劲肋数量、不同横向加劲肋数量及位置的变化趋势是一致的，因此本文列出同一厚度（8mm）、相同横向加劲肋数量（2根）及位置、不同纵向加劲肋数量，同一厚度（8mm）、相同纵向加劲肋数量（4根）、不同横向加劲肋数量及位置，相同纵向加劲肋数量、相同横向加劲肋数量及位置、不同厚度的装配式混凝土衬砌渠道钢模具的等效应力分布图，见图5～图7。

由图5可知，在厚度和横向加劲肋一定时，纵向加劲肋数量由2至5增加的过程中，钢模具的等效应力逐渐减小，其中：由2至3变化时，钢模具的等效应力大大减小；由3至5变化时，其等效应力减小，但减小幅度也在变小，在钢模具的中间部位其等效应力几乎没有变化。当纵向加劲肋的数量为2时，弧线段端部的等效应力为9.38～16.10MPa，弧线段的等效应力为7.55～15.40MPa，直线段的等效应力为4.20～7.59MPa，直线段端部的等效应力为4.98～8.95MPa；而纵向加劲肋数量为3时，弧线段端部的等效应力为0.36～2.01MPa，最大等效应力减小了87.52%，弧线段的等效应力为0.74～2.89MPa，最大等效应力减小了81.23%，直线段的等效应力为0.74～3.05MPa，最大等效应力减小了89.82%，直线段端部的等效应力为1.10～4.39MPa，最大等效应力减小了 50.95%，大大削减了钢模具的等效应力。在纵向加劲肋数量由3至5时，各段的等效应力随着纵向加劲肋的数量的增加逐渐减小，但变化幅度很小，此时纵向加劲肋的数量增加对钢模具的等效应力影响程度较小。

由图6可知，钢模具中间位置的等效应力较小，两端的等效应力较大，直线段的横向加劲肋和在弧线段的横向加劲肋的钢模具的整体等效应力相差不大；横向无加劲肋时，钢模具横断面各点的等效应力相对较小，但其不均匀度较大，直线连接段端部的等效应力为1.04～4.92MPa，直线连接段的等效应力为1.21～1.81MPa，直线段的等效应力为0.461～2.08MPa，弧线段的等效应力为0.877～2.08MPa，弧线段端部等效应力为0.877～3.12MPa，分布极不均匀，这大大限制了钢模具在施工中的应用；横向加劲肋数量为2（1W1Z）时，即直线和弧线段分别布置横向加劲肋时，钢模具的等效应力较小，直线连接段端部最大等效应力为3.97MPa，减小了19.31%，直线连接段的最大等效应力为2.49MPa，增加了37.57%，直线段的最大等效应力为2.29MPa，增加了10.10%，弧线段的最大等效应力为2.08MPa，几乎没有变化，弧线段端部最大等效应力为1.92MPa，减小了38.46%，与其他横向加劲肋布置情况相比，直线段和弧线段分别布置横向加劲肋的钢模具大大降低了两端的最大等效应力，钢模具等效应力分布也较为均匀。

由图7可知，厚度为5mm时，钢模具的整体等效应力很大，直线连接段端部、直线连接段、直线段、弧線段、弧线段端部的最大等效应力分别为10.10、3.64、4.41、2.62、5.79MPa，等效应力分布不均匀；厚度为8mm时，其整体等效应力较厚度为5 mm时大为减小，直线连接段端部、直线连接段、直线段、弧线段、弧线段端部的最大等效应力分别为3.97、2.49、2.29、2.10、1.92MPa，分别减小了60.69%、31.59%、48.07%、19.85%、66.84%，大大减小了各部位的等效应力峰值，分布较均匀；在厚度由8mm至12mm变化时，其整体等效应力减小，但厚度的增加对钢模具的变形削减程度不大，其等效应力曲线几乎重合，仅仅表现在两端位置的等效应力的削减程度不同。

2.3 不同厚度、不同加劲肋数量及位置的钢模具应变分析

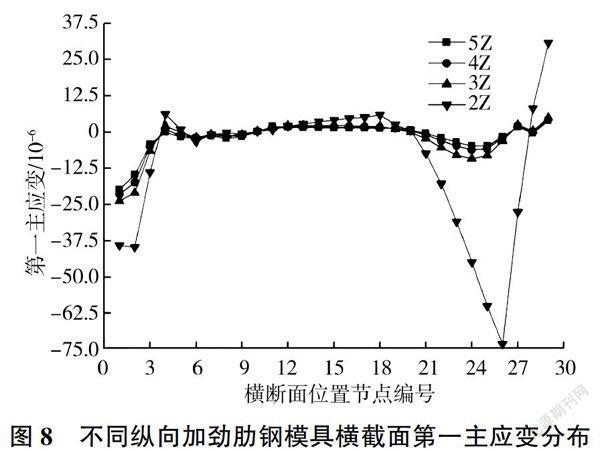
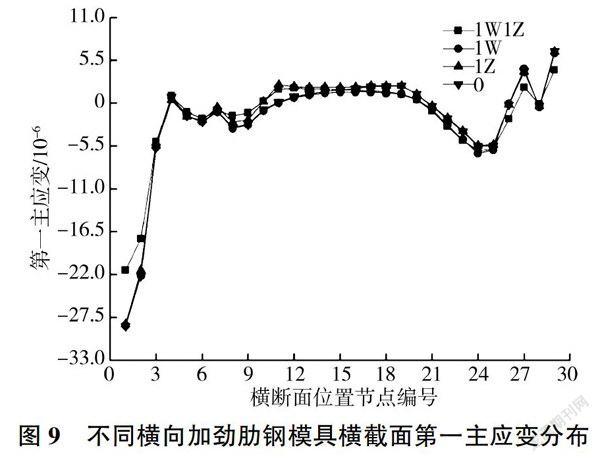
由于不同厚度钢模具的第一主应变分布随纵向加劲肋的数量和横向加劲肋数量及位置变化的趋势是一致的，因此本文只列出同一厚度（8mm）的不同纵向加劲肋、不同横向加劲肋及位置的钢模具的第一主应变分布图，见图8～图10。

由图8可知，当厚度和横向加劲肋及位置一定时（直线段和弧线段分别布置横向加劲肋），随着纵向加劲肋数量的增加，钢模具第一主应变逐渐减小，并且在直线连接段较大，弧线段次之，直线段最小。纵向加劲肋数量为2的钢模具直线连接段、直线段、弧线段的第一主应变分别为3.97×10-5、5.92×10-6和7.32×10-3，纵向加劲肋数量为3的钢模具直线连接段、直线段、弧线段的第一主应变分别为2.10×10-5、1.98×10-6和9.29×10-6，比纵向加劲肋为2的钢模具分别减少了47.10%、66.55%和87.31%。在纵向加劲肋的数量由3至5变化时，第一主应变逐渐减小，但是变化幅度较小。

由图9可知，横向加劲肋数量由0至1变化时，直线连接段、直线段、弧线段的第一主应变几乎一致，横向加劲肋布置在弧线段和布置在直线段相比，钢模具各部位的第一主应变绝对值变化不大，对钢模具的结构变形几乎没有影响。横向加劲肋的数量为1时，直线连接段、直线段、弧线段的第一主应变分别为2.83×10-5、2.13×10-6和5.40×10-6；横向加劲肋数量为2（1W1Z）时，钢模具模型的直线连接段、直线段、弧线段的第一主应变分别为2.15×10-5、1.23×10-6和3.53×10-6，比横向加劲肋为1的钢模具模型分别减小了24.03%、42.25%和34.63%，且在横向加劲肋的数量为2（1W1Z）时，钢模具的第一主应变分布较为均匀，这有利于预制混凝土衬砌板的脱模，提高预制混凝土衬砌板的平整度和制作效率。

由图10可知，当纵向加劲肋数量和横向加劲肋的数量及位置一定时，随着钢模具的厚度增加，其第一主应变逐渐减小，并且在直线连接段较大，弧线段次之，直线段最小。厚度为5mm的钢模具直线连接段、直线段、弧线段、弧线段端部的第一主应变分别为5.46×10-5、5.53×10-6、8.55×10-6和1.38×10-5；厚度为8mm的钢模具直线连接段、直线段、弧线段、弧线段端部的第一主应变分别为2.15×10-5、1.62×10-6、6.13×10-6和2.05×10-6；厚度为10mm的钢模具第一主应变与厚度为8mm的钢模具第一主应变相差很小；厚度为12mm的钢模具直线连接段和弧线段的第一主应变分别为1.63×10-5和4.56×10-6，比厚度为10mm的钢模具第一主应变分别减少了24.19%和25.61%，其他位置第一主应变相差很小。由此可知，当厚度分别为10、12mm时，厚度的增加对钢模具第一主应变的影响程度逐渐减小。

2.4 不同厚度和横、纵向加劲肋数量及位置对钢模具变形均方差的影响

为了较准确地评价厚度、纵向加劲肋数量和横向加劲肋数量及位置的变化对钢模具变形的影响，本研究采用钢模具横断面各节点变形均方差S作为评价指标，其值越大，表明钢模具的变形越大，对钢模具在施工过程中的影响越大。式中：S为均方差；ni为节点变形值；K（n）为节点平均变形值；n为节点数量。

计算结果见表3，其变形均方差与加劲助数量及位置的关系见图11。

由表3及图11可知，钢模具的变形均方差S随厚度的增大而减小，加劲肋数量为3ZIWIZ时，厚度分别为5，8、10、12mm的钢模具变形均方差分别为0.0202、0.0113、0.0101、0.0079mm；在横向加劲肋一定的情况下，随着纵向加劲肋数量的增加，钢模具变形均方差S逐渐减小；厚度为8mm、横向加劲肋数量为1w1Z时，纵向加劲肋2Z、3Z、4Z、5Z的钢模具变形均方差分别为0.0615、0.0113、0.0086、0.0070mm；在纵向加劲肋一定时，其变形均方差相差不大，在厚度为8mm、纵向加劲肋数量为3Z时，横向加劲肋为0、1W、1Z、1W1Z的钢模具变形均方差分别为0.0096、0.0094、0.0097、0.0086mm；在直线段和弧线段分别布置横向加劲肋时，均方差平均减小了10.09%。

3 结论

（1）钢模具的变形随纵向加劲肋的数量（2-5根）或厚度（5～12mm）的增加而減小，在钢模具中间位置的变形较大，两端的变形较小，等效应力随厚度及加劲肋数量的增加而减小，钢模具中间位置的等效应力较小，两端的等效应力较大。

（2）钢模具的第一主应变在两端最大，弧线段次之，直线段最小。纵向加劲肋的数量为3-5根、横向加劲肋的数量为1～2根和厚度为8～12mm时，钢模具第一主应变变化相对较均匀；纵向加劲肋数量为2根、横向加劲肋数量为0和厚度为5mm时，钢模具的第一主应变不均匀性的变化梯度很大，容易造成钢模具表面不均匀的凹凸现象。

（3）钢模具厚度为10～12mm时，变形的变化梯度较小，即对抵抗钢模具破坏效果不显著；厚度为5-10mm时，厚度的增加对钢模具的影响显著。钢模具纵向加劲肋数量为2-4根时，钢模具变形的变化梯度较大，即对抵抗钢模具的破坏效果显著；纵向加劲肋数量为4-5根时，纵向加劲肋的增加对钢模具的影响不显著；钢模具横向加劲肋数量为2（直线段和弧线段分别布置1根横向加劲肋）时，钢模具的变形和等效应力均较小。

参考文献：

[1]郭利霞.渠道冻胀力学模型及有限元分析[D].杨凌：西北农林科技大学，2007：68-70.

[2]王正中.梯形渠道混凝土衬砌冻胀破坏的力学模型研究[J].农业工程学报，2004（3）：24-29.

[3]王正中，李甲林，陈涛.弧底梯形渠道混凝土衬砌冻胀破坏的力学模型研究[J].农业工程学报，2008（1）：18-22.

[4]李学军，费良军，李改琴.大型U形混凝土衬砌渠道季节性冻融水热耦合模型研究[J].农业工程学报，2008（1）：13-17.

[5]郑源，汤骅，姜海波.梯形复合衬砌渠道冻胀破坏力学模型研究[J].人民黄河，2014，36（5）84-86.

[6]李翠玲，王红雨.两拼式U形渠道混凝土衬砌结构冻胀破坏力学模型[J].中国农村水利水电，2014（5）；86-89.

[7]闫长城，王正中，刘旭东，等.季节性冻土区玻璃钢防渗渠道抗冻胀性能初探[J].人民黄河，2011，33（3）：140-142.

[8]程传胜，田军仓，王斌，等.旱寒地区U形玻璃钢和混凝土渠道抗冻胀性能的研究[J].水资源与水工程学报，2016，26（6）：173-177.

[9]高靖，田军仓，王斌.装酉乙式U型混凝土渠道抗冻有限元模型及数值模拟研究[J].灌溉排水学报，2015，4（4）：38-42.

[10]李瑞军.盾构管片模具设计及性能分析[D].石家庄：石家庄铁道大学，2014：56-57.