机组水平动荷载对机墩振动反应的影响
高朦伟 方朝阳


摘要:水电站发电机组运行时将产生激振力,机墩作为发电机组主要支撑部位,其发生的振动现象较厂房结构其他部位明显。通过建立某水电站地下厂房三维有限元模型,采用谐响应法进行动力计算,研究实际工程中在不同机组水平动荷载施加方式下机墩各典型部位振动反应的分布规律。分析结果表明,机组水平动荷载的施加方式对机墩部位的振动影响很大,应根据机组动荷载的实际特性选取合适的施加方式才能充分考虑机组振动时产生的不利影响。
关键词:机组水平动荷载;施加方式;机墩;谐响应法;振动反应
中图分类号:TV731 文献标志码:A doi:10.3969/j.issn.1000-1379.2018.03.026
引起厂房结构振动的原因主要包括电磁力、机械力及水力等[1-2],这些力相互影响、错综复杂,随着水电站厂房尺寸和装机容量的增大,在这些力的作用下,厂房结构发生整体或局部振动的可能性加大[3-7]。机墩部位刚度相对较低,更容易受到机组运行时所产生的机组动荷载的影响,从而发生较为明显的振动现象。在实际工程中,发电机组制造厂家提供了水电站厂房结构动力计算所需要的机组动荷载参数,给出了单块基础板所承受的各向动荷载幅值。对于轴向和扭转动荷载可以等效为竖向和切向力,均匀施加在各基础板对应节点上;水平离心力的作用可以等效为各基础板对应节点上的径向力[8-9]。但实际运行过程中机组运行产生的离心力的方向是不断变化的,导致各基础板受力不均匀,并不能保证每块基础板上都能同时达到厂家提供的径向荷载数值,离心力也就不能简单地等效为均匀分布的径向力施加在全部受力基础板对应节点上。
1 计算模型
某水电站地下厂房主机间内安装2台机组,总装机容量为246mW,机组运行额定水头为177m,最大工作水头为210m,机组正常转速为250r/min,飞逸转速为456r/min。地下厂房实际开挖尺寸为84m×21m×49m(长×宽×高);机墩内径为5.3m,外径为10.1m;风罩内径为10.6m,外径为11.8m。笔者利用大型通用有限元计算软件ANSYS建立相应的三维有限元模型,运用动力有限元基本理论,计算并分析在不同机组水平动荷载施加方式下机墩结构的振动反应分布规律。
为使模拟机墩部位在机组振动荷载作用下的振动反应结果更为准确,选取2#机组段建立了厂房整体结构有限元计算模型。按照实际尺寸对主厂房结构进行模拟,采用三维实体单元solid45模拟混凝土结构,壳单元she1163模拟座环、蜗壳及尾水管钢衬,质量单元mass2l模拟主要机电设备及流道中的水,弹簧单元combine14模拟围岩的约束作用。边界条件:集水井底部和尾水管底板与围岩之间的接触按刚性连接处理,其余部位与围岩的接触采用弹性连接处理。计算模型采用笛卡儿直角坐标系:坐标系零点在机组安装高程处;X轴为水平向,面向下游指向左岸为正;Y轴为竖直向,向上为正;Z轴为顺水流向,指向下游为正。
采用C25混凝土,重度为25kN/m,,泊松比为0.167,动弹性模量为36.4GPa;钢的重度为78.5kN/m3,泊松比为0.3,动弹性模量为267.8 GPa;围岩单位抗力系数为55kPa/cm。谐响应计算中阻尼比取0.05。厂房三维整体计算模型节点总数为120239,單元总数为135021。
2 机组水平动荷载施加方式
当机组以恒定转速运行时,产生的水平离心力实际上大小不会变化但其方向会随偏心方向变化而变化,因此需要探讨一个适当的施加方式来充分考虑机组水平动荷载对机墩结构振动产生的不利影响。谐响应法是将荷载当成简谐荷载来计算,即认为荷载方向不会变化但其幅值会按照正弦规律变化。
根据厂家提供的机组振动荷载资料,选取机组正常运行工况下的机组动荷载作为计算荷载(见表1),为研究其中的一般规律,对不同计算方案施加的荷载是相同的。
同时,为研究激励频率对结构振动的影响,选取荷载振动频率范围为0~4.17Hz(正常转频),分为4个子步(即1.00、2.00、3.00、4.17Hz)进行计算。因本文主要研究机组水平径向力的作用方式对结构动力特性的影响,故将切向和竖向荷载平均施加在6块基础板对应的节点上。将径向荷载按照以下3种计算方案施加:①方案一,假设径向力作用均匀分布在6块基础板上,各基础板均承受径向力,方向指向外侧;②方案二,假设径向力作用分布不均匀,只有靠近上游侧4块基础板承受径向力,方向指向外侧;③方案三,假设各基础板径向力分布极不均匀,只有靠近上游侧2块基础板承受径向力,方向指向外侧。
马震岳等[10]结合国内外抗振标准,提出了水电站厂房振动控制标准,见表2,本文计算结果将以此作为评价标准。
3 厂房结构振动反应分析
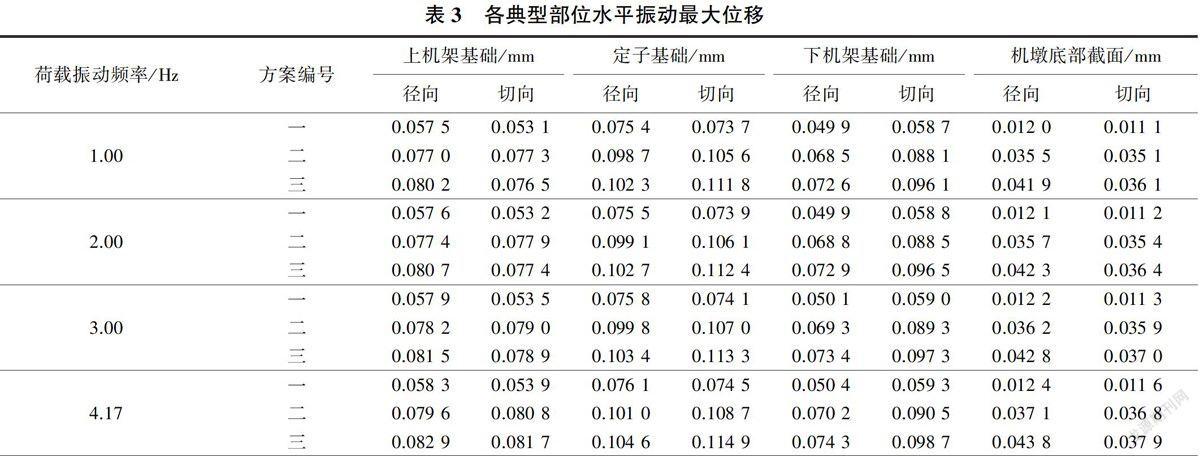
选取定子基础、上下机架基础及机墩底部截面等振动反应较明显的部位作为典型部位进行研究,由于各施加方案区别只在于考虑径向力作用方式的不同,因此只分析各典型部位的水平最大振动位移(见表3)。
从表3可以看出,各方案在4种振动频率下典型部位的水平振动位移均小于0.2mm,满足振动控制标准要求。随着振动频率的增大,各典型部位的最大振动位移逐渐增大,说明荷载振动频率对振动位移影响较大,处于4.17Hz转频下的机组动荷载更有可能引起机墩部位出现较大振动反应。同一振动频率下,基础板位置不同时径向动荷载施加方案的计算位移最大值排序为方案三>方案二>方案一。由于方案一将机组运行过程中产生的离心力分散为全部受力基础板上360°不同方向上的径向力,大大削弱了离心力对机墩部位产生的破坏影响,因此方案一的振动位移计算结果较方案二和方案三的结果小。方案二缺失下游两块基础板上的径向力,从而对机墩部位不平衡受力产生了贡献,因此在4种振动频率下,方案二各典型部位最大振动位移比方案一增大了30%以上,说明方案二的加载方式相比简单的将径向力施加到全部基础板上的做法更能充分考虑到离心力的不平衡性,对机墩部位的振动影响更大。方案三进一步考虑到径向力分布的不均匀性对厂房结构产生的不利影响,但其各典型部位各向最大振动位移在不同计算频率下相比方案二增大不多。考虑到方案三加载方式在实际运行中发生的可能性较小且相对于方案二对机墩部位振动位移的贡献提升不大,因此方案二的加载方式兼顾了实际运行过程中的概率和不利性,更为合理。各施加方案中,基础板位置处的最大振动位移要远大于机墩底部截面的,其中定子基础位置附近的最大振动位移较大。机墩底部截面的振动位移相对较小,说明基础板上直接承受机组动荷载的影响传递至机墩这种下部较大块体结构时会被直接削弱。
各典型部位水平振动的最大均方根速度及均方根加速度见表4、表5。
从表4可以看出,各典型部位水平振动的最大均方根速度与相应最大振动位移分布规律一致。不同振动频率下各典型部位的最大振动速度排序为方案三>方案二>方案一。因为振动速度与振动频率成正比关系,所以4.17Hz转频下的振动速度最大。由表5可知,不同机组水平动荷载施加方案下最大均方根加速度与最大均方根速度的排序关系一致,最大值出现的位置也相同。4.17Hz转频中最大均方根加速度相比其他振动频率对应计算值大得多,说明机组动荷载的计算频率对结构振动速度和加速度影响很大。当计算荷载振动频率取4.17Hz时,径向最大均方根加速度为0.0508m/s2,出现在定子基础位置,切向最大均方根加速度为0.0558m/s2,同样出现在定子基础位置,均远小于水电站主厂房振动控制标准建议值(1.0m/s2)。
4 结论
针对实际工程中机组制造厂家提供单块基础板上受力荷载的情况,重点计算并分析了不同机组水平动荷载施加方式对机墩部位振动反应的影响,得出以下结论:
(1)考虑机组运行产生的离心力的不同等效作用方式对机墩部位的动力响应有很大影响。在实际工程中,可以将厂家提供的基础板上切向和竖向动荷载等效施加在对应的全部受力基础板上,而径向动荷载应考虑各基础板上荷载不均匀分布的特性选取较为合理的施加方式。
(2)在机组动荷载作用下厂房结构动力有限元计算中,动荷载的计算频率对计算结果影响很大。各典型部位水平振动的最大均方根速度与最大动位移分布规律一致,振动速度与振动频率成正相关关系,最大均方根加速度与最大均方根速度之间也有类似关系。
参考文献:
[1]董毓新,李彦硕.水电站建筑物结构分析[M].大连:大连理工大学出版社,1995:157-158.
[2]马震岳,董毓新.水轮发电机组动力学[M].大连:大连理工大学出版社,2003:51-107.
[3]马震岳,宋志强,陈婧,等.小湾水电站地下厂房动力特性及抗震分析[J].水电能源科学,2007,25(6):72-74.
[4]陈婧,马震岳,戚海峰,等.宜兴抽水蓄能电站地下厂房结构振动响应分析[J].水电能源科学,2009,27(3):81-83.
[5]马震岳,沈成能,王溢波,等.红石水电站厂房的机组诱发振动及抗振加固研究[J].水力发电学报,2002,76(1):28-36.
[6]宋志强,马震岳,陈婧,等.龙头石水电站厂房振动分析[J].水利学报,2008,39(8):916-921.
[7]毛柳丹.大型水电站地下厂房振动特性反馈研究[D].天津:天津大学,2014:1-4.
[8]宋志強.水电站机组及厂房结构耦合振动特性研究[D].大连:大连理工大学,2009:60-62.
[9]孙万泉.水电站厂房结构振动分析及动态识别[D].大连:大连理工大学,2004:23-24.
[10]马震岳,张运良,陈蜻,等.水电站厂房和机组耦合动力学理论及应用[M].北京:中国水利水电出版社,2013:90-93.

