Developing individual tree-based models for estimating aboveground biomass of five key coniferous species in China

Weisheng Zeng•Liyong Fu•Ming Xu•Xuejun Wang•Zhenxiong Chen•Shunbin Yao

Abstract Estimating individual tree biomass is critical to forest carbon accounting and ecosystem service modeling.In this study,we developed one-(tree diameter only)and two-variable(tree diameter and height)biomass equations,biomass conversion factor(BCF)models,and an integrated simultaneous equation system(ISES)to estimate the aboveground biomass for five conifer species in China,i.e.,Cunninghamia lanceolata(Lamb.)Hook.,Pinus massoniana Lamb.,P.yunnanensis Faranch,P.tabulaeformis Carr.and P.elliottii Engelm.,based on the field measurement data of aboveground biomass and stem volumes from 1055 destructive sample trees across the country.We found that all three methods,including the one-and two-variable equations,could adequately estimate aboveground biomass with a mean prediction error less than 5%,except for Pinus yunnanensis which yielded an error of about 6%.The BCF method was slightly poorer than the biomass equation and the ISES methods.The average coefficients of determination(R2)were 0.944,0.938 and 0.943 and the mean prediction errors were 4.26,4.49 and 4.29%for the biomass equation method,the BCF method and the ISES method,respectively.The ISES method was the best approach for estimating aboveground biomass,which not only had high accuracy but also could estimate stocking volumes simultaneously that was compatible with aboveground biomass.In addition,we found that it is possible to develop a species-invariant one-variable allometric model for estimating aboveground biomass of all the five coniferous species.The model had an exponent parameter of 7/3 and the intercept parameter a0could be estimated indirectly from stem basic density(a0=0.294 ρ).

Keywords Biomass models·Allometric equations·Biomass conversion factor·Error-in-variable simultaneous equations

Introduction

The estimation of carbon sequestration capacity of forest ecosystems has increasingly attracted wide attention because forests play an important role in global carbon cycles(Fang et al.2001;IPCC 2003;Woodbury et al.2007).Forest biomass and its dynamics determine forest carbon storage that is the product of biomass and carbon content factor(CCF).The CCF has relatively small variation among different species and many studies have used an average value of 0.5 for various species(Ma and Xie 1996;Fang 2000;Liu et al.2000;Fang et al.2001).The Intergovernmental Panel on Climate Change(IPCC)also recommended 0.5 as the default value for carbon content in‘‘Good practice guidance for land use,land-use change and forestry’’(IPCC 2003).Therefore,modeling forest biomass is critical to forest carbon accounting,trading,and management.

Direct measurements of forest biomass are destructive and labor consuming.Thus,forest biomass has been often estimated using indirect methods such as biomass equations and the biomass factor conversion method(Fang et al.2001;IPCC 2003;Somogyi et al.2007).Biomass equations have been most commonly used over wide regions and have a long history.Thousands of biomass equations have been developed for tropical,subtropical,temperate,and boreal species and forests globally(Ter-Mikaelian and Korzukhin 1997;Jenkins et al.2003;Zianis et al.2005;Návar 2009;Henry et al.2013).Most of these were allometric equations which could be explained by the metabolic theory of West,Brown and Enquist for the origin of allometric scaling laws(West et al.1997,1999).The biomass factor conversion method relies on a biomass expansion or conversion factor which can be used alone or in combination with other variables to estimate biomass from stem volumes.The biomass expansion factor(BEF)has been widely used for this purpose(Brown and Lugo 1984;Fang et al.2001;IPCC 2003).Large-scale forest biomass estimations usually require data from systematic forest inventories that provide a comprehensive coverage of forest types in various regions and their site and growth conditions(Somogyi et al.2007).In view of the importance of carbon stock assessment in forest ecosystems,the availability of biomass equations has long been a limitation.The first worldwide web platform Glob Allome Tree was developed to provide free access to one global database for existing volume,biomass and carbon allometric equations,but in the first version of the database,the equations were only compiled for Europe,North America and Africa(Henry et al.2013).Over the past decades,several hundred biomass equations have been published in China but most were based on local or small-scale surveys which could produce large biases when applied to the estimation of biomass at large-scales such as for the entire country(Feng et al.1999;State Forestry Administration 2014).

In recent years,many researchers have made considerable efforts to estimate forest biomass at large-scales and have established a number of biomass equations which can be used for widely distributed tree species(Jenkins 2003;Zianis 2005;Snorrason and Einarsson 2006;Muukkonen 2007;Návar 2009;Blujdea et al.2012;Fayolle et al.2013;Sileshi 2014;Bi et al.2015).But such equations are still rare in China,especially for major tree species(Zeng 2011).In order to improve the accuracy of forest carbon accounting,China launched a national program on modeling individual tree biomass in 2009.This program aims to develop new biomass equations for 34 tree species or species groups with a total of 10,500 trees to be sampled across the country(Zeng et al.2010).Some preliminary results of the program have been achieved (Zeng 2011,2014,2015a,b;Zeng and Tang 2011a,b,2012;Zeng et al.2011;Zou et al.2015),and this current research is based on a project under this national biomass program.It focuses on individual tree aboveground biomass modeling for five key coniferous species noted below.The objectives were to:(1)establish biomass equations for the five species and to add to the number of biomass equations for China on the web platform Glob Allome Tree;(2)compare different modeling approaches for estimating aboveground biomass at individual tree level;and(3)discuss the feasibility to develop a generic equation for all five species across their distribution ranges.

Materials and methods

Data

Data are from the National Biomass Modeling Program(NBMP)managed by the State Forestry Administration of China.Field destructive sampling has been completed for five species,namelyCunninghamia lanceolata(Lamb.)Hook.,Pinus massonianaLamb.,P.yunnanensisFaranch,P.tabulaeformisCarr.andP.elliottiiEngelm.,with a sample size of 301,301,150,149,and 154 trees,respectively.These sample trees were selected according to their diameter and height,and were evenly categorized into 10 diameter classes of 2,4,6,8,12,16,20,26,32 cm and≥38 cm forC.lanceolata,P.massonianaandP.yunnanensisand 2,4,6,8,12,16,20,24,28 cm and≥32 cm forP.tabulaeformisandP.elliottii.In each diameter class,the trees were classified into 3–5 height classes with 3–5 trees in each.Geographically,the trees were selected proportionally to their stock volume,and as a result,were located in 11 provinces forC.lanceolataandP.massoniana,three forP.yunnanensis,12 forP.tabulaeformis,and five forP.elliottii(Zeng 2011).P.elliottiiis the most important exotic coniferous species introduced to southern China and is grown in plantations.The other four species are native and grow in both natural and planted forests.C.lanceolataandP.massonianaare the most important coniferous species in southern China,andP.yunnanensisandP.tabulaeformisare the major coniferous species in the southwest and north of China,respectively.Plantations of these five species occupy more than a third of the coniferous plantations of the whole country.

For each sample tree,diameter at breast height was measured and after felling,the total trunk length(height from ground level to the trunk tip)and live crown length(from the base of first live branch to the top of the crown)were also measured.The trunks were divided into 11 sections at points corresponding to relative positions of 0,0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,and 0.9 of the height.Base diameters of all sections were measured both over-and under-bark,and the tree volume was computed using Smalian’s formula.The fresh weight of the stem was measured by three sections,upper(50–100%of tree height),middle(20–50%)and lower(0–20%).Six discs 3–5 cm thick and more than 500 g in weight(double for each section)were cut at points corresponding to relative positions of 70,35 and 10%of the tree height,and the fresh weights of the bark and debarked stem were measured.The fresh weight of stem bark was equal to the fresh weight of the stem multiplied by bark percent from discs.In addition,the fresh weight of the crown was measured at three layers(top,middle,and bottom),and one and three subsamples were selected for foliage and branches,respectively and weighed in the field.The subsamples were 300–500 g each.If the fresh weight of the whole branch or foliage was less than 300 g,then it was totally sampled.All discs and subsamples were oven-dried at 85°C in the laboratory until a constant weight was reached.According to the ratio of dry to fresh weight,each component biomass was computed and the aboveground biomass of the tree was obtained by summation.The sample collection procedure was implemented according to the technical regulation of ministerial standards(State Forestry Administration 2015).The details of the sample trees are listed in Table 1.The wood density for each tree was calculated as the ratio of oven-dry weight to the volume of fresh wood(trunk volume over bark)measured in situ in the field.

Model development

The commonly-used biomass equation and biomass conversion factor models(Parresol 1999;Zianis et al.2005;Zeng 2011)can be expressed as:

whereyis aboveground biomass(M)or biomass conversion factor(BCF),xkare variables which reflect the dimensions of the trees such as diameter at breast height(D)and total height(H), βkare parameters,and ε is the error term.TheBCFis defined as the ratio of aboveground biomass to stem volume(V),which is equivalent to biomass expansion factor(BEF)multiplied by wood density(d)in the volume-based estimation method recommended by IPCC(2003).

In this study,we used the weighted regression method to eliminate the heteroscedasticity commonly exhibited in biomass data by using specific weight functions derived from the residuals of biomass equations fitted through the ordinary least square(OLS)technique(Parresol 1999;Zeng and Tang 2011c).For biomass conversion factor modeling,we directly used the OLS regression technique to estimate the parameters because the BCF data mostly exhibited homoscedasticity.Individual tree biomass has been commonly estimated by a one-variable model based onD(diameter at breast height)or a two-variable model based on bothDandH(height).In addition,mixed models were used to analyze the significance of differences among the five species.

Tree biomass can also be estimated by the BCF models which may produce different results from the biomass equations.In order to make the results compatible,Bi et al.(2001)developed a system of additive equations for converting stem volume into four biomass components and total aboveground biomass.We applied another approach to integrate the biomass equations and the BCF models into a whole system by simultaneously fitting all the parameters together through an error-in-variable simultaneous equations approach(Tang et al.2001;Li and Tang 2006;Zeng and Tang 2012;Zeng 2015a,b).

Nonlinear mixed-effects models

Both mixed-effects modeling and dummy variable approaches can be used to establish species-specific biomass equations(Wang et al.2008;Zeng et al.2011;Fu et al.2012;Zeng 2015a).Earlier studies have shown that mixed-effects modeling is slightly better than the dummy variable approach in estimating biomass(Zeng 2015a).In addition,it has an advantage on testing the differences among various tree species.Therefore we applied the nonlinear mixed-effects modeling in this study because of the advances in nonlinear regression techniques(Li and Zhang 2010;Fu et al.2013a).The nonlinear mixed-effects one-and two-variable individual tree biomass equations,including species-level random effects are expressed as:

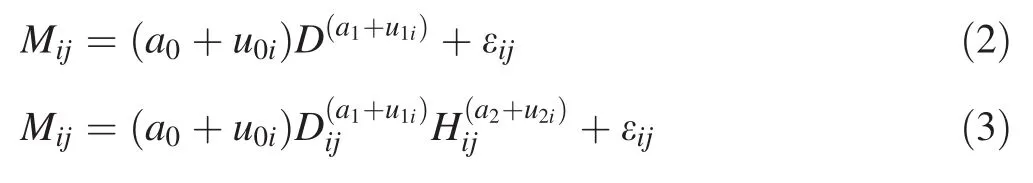
whereMij,DijandHijare the values of aboveground biomass(kg),diameter at breast height(cm)and total height(m)of thejth tree in theith species(j=1，...，ni,niis the total observations for theith species;i=1，...，5);a0，a1，a2are fixed-effects parameters;u0i,u1iandu2irepresent the random-effect parameters for theith species;εijis the estimation error for thejth tree in theith species.The values of ui= （u0i，u1i）Tor ui= （u0i，u1i，u2i）T(the superscriptTdenotes the matrix transpose operation)vary with the subscriptiand uiis assumed to be normally distributed with zero expectation and a variance–covariance matrix of ψ1.uiand εijare mutually independent.An F-statistic can be used to test if the parameter uiis significantly different from 0 at a confidence level of 0.05.The parameter uican be removed from the models if it does not significantly differ from 0.

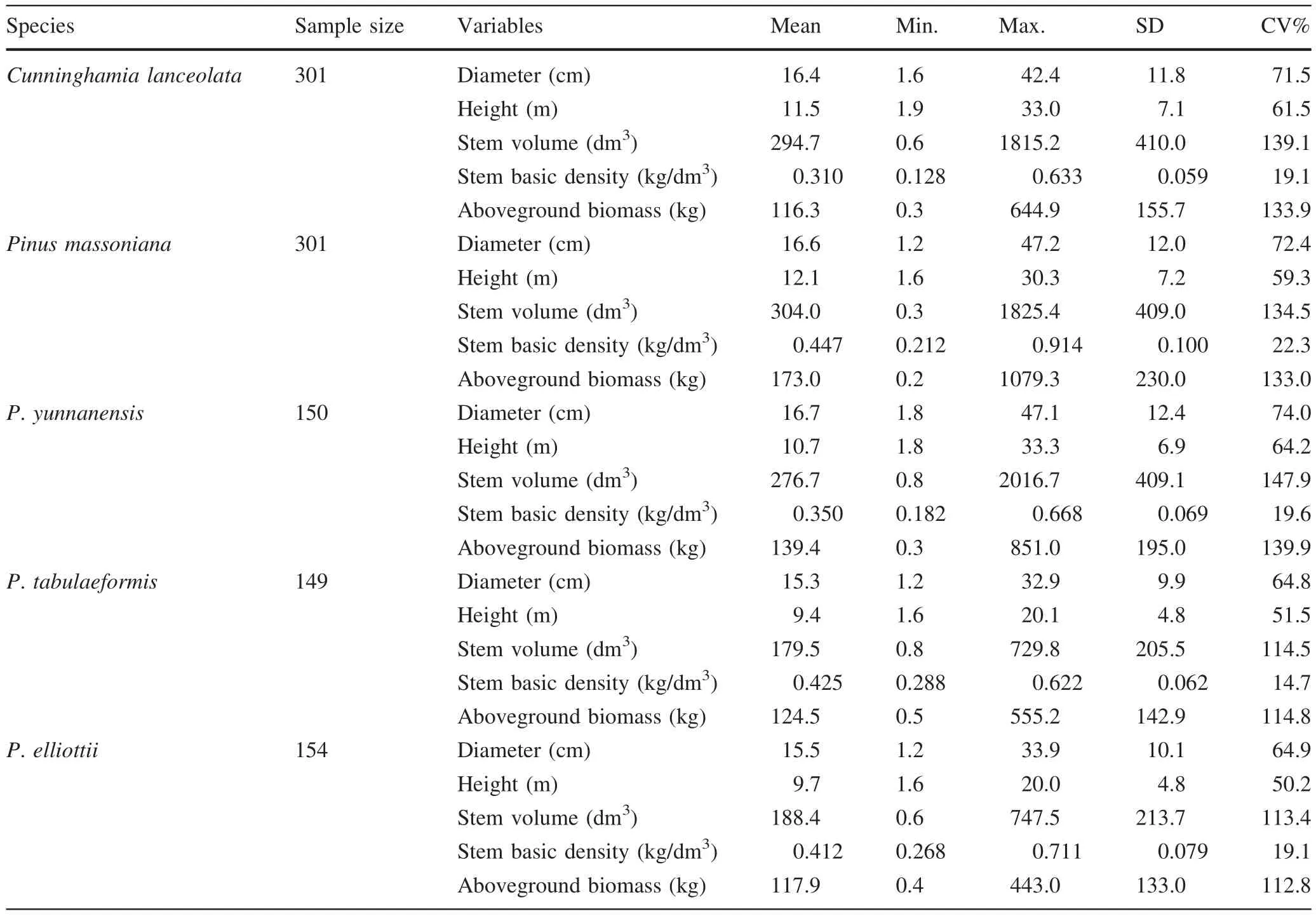
Table 1 Summary of the biomass data for the five conifer species

The tree stem volume equations are formulated similar to Eqs.2 and 3,and then the one-and two-variable nonlinear mixed-effects BCF models,which are equal to aboveground biomass equations divided by stem volume equations,can be expressed as:

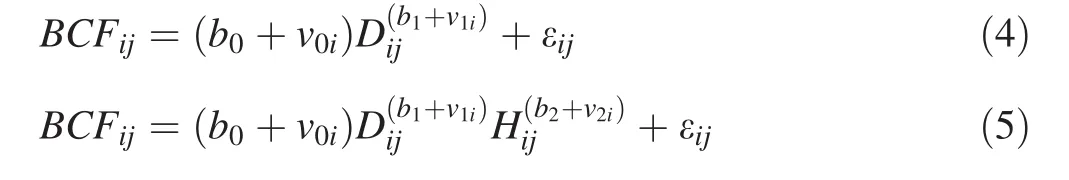
whereBCFijis the biomass conversion factor of thejth tree in theith species;b0，b1，b2are fixed-effects parameters;v0i,v1iandv2irepresent the random-effect parameters for theith species;vi= （v0i，v1i）Tor vi= （v0i，v1i，v2i）Tis assumed to be normally distributed with zero expectation and a variance–covariance matrix of ψ2;the other parameters and variables are as defined above.

We assumed that stem volume equations for the five species were not available or were biased,and it was necessary to develop tree stem volume equations when BCF models are applied for estimating aboveground biomass.The one-and two-variable tree stem volume equations are expressed as:

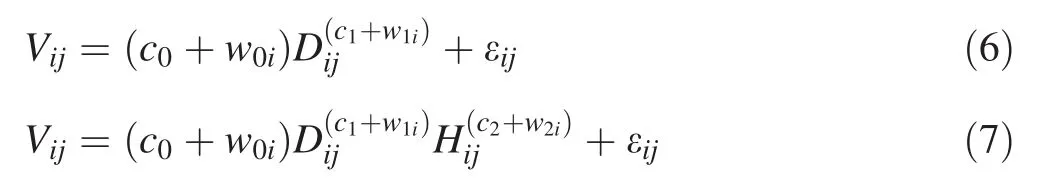
whereVijis the stem volume(dm3)of thejth tree in theith species;c0，c1，c2are fixed-effects parameters;w0i,w1iandw2irepresent the random-effect parameters for theith species; wi= （w0i，w1i）Tor wi= （w0i，w1i，w2i）Tis assumed to be normally distributed with zero expectation and a variance–covariance matrix of ψ3;the other parameters and variables are as defined above.

Detailed theories such as parameter estimation,model diagnostics and statistical inferences of nonlinear mixed effects models can be found in Tang et al.(2015)and Longford(2001).

Integrated simultaneous equations

The above models(Eqs.2–7)do not account for the correlations among the dependent variables.In fact,the aboveground biomass,biomass conversion factor and stem volume are all correlated to each other,and the aboveground biomass exactly equals stem volume multiplied by the biomass conversion factor.Therefore,the above one-or two-variable aboveground biomass equations,biomass conversion factor models and stem volume equations can be integrated as a set of simultaneous equations by setting some constraints for the parameters or model structure(Zeng 2015b).Solving these equations and models simultaneously will not only take advantage of the high correlations among diameter,height,volume,and biomass,but also will ensure the compatibility among aboveground biomass equation,biomass conversion model and stem volume equation.

Various methods have attempted to estimate the parameters of the simultaneous equations.Borders(1989)proposed the two-or three-stage least square regression method for estimating the parameters of a forest growth and yield modeling system.Parresol(1999)used the seemingly unrelated regression(SUR)for solving the additivity of simultaneous biomass equations.Tang et al.(2001)further developed the error-in-variable(EIV)modeling approach to estimate the parameters of simultaneous equations,which has been widely used in recent years(Li and Tang 2006;Zeng and Tang 2010,2012;Zeng 2015b,Zou et al.2015).Fu et al.(2016)compared the commonly used SUR with EIV for developing a system of nonlinear additive biomass equations,and concluded that the EIV approach had greater potential than SUR to develop equation systems.Thus,in this study we used EIV to estimate the parameters of a set of integrated simultaneous equations composed of an aboveground biomass equation,a stem volume equation,and a BCF model(Eqs.8 and 9).Considering that simultaneous equations with mixed models have not been solved as yet and the difference between the mixed model and the dummy model is very little with a large sample size(Wang et al.2008;Zeng 2015a), we introduced dummy variables to the simultaneous equations to reflect the differences in the parameters among tree species.

We created the following dummy variables:(a)Z1=1 denotesC.lanceolataand 0 the rest of cases;(b)Z2=1 denotesP.massonianaand 0 the rest of cases;(c)Z3=1 denotesP.yunnanensisand 0 the rest of cases,and(d)Z4=1 denotesP.tabulaeformisand 0 the rest of cases.P.elliottiiis represented byZ1=Z2=Z3=Z4=0.Thus,the one-and two-variable integrated error-in-variable simultaneous equations would take the following forms:

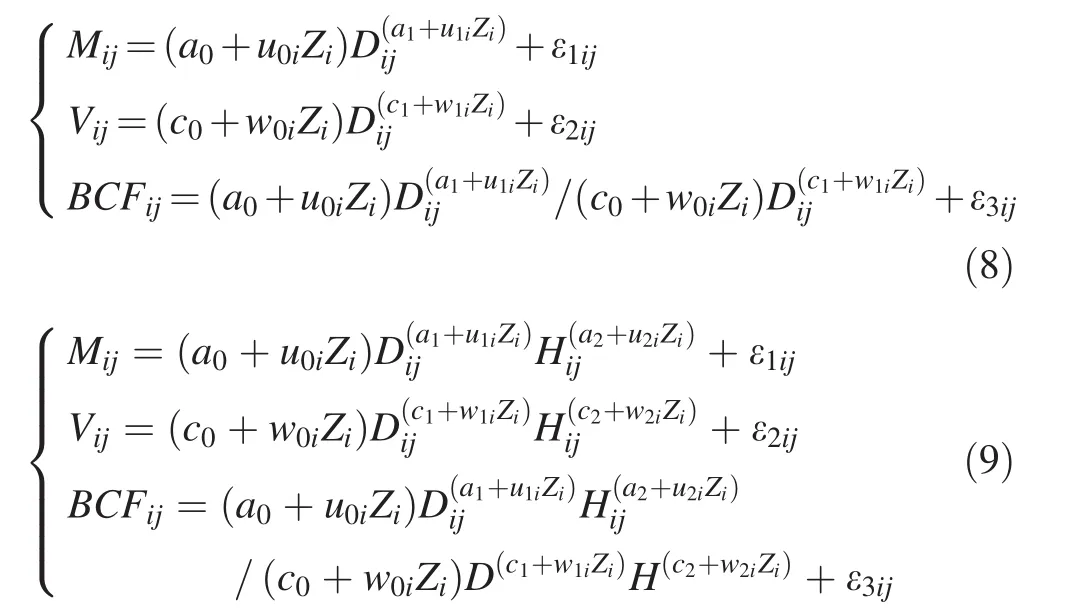
whereMij,VijandBCFijare aboveground biomass,stem volume and biomass conversion factor of thejth tree in theith species,respectively,which are treated as error-invariables;DandHare diameter at breast height and total height of thejth tree in theith species,respectively,which are treated as error-free variables;eij= （ε1ij，ε2ij，ε3ij）Tare independent and normally distributed three-dimensional vectors with zero mean and respective variance–covariance matrix Σ with 3 × 3 dimension;different from the definitions in the Eqs.(2)–(7),u0i，u1i，u2i，v0i，v1i，v2i，w0i，w1i，w2iare species-specific fixed-effects parameters;and the other parameters and variables are as defined above.

Model evaluation

Based on the measurements of diameter,height,aboveground biomass,stem volume and biomass conversion factor of 1055 sample trees for five coniferous species across their whole distribution ranges,we fitted Eqs.(2)–(7)using the ‘‘nonlinear mixed model’’approach,and Eqs.(8)and(9)using the ‘‘error-in-variable simultaneous equations’’approach through the ForStat software(Tang et al.2001;Fu et al.2013b).To clearly show the fitting results,we defined three approaches as:the biomass equation(BE)method,the biomass conversion factor(BCF)method,and the integrated simultaneous equations system(ISES)method.

Many statistical indices can be used to evaluate individual tree biomass models(Parresol 1999).Zeng and Tang(2011a)conducted a synthetic analysis on the evaluation of individual tree biomass models and provided six important ones,namely,the coefficient of determination(R2),standard error of estimate(SEE),mean prediction error(MPE),total relative error(TRE),average systematic error(ASE)and mean percent standard error(MPSE).In this study,we used the same six statistical indices to assess the performance of various models as presented earlier.

whereytand^ytare the observed and predicted values,respectively,for thet-th observation,¯yis mean value of samples,nis the number of samples,pis the number of parameters,andtαis thet-value at confidence level α withn-pdegrees of freedom.

Results

Parameter estimates of the aboveground biomass,biomass conversion factor models and stem volume equations are presented in Table 2,and the statistical indices of the aboveground biomass estimates are in Table 3.

The results in Table 2 show that the aboveground biomass equations from the BE method and the biomass conversion factor models and stem volume equations from the BCF method were independent of each other.This means that the three sets of models were not compatible.The statistical indices of the aboveground biomass estimates in Table 3 show that the BE method was better than the BCF method,and that the ISES method was very close to the BE method.For example,the meanR2for the five species from the three methods are 0.944,0.938 and 0.943 respectively;the difference between the BE and the BCF methods is 0.006,but between the BE and the ISES methods only 0.001.The mean MPEs from the three methods are 4.26,4.49 and 4.29%respectively,the difference between the BE and the BCF methods is 5.4%,but between the BE and the ISES methods is only 0.7%.Obviously,the ISES method is the best selection in estimating aboveground biomass because this not only has high accuracy but can estimate stem volume simultaneously and compatibly with biomass.Our results show that the differences of the aboveground biomass of the five coniferous species were mainly reflected in the random or specific parameteru0in Eqs.2 and 3.This directly determined the average amount of aboveground biomass of a tree for different species with the same diameter or/and height.The smalleru0value meant that the species had the smaller biomass with the same size(DandH)of a tree.According to the parameter estimates from the ISES method in Table 2,we found that for the one-variable model,C.lanceolatahad the lowest aboveground biomass while the biomass forP.yunnanensis,P.elliottii,P.tabulaeformis,andP.massonianawas 9.1,29.6,40.7 and 46.5%respectively,greater than that ofC.lanceolatawith the same diameter(Fig.1).The two-variable model gave a similar result with a slight difference in the order of the five species.C.lanceolatastill had the lowest aboveground biomass whileP.yunnanensis,P.elliottii,P.massoniana,andP.tabulaeformishad biomass of 13.5,37.0,44.2 and 49.6%respectively,greater thanC.lanceolata.For the same tree size,in the one-variable model,P.massonianahad the largest aboveground biomass whileP.tabulaeformishad the largest biomass in the two-variable model.

Table 2 shows that the biomass conversion factor(BCF)decreased nonlinearly with increasing diameter for the onevariable models where the smaller trees had greater BCF values.In addition,the decreasing trend was variable among the five species,with the fastest decreasing trend forC.lanceolataand the least forP.elliottii(Fig.2).Obviously,the decreasing trend among the five species was well-associated with the negative exponent parameterb1,i.e.,greater absolute valueb1corresponding to a steeper decreasing trend.As BCF has often been used as a constant in volume-based biomass estimations,it is necessary to highlight that the volume to biomass conversion naturally follows a nonlinear relationship as illustrated by the results here.These results also provide an interesting comparison to that shown in Figure 4 of Bi et al.(2001)for two Australian tree species.For the two-variable models,BCF increased with diameter and decreased with height.That is,given the same diameter,the shorter trees had greater BCF values,and for the same height,the taller trees had greater BCF values.

The results show that all the aboveground biomass equations demonstrate good performance with the lowest coefficient of determination(R2)greater than 0.92,and the mean prediction error(MPE)less than 5%,except forP.yunnanensiswhich had a MPE of about 6%(Table 3).As expected,all the absolute values of TRE and ASE were less than MPE and less than 5%for the ISES method but failed to meet the needs for the BE and BCF methods.From the comparison between the one-and two-variable models,we found that the two-variable model was slightly better except forP.tabulaeformis.

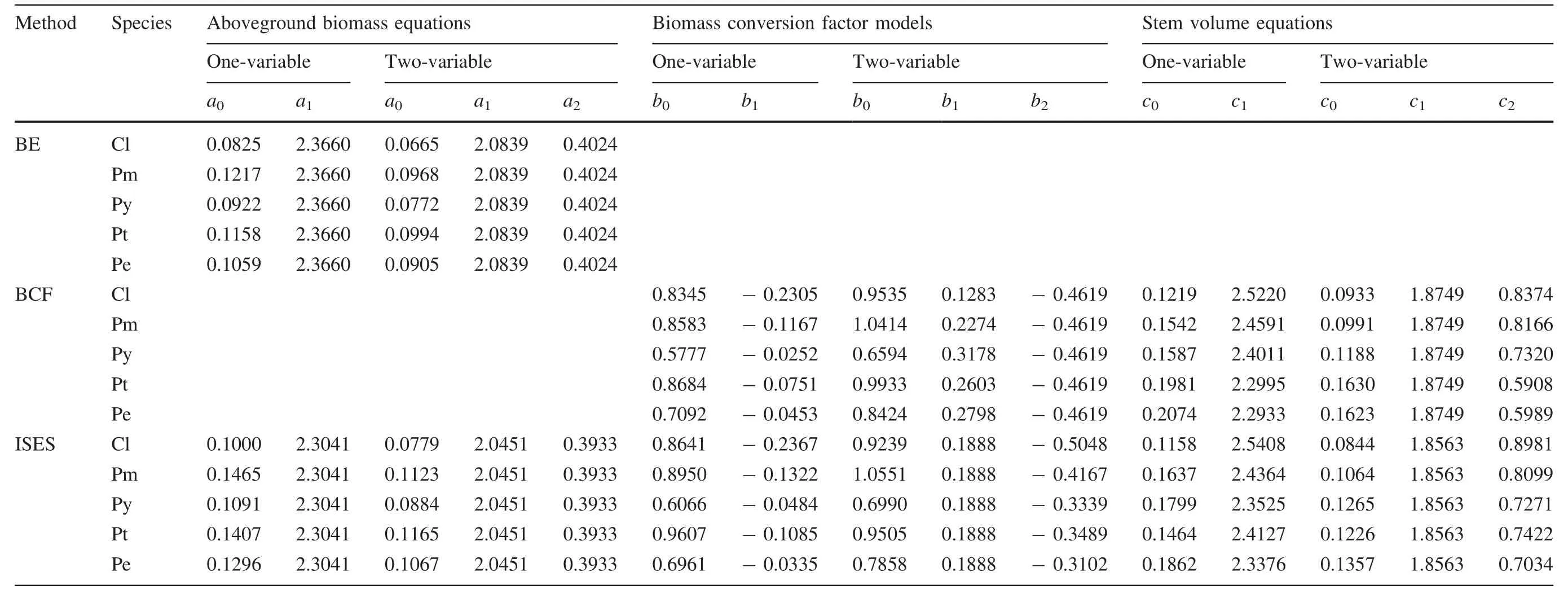
Table 2 Parameter estimates of the aboveground biomass,biomass conversion factor models and stem volume equations for the five conifer species from three methods(n=1055)

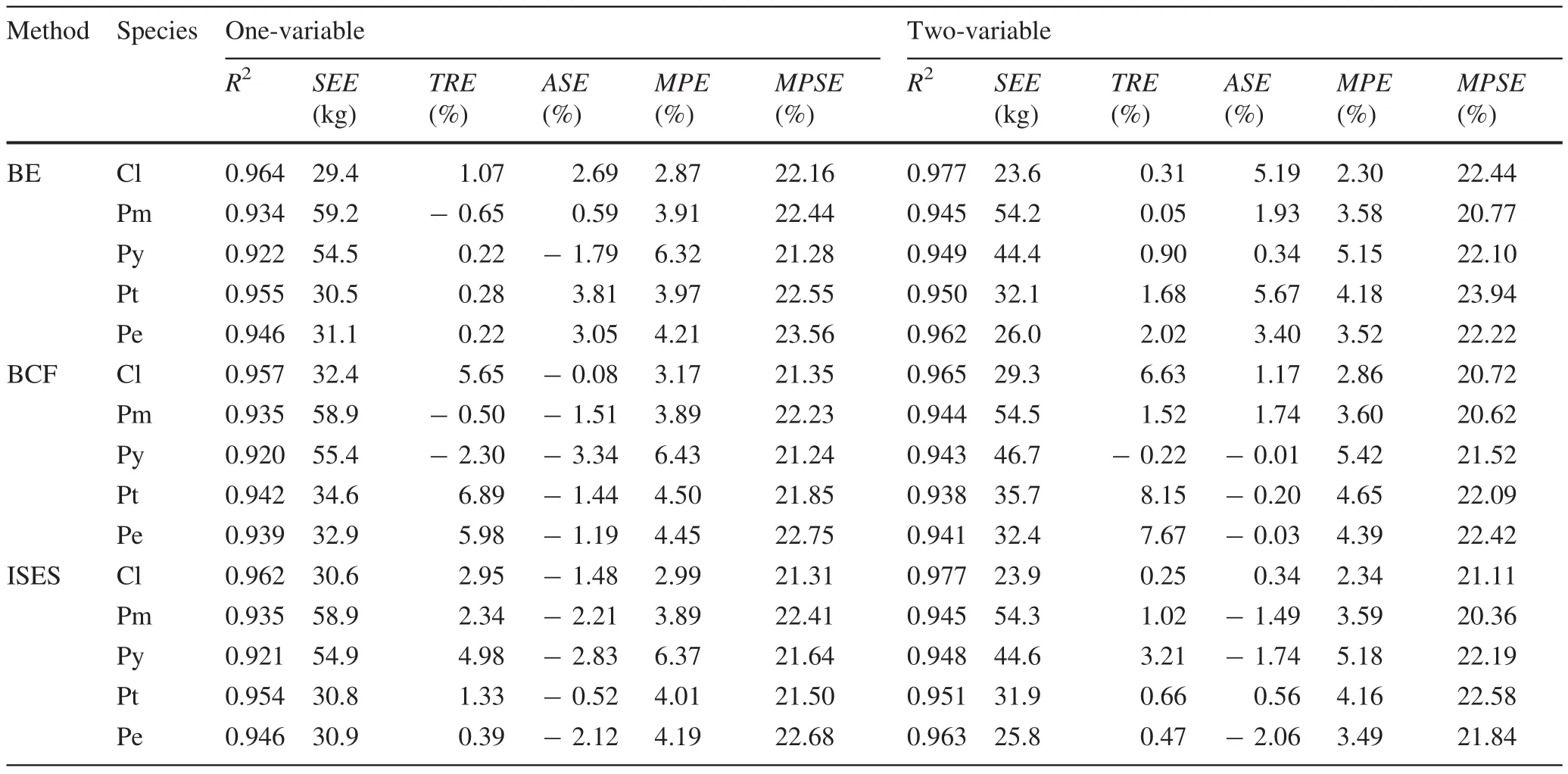
Table 3 Statistical indices of the aboveground biomass estimates for the five coniferous species through three methods

Fig.1 Relationships between aboveground biomass(M)and tree diameter(D).(Cl-Cunninghamia.lanceolata,Pm-Pinus massoniana,Py-P.yunnanensis,Pt-P.tabulaeformis,Pe-P.elliottii)

Discussion

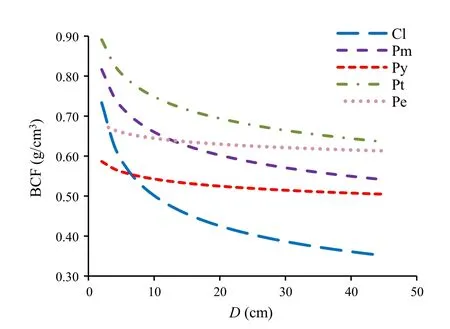
Fig.2 Relationships between the biomass conversion factor(BCF)and tree diameter(D).(Cl-Cunninghamia.lanceolata,Pm-Pinus massoniana,Py-P.yunnanensis,Pt-P.tabulaeformis,Pe-P.elliottii)

The one-variable(Donly)biomass equation was the most widely used model in estimating individual tree biomass(Jenkins et al.2003;Muukkonen 2007).The power function of the one-variable equation was based on the WBE theory for the origin of allometric scaling laws(West et al.1997,1999).Our results show that the two-variable(DandH)model was slightly better than the one-variable model,which was consistent with previous findings(Ma 1989;Feng et al.1999;Zeng and Tang 2012;Bi et al.2015;Zeng 2015b).The advantage of incorporating tree height in the predictor is that an adequate and more stable accuracy can be maintained when the equations are applied beyond the sampling sites,across wide environmental gradients and

over stands with different disturbance histories or at different stages of development(Bi et al.2015).However,considering the difficulty and errors involved in measuring tree heights in the field,we would like to recommend the one-variable model to estimate individual tree biomass when high quality height data are not available.Most of the challenges in developing and applying these empirical models come from the variation of the parameters among different species and in different regions.Searching the literature we found that biomass equations developed by different researchers for the same species and same region could produce a difference of＞50%(Ma 1989;Chen and Zhu 1989;Jenkins et al.2003;Muukkonen 2007),which drastically compromises the credibility of forest carbon accounting.However,in the current study,we found that the exponents in biomass Eqs.2 and 3 were not significantly different among the five species,suggesting a general biomass model might be possible for all or a group of species.It is worth special attention that based on branching networks and biomechanics of trees or vascular plants.West et al.(1997,1999)presented a general allometric model and derived such a formula,D∝M3/8,from complicated derivations based on several assumptions.Applying the formula to aboveground biomass estimations,it meant the power parameterb=8/3(≈2.67)in the allometricmodelM=aDb.However,an empirical assessment of tree branching networks and implications for plant allometric scaling models challenges the assumption of an optimized,symmetrically branching tree because the estimated scaling exponent significantly differs from theoretical predictions(Bentley et al.2013).The exponent value in the current study is 2.30 which is very close to the ratio of 7/3,confirming the results of our earlier study(Zeng and Tang 2012),and challenges the WBE theory(1997,1999).To further explore the possibility of developing a general allometric biomass model,we first substituted the parametera1in the one-variable model with 7/3(≈2.33).Then,we re- fitted the mixed model and estimated the parametera0.We found that thea0values forC.lanceolata,P.massoniana,P.yunnanensis,P.tabulaeformisandP.elliottiiwere 0.091,0.134,0.102,0.127 and 0.116,respectively.Furthermore,we found thatthe parametera0was highly correlated with the stem basic density of these species through a simple linear relationship:

where ρ is the basic density of stem(kg/dm3;the mean values for the five species are listed in Table 1).Because the intercept was not statistically different from 0,then we forced the regression line to pass the origin.The scalar value of 0.294 in Eq.16 is very close to the value of 0.3 as in our earlier study(Zeng and Tang 2012).Our results in Table 2 suggest that the differences of the biomass equations among different species may mainly be reflected in the parametera0,rather than the exponent,which can be estimated by the wood density of different species.Wood density data are widely available for various tree species in many countries and many regions(IPCC 2003),which may provide a feasible way to accurately estimate biomass of various species.In addition,we compared the performance of Eq.16(with a fixed exponent of 7/3)with the nonlinear mixed model(Eq.2)and found that the relative differences were 0.29,-1.78,1.27,-1.84 and 4.13%respectively,for the five species.Errors of such sizes are acceptable in biomass estimation.

This general allometric aboveground model is particularly useful when a reliable biomass equation is not available,especially for rare or endangered species where destructive sampling is impossible.For example,P.koraiensisSiebold&Zucc.is rare in northeastern China,and it is not feasible to collect biomass data by destructive sampling.However,we can collect a few samples for measuring the basic wood density and derive a biomass equation from Eq.(16).Assuming the stem basic density of

P.koraiensisis 0.362,then the corresponding biomass equation is:

As for species with relatively fewer numbers and without a separate biomass model,if necessary we can also use this method to get an approximate aboveground biomass equation.Of course,Eq.(16)is based only on the data of five species and further studies would be valuable to test this method for more species and in different regions.

Biomass equations have been widely used to estimate forest productivity and carbon sequestration.End-users may choose different equations such as the one-or two variable biomass equations or the biomass conversion factor equations,and thus may come up with quite different results even for the same portion of forest.Therefore,it is important to make the results compatible among different equations and methods.The integrated simultaneous equation system(ISES)method has been successfully used for this purpose(Zeng and Tang 2012;Zeng 2015b;Zou et al.2015).In the current study,we found that the accuracy of aboveground biomass estimated by the ISES method was not much different from that of the independently fitted biomass equations but it was apparently better than that of the BCF models.

Based on the results of this study,we recommend the following general guidelines for selecting methods and models:(1)if the existing stem volume table(or equation)was significantly biased(beyond an acceptable error),a new model needs to be developed.With a reliable model,the aboveground biomass equation and the biomass conversion factor model are equivalent in estimating biomass,both of which guarantee the compatibility between biomass and stocking volume;(2)if a good stem volume table(or equation)is not available and the estimation of stocking volume is required,a biomass conversion factor model is recommended to ensure the harmonization between biomass and volume;and(3)if an estimation of stand volume is not required,biomass equations can be used directly to estimate biomass irrespective of volume.

Furthermore,it should be noted that biomass equations and biomass factors usually involve two levels:the tree level and the stand level(Somogyi et al.2007).The biomass of trees includes both above and below ground biomass,and the biomass of a stand includes tree biomass and the biomass of the under story vegetation.The biomass equations and BCF models developed in this study are tree level models and only involve the aboveground biomass.The establishment of below ground biomass equations will be the next effort.

Conclusions

In this study,based on measurements of diameter,height,and stem volume from 1055 sample trees of five coniferous species,we developed one-and two-variable aboveground biomass equations,biomass conversion factor models,and a compatible simultaneous equation system to estimate the aboveground biomass.The equations and conversion factor models provide the basis for estimating the aboveground biomass for the five species and would fill in missing data for China on the web platform Glob Allome Tree.These equations and models have the potential to support the implementation of policies and mechanisms designed to mitigate climate change,such as Clean Development Mechanism(CDM)and Reducing greenhouse gas Emissions from Deforestation and forest Degradation in developing countries(REDD+),and to calculate costs and benefits associated with forest carbon projects.From this study,we conclude that:(1)the aboveground biomass could be estimated with a mean prediction error less than 5%except forPinus yunnanensiswhich had an error of about 6%;(2)the integrated simultaneous equation system(ISES)was effective to make the estimations of aboveground biomass and stocking volume compatible,and had similar accuracies as the independently- fitted biomass equations;(3)the biomass conversion factor(BCF)method was slightly poorer than the biomass equation and the ISES methods;and(4)a general one-variable(tree diameter only)model can be used to estimate the aboveground biomass for the five conifer species with a coefficient of determination greater than 0.92,where the five species had the same exponent value of 7/3 and the intercepta0could be accurately estimated by the basic density of wood.

AcknowledgementsWe acknowledge the National Biomass Modeling Program in Continuous Forest Inventory(NBMP-CFI)which was funded by the State Forestry Administration of China,for providing biomass measured data of 1055 sample trees ofC.lanceolata,P.massoniana,P.yunnanensis,P.tabulaeformisandP.elliottii;and thank the reviewers and editors for their valuable comments.

Compliance with ethical standards

Conflict of interestsThe authors declare that they have no conflict of interest.