基于粒子群优化的BP神经网络图像复原算法研究
王文中, 张树生, 余隋怀
(1.西北工业大学 陕西省工业设计工程实验室, 陕西 西安 710072; 2.陕西科技大学, 陕西 西安 710021)
图像退化和图像复原互为因果关系,由于各种外部和内部因素而导致图像质量的降低,我们称之为图像退化,其为因;而改善图像质量的数字图像处理技术,我们称之为图像复原(image restoration),其为果。图像复原通常是指应用计算机技术和数学理论,研究如何建立数学算法模型,把退化了的图像还原成原始图像,简而言之,图像复原过程就是退化的一个逆过程。图像复原对于图像分析、模式识别、特征元素提取等图像的进一步研究意义重大,已广泛用于科学研究、工程实践和日常生活中。
1 图像退化与复原模型
图像的老化,可以视为以下这样的一个退化过程:退化函数的影响(致使图片模糊,褪色等),叠加可加性噪声的影响[1]。本文研究的图像退化复原模型如图1所示。

图1 图像退化复原模型
原始图像f(x)经过一个算子或系统H作用后,和加性噪声η(x)相叠加,形成退化后的图像g(x),这一退化过程的表达式为:g(x,y)=H[f(x,y)]+η(x);H[*]在这里是指所有导致图像退化外在原因的函数集合。f′(x,y)是经过复原函数矫正后获得的复原图像[2]。
2 粒子群算法和BP神经网络
2.1 粒子群算法
粒子群算法是通过模拟鸟群觅食行为而发展起来的一种随机搜索算法[3]。在此基础上形成的粒子群优化算法,是以一个群体中个体与个体之间相互协作和共享信息从而寻找最优解来作为基本思路的。设定搜索空间是D维的,由m个粒子组成的一个种群,粒子的速度和位置就可以通过PSO公式来更新[4]。
PSO公式:
Vi=ωVi+c1r1(pbesti-xi)+c2r2(gbesti-xi);
xi=xi+Vi
c1,c2是学习因子或者加速系数,一般为正数,通常等于2;r1,r2取值范围通常是[0,1]的随机数。
2.2 BP神经网络
BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络[5]。简单的神经网络由输入层 、隐含层和输出层组成,假设有a个训练样本,即有P个输入输出(Ip,Tp),p=1,2,…,a;输入向量Ip=(ip1,…,ipm)T,目标输出向量Tp=(tp1,…,tpn)T,最终输出向量Op=(op1,…,opn)T;如图2所示。

图2 3层神经网络拓扑图

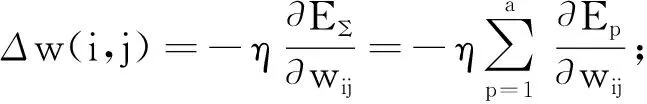
3 PSO-BP算法优化及调整方法
3.1 粒子群PSO算法优化
粒子群算法是一种全局优化的随机搜索仿生算法,隐含并行性,根据个体的适配信息进行搜索,不受函数约束条件的限制,如连续性、可导性等。但是对高维复杂问题,往往会遇到早熟收敛和收敛性能差的问题,无法保证收敛到最优点,这时一般的优化方法是引进收敛因子K是用来保证函数的收敛性。
Vi=K[Vi+φ1r1(pbesti-xi)+φ2r2(gbesti-xi)]
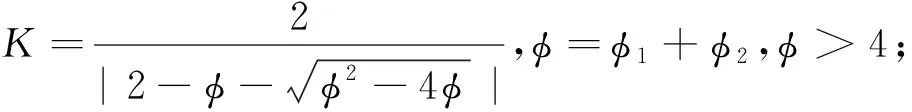
3.2 BP网络结构优化
BP算法简单、计算量小、并行性强,是目前最成熟的神经网络算法。但凡事皆有利弊,BP神经网络也不例外。总的来说,BP神经网络存在以下缺点:BP神经网络求解时很容易陷入局部极小值而得不到全局最优值。
针对易陷入局部极小值缺点,一般采用下列方法对BP算法进行改进:
1) 选取合适的初始权值以及修正权值,训练是从某一起始点沿误差函数的斜面逐渐达到误差最小值,初始值一旦确定,就注定了网络收敛的方向,所以选择合适的初始值就显得特别重要,只有通过多次随机训练最后选择效果最好的那个初始值;或借用退火思想调整E,允许E按照一定概率上升以增加跳出局部极小的可能;或弹性调整权值变化方向和大小,以改进误差函数。
2) 增加动量项:主要思想在于让第n次迭代时的权值的更新部分依赖于第n-1次的权值。即公式:Δwji(n)=η·δj·xji+αΔwji,动量因子 一般选取0.1~0.8。引入动量项一方面在一定程度上起到加大搜索步长,能加速算法收敛。另一方面可以降低网络对误差曲面局部调节的敏感性,从而有效地抑制了网络陷入局部最小值。
3)改变网络结构:网络结构优化的关键在于隐含层数与隐含节点数目,隐含节点过多,正面效应很容易提高精度,负面效应会造成网络结构庞大,性能下降。按照实验的数据统计,隐含层一般取20~40效果较好[7]。
4)采用自适应调节学习率:对学习率(或步长)的改进。修正量大小受学习率控制,学习率的大小对收敛速度和训练结构影响很大。步长小训练收敛稳定,但时间长、速度慢;反之,步长大可以加速收敛但容易导致震荡或发散;所以采用自适应调节学习率显得特别重要。
3.3 PSO-BP模型的自身优化
PSO-BP优化算法模型一方面用BP算法对各个训练样本的误差进行反传,并以辅助原始图像作为参考,共同修正BP算法的权值和阈值;另一方面又通过正向粒子群算法,寻找个体极值和全局的最优值,再进行解码并更新BP算法的权值和阈值。PSO-BP优化算法从寻找初始权值到对PSO算法进行优化,同时也对隐含层的网络结构进行优化。通过调整输入节点与隐含层节点的联接强度和隐含层节点与输出节点的联接强度以及阈值,使误差沿梯度方向下降,经过反复学习训练,最终得到最小误差相对应的网络权值和阈值。
为避开饱和区,提高训练速度和灵敏性,要求输入数据的值在0~1之间,所以先要对数据进行归一化处理,通常的做法是将要复原图像的初始灰度值统一除以255,这样输入数据就由[0,255]转换到了[0,1]。
4 基于粒子群优化的BP神经网络图像复原
4.1 PSO-BP优化算法步骤
一个群体规模为m的网络,构造优化PSO-BP算法模型,从而得到误差最小的最佳PSO-BP网络结构。采用3×3(像素)窗口在退化图像上滑动取样,其PSO-BP优化训练流程图,如图3所示。
该算法的学习过程包括“PSO信息的正向传播”和“BP误差的反向传播”2个过程。实际输出与期望输出的差即是误差,PSO-BP优化模型就是通过对各层神经元权阈值的不断修正,让误差函数沿梯度方向下降。这种PSO-BP优化算法使得总的误差一直减少,最终达到误差平方和小于目标误差ΣBP的目的[8]。

图3 PSO-BP优化训练流程图
4.2 PSO-BP优化算法MATLAB平台程序实现
我们在MATLAT平台中基于PSO-BP优化算法进行编程,语言采用MATLAB中兼容度最高的C++,部分代码截图如图4所示,经大量样本案例实验数据证实,可以达到该算法预期效果。
#include
#define LAYER 3 ∥3层神经网络
#define NUM 10 ∥每层的最多节点数
#defineA30.0
#defineB10.0 ∥A和B是S型函数的参数
#define ITERS 1 000 ∥最大训练次数
#define ETA-W 0.003 5 ∥权值调整率
#define ETA-B 0.001 ∥阀值调整率
#define ERROR 0.002 ∥单个样本允许的误差
#define ACCU 0.005 ∥每次迭代允许的误差
#define Type double
#define Vector std∷vector
struct Data
Vector
Vector
};
class BP{
public:
void GetData(const Vector);
void Train( );
Vector
private:
void InitNetWork( ); ∥初始化网络
void GetNums( ); ∥获取输入、输出和隐含层节点数
void ForwardTransfer(); ∥正向传播子过程
void ReverseTransfer(int); ∥逆向传播子过程
void CalcDelta(int); ∥计算w和b的调整量
void UpdateNetwork(); ∥更新权值和阀值
Type GetError(int); ∥计算单个样本的误差
Type GetAccu( ); ∥计算所有样本的精度
Type Sigmoid(const Type); ∥计算Sigmoid的值
图4 PSO-BP优化算法在MATLAB平台程序实现
4.3 PSO-BP优化算法总结
1)本文提出的PSO-BP优化算法在网络权值调整过程中,既考虑了由基本BP算法各个训练样本的误差反传进行的权值修正,又考虑训练完1遍后,通过跟踪个体网络历史最佳权值和群体网络历史最佳权值来更新权值,因而不同于传统的PSO-BP向前传播算法。
2)本算法模型采用优选网络结构有2大特点:①对不同的网络结构,都通过构造群体规模为m的不同初始权值和阈值的网络,并采用PSO-BP算法进行优化,从中优选得到误差最小的BP网络为最佳的网络结构,该方法也兼顾了初始权值和阈值的优选。②隐含层按照实验大数据最优结果为模板,收敛速度快,精度高,不受模型结构的影响。PSO-BP优化算法与BP算法和传统PSO-BP算法的训练结果相比,具有更小的训练误差和检验误差,在一定程度上提高了学习能力和泛化能力。
3)采用原始图像对PSO-BP优化算法进行直观校正,让复原图像尽量趋近于原始图像。然后再将经过反复修正的最优化模式用于其他失真图像复原上,可以更加精准的对图像进行复原。
5 仿真实验结果与分析
5.1 实 验
粒子群的规模本次实验设定为20,PSO-BP优化算法采用3×3(像素)的九宫格窗口来滑动提取退化图像,由此获得输入样本。把退化图像的某一点及其周围8个点的灰度值作为一个样本输入,把相应原始图像该点的灰度值作为目标输出。在BP算法反向训练权值时,采用梯度下降动量和自适应学习算法,其中变换函数采用的是Sigmoid型函数,均方误差目标设定为0.000 1。结果如图5所示:
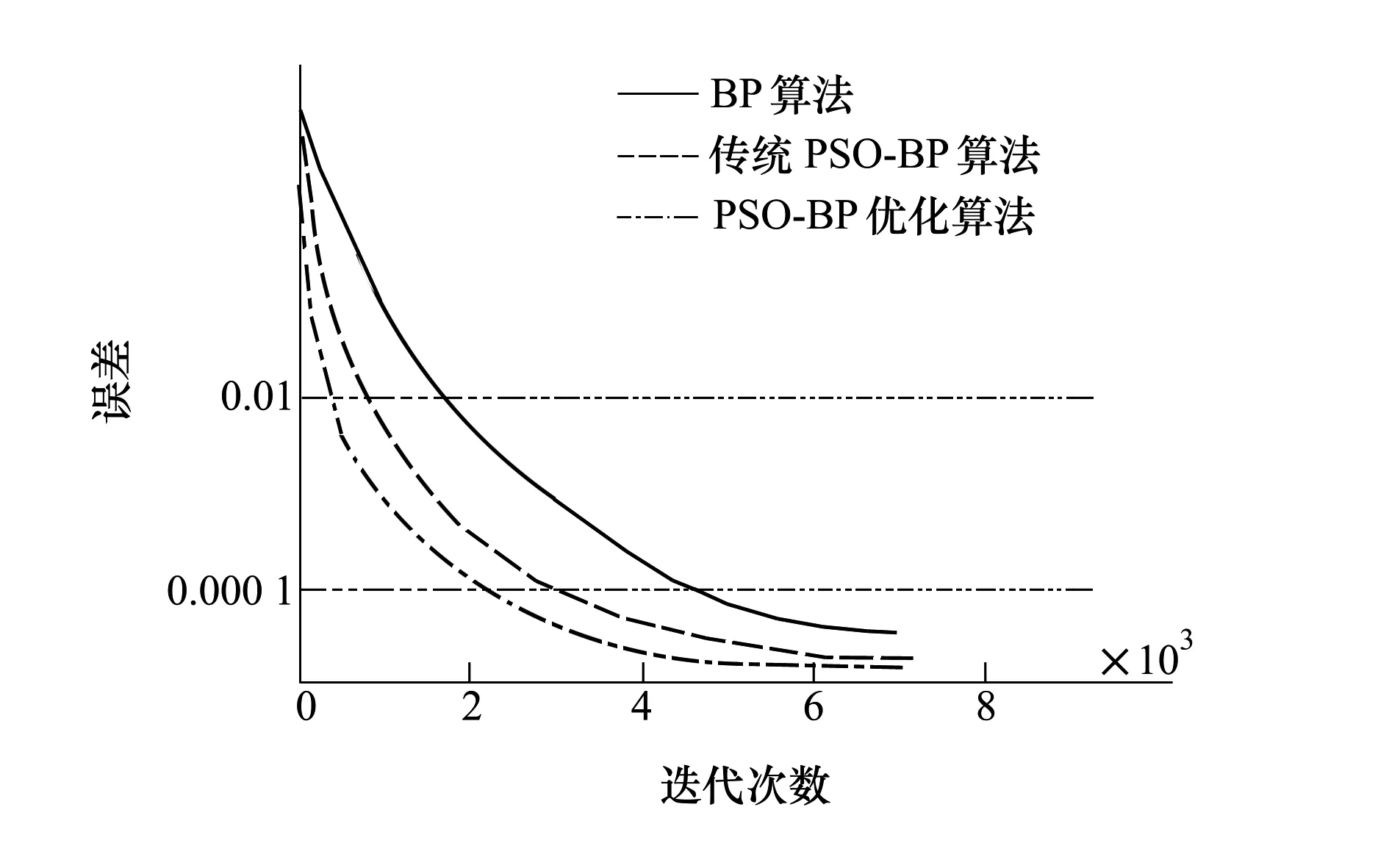
图5 3种算法的收敛曲线图比较
从图5不难看出,使用PSO-BP优化算法的收敛速度要比BP算法和传统PSO-BP算法快,复原效果也比其他2种都要好[9]。
表1为在给定3 000训练次数,不同BP算法分别在均方误差上的训练效果比较。

表1 不同BP算法训练结果比较
表1的训练结果表明,采用传统PSO-BP算法得到的均方误差比BP算法减少89.88%,而优化PSO-BP算法得到的均方误差比传统PSO-BP算法减少69.23%,从数据对比研究可以得出,PSO-BP优化算法的收敛速度明显优于其他2种算法。定量训练证明,优化PSO-BP算法是一种比较好的图像复原方法,特别是在图像边缘及纹理细节方面处理效果较好。
5.2 某款无人机图像复原对比
训练样本取某款无人机作为实验对象,采用3×3九宫格窗口从要复原图像上滑动提取样本,分别得到相关输入矩阵和输出矩阵,代入用3种算法进行训练,本次实验平台选择MATLAB。样本像素大小为128×128,复原效果如图6所示:
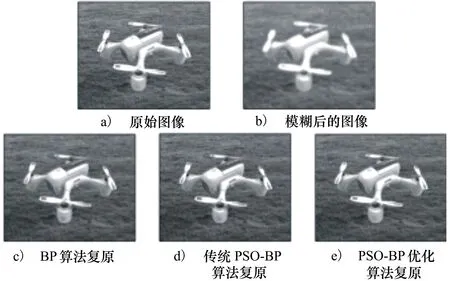
图6 某无人机图像复原效果对比
图6a)为原始图像,6b)为高斯模糊后的图像,6c)为用 BP算法复原的图像,6d)为用传统PSO-BP算法复原的图像,6e)为PSO-BP优化算法复原的图像。可以明显看出传统PSO-BP算法复原图6d)的效果要好于BP算法复原的图6c),而图6d)和6e)两图复原效果进行对比,显然是PSO-BP优化算法复原图像6e)的效果更好一些。
5.3 唐代仕女图像复原对比
训练样本取自某博物馆具有代表性的唐代仕女图像,由于时代久远、保存手段限制等原因,图像严重失真,采用3×3九宫格窗口从退化图像上滑动提取样本,代入用3种算法进行训练,实验平台选择MATLAB。样本像素选择大小为200×300,这个例子不同的是,按照上一例原始参考图调整的取样值来更新BP神经网络的权阈值,复原效果如图7所示:
图7a)为唐代仕女的失真图像,复原后的图像图6b)~d)复原效果对比是依次变好。可以看出:在引入上一例参考原始图像进行微调校正的优化复原模式,用在仕女失真图上,复原效果比其他模式更好也更精准[10]。
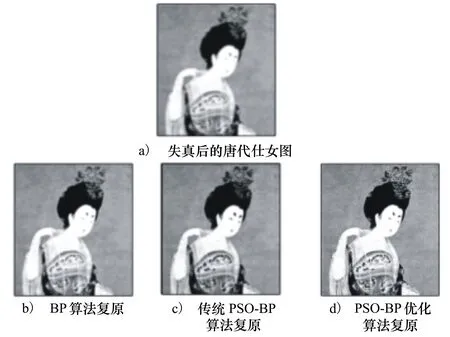
图7 唐代仕女图像复原效果对比
6 结 论
在本例的图像复原过程中,一方面采用粒子群搜索全局最优解对BP神经网络权阈值进行优化,并对BP算法自身进行优化;另一方面采用原始图像对PSO-BP优化算法进行直观校正,让复原图像尽量趋近于原始图像, 实现图像的最优化复原;最后再将这一最优化模式用于其他失真图像复原上。实验表明:反复利用粒子群优化BP网络的权阈值,可以得到更优的样本数据进行训练,再参照原始图像,对网络参数进行动态调整,就能快速得到更小的均方误差和,使复原图像更加精准。总的来说,PSO-BP优化算法比其他2种算法在图像复原上效果更好。

