面向行星滚柱丝杠副载荷均布的螺纹牙修形方法
郭辉, 佟瑞庭, 刘更, 张文杰, 马尚君
(陕西省机电传动与控制工程实验室(西北工业大学), 陕西 西安 710072)
行星滚柱丝杠副(planetary roller screw mechanism,PRSM)是一种可以将旋转运动和直线运动相互转换的机械传动装置。PRSM具有高速度、大推力和长寿命等优点,广泛应用于深海探测[1]、航空航天[2]、医疗设备[3]和高精密机床[4]等领域。PRSM工作时主要通过滚柱、丝杠和螺母之间的螺纹牙啮合进行运动和动力的传递,滚柱的两螺纹牙工作面承受交变载荷,尤其是在螺纹牙承载较大的情况下,更容易引起滚柱螺纹牙的疲劳破坏从而降低PRSM的使用寿命。
目前,国内外对PRSM的理论研究已经有较多的研究成果,但主要集中于运动学分析、接触特性、传动效率和摩擦力矩等方面,对PRSM螺纹牙载荷分布以及如何使各螺纹牙承载分布更均匀的相关研究还不够深入。杨家军等[5]分别计算了PRSM中的3种变形即Hertz接触变形、轴段变形和螺纹牙变形,建立了滚柱螺纹牙的载荷分布,并且得到了PRSM轴向静刚度。Jan等[6]将PRSM滚动体等效为受剪应力的矩形单元,建立了PRSM载荷分布计算模型,并与有限元结果进行对比。Jones等[7]利用直接刚度法建立了PRSM的弹簧刚度模型,且通过直接刚度法计算了螺纹牙的载荷分布,进而求出其接触应力,并分析了滚柱个数和螺纹牙个数分别对螺纹牙载荷分布的影响。张文杰等[8]综合考虑了PRSM轴段刚度、螺纹牙刚度和接触刚度以及安装方式、受力状态等因素,建立了PRSM载荷分布模型,并分析了安装方式、受力状态、结构参数和牙型参数等对PRSM螺纹牙载荷分布的影响。Lisowski[9]采用有限元法研究了PRSM滚柱与丝杠接触应力、螺纹牙轮廓优化以及丝杠与滚柱螺纹啮合及相关几何参数的问题。Abevi等[10]利用杆、梁和非线性弹簧建立了PRSM的载荷分布模型,并研究了滚柱弯曲变形对PRSM载荷分布的影响。张文杰等[11]从PRSM结构参数设计和螺纹精度设计方面展开研究,采用单因素方法研究了主要设计参数对载荷分布的影响规律,并得到了PRSM均载设计中设计参数优化的方法。Zhdanova等[12]通过使用2个弹性接触层的PRSM棒模型,求得PRSM螺纹牙载荷分布,并通过相关方程得出PRSM螺纹牙载荷分布与其几何参数、零件材料、加工精度以及啮合面间摩擦力之间的关系。上述文献研究了PRSM螺纹牙载荷分布不均并得到其分布规律。然而,如何通过改变螺纹牙结构形状,在满足螺纹牙强度的同时使得PRSM具有较好的载荷分布特性,达到螺纹牙承载均匀的目的,鲜有文献对其进行研究。本文考虑PRSM安装方式以及受力状态对载荷分布的影响,利用有限元方法对PRSM螺纹牙载荷分布进行分析,得到了螺纹牙载荷分布,并与文献[8]中得到的解析结果进行对比,以验证计算方法的正确性。在此基础上,分析了PRSM中滚柱与丝杠和螺母接触点变形关系,提出滚柱螺纹牙修形的方法,通过减小PRSM丝杠、滚柱和螺母的轴段变形,螺纹牙变形以及啮合点Hertz接触变形[8]的累积作用,从而使得PRSM螺纹牙承载均匀。在此基础上,对修形后PRSM螺纹牙载荷分布进行有限元数值计算,结果表明该修形方法能够明显改善螺纹牙承载状况,对提高PRSM的承载能力及使用寿命具有重要意义。
1 PRSM结构与载荷分布模型的建立
1.1 PRSM结构和安装方式
常用的PRSM主要有2种,分别是标准式PRSM和反向式PRSM。本文主要以标准式PRSM为研究对象,即将丝杠的旋转运动通过滚柱的自转和公转转换为螺母的直线往复运动。标准式PRSM的结构如图1所示,主要由滚柱A、丝杠B、螺母C、内齿圈D和保持架E等组成。

图1 PRSM结构示意图
根据PRSM螺母安装方式的不同,可将安装方式分为2类,即同侧安装和异侧安装。在同一种安装方式下,由于螺母承受载荷方向的不同,PRSM有2种不同的受力状态,如图2所示。
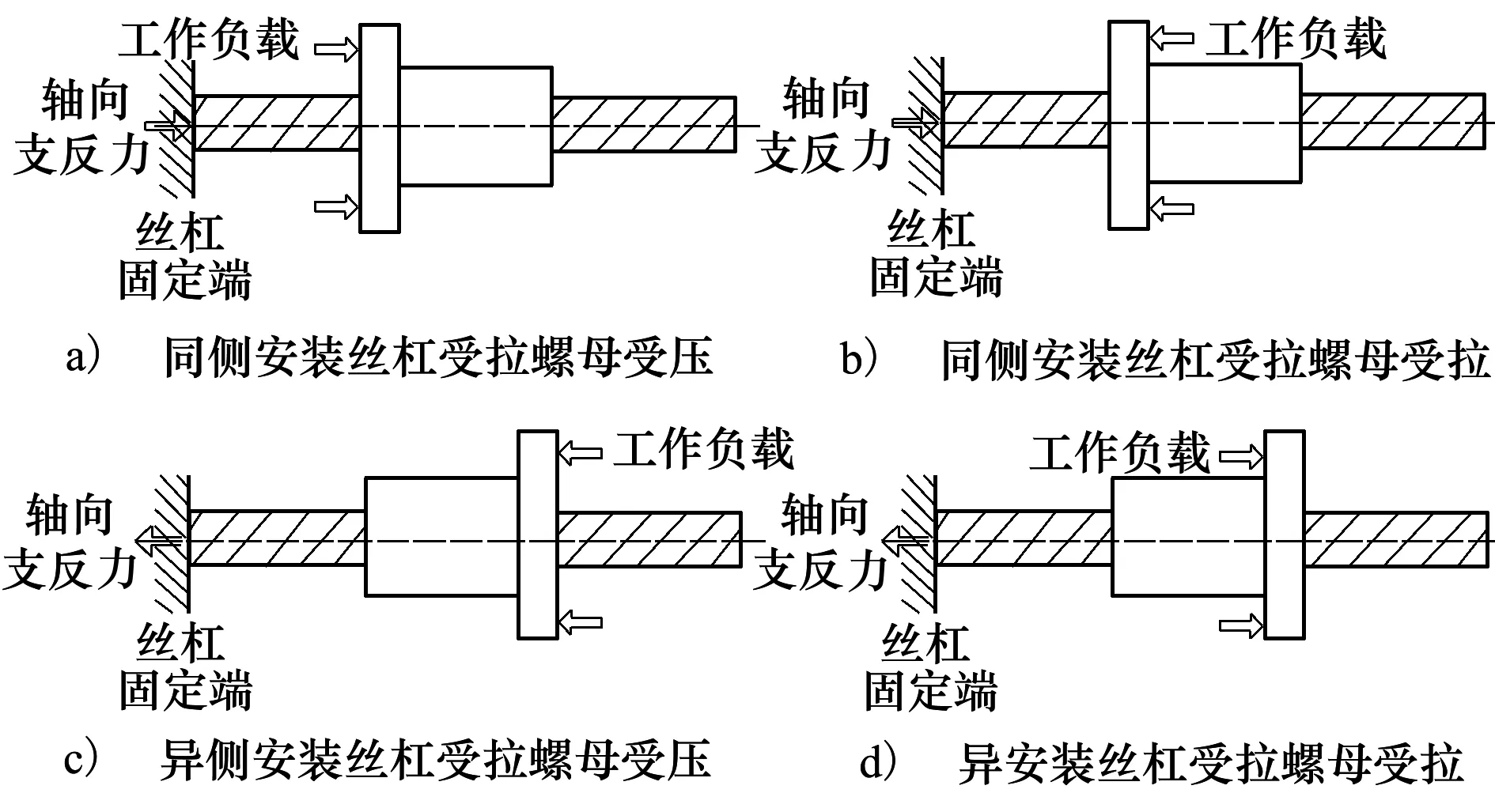
图2 PRSM不同安装方式及受力状态[8]
1.2 PRSM有限元模型
1.2.1 模型假设
由PRSM主要通过螺纹牙承载的特点,在建立PRSM有限元模型时,只考虑滚柱与丝杠和螺母螺纹啮合部分。在计算过程中,根据PRSM结构及承载特点,在有限元模型中作如下简化:1) 在有n个滚柱的PRSM中,每个滚柱承受载荷相同,因此,仅取整个PRSM结构的1/n;
2) PRSM中滚柱、丝杠以及螺母的材料各向同性。
1.2.2 网格划分
选取如表1 所示的结构参数建立PRSM三维模型。材料选用GCr15,弹性模量212 GPa,泊松比μ为0.29,屈服极限为1 617 MPa。在PRSM有限元模型中,由于丝杠和滚柱螺纹的螺旋升角不同,因而丝杠侧滚柱与丝杠接触点的位置会偏离丝杠和滚柱轴线所在平面。螺母和滚柱螺纹的螺旋升角相同,所以螺母侧滚柱与螺母接触点的位置则位于螺母和滚柱轴线所在的平面内。因此,对有限元模型中螺母侧和丝杠侧接触区域进行网格密化,如图3所示。接触区域采用八节点六面体非协调实体网格单元C3D8I,非接触区简化其网格模型以减少计算时间。

表1 PRSM主要结构参数

图3 PRSM有限元模型
1.2.3 边界条件
按照PRSM真实运动及受力状态,在对模型进行有限元分析计算过程中,需要对PRSM有限元前处理模型进行边界条件的施加。由于本模型是多体接触问题,因此为了提高其计算的收敛性,同时采用力边界条件和位移边界条件。位移边界条件设置为丝杠和螺母的两扇形面对称约束,螺母和滚柱只保留轴向自由度,丝杠端面固定。力边界条件为给螺母端面施加轴向载荷,本文所采用的PRSM(结构参数如表1),承载能力为5 t,滚柱数量为10个,因此,在螺母端面施加的载荷为5 000 N。
1.3 模型验证
采用与文献[8]相同的结构材料参数、安装方式及受力状态,得到不同安装方式下PRSM载荷分布的有限元解。定义丝杠侧接近固定支撑端螺纹牙序号为1,滚柱与螺母螺纹牙序号按照相同的方向定义。PRSM有限元模型载荷分布的结果与文献[8]进行对比,如图4和图5所示。
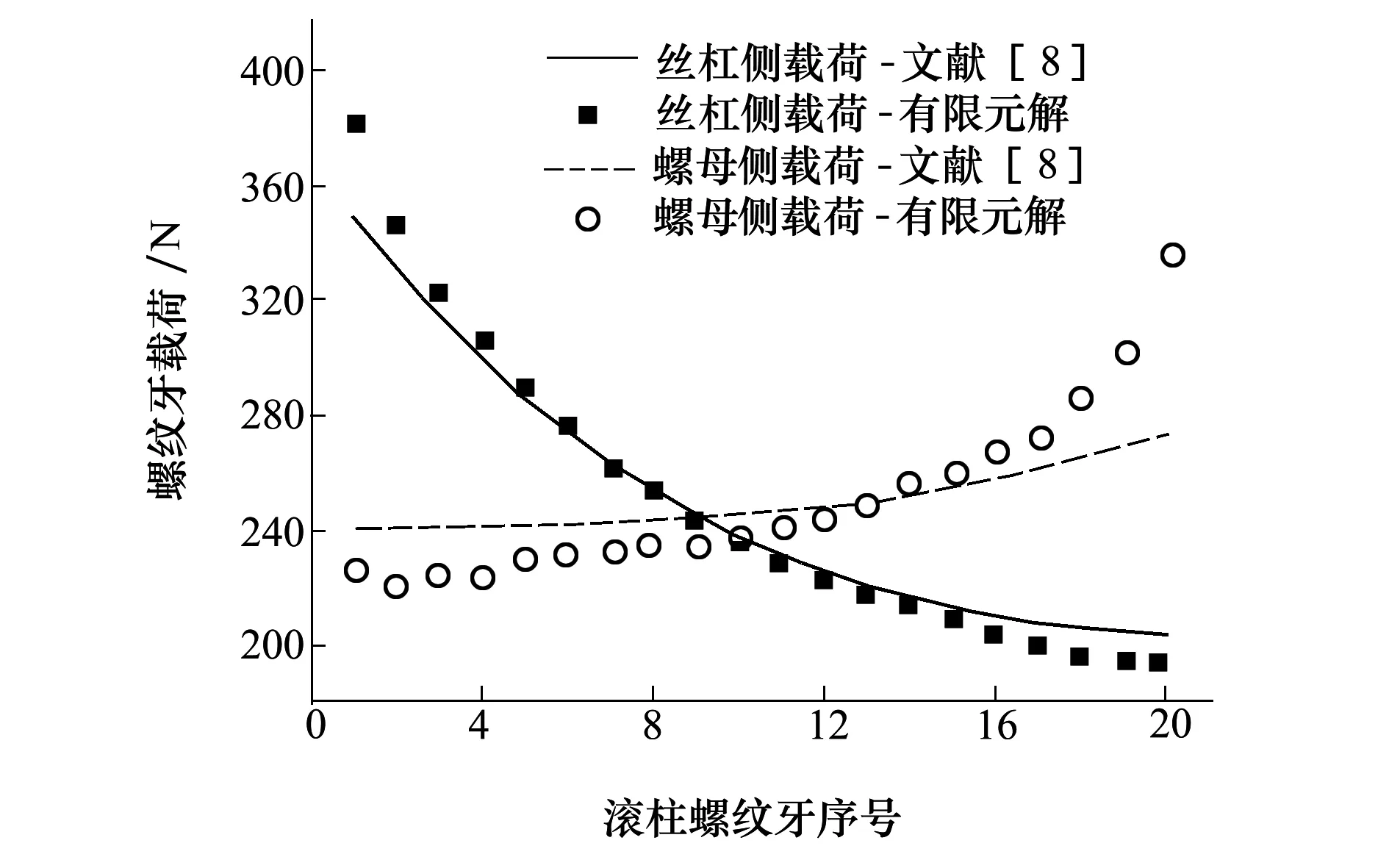
图4 异侧安装丝杠受压螺母受压
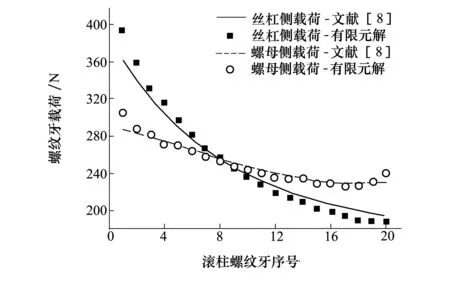
图5 同侧安装丝杠受压螺母受拉
由图4和图5可以看出,在PRSM不同安装方式及受力状态下,丝杠侧和螺母侧有限元模型载荷分布结果与文献[8]的解析解基本吻合,从而验证了该PRSM有限元模型载荷分布结果的正确性。
2 滚柱螺纹牙修形设计
由1.3节的模型验证结果可以看出,PRSM丝杠固定端和螺母承载侧的螺纹牙承受载荷最大,滚柱与丝杠接触侧螺纹牙承受载荷随螺纹牙序号的增加而逐渐减小。而滚柱与螺母接触侧螺纹牙承受的载荷在异侧安装时,随螺纹牙序号的增加而逐渐减小;同侧安装时,随螺纹牙序号的增加而逐渐增大。PRSM在高承载情况下工作,会造成滚柱承载侧第1个螺纹牙产生较大的载荷和接触应力,滚柱与丝杠和螺母螺纹牙承受载荷和接触应力较大,在循环交变的载荷和接触应力作用下,加速螺纹接触表面的粘着磨损,同时加快接触疲劳磨损,可能会引发最大承载螺纹牙的疲劳断裂,严重缩短PRSM的使用寿命。
基于上述结果,本文提出一种PRSM滚柱螺纹牙修形的方法,使得滚柱与丝杠和螺母螺纹牙接触时,各螺纹牙承受相同或相近的载荷。修形后滚柱能够有效降低PRSM螺母侧和丝杠侧螺纹牙承受的最大载荷,降低摩擦,减小磨损,进而提高PRSM的使用寿命。
2.1 滚柱螺纹牙修形方法
2.1.1 修形原理
通常为了提高承载能力和降低摩擦,滚柱螺纹牙端面设计成圆弧面[13]。图6为滚柱螺纹牙端面示意图,修形过程中保证滚柱螺纹牙端面轮廓形状不变,以图6中螺纹牙端面对称线为螺纹牙半牙厚变化的固定基准,丝杠侧滚柱螺纹牙半牙厚从丝杠的自由端开始沿螺旋线方向线性减小。同理螺母侧滚柱螺纹牙半牙厚从螺母的自由端开始沿螺旋线方向线性减小。滚柱螺纹牙半牙厚减小的最大值称为最大修形量。

图6 滚柱螺纹牙端面示意图
图7为修形前后PRSM螺纹牙轴向间隙变化示意图,其中粗横线表示滚柱、丝杠和螺母的轴段,竖线表示简化的滚柱、丝杠和螺母的螺纹牙,细横线表示在修形前后螺纹牙轴向间隙大小。可以看出滚柱螺纹牙修形前后PRSM螺纹牙轴向间隙发生了较大变化:螺母侧从自由端到加载端螺纹牙间隙逐渐变大,丝杠侧从自由端到固定端螺纹牙间隙逐渐变大。而滚柱螺纹牙修形方法的本质就是通过改变螺纹牙间的间隙,补偿由于承载后变形累积,进而减缓PRSM螺纹牙承载分布不均。

图7 滚柱螺纹牙修形前后轴向间隙变化示意图
图8为滚柱螺纹牙修形后PRSM承载示意图,修形后的滚柱与丝杠和螺母接触时能减少由于承载变形累积而引起的螺纹牙载荷分布不均匀,从而使得PRSM各螺纹牙承载均匀。

图8 滚柱螺纹牙修形后PRSM承载示意图
滚柱螺纹牙的修形是在已经完成加工的滚柱螺纹牙的基础上,通过砂轮磨削进行滚柱螺纹牙修形的精加工。在整个滚柱螺纹牙修形的过程中,通过改变砂轮的进给速度,即由正常的匀速进给变为匀加速进给。但是,滚柱与丝杠接触侧和滚柱与螺母接触侧承受的载荷方向不同,因而滚柱螺纹牙的修形过程中砂轮进给的方向也不同,且砂轮进给的速度也不相同。
在对滚柱螺纹牙的单侧进行修形时,假设滚柱的螺距为P,共有n个螺纹牙,且其旋转的角速度为ω,那么在已知最大修形量为Δx的情况下,可以推算出砂轮进给的速度和加速度,具体推导过程如下:
在每一个滚柱旋转周期内,砂轮进给的位移为等差数列,则砂轮从螺纹牙1到n总共走过的轴向位移s为
(1)
经历的总时间t总为

(2)
式中,T为滚柱旋转的周期
(3)
(4)
加工标准螺纹时,轴向进给速度v0为
(5)
那么加工完最大修形量时进给的速度vt为
(6)
所以进给的加速度a为
(7)
进给的速度为:
(8)
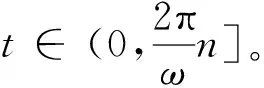
2.1.2 最优修形量分析方法
由于PRSM螺纹结构复杂,无法用解析方法对修形后PRSM螺纹牙承受的载荷进行准确的计算。因此,主要通过有限元方法计算得到PRSM修形后的螺纹牙载荷分布。本文在表1结构参数的基础上对PRSM中滚柱螺纹牙进行修形,主要以图2中的安装方式c(异侧安装丝杠受压螺母受压)为例,建立装配有修形后滚柱的PRSM的三维模型,在保证材料参数、边界条件等前处理方法与模型验证中的有限元模型完全相同的情况下,简化PRSM接触模型进行有限元分析计算。
由1.3节模型验证的结果中可以提取出滚柱、丝杠和螺母承载后的累积变形量。在螺母端面承载5 000 N的情况下,提取得到丝杠、滚柱和螺母的累积变形量分别为0.012 97,0.012 41和0.008 1 mm。在对修形后PRSM载荷分布分析的基础上,将滚柱的丝杠侧和螺母侧螺纹牙半牙厚的最大修形量定为0.002,0.004,0.006,0.008,0.010,0.012和0.014 mm,求得PRSM滚柱螺纹牙的载荷分布,利用统计学的方法得出在总承载5 t且沿螺旋线方向线性均匀修形时,PRSM中滚柱螺纹牙的最优修形量。
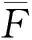
(9)
式中,Fi为丝杠侧或者螺母侧各螺纹牙上的载荷,i的取值为1, 2, 3, …, 19, 20。
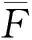
(10)
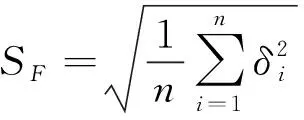
(11)
SF表示各螺纹牙载荷的均方差,表征各螺纹牙上的载荷偏离载荷平均值的程度,SF值越小说明各螺纹牙上的载荷越接近螺纹牙平均载荷。
2.2 修形结果分析
2.2.1 螺母侧承载结果分析
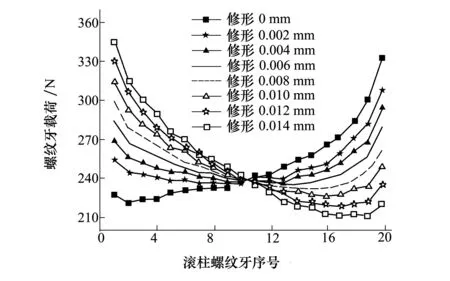
图9 螺母侧螺纹牙轴向承载
图9为滚柱修形量由0~0.014 mm变化的过程中螺母侧螺纹牙轴向载荷随螺纹牙序号的变化情况,可以看出随着滚柱螺纹修形量的增加,螺母侧螺纹牙承受载荷随螺纹牙序号增加的整体趋势由逐渐增加变为先减小后增加最后变为逐渐减少。
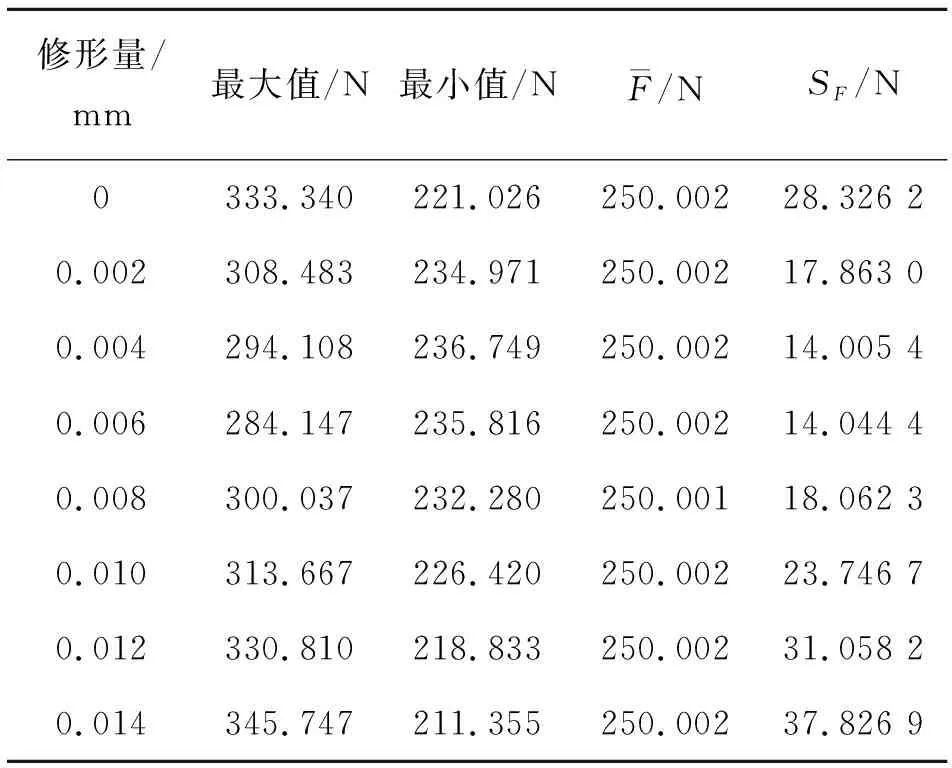
表2 螺母侧螺纹载荷随滚柱螺纹牙修形量的变化情况
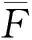
2.2.2 丝杠侧承载结果分析
图10为滚柱修形量由0.002~0.014 mm变化的过程中丝杠侧螺纹牙轴向载荷随螺纹牙序号的变化情况,可以看出随着滚柱螺纹牙修形量的增加,丝杠侧螺纹牙承载随螺纹牙序号变化趋势由逐渐减小变为先减小后增大。表3为丝杠侧螺纹载荷参数随滚柱螺纹牙修形量变化情况。

表3 丝杠侧螺纹载荷随滚柱螺纹牙修形量的变化情况
由表3可以看出,所列各修形量丝杠侧各螺纹牙的平均载荷均为250.001 N。修形量为0.012 mm时,SF为17.500 2 N是所列各修形量SF值中的最小值,说明在修形量为0.012 mm时,各螺纹牙之间载荷波动最小。此时,螺纹牙承载的最大值为292.469 N,是所列各修形量螺纹牙承载最大值中的最小值,螺纹牙承载的最小值为230.752 N,是所列各修形量螺纹牙承载最小值中的最大值。因此,可以得出在所列的各修形量中丝杠侧滚柱螺纹牙修形量为0.012 mm时各螺纹牙承载最均匀。

图10 丝杠侧螺纹牙轴向承载
从上述分析结果中可以看出丝杠侧载荷分布不均现象比螺母侧严重,丝杠侧较螺母侧分布更为不均主要是由于螺母的轴段刚度比丝杠侧大,轴段刚度越大,在相同的载荷下变形累积越小,螺纹牙载荷分布越均匀。丝杠侧和螺母侧对滚柱螺纹的修形量的敏感程度不同,螺母侧螺纹的承载较丝杠侧更为敏感。因此,本文在得到螺母侧和丝杠侧滚柱螺纹的最优修形量后,再将滚柱两接触侧的修形量分别设置为最优修形量,计算后得到最优修形量的螺纹牙载荷分布。
2.3 滚柱螺纹牙最优修形量分析
由2.2.1的分析可以看出,螺母侧滚柱螺纹修形为0.004 mm和0.006 mm时,螺母侧螺纹牙承载达到了较为均匀的状态,丝杠侧滚柱螺纹修形量为0.012 mm时,丝杠侧螺纹牙承载最均匀。因此,最终最优修形量滚柱应为螺母侧修形0.004 mm或者0.006 mm,丝杠侧修形0.012 mm,对其进行建模并计算得到2种情况下PRSM滚柱螺纹牙的载荷分布。图11和图12分别为螺母侧修形0.004 mm和丝杠侧修形0.012 mm时,滚柱螺纹牙载荷分布以及螺母侧修形0.006 mm和丝杠侧修形0.012 mm时,滚柱螺纹牙载荷分布图。
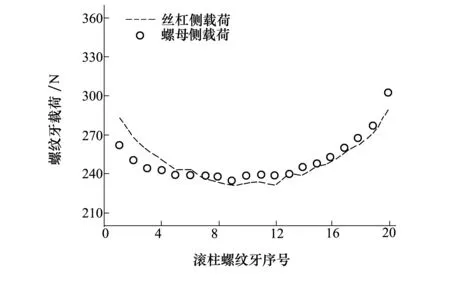
图11 螺母侧修形0.004 mm,丝杠侧修形0.012 mm时滚柱螺纹牙载荷分布
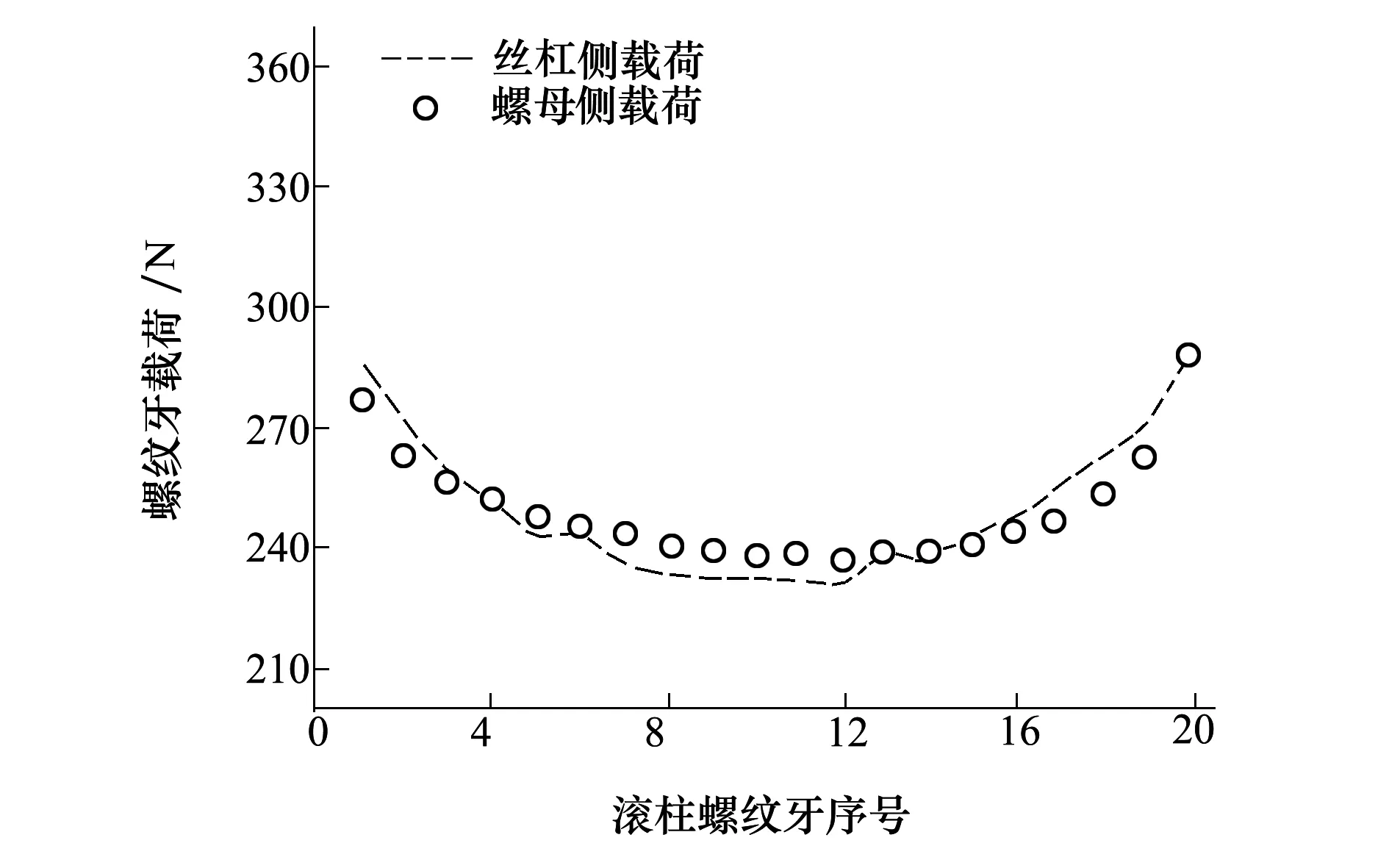
图12 螺母侧修形0.006 mm,丝杠侧修形0.012 mm时滚柱螺纹牙载荷分布

修形量/mm最大值/N最小值/NF/NSF/N0.004302.953235.419250.00216.400 5 0.006287.808237.294250.00213.482 6
对比图11和图12可以看出,修形后丝杠侧和螺母侧载荷分布都得到了优化,由表4可以看出当螺母侧修形量为0.006 mm时,SF值较修形量为0.004 mm时明显减小,说明各螺纹牙载荷更接近于载荷平均值,即螺母侧承载更加均匀,主要是因为丝杠侧螺纹承载对螺母侧螺纹牙的承载产生了一定的影响。因此,PRSM在异侧安装丝杠受压螺母受压的情况下,螺母侧滚柱螺纹修形量为0.006 mm,丝杠侧修形量为0.012 mm时,PRSM螺纹承载达到了最优,即各螺纹牙承载达到较为均匀的状态。
3 结 论
本文对不同安装方式下PRSM的螺纹载荷分布进行了有限元数值计算,并与解析结果进行对比,验证了计算方法的正确性。通过研究PRSM各种变形,提出了一种滚柱螺纹牙的修形方法。以某种参数的PRSM为例,在考虑异侧安装丝杠受压螺母受压的情况下,对滚柱两接触侧分别修形0.002,0.004,0.006,0.008,0.010,0.012以及0.014 mm后,计算了各种修形量情况下PRSM的载荷分布,研究了不同修形量对PRSM载荷分布的影响规律,得出以下结论:
1)丝杠侧载荷分布不均现象较螺母侧严重,主要由于螺母和丝杠的轴段刚度不同。丝杠的轴段刚度比螺母的轴段刚度小,轴段刚度小轴段变形累积越明显,载荷分布越不均匀。螺母侧螺纹承载和丝杠侧螺纹承载对滚柱螺纹牙修形量的敏感程度不同,滚柱两接触侧修形量为0.004 mm和0.006 mm时,螺母侧螺纹牙的载荷分布达到了较为均匀的状态;滚柱两接触侧修形量为0.012 mm时,丝杠侧螺纹牙的载荷分布达到了较为均匀的状态。因此,螺母侧螺纹承载较丝杠侧螺纹承载对滚柱螺纹牙修形量更为敏感;
2)对滚柱两接触侧修形量分别按照螺母侧0.004 mm丝杠侧0.012 mm以及螺母侧0.006 mm丝杠侧0.012 mm进行修形,并对修形后的PRSM载荷分布进行计算。结果发现螺母侧修形量为0.006 mm丝杠侧修形量为0.012 mm时,PRSM螺纹承载达到最优状态,说明这种均匀改变滚柱螺纹牙厚的滚柱螺纹牙的滚柱螺纹牙修形方法可以有效地改善PRSM螺纹承载状况,可以为未来高承载PRSM的设计提供理论基础;
3)对于不同型号参数以及不同承载状况的PRSM,其滚柱两接触侧(丝杠侧和螺母侧)的修形量不同,且(丝杠侧或者螺母侧)单侧修形量也不相同。未来PRSM均载设计时,可以通过对滚柱两接触侧修形量进行数值模拟,最后选出能够适应多种型号参数以及承载能力的PRSM滚柱螺纹牙修形量,拓宽PRSM滚柱螺纹牙修形的应用范围。

