一种高效准确的基于查询结果的基数估计策略

高锦涛, 李战怀, 刘文洁

(西北工业大学 计算机学院, 陕西 西安 710072)

基数估计是查询优化的重要组成部分，其效率以及准确性关系到优化器能否快速、准确生成最优执行计划。文献[1]中指出基数估计的错误率随着连接表的数量呈指数型增长，原因是中间结果的基数估计需要通过基本表的基数估计进行再推导得到。如果有多个连接，则存在多个迭代的中间结果，因此错误率被逐渐扩大。如果基本表的基数估计错误率较大，则严重影响查询优化的效果。

随着大数据时代的到来，数据库处理的数据量激增，在这种数据环境下，传统基于原表离线收集模式会大大降低数据的收集效率并增大基数更新延迟。而基于原表样本的收集模式虽然能够缓解大数据收集效率问题，但为保证准确度，需要较大的样本空间。一些策略[2-3]为避免从基本表推导得到基数，通过先前执行的一些查询的反馈信息或者通过执行当前查询的一些重要的子查询得到的结果作为基数值。这些策略虽然能够在查询运行时获得所需参数，但需要额外的查询执行代价，对于查询数据量很大的情况，代价较高。

本文提出一种高效准确的基于查询结果的基数估计策略，特点是维护一张基数表，基数表中的项(简称基数项)的内容为基本表或者中间结果在特定谓词下运行时得到的实际的执行结果的基数，保证基数的准确度。添加基数项热度、过期信息等内容，增加基数项的可操作性。通过动态感知缓存资源，将基数项合理分配到缓存中，降低统计信息延迟。

1 相关工作

关于基数估计的研究主要集中在不同架构下的基数估计策略以及不同查询阶段的基数估计策略。不同架构指集中式和分布式架构，不同查询阶段指查询编译期和执行期。基数估计分为统计信息收集、维护和使用3个阶段，下面就这3个阶段在上述2个研究方面上的不同实施策略进行阐述。

1.1 不同架构下基数估计策略

1.1.1 集中式架构

·收集阶段为处理大数据，集中式架构收集策略一般采用样本收集[4-7]。如postgresql[4]，可根据样本率调整收集数据量。Oracle[5]提供多种收集接口，如DBMS_STATS，允许用户规定统计收集的并行度、样本方法以及收集粒度。Teradata[6]规定初始样本率为2%，如果检测到收集的结果发生倾斜，则自动将样本率调整到50%。文献[8]给出了保证统计信息准确度的收集量。

·维护阶段对于收集完毕的统计信息，如果原始数据改变较大，则需要对统计信息进行维护，保证其准确性。通常做法为设置一个单独线程，如postgresql的collector线程，用来捕捉更新量，如果判断更新量超过某个阈值，则触发维护机制。

·使用阶段优化器基于统计信息评估计划优劣。优化器从存储统计信息的位置获取统计信息，如postgresql，Oracle等，将统计信息存储于系统表，使用时，直接从系统表获取统计信息。

1.1.2 分布式架构

·收集阶段分布式架构下统计信息收集手段包括：依赖中心控制节点收集和分布式节点收集。Orca[9]中统计任务发生在主节点的memo结构中，收集单位是memo[10]中的组，数据来自底层分布式架构。微软的PDW QO[11]，对每一个分布式节点执行SQL语句进行本地统计信息收集，并将收集后的统计信息存储在本地。文献[12]提出的解中心化统计方式，将数据路由到工作节点，由工作节点实时收集统计信息。文献[13]中统计信息的收集源来自内存，虽然收集速度快，但收集的量有限。

·维护阶段分布式架构下，统计信息维护手段与集中式类似，由更改数据量是否超过阈值触发收集任务。

·使用阶段分布式架构下，统计信息的使用方式主要通过局部统计信息推导出全局统计信息[9-11]。PDW QO[11]将存储在shellbase中的局部统计信息合并成全局统计信息。类似的，Orca[9]在生成父亲组的统计信息时，会给孩子组发送请求，由孩子组将各自的统计信息传递给父亲组，由父亲组合并成全局统计信息。文献[14-15]则利用不同的分布式节点交换统计信息。

1.2 不同查询阶段基数估计策略

基数为推导信息，来源于基本统计信息[16]。统计信息一般以直方图进行表示，对于直方图的详细阐述可以参考文献[17]。统计信息服务于优化器，目前常见的优化器工作阶段分为查询的编译期以及执行期，由于这2个阶段主要涉及统计信息的使用，因此这里只讨论统计信息的使用阶段。

1.2.1 编译期

·使用阶段查询编译器涉及到的统计信息为静态统计信息，获得手段为on-line模式[4-7](统计信息收集和使用在同一时刻)或者off-line模式[9-11](统计信息收集和使用分离)。这2种模式下获得的统计信息是静态的，不会根据执行时值的变化动态调整统计信息，维持准确性。

1.2.2 执行期

·使用阶段由于基数估计涉及的参数在执行期可能发生较大改变，因此基于静态基数估计的优化器通常得不到准确的基数。为使基数估计能够根据执行期实际运行结果进行动态调整，一些自适应策略[2-3]被提出。文献[2]中提出一种ASE(adaptive selectivity estimator，自适应选择度估计)策略，不需要进行离线的统计信息收集或者建立样本，而是根据子查询的反馈结果进行基数估计，具体策略为以一系列查询为基准，根据前置查询的执行结果自我调整后续查询的统计信息，进而提高基数估计的准确度。

1.3 讨 论

上述各种策略对于统计信息的使用是即时的，没有利用执行期查询执行结果提高收集统计信息效率以及准确度，并将其进行缓存，利于后续使用。虽然文献[2]能够在执行期收集，但面对大数据量，收集效率较低，影响查询性能。文献[3]提出的LEO(learning optimizer,自学习优化器)涉及的基数估计策略和我们提出的思想最为接近，监控并学习查询执行过程中的基数估计结果，用来提供后续基数估计的准确度，但没有进行资源感知以及查询结果的缓存。

2 相关定义

为便于理解论文提出的基于查询结果的基数估计方法，给出如下相关定义。

定义1基数项(CardItem)，存储基于查询结果的统计信息的最小单位，类似关系中一个元组，形式化表示为:Ci=(type,name,predicate,cardinality,expire,hot),键为:(name,predicate)，下文将Ci简写为(t,n,p,c,e,h)。参数解释如表1。

定义2基数表(CardTable)，用来存储各个基数项，形式化定义为Ct={Ci}。Ct可以以关系的形式进行存储，方便建立索引，加快Ci的获取速度。

表1 Ci参数介绍

3 基于查询结果的基数估计策略

3.1 架 构

如图1所示,传统查询处理过程:输入查询,解析器将查询转换为逻辑树,根据逻辑树进行查询优化,生成计划,执行计划并得到最终结果。

图1 基于CEQR的查询架构图

查询优化过程中,利用统计信息推导出基本表和中间结果的基数进行基于代价的查询优化。引入CEQR策略后,首先根据逻辑树执行基数键提取模块(3.2小节),得到基本表与其关联谓词的对应关系,形成三元组(t,n,p),其中(n,p)为基数键,然后根据基数键利用资源感知模块(3.3小节)查找对应的基数项(Ci)将Ci反馈给查询优化模块。基数表维护(3.4小节)的内容来自更新操作产生的更改数据以及计划执行的结果。

3.2 基数键提取

为方便分析,采用经典SPJ(select project join,选择,映射,连接)格式[18]作为对象。这里只针对基表(B)进行提取,中间结果部分在计划执行阶段通过基表推导或者从Ct中获取。提取过程如图2所示,{n1,n2,..,nm}为连接的基表,{p1,p2,…,pk}为选择谓词。以基表为单位,将属于这个基表的选择谓词映射到这个基表,然后形成一个三元组(t,n,p)。(t,n,p)为Ci的一部分,p为选择谓词构成的集合。如果p中某些子集能够合并,即这些子集中的元素涉及相同列的谓词,则将其合并成一个谓词。

图2 基数键提取

示例见图3,图3中,c1,c2表示表的列名。如p1(n1.c1<100)和p3(n1.c1>0)同时隶属于n1表的c1列,因此将这2个谓词合并,形成新的谓词:c1(0,100)。

图3 基数键提取示例

3.3 资源感知策略

随着硬件技术的发展,缓存资源越来越丰富,为

充分利用富余缓存资源,提高Ci获取速度,将热Ci映射到合适的缓存区。这里将Ci分为热Ci(Hot CI,简称Hot-Ci)、冷Ci(Cold CI,简称Col-Ci)和温CI(Middle CI,简称Mid-Ci)。Hot-Ci常驻缓存,Col-Ci常驻磁盘,冷热数据通过Ci访问频度进行标识。Mid-Ci指新生成的Ci,需要将它的键与缓存中Ci项的键进行比较确定其冷热程度。资源感知过程如图4,其中{k1,k2,…}表示Ct表中各个Ci的键值,对应定义(1)中的(n,p)。缓存中以Ci格式定义缓存项。如果存在相等的缓存项,则进行合并(合并方式见3.4节)。如果没有匹配,则标记为Col-Ci存储到Ct中。这里规定初始映射到缓存项的Ci为旧Ci(o),新生成的Ci标记为新Ci(n)。

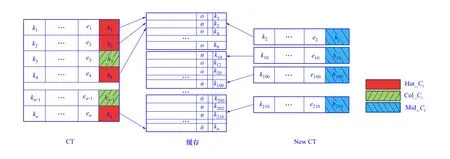
图4 资源感知过程

为合理安排Ci,提出如下资源管理方法。每一个Ci大小基本固定,设置为r,并规定缓存资源(Si)中Ci所占百分比为pi,则某一个缓存资源Si所能存储的Ci的个数如(1)所示。

(1)

利用(2)中的哈希函数根据Ci的键将其映射到合适的Si中,并保证按键排序,其中N表示Si的个数。如果某一个Si中保存的Ci个数违反公式(1),则利用线性探测再散列的方式找到其合适的存放位置A。

(2)

3.4 基数表维护

基数表(Ct)与基本表数据大小无关,但与基本表数据的内容和查询句式相关,即原始基本表数据改变或者查询句式改变,都有可能导致Ct的改变,即影响Ci的准确度,需要对Ct进行维护。维护内容分为两方面:更改维护(3.4.1节)和查询维护(3.4.2节)。

3.4.1 更改维护

数据库中insert/update/delete 3种操作会改变基本表的数据,间接影响Ct,为统一维护接口,将insert/update/delete 3种操作涉及的数据转换为(t,n,p,c)格式,(n,p)对应Ct中的键。其中c只针对insert操作。转换过程如下。

·insert转换:将insert中涉及到的插入值转换为谓词形式,即统计各个插入列对应的值的最大值、最小值以及行数(c),得出(t,n,p,c)四元组,其中p由插入的值中最小值和最大值形成的区间得到。

·update转换:将update中涉及到的更新谓词映射到需要更新的表中,形成(t,n,p)。

·delete转换:将delete中涉及到的删除谓词映射到需要删除的表中,形成(t,n,p)。

由于(t,n,p,c)对应的Ci可能已经存在,因此需要根据情况对Ci旧值和新值进行基于键的合并、删除、更新等操作。维护的情况共分为4种:旧键包含新键、新键包含旧键、新键与旧键相交、新键与旧键不相交。具体维护操作列表如图5,其参数介绍如表2。

具体维护策略为:如果n-n和o-n不相等,则将n-n对应的Ci直接插入到Ct中。如果相等,则根据新旧谓词的关系(图5中的第一列)分类进行维护。具体以图5中第三行为例进行说明。对于Ci的其他项e和h,分别设为默认值false和1。

·insert操作:首先利用me操作将新旧谓词合并成新的谓词m-p,然后运行add操作将新旧基数相加得到新的基数m-c。虽然旧Ci的基数发生改变,但仍然存在概率被使用,为增加命中率,这里并不舍弃这个Ci,而是利用upd操作以σ倍的m-c更新为新的基数,最后将新形成的Ci(n-n,m-p,m-c),利用ins操作插入到Ct中。

·delete操作:首先生成m-c,然后更新旧Ci的基数。

·update操作:直接将新形成的Ci插入到Ct中,原因是update操作对于重叠的谓词部分的更新并没有改变这个范围内的行数。

图5 基数表维护操作列表

3.4.2 查询维护

维护过程如图6所示,其中t1,t2表示基本表,J1表示中间结果,即表连接后的结果。为具体说明维护过程,以流行的流水线执行方式[19]为例,以左深树表示执行计划。构建操作包括:fetch(p),counter( ),join(n1,n2,p),update(n,p,c)。

fetch(p),作用是获取一行满足特定谓词的数据,应用在基本表(B)的取数据操作和流水线某一个步骤(连接)的取数据操作。counter( ),作用是统计基表或中间结果实际输出行数。join(n1,n2,p),作用是根据连接条件连接两部分数据,n1和n2可能是基本表,也可能是中间结果。update(t,n,p,c),将3.2节形成的(t,n,p)以及获得的基数c通过键(n,p)对Ct进行更新,更新过程详见3.4.1节。维护过程如下。

·在计划执行过程中,从根节点开始遍历整颗物理计划树,并根据每一个节点的执行结果获得基数。

·对于中间结果(J1),采取如下步骤获取基数:join->fetch->counter->update。

·对于基本表(t),采取如下步骤获取基数:fetch->counter->update。

·基数获取完毕后,通过资源感知模块(3.3节)将对应的基数保存到缓存或者Ct中。

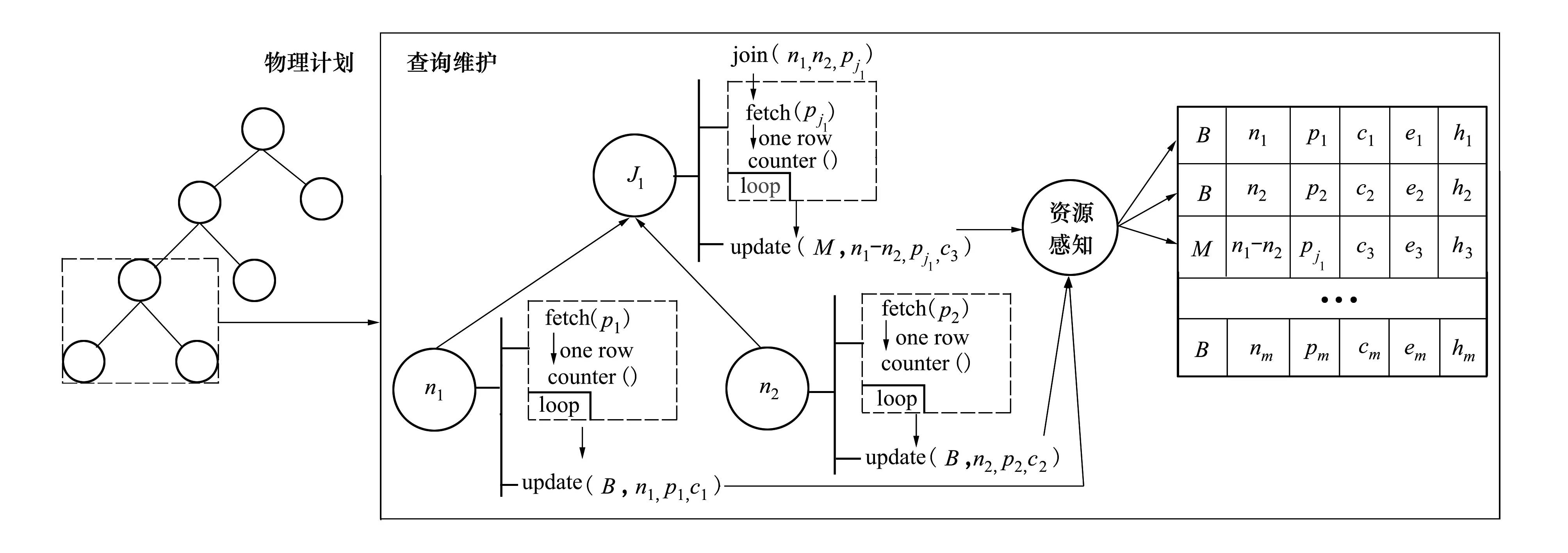
图6 查询维护过程

4 算 法

本章给出基于查询结果的基数估计策略(CEQR)算法伪代码描述。

CEQR算法

输入:Q,Ct,S

输出:{Ci}

1.A-tree=parse(Q)

2.B-keys=extract-keys(A-tree)

3.cards=get-cached-cards(B-keys,S)

4.IF NULL==cards

5. cards=get-basic-cards(B-keys,S)

6.P-tree=gene-physical-plan(cards)

7.{Ci}=collect-Ci(P-tree.root)

8.maintain-Ct({Ci},Ct,S)

CEQR算法对查询(Q)进行解析(parse),生成逻辑树(A-tree)(行1),利用基数键提取功能从逻辑树中提取基数项键值(B-keys,对应(n,p))(行2)。利用键值到缓存(S)中查找对应的基数(行3),如果基数不存在,则需要到基数表中查找基数(行4～5)。将得到的基数应用到查询优化中物理计划(P-tree)产生部分(行6)。在计划执行过程中调用collect-Ci函数从物理计划树中根节点(root)递归收集所有基表以及中间结果的基数(行7)。收集完毕后,调用maintain-Ct函数对基数表进行维护(行8)。

函数collect-Ci

输入:root

输出:{Ci}

1. IF root !=NULL

2. cards=execute(root)

3. IF root.type==B

4. {Ci}.push(B,cards)

5. IF root.type==M

6. {Ci}.push(M,cards)

7. collect-Ci(root.left-child)

8. collect-Ct(root.right-child)

函数collect-Ci用于根据执行结果收集基数。过程为:如果物理计划树根节点存在,则对于计划树中的每一个节点,根据执行的结果统计返回的行数(行1～2)。如果当前节点类型为基本表,则将基本表对应的基数存放到{Ci}中;如果为中间结果,则将中间结果对应的基数存放到{Ci}中(行3～6)。递归遍历左子树和右子树(行7～8)。

函数maintain-Ct

输入:{Ci},Ct,S

输出:Ct

1. FOR eachCiin {Ci}

2. addr=Hash(Ci)

3. old-Ci=fetch(S,addr)

4. IF old-Ci!=NULL

5. new-Ci=merge(Ci,old-Ci)

6. update(S,new-Ci)

7. store(new-Ci,Ct)

8. ELSE

9. store(Ci,Ct)

函数maintain-Ct作用为针对产生的基数项进行基数表的维护,过程为:对于每一个产生的基数项,计算其缓存地址,根据缓存地址获取缓存中已经存在的基数项(行1～3)。如果存在,则将其和输入的缓存项合并成新的Ci,更新本地缓存项,并存储到Ct中(行4～7)。如果不存在,则判断为冷Ci,直接存储到Ct中(行8～9)。

5 算法分析

传统基数估计步骤分为:统计信息收集(C)、统计信息获取(G)以及基数估计(E)。CEQR策略下,将基数估计分成基数键提取(De)、缓存查找(Fe)、Ci生成(Ge)、资源感知(Se)、基数获取(Eg)五部分。根据功能,有映射:(Ge,Se)->C,(De,Fe,Se)->G,Eg->E。下面就CEQR算法代价进行评估。

传统基数估计策略(TRA)估计时间代价见(3)式。其中T表示不同阶段的时间代价,t表示一次网络通信代价,N表示统计信息收集时需要进行的网络通信次数,与数据量成正比,M表示某个表数据分布的节点个数。

TTRA=TC+TG+TE

(3)

公式(3)中,无论是集中式(centralized)还是分布式(distributed),基数估计(E)都是在查询节点内存中操作,涉及数据量小,因此其时间代价可忽略(ignored)。统计信息获取(G)时,集中式下可忽略,而分布式环境下,由于一个表的统计信息分布存储,因此在查询节点获得统计信息时需要将局部统计信息进行整合,消耗网络代价。统计信息收集与数据量相关,在数据量较大时,需要消耗大量CPU代价(#CPU)和IO代价(#IO)。γ取值为{0,1},当收集统计信息时,需要形成全局和局部两种统计信息,则取值为1,代表消耗网络代价,如文献[20];当只形成局部统计信息,则取值为0,代表不需要消耗网络代价,如文献[21]。CEQR算法的时间代价如(4)式。

(4)

由于De和Eg都是在内存中进行,并且处理数据量很小,因此效率与E相当。Fe根据键到缓存获得Ci,如果命中(hit),则代价忽略,如果不命中(non-hit),需要消耗一次网络代价到Ct中获取Ci。即使分布式环境下,也不需要进行统计信息的合并,因此多数情况下不需要消耗网络代价。资源感知(Sw)策略作用是将热数据映射到合适的缓存资源中,分布式环境下需要消耗网络资源,与分布式节点数(K)相关。

综上所述,传统基数估计策略与原数据量相关,即使采用样本策略,为保证准确度,也需要在较大样本空间下进行。CEQR算法与原数据量无关,随着查询数量的增多,算法的准确度和效率大幅提升。通过(5)式的推导,得出TCEQR<=TTRA,等号成立的情况为在执行Fe时缓存不命中,随着查询数量的增多,这种情况将大大减少。

basedon:TDe⟺TE,TGe⟺TE,

TEg⟺TE,TFe≤TG,

TSe≤TG

infer:TCEQR≤TTRA

(5)

6 适应性

CEQR策略的效果会随着查询语句数量的增大而增强,并且随着硬件的发展,缓存资源逐渐丰富,能够充分满足CEQR策略的资源感知需求,大大降低统计信息的获取以及维护代价。因此CEQR策略能够满足OLAP、OLTP以及OLAP&OLTP系统中进行大数据量基数估计需求。

7 误差分析

定义3基数估计误差,即利用统计信息推导出的基数值和运行时实际基数值之间的差值。这里定义3种误差:初始误差(ΔI),表示计算基本表基数值产生的误差;连接误差(ΔJ),表示根据基本表推导出连接结果基数值产生的误差;更新误差(ΔU),表示原数据更新导致依赖的基数值过期产生的误差。这3种误差的定义以及关系如(6)式所示。VE和VA分别表示基数估计值和实际基数值。

ΔI|J|U=|VE-VA|

(6)

如果基数一经产生不会改变,则更新误差不存在,如OLAP系统。对于OLTP和OLAP&OLTP混合的系统,根据文献[1],ΔU加强(power)ΔI,而ΔI加强ΔJ,ΔJ则加强优化偏差。传统基数估计策略3种误差都存在,并且由于数据关联性以及样本建立策略的不合理,导致ΔI值较大,严重影响优化器的优化效果。基于CEQR的基数估计策略保存基本表和中间结果的准确基数值,因此大大降低了ΔI和ΔJ值。通过资源感知策略结合细粒度Ci,大大降低ΔU值。

8 实 验

8.1 实验环境

我们将CEQR策略实施在淘宝开源数据库——Oceanbase(源码见文献[22]，架构见文献[23])中。利用Oceanbase的单节点模式和集群模式搭建集中式测试环境和分布式测试环境。配置如下。

单节点模式 主频为1400MHz的AMD Opteron(TM)处理器和16G内存，物理CPU个数为2，物理核数8个，逻辑核数16个；操作系统为Red Hat 6.2。

集群模式 配置7个计算节点，其中1个主节点，6个副节点，主节点配置32G内存，其他和单节点模式配置相同，副节点配置全部和单节点模式配置相同。

8.2 实验数据

利用tpc-h工具[24]生成8组TPC-H相关数据集(每组包含8张表)，数据量为(0.5,1,5,10,15,20,25,30)，单位为Gigabytes。

8.3 实验结果

测试CEQR在单节点模式和集群模式下的效率。

8.3.1 单节点模式

在Oceanbase中实现postgresql的统计信息估计策略(简称PG)。目的为测试2种策略的统计信息收集效率，预期为CEQR收集效率高于PG。设置postgresql的样本率为30%。使用TPC-H相关查询Q4生成CEQR相关基数项。测试数据选取TPC-H中的ORDERS表，并保证CEQR和PG收集的数据量相同。测试结果如图7。PG中基数由统计信息推导得到，涉及到表行数，每列的不同值个数等统计信息的收集，需要进行各种聚集运算以及消耗数据扫描代价。而CEQR中基数来自SQL语句执行过程中表的实际基数，只需消耗基数计算的代价。因此CEQR收集效率优于PG。图7符合预期测试结果。

图7 单节点模式下CEQR和PG效率对比

8.3.2 集群模式

在Oceanbase中实现PDW QO中统计信息收集策略(简称PC)。PC利用SQL语句进行局部并行收集，虽然在一定程度上提高了收集效率，但由于存在倾斜问题以及合并全局统计信息存在的网络通信代价，因此预期数据量较大时，CEQR收集效率优于PC。测试结果如图8。

图8 集群模式下CEQR和PDW QO效率对比

图8中，当数据量较小时，由于子表分散比较均匀并且数量较少，因此PC的收集效率较高，与CEQR基本相同。当数据量较大时，由于负载不均衡以及网络通信的增加，使PC效率低于CEQR。图8符合预期测试结果。

9 结 论

基数估计在数据库查询优化中占有重要地位，其效率以及准确度关系最优计划的选择。传统基数估计策略中的统计信息或来自原数据或来自建立样本，是一种推导、估计的过程，不能真实反映运行时基本表以及中间结果实际基数，严重影响优化效果。论文提出一种基于查询结果的基数估计策略，能够在查询执行过程中保存准确的运行时基数，并利用资源感知策略，提供快速的统计信息获取以及维护，在查询量足够的情况下，能够大大提高基数估计的效率和准确度。