采用虚拟引力场的太阳帆/电推进混合推力机动轨道设计
孙冲, 袁建平, 方群, 崔尧, 汪明晓, 刘易斯
(1.西北工业大学航天飞行动力学技术国家级重点实验室,陕西西安710072;2.西北工业大学深圳研究生院,深圳518057;3.上海宇航系统工程研究所,上海201109; 4.国家航天局空间碎片监测与应用中心,北京100012)
连续小推力轨道设计在空间机动轨道设计方面有广泛的应用[1-2]。与传统脉冲推力或大推力相比,连续小推力轨道机动容易控制,机动能力强;另外其比冲小,实现轨道机动所需要的燃料很少,因而成为研究热点。文献[3]中,Mcinnes首次提出了使用太阳帆来改变引力场的大小,设计了悬浮轨道,并推导了实现悬浮轨道所需推力的解析解。Malcolm采用太阳帆产生切向固定推力,设计了从地球轨道到太阳极轨的转移轨道,解决了轨道优化问题[4]。然而,由于单独采用电推进或者太阳帆产生的推力较小,轨道转移常常需要很长时间。针对这个问题,Mengali等在文献[5]中提出了太阳帆和太阳帆/电推进结合的混合推进方法,并采用间接优化方法进行了轨道优化。在其文章中,太阳帆产生径向推力,用于改变引力场的引力常数,而与此同时电推进产生固定切向推力。在假定太阳帆能够产生50%的中心引力(μ2=0.5μ1)的条件下,混合推力能够减少燃料的消耗并且缩短空间机动任务时间。然而该方法是作为一种间接优化方法,并没有考虑推力约束问题,很难应用于实际空间机动轨道设计中。
本文针对连续小推力轨道设计问题,提出了一种基于虚拟引力场的混合连续小推力轨道设计方法[6-7]。该方法将虚拟引力场与平均算法结合,通过混合连续小推力形成虚拟引力场,进而采用平均算法求解在虚拟引力场下固定大小切向力作用下的机动轨道解析解。进一步,本文采用四阶龙格库塔积分方法分析解析解的精度,并提出了误差因子参数,从而保证解析解的精度。本文采用虚拟引力场方法,将航天器机动轨道设计优化问题转化成参数优化问题。该方法主要分为3步:①设计并优化满足任务约束(包括边界约束和推力约束)的虚拟引力场,以及固定切向推力的大小;②求解实现虚拟引力场的推力大小;③考虑太阳帆的动力学模型,求解采用太阳帆来实现虚拟引力场的控制律。
1 模 型
1.1 虚拟中心引力场的定义
虚拟中心引力场是指引力场中心不在地心上,且其引力常数不等于地心引力常数的中心引力场。该引力场可用参数(r0,μ2)来定义,其中r0为虚拟引力场中心与地心相对位置矢量,称为虚拟引力场位置参数;μ2为虚拟引力场引力常数[6-7]。
1.2 虚拟中心引力场下虚拟圆锥曲线轨道
根据虚拟中心引力场参数r0维数的不同,虚拟中心引力场可以分为2种,如图1所示;
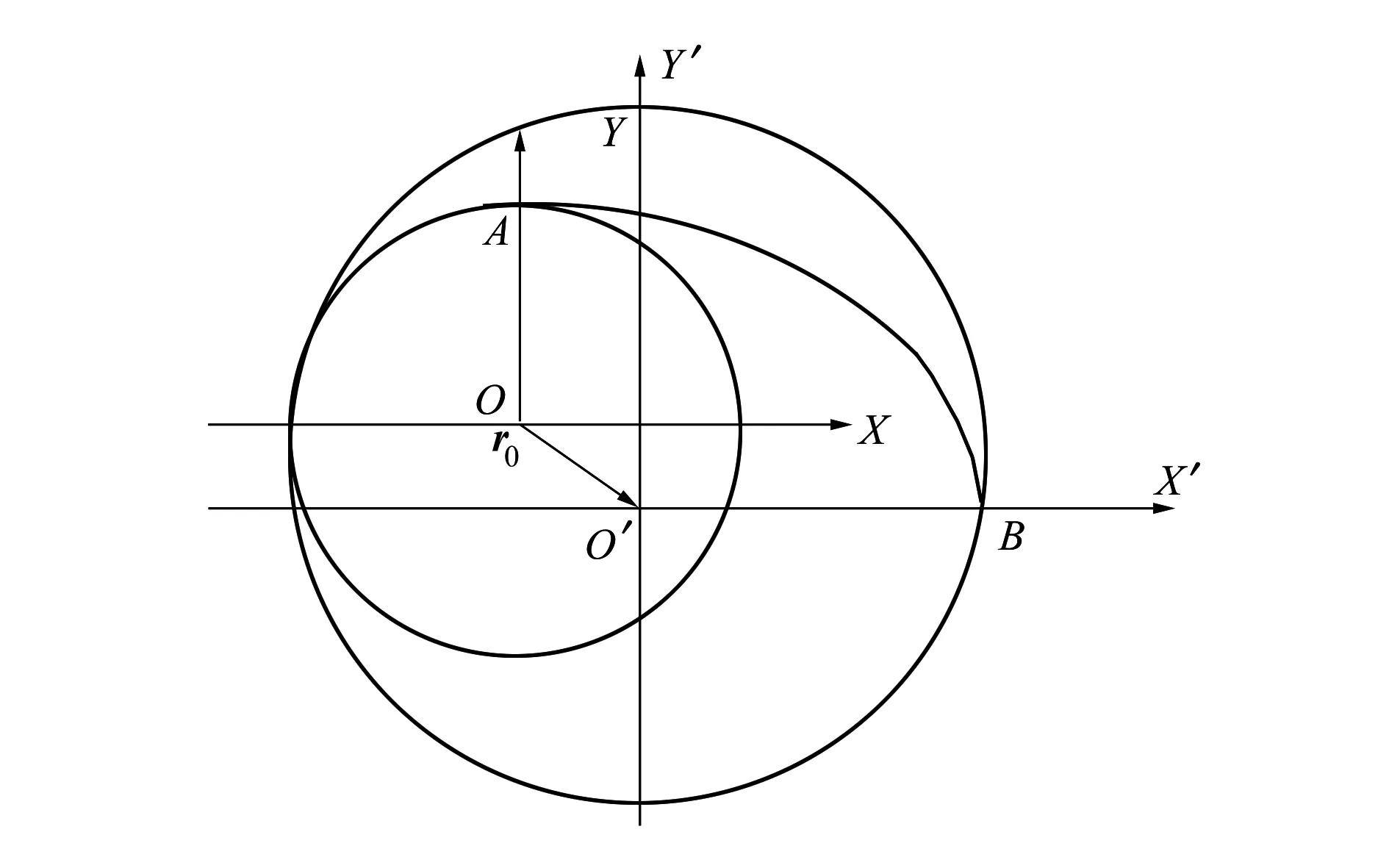
图1 虚拟中心引力场示意图
设定地心引力场引力常数为μ1,航天器在地心惯性坐标系下位置矢量为r1,假定在航天器上施加推力加速度为at,则有:
(1)
假设地心惯性坐标系为OXYZ,虚拟中心引力场坐标系为O′X′Y′Z。推力与地心引力场的合力形成的虚拟中心引力场参数为(r0,μ2),则在虚拟中心引力场坐标系下有:
(2)

(3)
由(2)式、(3)式可知,在虚拟中心引力场坐标系下,航天器运动方程可表示为如下形式:
(4)
实现虚拟中心引力场所需推力为
(5)
将(3)式带入(5)式, 可得
(6)
由上述分析可知,通过调整推力,可形成一种虚拟中心引力场。在该虚拟中心引力场中,航天器运动轨迹为圆锥曲线。若该虚拟圆锥曲线轨道满足轨道转移约束,则可实现轨道机动。
1.3 固定切向力作用下轨道摄动方程
在切向推力作用下,平面轨道高斯摄动方程为
(7)

(8)
径向推力以及周向推力和切向推力之间的关系为
(9)
而真近点角和偏近点角的关系为
(10)
因此,将公式(7)中自变量转换为偏近点角,则轨道半长轴和偏心率的变化[9]为
(11)
式中,E为偏近点角,ft为连续切向推力。在给定轨道交会的初始点A和终点B的条件下,采用混合推力方法设计机动轨道就是求解引力场参数(μ2,rvg)以及切向推力ft。若选择合适参数X=(μ2,rvg,fsep)时,在虚拟引力场中和切向推力的同时作用下,航天器在虚拟引力场可从A点转移到目标点B点,从而满足轨道交会的边界约束。这就是采用基于虚拟引力场方法的混合连续小推力轨道设计的基本思路。
采用虚拟引力场的混合连续小推力轨道设计方法来设计轨道,实际上是设计在虚拟引力场中的常值切向推力转移轨道。转移轨道需要满足两点边界值约束,以及推力约束。当初始轨道的偏心率很小,推力较小的条件下[9],在虚拟引力场中的切向推力轨道近似解析解为
(12)
当初始点和目标点已知时,上式中的参数E已知。边界约束可以转化为
(13)
由此可见,采用虚拟引力场下的连续推力轨道设计方法,可将所有满足边界约束的轨道用一组参数X=(μvg,rvg,fsep)表示,即转移轨道参数化。这样转移轨道设计与优化问题就可以转化成为参数设计与优化问题。
由上分析可知,采用虚拟引力场下的混合连续小推力轨道设计方法,需要给航天器施加推力,一部分推力用于形成虚拟引力场,另一部分推力用于形成虚拟引力场中的切向力。具体推力分配:将形成虚拟引力场所需要的连续推力与在切向力的合力分解为径向力和切向力,然后采用太阳帆和电推进分别产生分解的径向力和切向力。由公式(6)可知,实现虚拟引力场所需要的推力是有虚拟引力场参数决定的如下式所示,
Trvg=F(μvg,rvg,fsep)
1.4 太阳帆/电推进混合最近最优轨道设计
1.4.1 太阳帆推进模型
由公式(5)可知,实现虚拟引力场需要的力随着轨道半径的变化而变化。因而采用太阳帆来实现虚拟引力场,其推力大小和方向也都是实时变化的。在此采用太阳帆推进的理想模型[4]
Fsail=2PAcos2αn
(14)
式中,P=(S0/c)(r0/r)2,为太阳光压率。
采用理想推进模型,太阳帆产生的推力表示如下
(15)
式中,a1,a2,a3均为常数。而太阳帆产生的力在轨道的径向和切向的分量为
(16)
由此可知太阳帆推进可以实现部分径向和周向的正推力,而剩余部分需要用电推进来实现。
1.4.2 太阳帆电推进模型
本文选择文献[5]中的电推进器,其产生的小推力和电推进器功率参数相关,而需要的燃料消耗也由点推进器的功率决定。点推进器的功率是可变的,如公式(17)所示
(17)
则其产生的推力加速度在径向周向分量为:
(18)
1.4.3 推力分配
采用虚拟引力场混合小推力轨道设计方法设计轨道,需要推力来形成虚拟引力场以及在虚拟引力场中的切向力。本文采用太阳帆/电推进混合推力来实现虚拟引力场,并提供在虚拟引力场中的常值推力。由于形成虚拟引力场所需的径向力和周向力是固定的,而太阳帆产生的推力在径向和周向是耦合的,因此仅仅采用太阳帆无法直接提供形成虚拟引力场需要的推力。在此,本文在选择太阳帆的同时,另外选择安装2个电推进器,分别用于产生径向和周向的推力,使其与太阳帆光压推进产生的径向力和切向力相互匹配,共同作用产生形成引力势场,并提供常值推力。在此假定形成引力势场所需要的径向和周向的推力加速度为Tr,Tc,而太阳帆产生的径向和周向的推力加速度为assr,assc。电推进产生的径向和周向的推力加速度为asepr,asepc,则有如下公式
(19)
由太阳帆的数学模型可知,其产生的径向力和轴向力与太阳帆的位置和太阳帆姿态有关。采用虚拟引力场和常值推力结合的方法,其太阳帆的在每一时刻的位置是一定的,因此太阳帆产生的推力,实际上是由太阳帆的姿态角来确定的。为了能够最大程度利用太阳帆产生的推力,从而节省燃料,需要对其姿态角进行优化,在此假定太阳帆的姿态角α和轨道机动的转移角θ有如下的关系:
α=a2·θ2+a1·θ+a0
(20)
式中,a0,a1,a2为待优化的系数项。
当给定虚拟引力场后,轨道转移过程中需要电推进器产生推力的大小为:
(21)
对比本文与文献[5]可知,本文的推力分配与其不同。文献[5]中轨道机动的径向推力完全由太阳帆提供,而切向力由电推进提供。本文采用虚拟引力场方法设计机动轨道,太阳帆推力一部分提供径向力一部分提供切向力,这样可以减少电推进所需提供的推力。因而本文的推力分配方法比较灵活,可节省轨道机动所需燃料。
1.4.4 混合小推力轨道设计与优化
由上述分析可知,采用基于虚拟引力场的混合连续小推力轨道设计方法,可求出大量的满足边界约束的转移轨道,如图3所示。假定虚拟引力场参数以及切向力参数的参数范围为

图2 混合小推力轨道交会

图3 混合小推力转移轨道优化示意图
则轨道优化问题即可转化为参数优化问题,优化的参数为虚拟引力场参数和切向推力加速度,以及太阳帆光压推进的推力系数,而优化的目标函数可以为轨道转移过程中,电推进器消耗燃料质量:
J=min(mfuel)
(22)
式中,mfuel为任务结束时航天器的质量。
或是转移轨道的任务时间:
J=min(Tf)
(23)
或是同时考虑燃料消耗和飞行时间的权重函数
J=min(k1·mfuel+k2·Tf)
(24)
式中,k1,k2为权重,k1+k2=1。
结合上述分析可知,整体轨道设计流程包括以下几个步骤:
a) 给出初始轨道和目标轨道;
b) 给出满足推力约束的虚拟引力场参数范围和切向推力范围;
c) 在b)的范围中,选择虚拟引力场参数。
d) 将初始轨道状态(ri,vi)转化为虚拟引力
场中的轨道状态(rvg,vvg);
e) 优化切向力参数,求解满足边界约束条件的转移轨道;
f) 重复a)~e),得到大量的满足约束的转移轨道;
g) 采用Matlab软件中的Fmincon函数优化转移轨道。
2 误差分析
由第1节分析可知,采用虚拟引力场下混合连续小推力轨道设计方法,可求解出满足推力约束和边界值约束的解析解。然而在此需强调,公式(10)中的解析解是存在误差的。在此为了保证该解析方法的精度,本节采用四阶龙格库塔数值积分方法求解了轨道积分数值解,求出了解析解的误差。在此基础上,分析误差产生的原因并给出解析解的应用范围。具体的仿真条件见表1。
在此,将解析解的误差分为位置误差和速度误差,并分别用Δεr,Δεv表示
Δεr=ranslytical-rnumerical=f(x)
Δεv=vanalytical-vnumerical=g(x)
对比图4图5,以及公式(10)、公式(11)可知,解析解与数值解的误差和飞行时间、引力场参数、以及轨道参数有关。切向推力越大、飞行时间越长,该解析解的误差会越大;初始轨道(虚拟引力场中)的偏心率越大、半长轴越大其误差越大。这一结论也与文献[1]得出的结论一致。为描述解析解与数值解的误差,在此定义一个误差因子参数,如(25)式所示
(25)
对比公式(11)及(12)可知,解析解的误差因子会随着切向推力、轨道半长轴、轨道转移时间(偏近点角)的增大而增大,当(e<0.7)时,偏心率越大,误差参数越大。如图5所示,采用解析方法可以得到大量的转移轨道,同时采用四阶龙格库塔数值方法,就可以求解并分析这些解析解的速度误差、位置误差以及误差因子之间的关系。
以地球-火星转移轨道为例,采用虚拟引力场方法可以得到大量的转移轨道,在其中任意选择n条转移轨道(n=157)。采用数值积分方法,可以得出这些解析解的速度误差和位置误差与误差因子的关系,如图6所示。
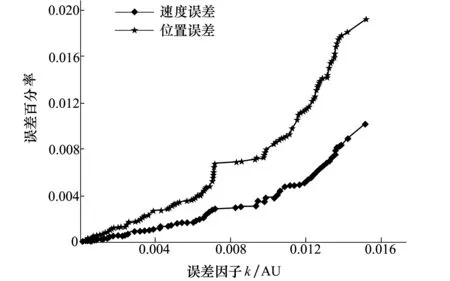
图6 速度、位置误差随误差因子的变化
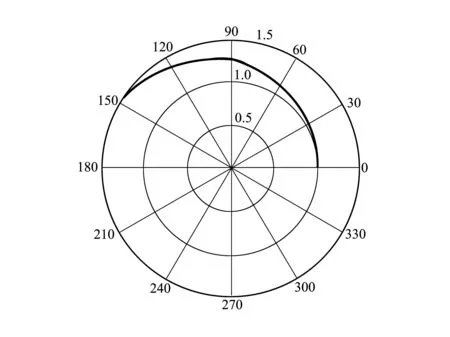
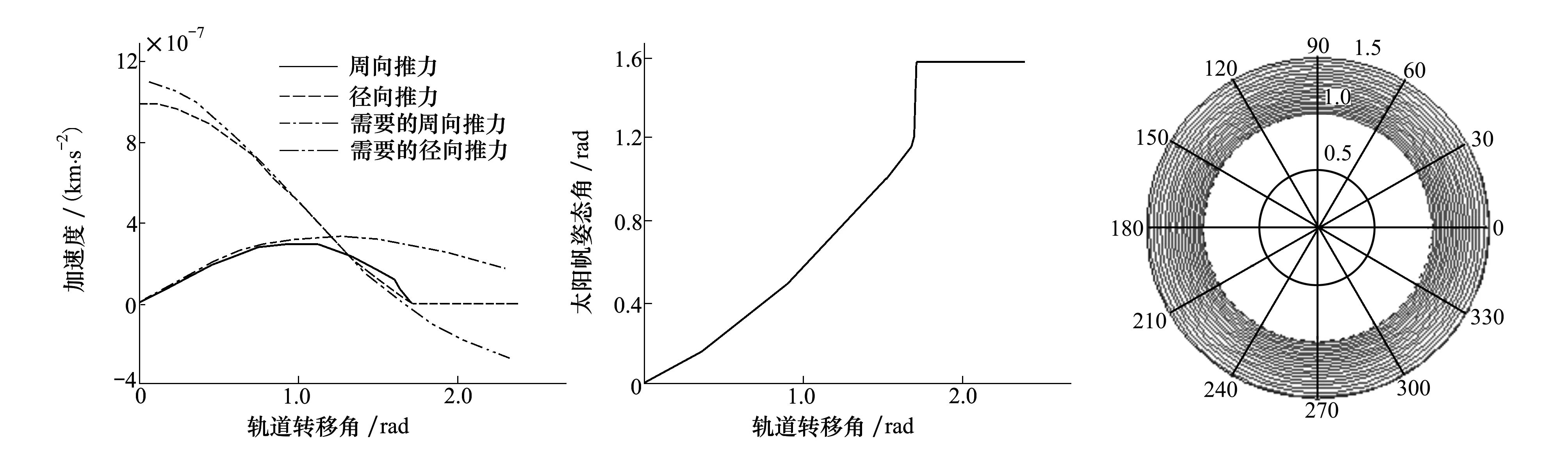
图6中,蓝色的线条为位置误差;红色的线条为速度误差;绿色的线条为误差因子。由图6可知,速度误差、位置误差和误差因子是同步的,当误差因子很小时,其对应的速度误差和位置误差也很小;相反,当误差因子比较大时,其速度误差和位置误差都很大。由图6可知,速度误差和位置误差都随着误差因子的增大而增大。当保证误差因子小于0.002 5时,速度误差小于0.001%,而位置误差小于0.002%。由以上分析可知,在采用虚拟引力场常值切向力解析方法设计转移轨道时,只需要保证误差因子k 表1 地球火星轨道转移虚拟引力场参数和常值推力 表2 太阳帆姿态角系数 图7 虚拟引力场混合推力方法的转移轨道 图8 切向推力方法的转移轨道(相同时间) 图7为采用虚拟引力场混合推力方法设计的转移轨道;图8为在相同转移时间条件下,采用常值切向力方法设计的转移轨道。图9表述转移轨道所需的周向推力和径向推力以及太阳帆提供的周向推力和径向推力。图10是转移轨道太阳帆姿态角。图11是为相同情况下(切向推力大小相等)得到的转移轨道。图12为实现虚拟引力场所需要的推力加速度。图13和图14表示推力秒流量和推力方向角。由表5可知,相比于常值切向推力,虚拟引力场混合推力方法能够很大程度上节省燃料,缩短时间。假定轨道转移时间相等,虚拟引力场混合推力方法所需要的燃料仅为常值推力方法的 。采用虚拟引力场混合连续小推力方法,所需要的电推进推力大大减小了,因而虚拟引力场混合推力方法能够扩大小推力轨道设计方法的应用范围。另一方面,在同样大小推力条件下,采用常值推力方法,需要的轨道转移时间和燃料消耗是相当大的。 图9 需要的推力和太阳帆提供的推力 图10 太阳帆姿态角图11 切向推力转移轨道(与电推进相同推力大小) 图12 电推进产生的推力加速度 图13 电推进需要的秒流量图14 电推进方向角 半长轴(AU)偏心率真近点角/rad真近点角/rad 初始值1000 目标值1.501.484(第一组)3.108(第二组) 表4 虚拟引力场参数和切向推力参数 表5 混合推力方法和切向推力力方法对比 本文提出了一种基于虚拟引力场的混合小推力设计方法。该方法能够以解析的形式求出大量的满足轨道边界约束的转移轨道,以及实现轨道转移所需的推力。同时,在给定目标函数的条件下,可对满足推力约束的转移轨道进行优化。与其它的小推力轨道设计方法相比,该方法有以下的特点: 1) 该轨道设计方法是一种解析方法,在保证精度的条件下,能够减小计算量,因而该方法可以为数值优化方法(直接法或间接法)提供轨道优化初值; 2) 与常值切向推力相比,该方法能够减小实现轨道转移所需的推力,扩大了小推力轨道应用的范围; 3)与常值切向推力相比,该方法不仅能够减小轨道转移所消耗的能量,而且能够减小轨道转移时间。 综上所述,相比于传统的小推力设计方法,虚拟引力场混合小推力方法,不仅能够节省燃料消耗,而且能减小任务时间,并扩大了小推力方法的应用范围。为小推力轨道设计与优化领域提供了新的思路。3 数值仿真

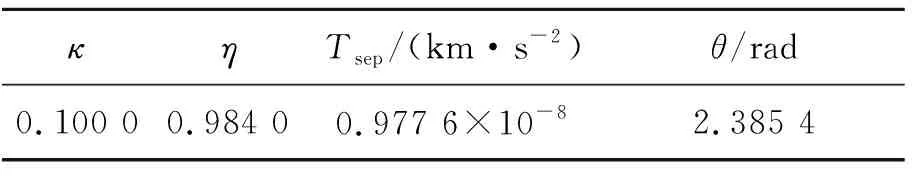






4 结 论

