基于裁剪分治的案例推理预测最近邻算法改进*

刘宝龙，胡楠楠，姚慧敏

(1.西安工业大学 计算机科学与工程学院,西安 710021;2.中国石油 长庆油田分公司第八采油厂,西安 710021)

伴随着复杂系统的发展，其研制、生产尤其是维护和保障的成本越来越高.以预测技术为核心的故障预测和健康管理[1-2]策略获得越来越多的重视和应用，发展为自主式后勤保障系统的重要基础.PHM 代表了一种方法的转变,一种维护策略和概念上的转变,实现了从传统基于传感器的诊断向基于智能系统的预测的转变,从而为在准确的时间,对准确的部位,进行准确而主动的维护活动提供了技术基础.PHM 技术也使得事后维修或定期维修策略被视情维修所取代[3].

案例推理[4]模拟人类解决问题的模式，在预测新问题时，先从案例库中检索出相似的案例，对其修正得到该问题的解.解决获取知识难的问题.基于CBR方法可以避开规则推理把案例分解成规则的难题，具有知识获取方便，容易理解等优点；利用历史案例的完全表达，求解过程简化；有效利用过去故障预测成功的经验和失败教训，可以在没有专家干预的情况下，增加新的案例，扩大求解范围.本文以陕西省咸阳市的威迪公司已经参与生产的高温真空压合机为研究对象，通过对现场设备运行状态的实时监测采集相应的生产数据，将CBR技术引入到设备健康管理[5]中，进行故障预测与健康管理，克服传统依靠人为维修经验不足的缺点，提高检修人员在故障诊断和维护水平，辅助检修人员做出正确决策.

案例检索是CBR的中心环节，其目的是从案例库检索出与目标案例最相似的案例，目标案例的诊断结果以及后期解决措施很大程度上依赖检索出来的案例的质量高低.CBR的检索出来的结果评价标准有两个要求：① 检索出来的案例与目标案例相似或者相关；② 检索过程中的案例匹配次数尽可能的少.

基于此，本文研究CBR中案例搜索的算法——最近邻算法，提出裁减分治思想实现，与最近邻算法实现的传统方法进行仿真实验，数据来源于已经参与生产的高温真空压合机.分析对比两种方法的效率、成本，并且测试随着案例库数量变化对两种方法效率的影响，并对算法进行改进，从而有效地提高产品装配系统的稳定性和可靠性.

1 最近邻算法原理

计算目标案例与源案例之间的相似度是整个CBR的核心，目前在系统中常用的检索算法为最近邻算法[6].最近邻策略原理是将目标案例划分到与其相似的大部分案例所在的类别，简单、 有效，但是当案例数量较多会导致计算量较大，计算时间较长.其基本思想是采用欧氏距离对两个实例进行计算，寻找最为邻近的解，从而达到对实例分类[7]的目的.

最近邻检索法将案例看作是在案例特征对应的n维空间上的点，新问题也描述成空间中的点，若一个案例有多个属性，将其每个属性值作为坐标值投影在n维空间中，利用建立的特殊查询结构可以迅速找到和新问题最佳的匹配点.本文仿真数据来源对象——高温真空压合机，采集设备实时运行数据，就有温度、真空度两个属性，每个属性取值间隔为10 s，获取到对应属性的属性值后，即可得到坐标，投影到二维空间.如图1所示,O为目标案例，案例库中的案例也均在属性空间内，找到距离最小的A即O在案例库中最相似的源案例.

图1 最近邻算法计算原理

该方法使用欧式距离衡量目标案例与案例库中的案例之间的距离[8].算法假设所有的案例都处于N唯的特征向量空间，每个案例X可以表示成特征向量[a1(x)，a2(x),…,an(x)]代表案例第K个特征属性值，则案例xi和xj案例之间的距离d(xi,xj)表示为[9]

(1)

式(1)一般适应于案例特征属性之间相关性比较强的情况.如果案例不相关性的属性较多，有些特征属性的影响可能要大一些，另外一些特征属性的影响要小一些，这样很难找到真正的“近邻”.通过对属性加入权重的办法可以很好地表现出属性的重要性[10-14]，经过加入权重后计算出来的案例相似度更接近实际情况.

2 实现方法

最近邻算法的效率与成本对CBR系统的影响是关键的，因此，如何实现最近邻算法且速度快和存储代价小是需要完成的目标.传统的最近邻算法都是循环遍历整个案例库，本文提出利用裁减分治思想实现最近邻算法.

2.1 循环遍历计算法

最近邻算法最常用的计算方法就是循环遍历.假设案例库中有N个案例，目标案例记为O，为了得到与O最相似的案例，就需用式(1)循环N次来计算目标案例与源案例的欧氏距离，用d(O，xi)表示xi与O的相似度.计算原理如图2所示.

图2 循环遍历计算原理

由此可以分析得出，循环遍历计算法的时间复杂度为T(n)=O(n)，空间复杂度为S(n)=O(1).理论上来说，传统的循环遍历法在时间和空间上均占有一定的优势，然而目标案例每次进行检索时，都必须对所有的源案例进行一一比较，此方法的检索时间会随着案例库数目的增加而同步增长.随着PHM系统案例库的不断丰富与完善，源案例数目越来越多，利用循环遍历检索会花费大量时间.

2.2 裁剪分治计算法

当案例库中案例数量达到一定数量值，遍历搜索会进行大量计算，因为无论案例库的规模大小，循环遍历会全部检索所有源案例，如何提高NN算法效率裁减分治计算法效率，可以从减小搜索区域入手，将搜索案例进行裁剪，达到提高效率的目的.

裁减分治计算法可作为一种使用多阶段决策过程最优的通用方法，原理是缩减搜索路径，从而达到提高搜索效率的目的.采用裁减分治方法的基本条件是案例库中所有的案例已经预排序，以链表形式存储.排序规则是以权重属性公式计算后的数值进行比较，假设系统有k个案例，每个案例有n个属性值，根据专家综合评定出每个属性的权重大小，使得n个属性的权值相加为1.再用式(2)计算权重属性数值后，进行排序：

(2)

式中：Valuek为第k个案例计算出来的权重属性值；xki为第k个案例中第i个属性值；ai为第i个属性的权重.

对高温真空压合机综合评定，一个案例共有两个属性分别为温度与真空度，其中属性权重分别为0.6和0.4，利用式(2)计算结果作为案例信保存在案例结构体中，并进行排序.算法处理过程如图3所示：① 以目标案例的权重属性作为分割线进行裁剪，将区域分割为S1，S2；② 以目标案例O在链表的位置，判断进行裁剪的区域.以图3(b)为例，S1、S2区域分别有9，7个案例，选择案例数较大的区域S1，在S1区域内进行遍历搜索，得出最小相似度，再以d大小在O左右进行裁剪.确定最终走索范围.③A有大概率的可能是最相似的案例，相似度为d.理想情况下在S2以d确定的阴影范围无更相似的案例，理想情况如图4所示，仅仅n/2次计算次数即可找到最相似案例.

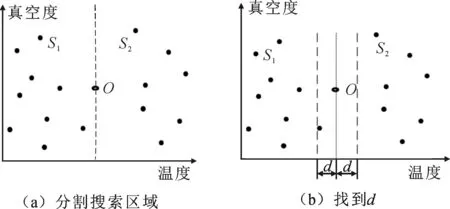
图3 裁减分治处理过程

图4中，如果阴影区域中无源案例，那么d是源案例距离目标案例O的最短距离，最小相似度也为d，与目标案例O最相似的源案例是A，检索成功.如果阴影区域中存在其他的源案例，那么它与O的距离必然小于等于d.而位于S2区域长为d，宽为2d阴影内，纵向围起来三根直线，将阴影区域划分为6个小矩形.设定S2区域内最小距离也为d，由此假设一个小矩形内有2个案例点，则两个案例点最远距离为小于d，与条件最小距离d矛盾，则由鸽舍原理可知，一个小矩形内至多有一个案例点.因此最多向前或向后尝试6个点，比较d与其与目标案例O的距离，就一定能找到最短距离，最终得出最相似案例大小.

以上方法，最理想状态是算法仅计算n/2+6次，即可得到最终值.而若遇到极限情况，S1与S2区域案例个数相差很大，算法依旧需要遍历近似n个案例才能得到最终结果，因此，分析可得本算法时间复杂度为T(n) = (n+n/2)/2=3n/4，相较于循环遍历法效率可提高25%.

图4 鸽舍原理计算

同理，当案例属性值为多个时，需要将其映射在n维空间内，以三维空间为例.目标案例位置x轴坐标m，现以平面：x=m将空间分割为大致相同的两个子集S1、S2，把求S中与O最接近点问题转化为求S1或S2中与O接近问题，假设S1空间中案例较多，一次遍历循环得到S1中距离O最短的源案例为A，距离为d，以平面x=m-d与x=m+d裁剪S1与S2后，如图5所示.

与二维空间类似，在S2中以平面x=m、x=m+d、y=d、y=-d、z=d和z=-d围城一个长方体去区间R，设A为最接近O的案例，则d×2d×2d这个区间中无其他案例存在，因此需要检索R中是否存在其他最接近案例.如图6(a)所示，利用鸽舍原理，R中存在的候选点最多为24个，每一个小长方体(d/2)×(2d/3)×(d/2)中最多只有一个候选点，如果有两个以上的点，设u和v是这两个点，则

(3)

图5 三维空间裁剪

如图6(b)所示，与d意义矛盾，因此最多可能存在24个这样的候选点，在分治过程中，最多向后检索24个点，即可找到最短距离.

图6 三维裁减分治

由图6可知三维空间裁剪分治法的理论时间复杂度为n/2 +24次，平均算法复杂度为3n/4即可找出最接近案例.与二维属性空间相同，最终算法相比传统遍历循环法可提高25%.对于二维三维的裁剪分治法描述，可推至多维属性空间，当属性有多个，同理可将案例属性映射在n维空间中，进行分割裁剪，最终算法时间复杂度均为3n/4.

3 实验结果与分析

仿真实验通过传感器采集实时高温真空压合机数据，提取温度，真空度作为案例属性，案例ID、设备号和故障信息存储于结构体中.案例结构说明见表1.

表1 案例结构说明Tab.1 Case structure description

实验采用VS2010进行模拟仿真，分4次实验，分别模拟循环遍历法、居中裁减分治、偏离70%和偏离90%裁减分治，每次分别获得案例库数目为100,200,300,…,2 000，共20个时间.

案例表示选择面向对象方法，利用类之间的继承关系，建立案例之间的层次结构，便于案例库的组织和检索[15].设备故障案例可以用一个四元组来定义

C=(D,S,M,E)

(4)

式中:D={d1,d2,…,dn}为非空有限集合，表示对设备故障案例的描述，包括设备编号，故障编号，故障发生地点，设备故障描述等；M为设备故障结论信息，包括处理方法、结果评价；E为设备案例的辅助信息；S={s1,s2，…，sn}为非空有限集合，表示故障案例的特征集，包括故障案例特征向量，案例特征权重向量.

案例库组织形式为双向链表形式，实验前提是所有案例库以“温度”属性由小到大排序进行链接.仿真试验结果如图7所示.

图7 仿真结果

由图7可知，当目标案例处于案例属性空间中段位置，循环案例方法的效率会随着案例数目的增加而近似线性增长，裁剪分治法也保持相同的趋势变化，而裁剪分治方法相比循环遍历方法，效率平均提高25.085 5%，与上述理论分析结果一致.为了测试裁减分治法在目标案例偏离多数案例时是否仍有理论效率，分别以偏移70%的目标，偏移90%的目标案例进行测试，从图中看出，裁减分治法的效率会随着目标案例偏离案例库的程度有所下降.裁减分治法的平均提高效率见表2.

表2 裁减分治法平均提高效率Tab.2 The efficiency increased by cutting and dividing method

由表2可知，当目标案例分别偏移案例库中心70%和90%时，裁减分治法的平均效率相比循环遍历法分别提高了14.481 4%和0.586 8%，目标案例是否处于案例库边缘对裁剪分治法的效率影响很大.当目标案例处于整个案例属性空间的外围时，裁减分治法与循环比例法效率差别不大.实际上，高温真空压合机的案例库具有一定的分布规律，案例属性空间比较集中.因此裁减分治法具有一定的优势.

4 结 论

本文对传统循环遍历法与裁减分治法进行理论分析与实验仿真，结论为

1) 在理想状态下，针对目标案例的搜索区域，采用裁剪分治法具有更高的搜索效率，效率提高了25.085 5%.

2) 目标案例在案例库中的偏移程度对裁剪分治法的效率影响很大.当目标案例处于案例库外围10%的区域，裁剪分治法与循环遍历法的效率并无大的区别.