一种改进粒子群的工业机器人时间最优轨迹规划算法

王玉宝,王诗宇,李备备,郭放达

1(中国电子科学研究院,北京 100043) 2(中国科学院大学,北京 100049) 3(中国科学院 沈阳计算技术研究所,沈阳 110168) 4(东北大学 计算机科学与工程学院,沈阳 110819) E-mail:wangshiyu@sict.ac.cn

1 引 言

智能制造已经成为时代发展的一部分.机器人是智能制造不可缺少的一部分,随着智能化的升级,对机器人提出了更高的要求,不仅要求机器人有更高的效率,还要求机器人工作性能的稳定.运动轨迹使机器人工作的重要组成部分,成为近几年研究的热点问题.论文中选取轨迹运动时间作为优化对象,基于改进粒子群算法完成对机器人时间最优轨迹规划.

常用的机器人时间最优轨迹规划[1,2]有遗传算法[3,4]和粒子群算法[5-9].其中,大多数轨迹时间优化问题采用遗传算法,部分采用粒子群算法.采用粒子群算法进行的研究虽然较少,但是也有一定的研究基础,论文中采用的动态学习因子粒子群算法正是在普通粒子算法优化的基础上展开的.

论文中选用PUMA560型关节机器人[10]作为研究对象,实验将以该款机器人的参数为准进行实验设计.论文中研究机器人点到点之间的轨迹.通过改进粒子群算法完成对时间的优化,找出时间最优运动轨迹.实验证明,改进粒子群算法动态调整粒子群算法中学习因子的取值,使群体在迭代初期能以较短时间搜索到最优值,迭代后期能够快速准确收敛到最优解.实验证明算法在机器人时间最优轨迹规划中得到很好的应用,显著提高了搜索精度,表明了模型和算法的有效性.

2 高次多项插值运动轨迹模型

为了保证机器人关节运动的平滑性,至少需要对运动位置R(t)施加至少四个约束条件,即初始时刻位置、终点时刻位置、初始时刻速度及终点时刻位置,这四个约束条件可以唯一确定一个三项多项式模型:

R(t)=a3t3+a2t2+a1t+a0

(1)

当需要引入加速度约束时,此时便需要用一个五次项多项式模型进行插值:

R(t)=a5t5+a4t4+a3t3+a2t2+a1t+a0

(2)

本文采用3-5-3高次多项插值的运动模型.高次多项插值的运动模型的核心在于将机器人运动轨迹分为三个区间,求取通过这三个区间对应时间最短的运动轨迹.假设机器人关节通过三个区间的运动位置分别为R1(t1)、R2(t2)、R3(t3),机器人关节在经过三个区间所用的时间分别为t1、t2、t3.则运动时间和运动轨迹之间的关系如式(3)-式(5):

(3)

(4)

(5)

通过式(3)-式(5)可以得出速度和加速度公式,将位置、速度和加速度公式联合可以求得高次多项式的参数.从而确定满足机器人运动轨迹的高次多项式.

3 简化粒子群算法模型

基本粒子群算法采用的是“速度-位置”的搜索模型来解决优化问题.每一个粒子均可以看作是解空间里面的一个潜在解,并通过解的适应值来决定该解的好坏.基本粒子群算法在初期具有较快的收敛性能,但随着粒子的同一化过程,往往容易陷入到局部最优.

为了取得全局最优解,胡旺等[11]人舍弃了粒子速度参数,进而改进了由粒子速度因素引起的迭代后期收敛速度及精度的降低的问题,但其没有考虑不同阶段学习因子的取值影响.本文在此基础上,根据不同迭代阶段,动态地调整学习因子,使粒子群避免在初期快速聚集阶段陷入局部最优,在全局进行大范围搜索的同时,保证在搜索后期也能快速找到全局最优解,动态的调节控制迭代前期的学习因子c1和后期的学习因子c2.

4 一种改进粒子群的时间最优轨迹

为了对关节型工业机器人进行时间最优轨迹规划,需要对粒子参数进行优化,求出各个粒子的最优解,从而获得整个优化过程的最优解.如上一节所,定义工业机器人关节通过各个区间的时间为分别为t1、t2、t3,随机取一组时间组合(t1,t2,t3)作为时间粒子参数,之后再随机取得多组时间粒子组合.式(6)所示θ(t)为时间粒子参数的表示函数:

θ(t)=min|t1+t2+t3|

(6)

通过式(6)中的时间粒子参数函数,我们可以计算出每组时间粒子参数的适应度.时间粒子参数的局部和全局最优解需要根据公式(7)-式(11)和公式(6)共同计算比较获得:

v[m]=w*v[m]+c1*r1*(pBest[m]-present[m])+c2*r2*(pBest[m]-present[m])

(7)

present[m]=present[m]+v[m]

(8)

W=Wmax-(Wmax-Wmin)*(n/N)

(9)

(10)

(11)

本算法中学习因子采用动态变化的学习因子,使用式(10)和式(11)确定学习因子.全局学习因子随着搜索次数的增加逐渐减小,局部学习因子随着搜索次数的增加而增加.通过动态变化学习因子使得搜索前期快速到达全局最优,而后期快速到达局部最优,提高了搜索效率,也改善了结果出现局部最优解不足.

5 实 验

5.1 实验设计

实验设计基于PUMA560进行,PUMA560是一款六自由度的机器人,关于该款机器人的相关信息可以通过文献[10]了解.通过对PUMA560型进行详细的运动学分析,使用MATLAB仿真工具箱进行仿真实验设计.

为了确保机器人末端抓手可达笛卡尔空间坐标,对机器人进行正向运动学求解,得到其起点的空间坐标位置和终点的空间坐标位置.得到机器人起点位置和终点位置后,再调用MATLAB中机器人库函数ctraj()求出两个插入点.最终获得机器人运动轨迹的三个区间及四个路径点,如表1所示.

表1 机器人末端运行轨迹坐标Table 1 Running track coordinates of robot end

通过笛卡尔空间坐标点逆解求得各个关节运动的位置,其中三个机器人关节对应的四个路径点空间位置关系如表2所示.

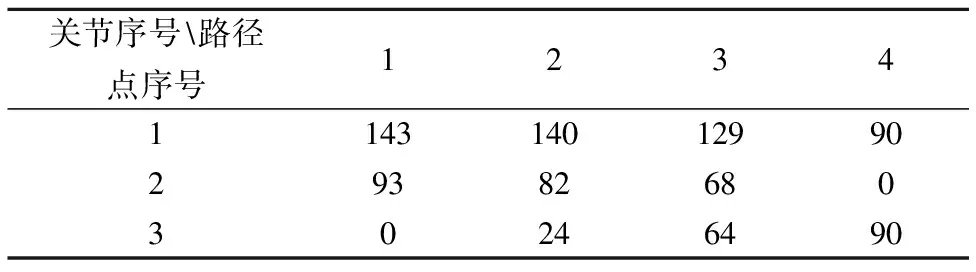
表2 路径点对应的关节解Table 2 Joint solution corresponding to the path point

实验过程中不仅需要考虑到粒子群算法中设置的条件,还要考虑工业机器人工作的常规条件,不能超出机器人工作的正常范围.根据公式(1)-公式(3)可以求出速度公式,利用速度公式可以验证是否满足式子(10)设定的约束条件.

(12)

优化过程,首先从二十组粒子中通过比较适应度值获取全局最优粒子.通过N次迭代不断更新粒子,计算出添加了约束条件后的最优解粒子,该粒子即为最优时间粒子.

5.2 实验验证与结果分析

实验中对机器人各个关节加入速度和加速度约束,通过简化粒子群算法模型进行实验得到如下结果,改进粒子群算法的优化时间收敛图如图1所示.从图中可以看出,在实验过程初期阶段,粒子群体能够在较短时间内搜索到最优的值,同时也能保证在后期快速准确的收敛到最优解.

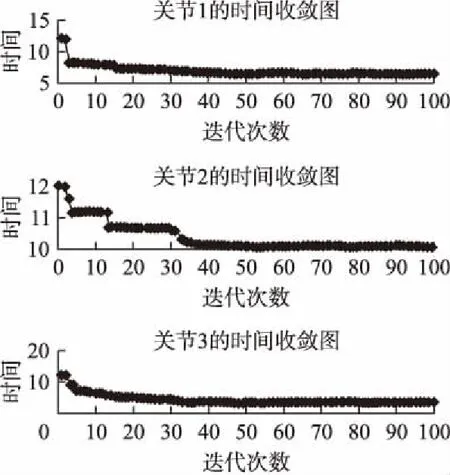
图1 时间收敛与迭代次数变化关系图Fig.1 Relationship between time convergence and iteration number

基于动态调整学习因子的粒子群算法完成优化,以机器人其中一个关节为例得出优化后的结果,并将未经过优化的关节时间解作为比较值同优化后的结果进行比较.

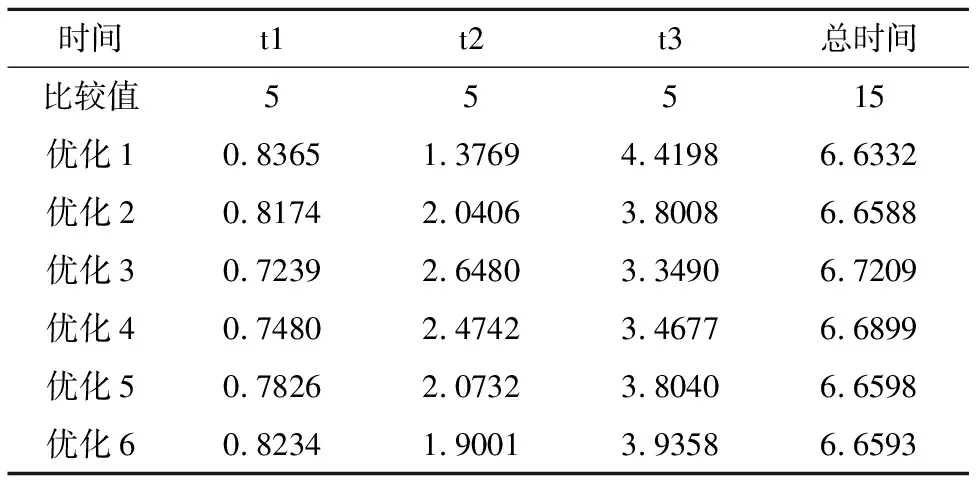
表3 优化结果Table 3 Optimization results

分析表3中的数据可以看出优化前和优化后有明显差距,优化前需要15秒才能完成,优化后只需要6.7秒左右就可以完成.轨迹运动时间缩短了约50%.达到了预期的目的.

图2(a)所示为沈阳高精数控公司研发的6轴通用型关节机器人LT-JRB03,其具有最大532mm的工作半径,能够负载3公斤的重量.该款机器人具有良好的运动性能,目前已经广泛运用于搬运、分拣及机床上下料等多个工业生产应用.

图2(b)所示为JRB03型关节机器人配套的控制器及示教器,将优化算法运用到图2(b)所示的实际机器人控制器中,图2(a)所示的机器人能够完成预期的运动轨迹.此外,基于Matlab的仿真实验及实际机器人环境运行均验证了本文提出的改进粒子群算法在工业机器人运动轨迹时间优化问题中的可行性.

将优化算法运用到图2(b)所示的实际机器人控制器中,图2(a)所示的机器人能够完成预期的运动轨迹.证明了本文所提算法的可行性.

图2 工业机器人及其控制器Fig.2 Industrial robot and its controller

6 总结与展望

本文采用简化粒子群模型与高项式插值模型对粒子群算法学习因子进行动态调节,进而对工业关节型机器人轨迹规划进行时间性能上的优化,轨迹运动时间缩短了约50%,达到了预期的优化目的.与其他算法相比,论文中设计的算法不仅结构简单、易于实现,并且能够能在较短时间内快速搜索到最优值和快速准确收敛到最优解.结果表明,论文中的算法模型能够完成对机器人运动轨迹的优化和实际性能的改善.

论文基于动态变化学习因子的改进粒子群算法完成了预期优化,但是还有需要深入研究和探讨的部分.如如何确定关节运动速度能够使收敛速度更快,时间更短;约束速度和加速度在什么条件下能够使轨迹运动时间更短等都是下一步可以研究的内容.