联合字典鲁棒稀疏表示的多聚焦图像融合

杨 勇,吴嘉骅,黄淑英,阙 越

1(江西财经大学 信息管理学院,南昌 330032) 2(江西财经大学 软件与通信工程学院,南昌 330032) E-mail:greatyangy@126.com

1 引 言

由于CCD设备中的光学透镜的景深有限,光学成像系统通常无法获得场景中所有目标都聚焦的图像.这一问题可以通过图像融合技术,更精确地来说是多聚焦图像融合技术来解决,该技术能将具有不同焦点的多幅图像融合成一幅所有对象均完全聚焦的图像[1].融合结果可以更准确、全面地描述图像的场景,有效地提高了多聚焦图像的利用率.

近十年来,多聚焦融合技术发展迅速,现有的融合技术通常分为空间域的方法和变换域的方法.空间域的方法拥有直接融合源图像聚焦区域的优点,但是高度依赖于清晰度测量标准的选择,比如图像的梯度能量、标准差或空间频率等[2,3].由于结构信息不能由单个像素来表示,基于区域的融合方法可以有效地从源图像中提取聚焦区域.Li利用抠图技术,来获得每个源图像的聚焦区域[4].然而,由于抠图技术的性能不稳定,该方法所得到的聚焦区域的边界并非完全可靠.考虑到相邻像素的灰度相似度与几何相似度,Kumar使用了交叉双边滤波器对多聚焦图像进行融合[5].然而,这种技术的普适性不能令人满意,因为该方法的滤波窗口的大小不能自适应地调整.近几年来,许多基于梯度信息的空间域融合方法被提出[6-8].这些方法克服了融合图像的块效应,但是融合的结果不稳定,边缘的过渡也不自然.

基于变换域的融合方法通常将源图像转换到另一个频率域进行处理,这使得源图像可以被有效地融合[9].这类融合方法的关键在于图像多尺度分解工具的选取和融合规则的制定[10].然而,现有的方法并不能表征图像的所有几何特征.举例来说,虽然小波变换[11]、轮廓波变换[12]、曲波变换[13]和剪切波变换[14]可以很好地表示各自的结构信息,但也只能提取有限的方向信息,不能精确地提取完整的轮廓.这将导致伪吉布斯现象等影响图像融合效果的副作用产生.虽然非下采样轮廓波变换(NSCT)具有良好的平移不变性,避免了伪吉布斯现象[15],但这种融合方法的计算复杂度非常高,占用内存较多,运行时间过长,限制了该方法的实际应用[16].此外,在图像逆变换的过程中可能导致一些有用的源图像信息丢失,对最终的图像融合效果有一定的影响.

卷积神经网络(Convolutional Neural Networks,CNNs)是近年来十分热门的一种深度学习模型,也是第一个在图像领域各个方面真正获得成功的深度架构[17].文献[18]首次将卷积神经网络应用于多聚焦图像融合,该方法利用清晰图像以及模糊图像训练卷积神经网络,并通过该网络得到融合决策图.但由于该方法是对图像块进行标记训练,可能导致聚焦与非聚焦区域之间的边界不准确.与卷积神经网络类似,由于在图像去噪、图像分类、人脸识别等方向上的成功应用,稀疏表示(SR)成为近年来计算机视觉领域的研究热点之一[19].在图像融合领域,SR也得到了充分的应用.文献[20-23]提出了多种基于稀疏表示的图像融合方法,通过建立特征与稀疏系数之间的关系来表示图像的显著信息.然而基于SR的传统融合方法存在3个主要缺点:1)对细节的保存能力有限;2)对图像未配准有很高的敏感性;3)稀疏系数无法准确判别聚焦区域[24].而这3个问题在多聚焦图像融合中是非常重要的.文献[25]提出了一种鲁棒稀疏表示模型(RSR)和多任务鲁棒稀疏表示模型(MRSR).不同于传统SR模型,RSR通过分解得到的重构误差作为图像聚焦区域的判别依据,得到的聚焦区域更加准确.MRSR方法对RSR进行了改进,该方法中每个图像块以及其相邻区域的信息被协同地用于确定多聚焦图像中的聚焦和非聚焦区域,这使得融合方法的鲁棒性大大提高.然而上述两种方法均使用单个源图像构建字典,容易导致字典的完备性不足.并且这两种方法抛弃了RSR分解得到的稀疏系数,仅使用重构误差作为判别依据,这将使稀疏系数中包含的聚焦区域信息被忽略,容易将非聚焦区域误判为聚焦区域.同时,MRSR方法的计算复杂度高,对聚焦区域的边界也未作进一步处理[25].为解决以上问题,本文提出了一种基于RSR和形态学滤波相结合的多聚焦图像融合新方法.与文献[25]中的RSR融合方法不同,源图像通过基于联合字典的RSR模型得到稀疏系数和重构误差,并通过两者共同判别图像的聚焦区域,以此获得初始的融合决策图.接着使用形态学滤波与高斯滤波优化初始决策图,从而获得最终的融合决策图.通过此步骤,可以使聚焦区域的判别更为精确,同时使聚焦区域的边缘过渡自然,有效地抑制融合图像中块效应和伪影现象的产生.将本文方法与现有的多种融合方法进行主观与客观实验对比,结果证明了本文方法的有效性.

2 鲁棒稀疏表示模型

鲁棒稀疏表示(RSR)可视为对SR模型的一种改进,该模型可以提高对非高斯噪声的鲁棒性.令Y=[y1,y2,…,yN]是一个大小为d×N的数据矩阵(即多聚焦图像),该数据矩阵的每一列yi∈Rd相当于一个数据向量(即一个图像块).假设该图像部分地被误差或噪声E∈Rd×N所污染,再给出一个拥有M个原子的字典D∈Rd×M,RSR模型可以由如下公式所定义:

(1)

其中,矩阵X∈RM×N代表所求的稀疏系数矩阵,‖X‖0代表矩阵X的l0范数,‖E‖2,0代表误差矩阵E的l2,0范数,D代表过完备字典,参数λ用来平衡上述两个分量在等式(1)中的影响.由文献[26]的研究可知,等式(1)所定义的RSR模型可以由如下优化问题来代替:

(2)

J=‖X‖1+λ‖E‖2,1+[L,Y-DX-E]+

(3)

其中,L是拉格朗日函数,用来消除公式(2)中的条件约束,μ>0是最后一项的惩罚参数,运算符[A,B]表示矩阵A和矩阵B的欧几里得内积.显然公式(3)现在是不受约束的,并且可以利用如下公式,通过固定X和E中的一项来求另一项的方法迭代循环计算该函数的最小值,直至收敛.计算公式如下:

(4)

(5)

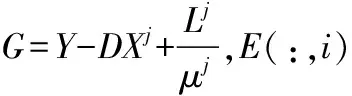
(6)

3 本文融合方法

本文基于RSR模型的融合框架可以分为如下四个步骤:

1)利用滑动窗口取块的方法,将源图像A和B分别分解成图像块序列.通过联合字典对图像块序列进行鲁棒稀疏表示,得到稀疏系数矩阵X和编码残差矩阵E;

2)分别对源图像A、B中相同位置处图像块序列的稀疏系数矩阵X和编码残差矩阵E的二范数加权求和,通过比较两者间的大小来得到初始的决策图;

3)通过对初始决策图进行形态学滤波和高斯滤波优化,得到融合使用的最终决策图;

4)根据得到的最终决策图对源图像A、B进行加权融合,得到最终的融合图像.上述融合步骤如图2所示.

3.1 联合字典的构建

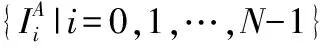
(7)

(8)

在多聚焦图像融合中,不同源图像的聚焦区域虽然不一致,但还是具有一定的相关性.仅使用单幅图像所构建出来的字典并不能得到最稀疏的系数,但是将不同源图像生成的字典联合成一个字典,就能使字典中的信息更加完备.因此,用联合后的字典再对源图像进行鲁棒稀疏表示,可以得到稀疏程度更高的稀疏系数.为此,本文构造了一种联合字典,将源图像IA和IB生成的两个字典联合成一个字典DAB,其中DAB=[DA,DB].再将DAB代回RSR模型中求解.

3.2 初始决策图的获得

传统的稀疏表示模型利用稀疏系数矩阵X作为判别聚焦区域的依据.而在RSR模型中,多聚焦图像被分解为一个非聚焦(或模糊)的部分,又称作重构后的矩阵DX,加上一个包含细节的部分,又称作重构误差矩阵E,如图1所示.换句话说,在RSR模型中,重构误差矩阵E包含了多聚焦图像中的高频细节信息.因此,传统的RSR方法以重构误差E来代替稀疏系数X对聚焦区域进行判别.

图1 lab图像的RSR分解示意图Fig.1 Illustration of RSR decomposition on lab

虽然DX代表着非聚焦部分,但事实上两幅聚焦区域不同的图像的DX并非完全相同,这说明DX中仍然包含着少许聚焦区域的信息.为此,本文将传统SR和RSR的方法相结合,在判别聚焦区域时,将DX也加入考虑,可以获得更加精确的聚焦区域.在本文中,取DX与E的加权二范数和作为比较的依据.详细的步骤如下:

1)利用联合字典DAB,通过如下算法1求解下列优化问题,以此得到数据矩阵YA、YB的鲁棒稀疏表示:

s.t.YA=DABXA+EA,diag(XA)=0

(9)

s.t.YB=DABXB+EB,diag(XB)=0

(10)

其中,XA、XB分别是源图像A、B的稀疏系数矩阵,EA、EB分别是源图像A、B的重构误差矩阵.约束条件diag(XA)=0与diag(XB)=0是为了避免EA、EB成为零矩阵[28].算法1如下:

算法1.通过LADMAP得到鲁棒稀疏表示模型算法

输入:数据矩阵Y,字典D,参数λ

输出:稀疏系数X,重构误差E

初始化:X0=0,E0=L0=0,ρ=1.1,ε=0.05,μ=10-6,μmax=1010

WHILE 结果未收敛 DO

1.固定X并利用公式(4)更新E;

2.固定E并利用公式(5)更新X;

3.利用如下公式更新拉格朗日函数L

Lj+1=Lj+μj(Y-DXj+1-Ej+1)

4.利用如下公式更新μ

μj+1=min(μjρ,μmax)

5.检查迭代条件是否成立

‖Y-DXj+1-Ej+1‖F/‖Y‖F<ε,

‖Xj+1-Xj‖∞<ε,‖Ej+1-Ej‖∞<ε

其中,‖.‖∞代表l∞范数,其含义为矩阵里每一行元素绝对值之和的最大值.

END WHILE

(11)

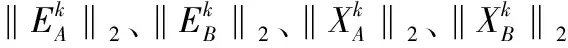
3.3 基于形态学滤波和高斯滤波的决策图优化

在获得初始决策图时,只是比较了单个图像块中的信息,而没有将邻近图像块内的信息加入考虑.这使得初始决策图中存在许多孤立的小块(或者称作“空穴”).这些“空穴”的存在说明部分聚焦区域未被正确地识别,或者部分非聚焦区域被误判成聚焦区域.在文献[25]中,通过引入了MRSR模型来解决该问题,但MRSR模型的计算复杂度比RSR模型高了许多,并且得到的融合决策图中仍存在许多“空穴”.为了减少“空穴”对图像融合的影响,同时降低计算的复杂度,本文通过两个步骤对初始决策图进行优化.首先,将决策图中孤立的小区域进行填充,填充过程如下:

M2=bwareaopen(M1,t)

(12)

式中,bwareaopen代表形态学滤波中的填充操作,代表滤波的阈值,M1为初始决策图.该填充操作可以将二值图像中少于t个像素的联通区域移除,得到一个没有“空穴”的新二值图像.形态学滤波的优化很好的消除了部分被误判的区域,有效抑制了融合图像中伪影的产生.在本文方法中,t值取10000可以得到最好的效果.

在使用二值图像作为多聚焦融合权重图时,由于聚焦与非聚焦区域的过渡不平滑,常常导致图像块效应在融合结果中出现.因此本文使用高斯滤波对形态学滤波填充过的决策图进行进一步优化,得到最终的融合权重图,即:

图2 本文的融合框架Fig.2 Schematic diagram of the proposed fusion frame

MF=M2*Gsr,σ

(13)

式(13)中,*代表卷积操作,Gsr,σ代表高斯滤波函数,r和σ分别为高斯滤波的参数,本文取r=7,σ=1.2.

3.4 融合源图像

获得最终的融合权重图后,对源图像进行加权得到最终的融合图像,即:

IF=MFIA+(1-MF)IB

(14)

式(14)中,IF为最终的融合图像.

4 实验结果及分析

为了验证本文所提出方法的有效性,本文选择了6组广泛应用于研究的多聚焦图像进行对比实验,包括lab、book、clock、flower、disk、paper.其中,lab、flower和disk大小均为320×240,book大小为400×300,clock大小为256×256,paper大小为322×234.如图3所示,除book外,其余图像均是未精确配准的,图3中第一排是聚焦于左侧的图像,第二排是对应的聚焦于右侧的图像.本文方法与七种当前主流的多聚焦图像融合方法进行了比较,包括图像抠图(IMF)[4]、引导滤波(GFF)[6]、多尺度权重梯度(MWGF)[7]、交叉双边滤波(CBF)[5]、自相似与深度信息(SSDI)[8]、NSCT结合稀疏表示(NSCT-SR)[21]和卷积神经网络(CNN)[18].本文对比实验中,七种方法的代码均是作者在其主页公布的,它们的参数选择均与各文献中保持一致,所有的实验均是在Matlab2014a上实现的,实验配置是3.20GHz的CPU和8GB的内存.

图3 六组多聚焦源图像Fig.3 Six groups of multi-focus source images

4.1 融合图像质量评价

融合图像的质量评价主要包括主观评价和客观评价两部分.由于融合技术地不断提升,主观评价的标准已经很难体现不同融合方法得到的效果的差异.在本文中,将同时考虑融合图像的主观视觉效果和客观定量评价,其中客观定量评价通过互信息(MI)[29]、边缘信息保持度(QAB/F)[30]和结构相似度(SSIM)[31]三种常用的图像融合质量评价标准来衡量.

4.2 融合的参数选择

由于公式(1)中提到的参数λ以及滑动取块时窗口大小px×py对融合结果有着重要的影响,我们需要找到可以使融合结果达到最优的参数.在本小节中,我们使用六幅图像的平均结果来测试不同参数对本文方法的影响.采用上一小节提到的三个质量评价指标来衡量不同参数得到的融合结果.

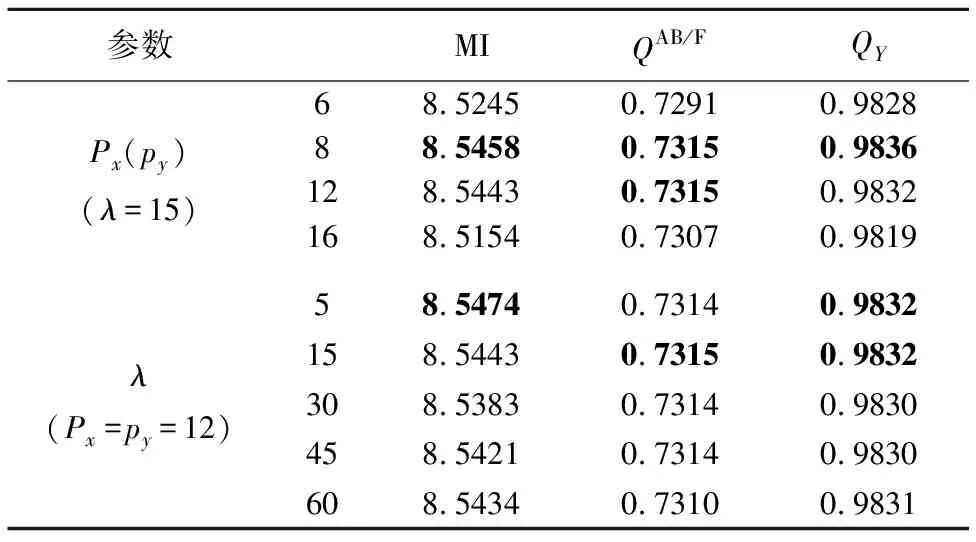
表1 不同参数下本文方法得到的融合结果Table 1 Fusion results obtained by different parameters

表1给出了不同参数下的融合结果.我们注意到,窗口尺寸px和py取8和12时,得到的结果相近,但是当px取12时计算复杂度大大降低,由表3可知,消耗时间只有px=8时的九分之一左右.因此综合考虑各个因素,本文窗口尺寸px和py取12.从表1中还可以看到,当λ取15时,可以得到最优的结果.因此在以下的实验中,取px=py=12,λ=15.

4.3 图像融合实验

4.3.1 主观视觉效果

图4给出了不同方法的lab融合结果.值得注意的是,由于拍摄时差,lab图中实验人员的头部相互具有明显的位移(如图3(a)),这说明两张源图像未完全配准.为了体现本文方法对未精确配准图像的鲁棒性,本文给出了融合图像与右聚焦源图像的归一化残差图.在残差图中,对应源图像聚焦区域的残差特征越少,则代表源图像聚焦区域所转移到融合图像中的信息越完整.相反,对于非聚焦区域则是应该具有更丰富的细节信息.为了得到更清晰的对比,本文对残差图进行了归一化处理:

(13)

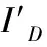
图4 不同方法的lab融合图像和对应残差图Fig.4 Fused images and their relevant residues of different fusion methods on lab

4.3.2 客观定量评价

为了进一步验证本文方法的性能,本文对七种方法的结果进行了客观质量评价.利用MI、QAB/F和QY对融合结果进行定量分析,评价结果如表2所示,其中粗体为所有方法中的最大值.从表2中可以直观地看出,本文方法的MI和QY的值均是最大,除了book之外QAB/F的值也均为最大,并且book的QAB/F值也与最大值相近.MI的值均为最大值,说明本文方法所获得的融合图像转移了更多来自源图像的原始信息.QY的值均为最大值,说明本文方法可以很好的保留源图像的结构信息.QAB/F的对比也说明本文方法总体上可以很好的保留源图像的边缘信息.因此,综合三个评价指标的表现来看,本文方法在有效信息提取上明显优于其他七种主流方法.

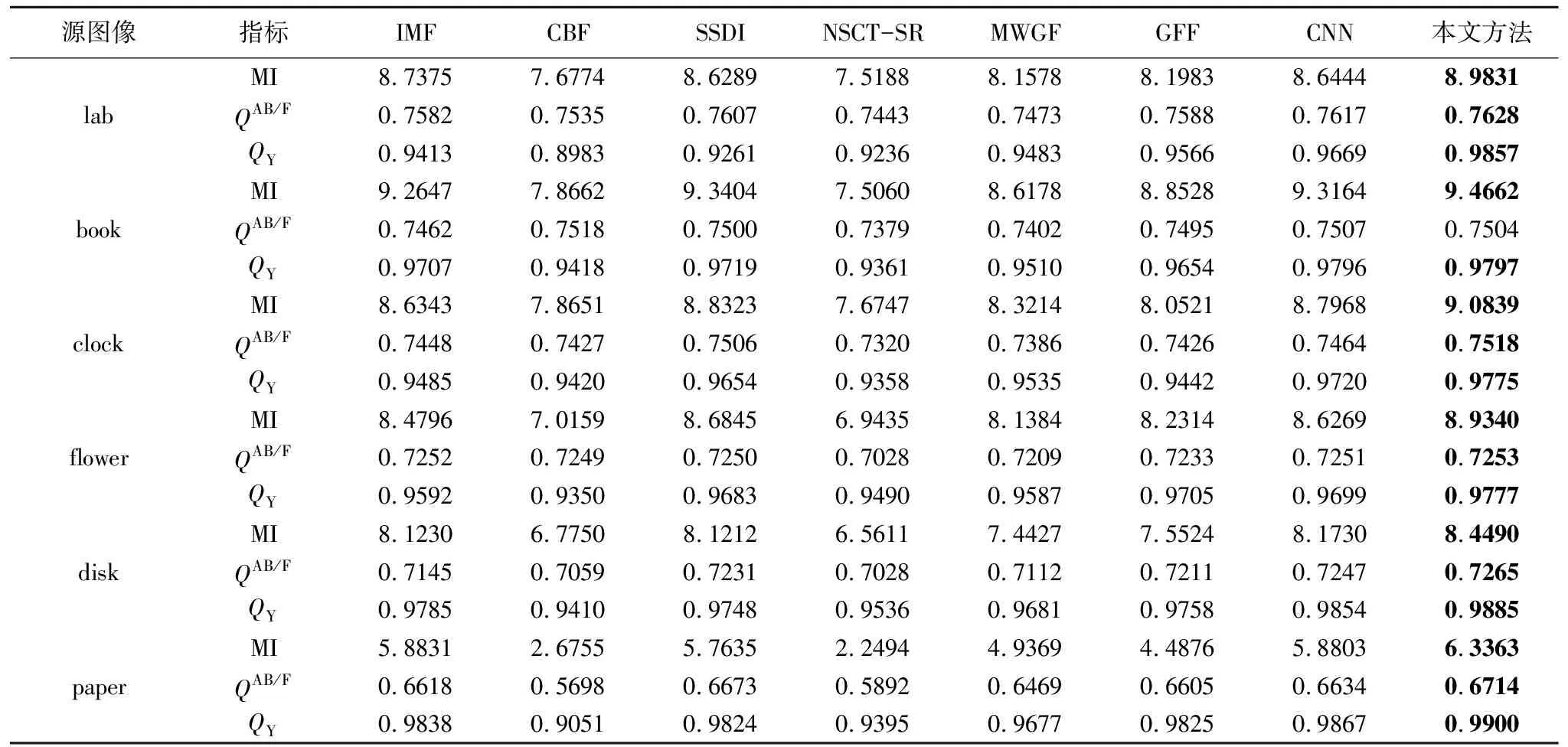
表2 不同融合方法得到的客观指标对比Table 2 Objective comparison of different multi-focus image fusion methods

4.3.3 关于联合字典与形态学滤波的对比试验

为了验证联合字典与形态学滤波在本文方法中的有效性,本节将未使用联合字典的鲁棒稀疏表示融合方法和未使用形态学滤波处理的鲁棒稀疏表示融合方法与本文方法进行了对比.对上述6组图进行融合的平均评价指标如表3所示.

表3 是否使用联合字典与形态学滤波的对比Table 3 Comparison of using the joint dictionary or morphological filtering

其中 MF-RSR代表使用形态学滤波处理但不使用联合字典的鲁棒稀疏表示融合方法,JD-RSR代表使用联合字典但不使用形态学滤波处理的鲁棒稀疏表示融合方法.由表3可以看出,MF-RSR与JD-RSR两种方法的MI、QAB/F与QY的值均低于本文方法.因此综合三个评价指标的表现来看,使用联合字典对图像进行鲁棒稀疏分解以及使用形态学滤波对决策图进行后处理可以有效提升融合图像的质量.

4.3.4 算法效率分析

表4给出了不同多聚焦图像融合方法在六组融合实验中的平均耗时.从表4中可以看出,GFF是目前效率最高的方法,可以做到实时性.IMF与MWGF是效率较高的两种方法,分别只需要2.82秒和1.65秒.CBF、SSDI与NSCT-SR的耗时均超过了10秒,效率相对较低.CNN是最耗时的方法,这是由于CNN使用了卷积神经网络,计算复杂度较高.但是CNN的融合效果与SSDI相近,并且优于其余方法.本文方法由于使用了RSR模型,计算复杂度略高于传统SR模型[25].但是本文方法在牺牲部分计算效率的基础上,得到的融合效果明显优于上述方法,并且计算耗时少于CNN.相信通过优化RSR模型的算法,可以进一步地提升计算效率,满足各种实际应用的要求.

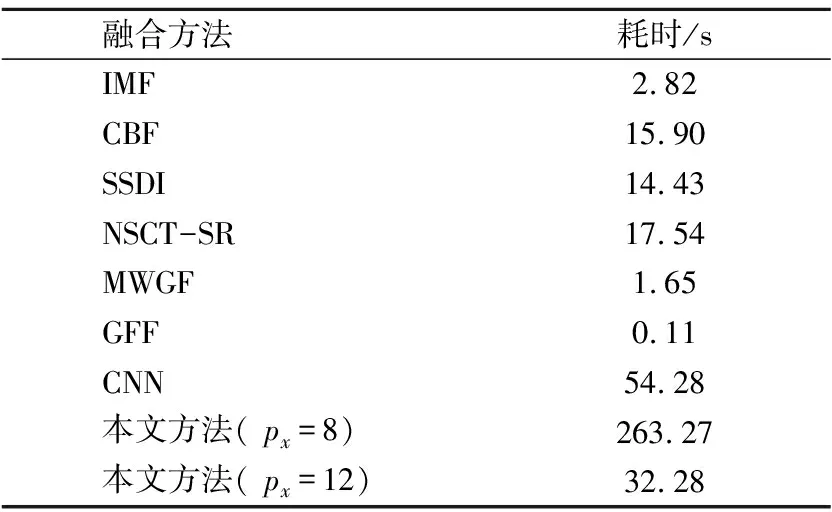
表4 不同融合方法的耗时对比Table 4 Comparison of time consuming in different fusion methods

5 结 论

本文提出一种基于鲁棒稀疏表示和形态学滤波的多聚焦图像融合方法.利用鲁棒稀疏表示模型对源图像进行处理,得到稀疏系数和重构误差,再求解两者的加权二范数和判别图像的聚焦区域,以此来获得初始的融合决策图.为了减少融合图像中伪影现象和块效应现象的产生,接着采用形态学滤波与高斯滤波对初始决策图进行优化,从而获得最终的融合决策图.最后,本文方法与七种主流的融合方法进行了对比实验,实验结果表明本文方法在视觉效果和定量指标上均优于其他方法.由于本文方法的计算效率并非最高,因此在下一步的工作中,将研究降低本文方法计算复杂度的优化算法.同时,还将考虑将本文方法应用在其他图像类型的融合技术上,如多模态医学图像融合和红外与可见光图像融合等.