基于等值负荷矩模型的辐射形配电网节点电压快速估算方法

刘禹良，郭剑峰

(重庆电力高等专科学校，重庆 400053)

当今社会，人们对电力能源的依赖性越来越强，对电能质量的要求也越来越高。配电网作为电力系统中直接针对用户的环节，对用户电能质量和供电可靠性有着直接的影响[1-2]。因此，合理选择配电网的接线方式和设备型号，正确配置网络中的继电保护、自动装置并整定其参数，具有十分重要的意义，而这一切工作均以正确、高效地计算配电网的潮流为基础。电力系统潮流计算的主要任务是确定网络中的功率分布及功率损耗，以及各节点的电压。实际电力系统的节点、支路数目繁多，且结构复杂，其潮流只能通过计算机进行迭代求解[3]，采用的算法主要有牛顿-拉夫逊法、PQ分解法等，这些迭代算法原理较为复杂，且均包含求解雅可比矩阵等消耗时间多、占用内存量大的中间过程[4]。

配电网常采用辐射形结构，接线方式包括放射式、干线式、链式3种基本类型，通常只有1个电源，通过电网向下游的多个负荷供电。其结构特点决定了任一负荷点只能从一个方向取得电能供应，且网络中任何一条支路的末端功率为下游所有负荷功率与下游所有支路的功率损耗之和。基于上述特征，辐射形配电网的潮流常采用“前推回代法”来进行，该算法实际上是由手算潮流方法改进而来，原理简单，其计算效率较前述迭代算法更高，耗费内存量却相对较小。但采用该方法求解潮流时也需要经历多轮迭代，且计及了功率损耗等一些次要因素，计算精度虽高但在耗费时间上并不能令人特别满意。因此，基于辐射形配电网的一些其他特征，提出了更加简化的潮流计算方法。

1 辐射形配电网潮流计算的简化

通常情况下，辐射形配电网，尤其是电压等级为35 kV及以下的地方网络，由于电压较低、线路较短(一般不超过50 km)、输送功率较小(最大传输有功一般不超过10 MW)，因此在潮流计算时可作如下简化[5]。

1)忽略电力网等值电路中的并联导纳支路

电力网等值电路主要由各线路和变压器的等值电路组成。这两类元件并联导纳中的功率损耗可近似认为与电压的平方成正比，由于地方电力网电压等级较低，并联导纳功率损耗的数值可忽略不计。

2)忽略串联阻抗中的功率损耗

电力网串联阻抗中的有功、无功损耗分别与电阻、电抗的大小成正比，也与流过线路和变压器的视在功率平方成正比。尽管地方电力网的串联阻抗不具备R≪X这一特征，但由于其网络规模小，其电阻、电抗值均较小，且输送容量小，因此串联阻抗中的功率损耗可忽略不计。

基于上述两点，则配电网中任一元件的功率损耗均忽略不计，其首端和末端的功率相等，这可使潮流计算过程得到简化。

3)忽略电压降落的横分量

由电力系统潮流计算的知识可知，对于110 kV及以下的电力网，可忽略电压降落横分量，近似认为电压损耗等于电压降落纵分量的大小。例如，分别以U1，U2表示某支路(线路或变压器)首、末端的电压大小(归算至同一电压等级下的值)，则有

U2=U1-ΔU

(1)

式中，ΔU为线路的电压损耗，若忽略电压降落横分量，可近似认为

(2)

式中：P，Q分别为线路(或变压器)串联支路首端(或末端)的有功、无功功率：R,X分别为支路电阻和电抗；U为首端(或末端)的电压。

忽略电压降落横分量后，网络中各节点电压仅有大小上的差别，而没有相角之差，这使得潮流计算得到进一步简化。事实上，地方电力网各支路首末两端的电压相角差很小，通常都在允许的范围之内。

4)用线路额定电压代替各点实际电压计算电压损耗

由于地方电力网靠近用户，其各节点的电压质量关系到用户的电压质量，因此要求其采取各种措施，保证其各节点电压质量合格。基于此，各节点电压大小都在额定电压附近。为简化计算工作，可用线路额定电压代替各点实际电压计算电压损耗，这样式(2)可改写为

(3)

若采用标幺值计算方法，则各节点电压大小为1 p.u.，式(3)可改写为

ΔU=PR+QX

(4)

2 基于等值负荷矩模型的地方辐射形配电网潮流快速估算方法

定义：支路i～j上有功功率、电阻的乘积与无功功率、电抗的乘积之和为该支路的等值负荷矩，记为tij，有

tij=PijRij+QijXij

(5)

式中，Pij，Qij，Rij，Xij分别为支路i～j的有功功率、无功功率、电阻、电抗。

式(4)、(5)说明，采用第2节中提出的辐射形配电网潮流计算的简化措施后，某支路的等值负荷矩约等于该支路的电压损耗，即

tij=ΔUij

(6)

由辐射形配电网结构及其潮流分布的特点可知，在忽略功率损耗的情况下，任一支路i～j流过的复功率为该线路所有下游负荷点的复功率总和，即

(7)

式中，m为该线路下游负荷点的总个数。

联立式(5)、(7)，有

(8)

式(8)即为支路i～j等值负荷矩的计算公式。

在忽略各节点电压相位差的情况下，网络中任意两节点i，j间的电压差等于从节点i到节点j所经各支路的电压损耗之和，即

(9)

式中：l为从节点i到j所经支路的数目；ΔUk为第k条支路上的电压降。

根据前述分析，可近似认为配电网中任意两节点i，j间的电压差约为从节点i到节点j所经各支路的等值负荷矩之和，即

(10)

式中，tk为第k条支路的等值负荷矩。

定义：节点i到节点j所经各支路的等值负荷矩之和为节点j相对于节点i的等值负荷矩，记为Tij，即

(11)

式(10)、(11)构成估算任意两节点i，j间电压差的等值负荷矩模型。

若节点i的电压Ui已知，则Uj的估计值为

Uj=Ui-Tij

(12)

利用该模型估算各节点电压存在一定误差，主要原因有以下两点。

其一，该模型忽略了各支路的功率损耗，使各支路电压损耗的估算值偏小。

其二，应用式(4)估算支路电压损耗时，认为首节点的电压约等于1 p.u.，而实际中许多节点电压的真实值并不刚好等于1 p.u.，会造成电压损耗的估算值偏大或偏小。通常，越靠近末端负荷的节点，其电压越低，常常低于1 p.u.，这样会使与这些节点相关联的支路电压损耗估算值比真实值偏小，从而造成这些节点电压的估算值比真实值偏大。

为解决上述问题，将所有节点电压平均估计值Uaver的倒数作为修正因子，乘以用式(5)计算出的各支路电压损耗(或等值负荷矩)估算值，得到各支路电压损耗的修正值，即

(13)

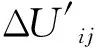
若节点i的电压已修正，则可计算节点j电压的修正值为

(14)

根据各支路电压损耗的修正值，重新估算各节点电压，可大大提高估算精度。

综合上述分析，可得出配电网各节点电压估算流程：

1)初始化首端节点(平衡节点)电压值(通常取1 p.u.)；

2)从各末端节点(负荷点)出发，逐步向首端节点前推，估算各支路的功率及等值负荷矩；

3)从首端节点出发，逐步向各末端节点回推，利用式(12)计算各节点电压的估算值；

4)将所有节点电压估算值的平均值的倒数作为修正因子，利用式(13)计算各支路电压损耗的修正值；

5)再次从首端节点出发，逐步向各末端节点回推，利用式(14)计算各节点电压的修正值。

从上述估算流程可见，与计及支路功率损耗的多轮迭代的前推回代法相比，利用本文算法仅需经历一次前推、回推的过程即可实现各支路电压损耗的快速估算，且由于忽略了各支路功率损耗，进一步缩短了计算时间。本文算法的计算误差将在第3节通过算例进行验证。

3 算例分析

应用IEEE 33节点配电网[6](其网络拓扑结构见图1，电气参数详见表1)，对第2节介绍的节点电压估算方法进行验证。

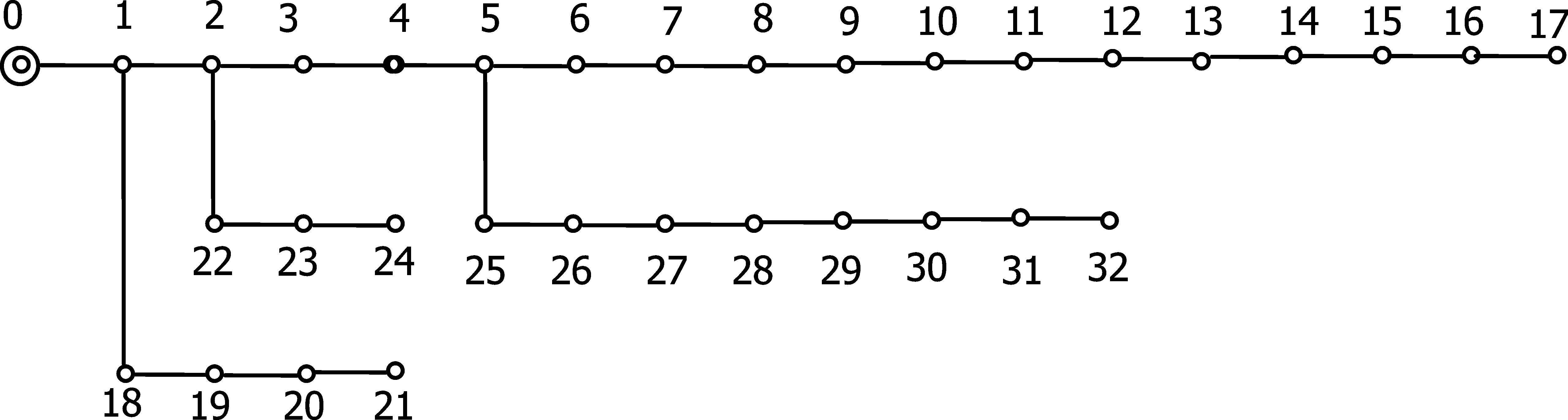
图1 IEEE 33节点配电网

支路号首、末端母线阻抗/Ω负荷/kVA支路号首、末端母线阻抗/Ω负荷/kVA10-10.092 2+j0.047 0100+j601716-170.164 0+j0.156 590+j4021-20.493 0+j0.251 190+j401817-181.504 2+j1.355 490+j4032-30.366 0+j0.186 4120+j801918-190.409 5+j0.478 490+j4043-40.381 1+j0.194 160+j302019-200.708 9+j0.937 390+j4054-50.819 0+j0.707 060+j202120-210.451 2+j0.308 390+j4065-60.187 2+j0.618 8200+j1002221-220.898 0+j0.709 190+j5076-70.711 4+j0.235 1200+j1002322-230.896 0+j0.701 190+j5087-81.030 0+j0.740 060+j202423-240.203 0+j0.103 4420+j20098-91.044 0+j0.740 060+j202524-250.284 2+j0.144 760+j25109-100.196 6+j0.065 045+j302625-261.059 0+j0.933 760+j251110-110.374 4+j0.123 860+j352726-270.804 2+j0.700 660+j201211-121.468 0+j1.155 060+j352827-280.507 5+j0.258 5120+j701312-130.541 6+j0.712 9120+j802928-290.974 4+j0.963 0200+j6001413-140.591 0+j0.526 060+j103029-300.310 5+j0.361 9150+j701514-150.746 3+j0.545 060+j203130-310.341 0+j0.530 2210+j1001615-161.289 0+j1.721 060+j203231-320.164 0+j0.156 560+j40

采用MATLAB R2009a编制潮流程序，分别用第2节介绍的估算方法和前推回代法计算各节点电压标幺值，将两种方法的计算结果一并列入表2中(为简化起见，只列出了部分节点电压值)。

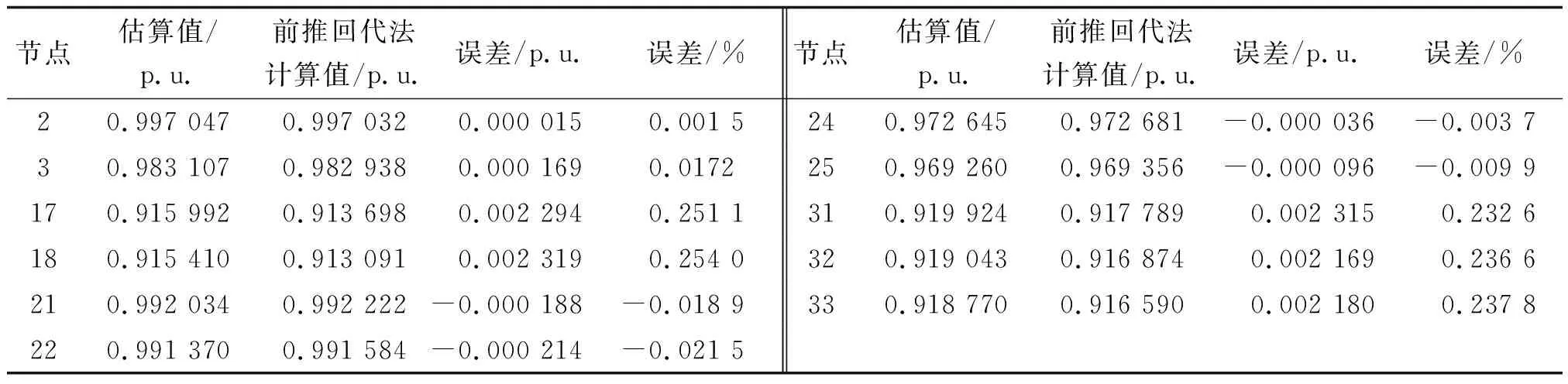
表2 IEEE 33节点配电网部分节点电压计算结果(收敛精度1.0×e-5)

注：取三相功率基准值SB=10 MVA，线电压基准值UB=12.66 kV，平衡节点电压设为1.0 p.u.

表2的计算结果表明，应用本文第2节中提出的算法，得到的各节点电压估算值与前推回代法的精确计算结果相比，误差很小。比较结果证实，本文节点电压估算的等值负荷矩模型能满足工程上的精度要求。

就计算速度来看，应用前推回代法计算精确潮流耗时0.002 808 s，而应用本文估算法仅耗时0.000 791 s，不到前者的1/3。事实上，应用前推回代法计算该网络潮流共经历了3次迭代过程，对于节点数目较多的复杂配电网，其迭代次数更多，若利用本文算法进行潮流估算，速度优势更加明显。

4 结论

本文提出基于等值负荷矩模型的辐射形配电网节点电压快速估算方法。该算法根据辐射形配电网的结构、参数、潮流分布特征，给出等值负荷矩定义，并用等值负荷矩代替支路电压损耗，且仅用一轮前推、回代的过程即可实现各支路电压损耗的快速估算，从而实现各节点电压的初步估算；再将各节点电压初步估算值的平均数的倒数作为修正因子，对各支路电压损耗进行修正，从而得到各节点电压的最终估算结果。利用MATLAB R2009a编程对IEEE 33节点配电网进行潮流计算，将本文算法与前推回代法的计算结果和耗时进行对比，证明了本文算法的正确性和高效性。