基于峰度系数的行人水平行走步态细化分类算法
鲍 深, 张金艺,, 姚维强, 梁 滨
(1.上海大学微电子研究与开发中心,上海200444;2.上海大学特种光纤与光接入网省部共建重点实验室,上海200444)
在现代生活中,各种便携式个人导航设备已经成为人们日常生活中不可或缺的一部分.因此,基于位置的服务(location based service,LBS)[1]也变得越来越受欢迎.基于微机电系统(micro-electro-mechanical system,MEMS)[2]惯性传感器的行人航位推算(pedestrian dead reckoning,PDR)[3]定位导航技术,不需要任何基础设施便可获得行人位置,因此成为当今研究的热点之一.该技术的实现难点之一是对行走距离的估计,包括步频检测和步长估计[4]两方面.因为行人运动时的步态变化非常复杂,若是算法精度不高,随着定位时间的推移,定位结果会有较大的误差[5].因此,国内外很多科研工作者致力于研究如何进行行人步态分类,以期得到精确的个人航迹推算.
目前,基于MEMS惯性传感器技术的行人步态分类方法大都是基于加速度峰值[6-7]判断当前行人的步态类型.由于布朗运动造成的仪器自有噪声及环境等因素的干扰,该方法采集到的加速度信号带有许多伪峰值,从而降低了最终分类结果的精度.针对这一问题,Lan等[8]根据行人走路的步频采用通频带为0.625∼20.000 Hz的带通滤波器对采集到的原始数据进行滤波,但最终的分类结果并不令人满意.卢先领等[9]使用8种时频特征参数训练基于支持向量机的多类步态分类器,虽然该方法精度较高,但因特征参数过多导致识别过程过于复杂.Clements等[10]提出了一种融合时域、频域两类特征的步态分类方法,对走和跑两种步态模式进行实验区分,但是该方法为剔除伪峰值添加了峰值阈值、两峰间隔等限定条件,需要对样本进行大量分析,从而造成工作量较大且分类精度不高的问题.
为减少伪峰值对最终分类结果的影响,本工作从整体波形角度出发,通过分析行人前进时的加速度波形,将加速度信号的峰度系数[11-12]设定为特征参数,取代传统方法中使用的加速度峰-峰值.为进一步减小误差,除去信号中的伪峰值,首先使用快速傅里叶变换将加速度信号从时域转换到频域,并对获得的频域信号模值取平方;然后通过傅立叶逆变换回到时域,得到原信号的自放大信号;最后,计算出自放大信号的峰度系数,并通过分析峰度系数值,对行人的水平行走步态进行细化分类.验证结果表明,本工作提出的细化分类算法的精度达到了98.62%,与加速度值-频率功率融合算法相比,对步态的分类更为细化,同时分类精度提高了7.37%.
1 步态特征参数选择
一般情况下,行人走路的步频为1∼3 Hz.为了实现水平行走的步态细化分类,将行人走路分为3种步态:慢走、走和慢跑.由于这3种步态在时域上的表现较为相似,为了准确区分,需要设定合适的特征参数.
行人水平行走时的步频越大,前进方向上的加速度值也越大,其波形也越陡峭.根据这一特性,本工作选取峰度系数作为步态特征参数.峰度系数是描述变量所有取值分布形态陡缓程度的统计量,反映了曲线顶端的扁平程度.峰度系数K为

图1是某受试者分别以慢走、走和慢跑3种步态行走时的加速度信号时域图,其中Z轴方向上的加速度值为aZ,单位为g,g表示重力加速度.Z轴方向即水平前进方向,在3轴中选取Z轴作为研究对象的原因是其对于水平行走的分类识别影响最大,而受个体影响又小于另两轴.图1反映了行人以不同步频行走时时加速度信号波形的特点.由图1可以看出:行人行走越快,加速度信号的波形曲线会变得越陡峭,峰度系数值就越大.
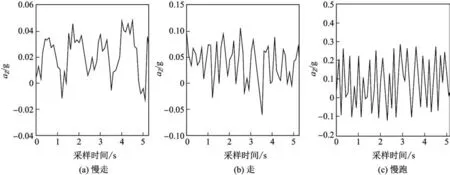
图1 行人以不同步态行走时的加速度信号Fig.1 Acceleration signals of pedestrian level walking with different gait
2 自放大信号提取
由于仪器自有噪声及环境等因素干扰,采集到的信号会存在许多伪峰值,直接计算加速度信号的峰度系数会产生较大的误差,因此剔除信号中的伪峰值至关重要.本工作以快速傅里叶变换作为工具对步态加速度信号aZ(t)进行预处理,计算出aZ(t)的自放大信号AZ(t),替代aZ(t)作为步态信号.

式中,F表示快速傅里叶变换,F−1表示快速傅里叶逆变换.假设采集到的加速度信号为
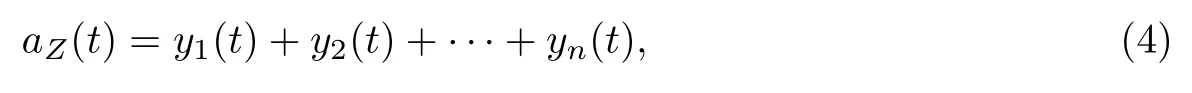
对aZ(t)进行快速傅里叶变换.假设采样点数为N,那么得到N个复数,每一个复数代表一个频率点.除第一个点表示直流分量(即0 Hz)外,每个点都可以用复数a+bi表示.设第m个点代表真正的加速度信号,其模为Am=(a×a+b×b)0.5,相位θm=arctan(b/a).由Am和θm可以计算出对应的信号表达式
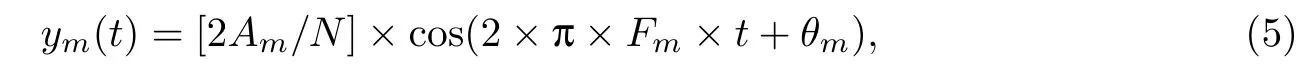
式中,m/=1且m≤N/2,Fm为该点对应的频率.
除ym(t)外,其他的加速度信号均为噪声信号.为了除去噪声信号,需要先将频域中信号的模值进行平方因为真正的步态加速度信号的模值Am比噪声的模值大好几个数量级,将模值平方后,这种差距会进一步拉大.因此,与A2m相比,噪声模值的平方值几乎可以忽略不计.最后,对进行快速傅里叶逆变换,得到自放大信号AZ(t),
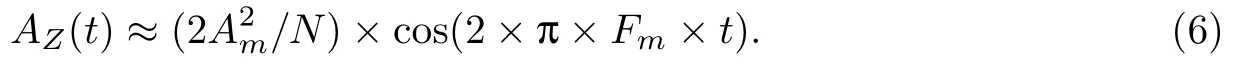
由式(6)可知,自放大信号AZ(t)约等于真正的步态加速度信号的模值Am平方后的值.
图2和3是行人慢走时的加速度信号aZ(t)和自放大信号AZ(t)的时域图.从图中可以明显看出,aZ(t)中存在的伪峰值在AZ(t)中基本消失,这表明对aZ(t)的预处理是成功的.另外,aZ(t)和AZ(t)的波峰并没有出现在同一时刻,这是因为最后是对|X(f)|2进行快速傅里叶逆变换,而|X(f)|2是一个实数,虚部为0,相位由arctan(b/a)变为0.
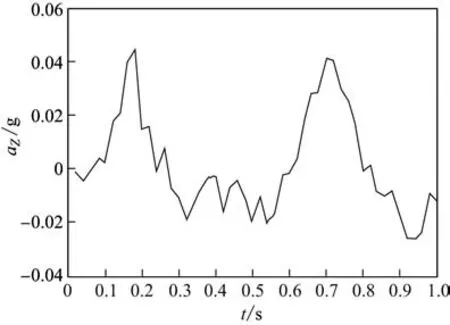
图2 行人慢走时加速度信号Fig.2 Acceleration signals of pedestrians jogging

图3 行人慢走时自放大信号Fig.3 Self-amplif i ed signal of pedestrians jogging
3 步态细化
本工作将自放大信号AZ(t)的峰度系数K作为特征参数,因此进行步态分类时需计算出AZ(t)和对应的K值.
步骤1 将前进方向上的加速度信号记作aZ(t),实时提取行走过程中的aZ(t).
步骤2 通过窗口分割对步态信号进行加窗,对采集到的加速度信号aZ(t)进行分段处理.为保证窗口内至少有一步完整的步态加速度数据,且提高分类的实时性,所用的窗口宽度为50个采样点,是传感器1 s内所采集的数据量.
步骤3 对一个窗口内的步态数据进行计算,求出自相关信号AZ(t)及其峰度系数K.
步骤4 一个窗口的计算结束后,采用滑动窗口法,移动半个窗口,即25个采样点,重复步骤3.
按上述步骤进行多次实验后,可以得出不同步态所对应的K值范围.根据当前步态的K值,能够识别当前的步态类型.
图4为基于峰度系数的行人水平行走步态细化分类流程.由图4可以看出,首先计算出当前窗口中加速度信号aZ(t)的自放大信号AZ(t)的峰度系数K,然后通过实验得出的对应关系判断当前步态Lc.考虑到传感器的精度问题,Lc还要与前两次步态Lp1,Lp2进行对比,通过步态的连续性完成最终的分类.

图4 行人水平行进的步态细化分类流程图Fig.4 Flowchart of gait detailed classif i cation of pedestrian level walking
由图4可知,本工作只需先后计算出加速度信号aZ(t)的自放大信号AZ(t)及其峰度系数K的值,然后根据K的值就能初步判断当前步态Lc.在完成最终的分类时,本方法仅需考虑上两次步态Lp1,Lp2与本次步态Lc的连续性.而传统的峰值判别法较复杂,不仅需要对原始步态波形进行滤波,在最终判断时还需要添加各种限定条件,如对波峰波谷值进行阈值判断、对两个波峰间设定时间间隔等.因此,相比较而言,本工作提出的判断方法简单,计算量小.
4 验证系统及结果分析
4.1 验证系统

图5 SDK MPU91开发板Fig.5 SDKMPU915 development board
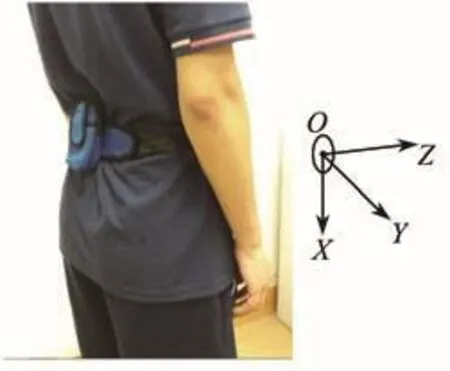
图6 人体坐标系Fig.6 Coordinates of body
进行验证时,MSP430单片机首先将步态数据读出,接着蓝牙模块以115 200 bits/s的波特率将数据传输给计算机,再由计算机进行数据的计算及最后的步态分类.MSP430单片机的采样频率为50 Hz.根据采样定理可知,采样频率要求大于信号频率的2倍,因此可检测的信号频带为0∼25 Hz,涵盖了行人行走时的步频.
4.2 结果分析
为了能够采集到具有普遍性和稳定性的数据样本,选取5男5女共10名不同身高体重的健康受试者.采集时受试者都穿运动鞋,并采用舒适正常的步行方式,在一段长约50 m的走廊上(见图7)来回行走.每位受试者分别以慢走、走、慢跑3种步态进行水平行走,重复20次.
对实验结果进行分析,得出峰度系数和步态的对应关系,如表1所示.从表中可知:当自放大信号AZ(t)的峰度系数为1.0∼4.5时,此时行人的步态类型为慢走;当峰度系数为4.5∼10.0时,步态类型为走;当峰度系数为10.0∼24.0时,步态类型为慢跑.即当行人步行速度越快时,自放大信号AZ(t)的峰度系数越大,这与本工作最初的预想是一致的.

图7 实验场所Fig.7 Experiment place

表1 行人水平的走步态和峰度系数的对应关系Table 1 Correlation between kurtosis and gait of pedestriam level walking
文献[10]中的算法融合了时域和频域两类特征,在时域上为加速度信号设置了阈值,频域上则采用了频率功率,而分类结果也只包括走和慢跑两种.滤波法是计算滤波后加速度信号aZ的峰度系数,然后根据峰度系数的值进行分类.将根据本工作中提出的方法得到的分类结果与文献[10]中的方法以及滤波法得到的分类结果进行对比,结果如表2所示.由表2可知:本工作提出的基于峰度系数的步态细化算法,由于在信号预处理时对加速度信号aZ进行了放大,得到了自放大信号AZ(t),这与对加速度信号aZ直接进行滤波相比,不同步态的峰度系数的阈值更加明显,识别率达到了98.62%;相较于传统的时频域融合算法提高了7.37%,且在行人水平行走时对步态的分类更为细化.

表2 行人水平行走步态分类方法实验结果的对比Table 2 Comparison of with the experimental results of gait classif i cation algorithms of pedestriam level walking %
5 结束语
传统的行人步态分类方法通常是将加速度峰-峰值作为特征参数,但由于最终的分类结果会受到由布朗运动造成的仪器自有噪声及环境等因素的干扰,从而出现分类结果错误,最终导致分类精度下降,针对这一问题,本工作创新性地提出了一种基于峰度系数的行人水平行走步态细化分类算法,该算法使用峰度系数K作为特征参数,只需根据K值就能判断出与其对应的步态完成分类,减少了算法的复杂度.此外,使用自放大信号AZ(t)取代传统的滤波方法中对加速度信号aZ进行预处理,使得峰度系数的阈值更加明显,提高了分类精度.实验数据证明了基于峰度系数的行人水平行走步态细化分类算法对慢走、走和跑的区分效果要优于传统的时频域融合算法.因此,对该步态的化分其法进行改进,利用该算法对其他多种人体步态进行识别是下一步的研究工作.

