基于优化组合核最小二乘支持向量机的脉动风速预测

基于数据驱动技术的样本学习和训练为信号预测提供一个可行的途径.信号预测的方法主要有时间序列、神经网络、支持向量机(support rector machine,SVM)等[1-5],但这些方法在理论或应用上都存在不足.例如:时间序列方法中的高阶模型参数估计难度大,而低阶模型预测精度低.传统的人工神经网络存在运行时间长、容易陷入局部极小等问题.SVM通过核函数定义的非线性变换将输入空间变换到高维空间,并在这个高维空间中寻找输入变量和输出变量的线性关系,解决了“维数灾难”问题,然而核函数的选择和参数优化决定了SVM的特性.

本工作利用Hilbert空间运算的封闭性,首先将B(包括B1、B3和B5)样条核函数和径向基(radial basic function,RBF)核函数进行线性组合,构造B-RBF组合核函数,进而提出基于粒子群优化(particle swarm optimization,PSO)B-RBF核的最小二乘支持向量机(least squares support vector machine,LSSVM).最后使用某超高层建筑的脉动风速样本数据数值验证PSO-B-RBF-LSSVM的预测性能.

1 最小二乘支持向量机

式中,ω为权向量,b为偏置项,C为惩罚参数,ei∈R为误差,e∈Rl×l为误差向量.为解决式(1)的优化问题,构造Lagrange函数:

对式(2)求偏导,并根据最优化理论中的KKT(Karush-Kuhn-Tucher)条件,可以得到如下等式和约束条件:

式中,i=1,2,···,l. 设α =(α1,α2,···,αl)T,Q=(1,1,···,1)T,Y=(y1,y2,···,yl)T,I 为单位矩阵.联立求解方程组,消去ω和ei,则式(3)的解为

最后,得到LSSVM的回归模型为

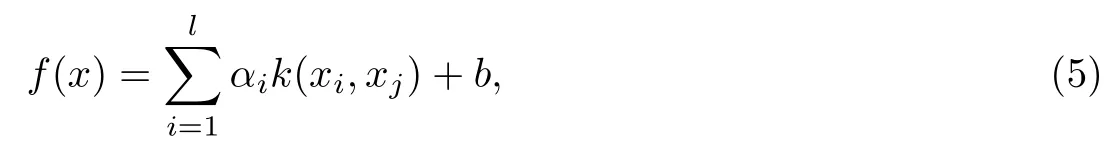
2 B-RBF组合核函数

给定训练集X=(x1,x2,···,xp)和核函数k(x,x′),定义核内元素k(xu,xv),u,v=1,2,···,p的矩阵为核矩阵或Gram矩阵.对于所有的训练集X,如果它的核矩阵是对称且半正定的,则函数K为有效核.

RBF核函数为

式中,σ为核宽度.因此,它的核矩阵为

RBF核函数的核矩阵K(xu,xv)具有如下性质:

B样条核函数为

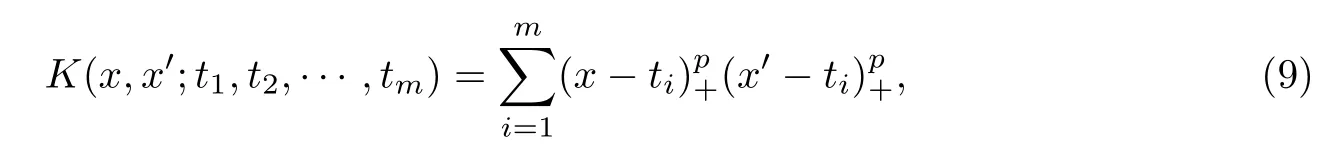
因此,它的核矩阵为

B样条核函数的核矩阵K(xu,xv)具有如下性质:

因此,组合核函数核矩阵为

式中,α为加权系数,σ为核宽度.组合核函数的核矩阵K(xu,xv)具有如下性质:

3 PSO-B-RBF-LSSVM模型

3.1 模型参数

B-RBF组合核函数的参数分别为惩罚参数C、核参数σ(核宽度)、核参数p(次数)和权重α.采用粒子群优化(particle swarm optimization,PSO)算法对于上述参数进行优化,建立基于PSO-B-RBF核的LSSVM.

(1)进行粒子种群初始化.设定粒子群维数为4,种群规模m=50,最大迭代次数K=100,以及初始速度矩阵以及初始粒子个体最优位置和全局最优位置.

(2)RBF核函数待优化参数分别取c∈[0,1 000]和σ2∈[0.01,100.00].

(3)定义粒子适应度F(xi)为均方根误差函数,并将F(xi)与自身最优适应度Fp和全局最优适应度Fg进行比较,据此调整粒子个体最优位置和全局最优位置.粒子适应度函数为

式中,yi为第i个样本的实测值,fi为第i个样本的预测值.

(4)更新粒子的速度和位置,获得新的PSO-B-RBF核LSSVM参数.

(5)当迭代次数达到最大迭代次数K或适应度的值满足要求时,停止迭代,得到优化参数,建立PSO-B-RBF-LSSVM模型.

PSO-B-RBF-LSSVM的流程如图1所示.

图1 PSO-B-RBF-LSSVM流程Fig.1 Flow chart of PSO-B-RBF-LSSVM

3.2 数值验证

采用自回归滑动平均(auto-regressive and moving arerage,ARMA)模型对某超高层建筑高200 m的脉动风速进行模拟.由地面开始每间隔10 m设置一个风速模拟点,选择60和130 m高度处的脉动风速时程作为样本,用于学习训练和验证预测算法.脉动风速时程如图2所示.

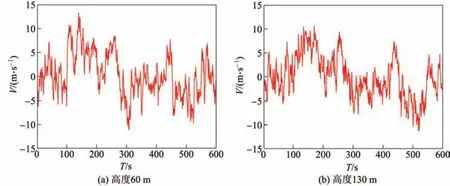
图2 脉动风速时程样本Fig.2 Simulation of f l uctuating wind speed time-history series

(1)分别将60和130 m处的模拟风速时程前500 s(500个采样点)的数据作为训练集,后100 s(100个采样点)的数据作为测试集.取嵌入维数k=10,运用交叉验证法对样本数据进行相关空间重构.首先,将风速时程样本进行归一化处理后输入到B-RBF组合核函数中,构造核函数矩阵;然后,采用PSO方法选取各项参数值,建立PSO-B-RBF-LSSVM的预测回归模型;最后,对后100 s采样时间点的脉动风速进行预测.分别计算60和130 m处风速时程样本中的前500 s采样时间点(训练集)和预测结果中的100 s采样时间点(测试集)的脉动风速与实际(模拟)风速样本数据的相关系数R、平均绝对误差(mean absolute error,MAE)及均方根误差(root mean squoore error,RMSE),对PSO-B-RBF-LSSVM预测性能进行评价.数值计算结果分别如图3∼4和表1∼2所示.

图3 60 m处预测风速与实际风速的比较Fig.3 Comparison of forecast wind speed and actual wind speed at 60 m

由表1和2可以发现,B样条核LSSVM的预测结果好于PSO-RBF核LSSVM,这是因为RBF的局部性特征明显,只能对小范围内的样本数据产生影响,而B样条函数核的全局性较好,具有很强的外推能力.根据Mercer核定理,利用RBF的局部性和B样条函数核的全局性特点,线性相加(αRBF+(1−α)B样条函数核)构造出的B-RBF组合核函数兼顾了局部性和全局性特征.因此,B-RBF-LSSVM能进一步提高脉动风速的预测性能.值得指出的是,在B1,B3和B5样条函数核中,B3样条函数核在计算精度和速度方面表现均衡,是更为理想的一种核函数.因此,PSO-B3-RBF-LSSVM比PSO-B1-RBF-LSSVM,PSO-B5-RBF-LSSVM和PSO-RBF-LSSVM具有更好的预测性能.

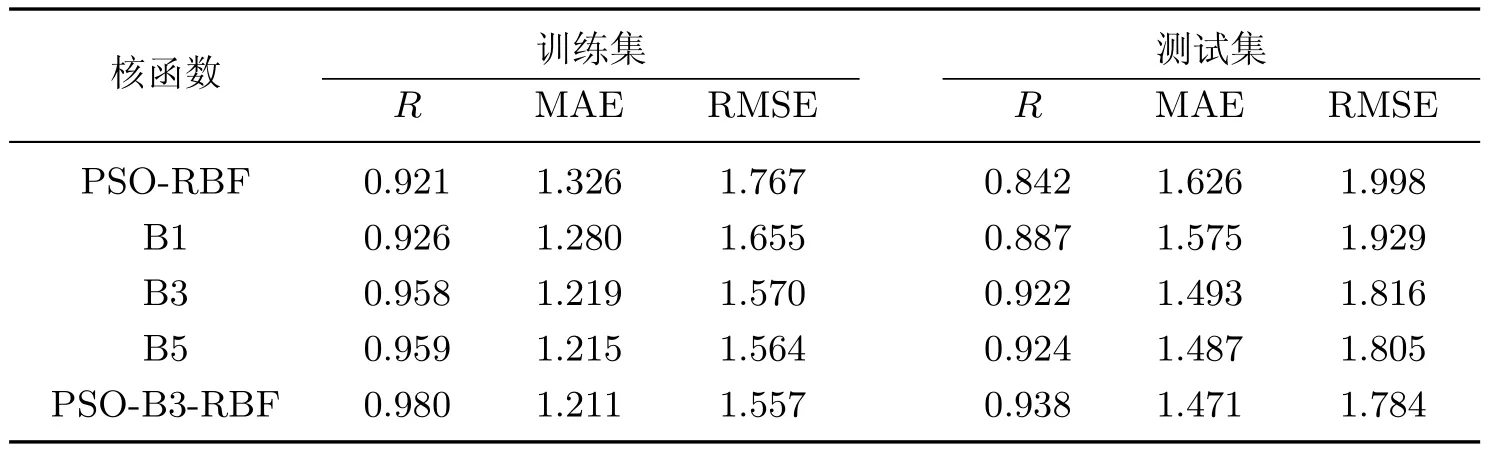
表1 60 m处脉动风速的预测性能指标Table 1 Prediction performance index of f l uctuating wind velocity at 60 m

表2 130 m处脉动风速的预测性能指标Table 2 Prediction performance index of f l uctuating wind velocity at 130 m

4 结束语

本工作首先将B样条(B1,B3和B5)核函数和径向基核函数进行线性组合构造了BRBF组合核函数,然后建立了基于PSO-B-RBF的最小二乘支持向量机,最后使用某超高层建筑的脉动风速模拟样本数据验证了模型的预测性能.数值结果分析表明,PSO-B3-RBFLSSVM比PSO-B1-RBF-LSSVM,PSO-B5-RBF-LSSVM和PSO-RBF-LSSVM具有更好的预测性能.