考虑救援点资源分布的救援车辆路径优化

韩亚娟,杨宇航,彭运芳

(上海大学管理学院,上海200444)

应急物资调度是应急保障体系中的重要一环.当大规模突发事件爆发后,应急物资必须在尽可能短的时间内运达各受灾点.近年来,国内外对应急物资调度问题的研究逐渐深入,并取得了较为丰富的研究成果.Wang等[1]研究了确定需求下应急物流的开放式车辆路径问题.Ceselli等[2]研究了药品配送中的选址和车辆路径问题.Wohlgemuth等[3]研究了确定需求条件下应急救援车辆动态路径问题.Lei等[4]对随机需求环境下的车辆路径问题进行了研究.上述研究多建立在车辆物资足够多的情况下,较少地考虑资源有限性.程碧荣等[5]针对救援期内物资供应可能不足的特点,考虑随机需求并建立了应急救援车辆路径模型.石彪等[6]针对大规模突发事件爆发后应急物资运输车辆不足的情况,建立了两阶段应急物资配送模型,有效提升了应急物资运输车辆的使用效率.马祖军等[7]和代颖等[8-9]综合考虑应急物资需求的模糊性、限制期和多次往返配送,研究了一类多目标开放式定位路径问题.另外,刘长石等[10]以应急物资运达时间最短和总成本最优为目标函数,构建了多目标模糊优化模型,重点考虑了受灾点的情况.廖成等[11]设计了一种多模式分层网络,并利用延期费用和划分时段的方法构建了应急物资车辆路径的多目标数学规划模型.何正文等[12]考虑了交通网络的道路和节点带有禁止时间窗的情况,以减少应急物资的调运时间为目标构建了整数规划模型.基于上述分析可知,目前对于应急救援车辆路径优化的研究,多是直接定位于受灾点的具体情况,而较少考虑救援点的特殊情形.如果灾害发生初期物资总量有限,且各个救援点的物资量与车辆运输能力比值有显著差别,那么某些救援点的物资输出效率则会成为瓶颈,无法使总体救援时间最短.因此,本工作考虑在救援系统中构建一个物资集散区以协调救援系统内各个救援点的资源,从而达到优化救援效率的目的.

1 问题描述

重大灾害爆发后,需在尽可能短的时间内将应急物资配送到各个受灾点.本工作假设有多个地理位置已知的受灾点和救援点,这些救援点的物资总量略多于受灾点物资总需求量,且救援点的物资量与车辆运输能力比值不平衡,各个救援点的救援车辆无权限前往其他救援点.在上述特定情形下,本工作考虑在救援系统内部构建一个物资集散区来平衡各个救援点的物资量与车辆运输能力.基于此,救援车辆分为两类:第一类车辆负责将物资从救援点运达物资集散区,第二类车辆直接参与救援,若救援物资不足,则救援车辆从物资集散区处获取物资以完成剩余任务.决策问题是确定每个救援车辆的路径,使所有受灾点都得到救援的时间最短.

第一类车辆把物资从救援点运往物资集散区,每次载运物资量为车辆容量.若到达救援点时救援过程未完成且救援点物资量不足,则该类车辆载运量为其所属救援点的剩余物资量.第二类车辆在初始阶段满载离开救援点并直接参与受灾点的救援,其路径规则如下:开始阶段车辆从其所属救援点出发到达救援任务的第一个受灾点,然后按照救援顺序继续救援下一个受灾点;若到达某受灾点时无法满足该受灾点物资需求,则车辆从该受灾点出发到物资集散区获取物资并原路返回继续救援.第二类救援车辆每次从物资集散区获取的物资量规则如下:若救援车辆非最后一次去物资集散区,则获取物资量为车辆容量;若救援车辆最后一次去物资集散区,则该次从物资集散区获取的物资量只需满足救援任务中后续受灾点的物资需求即可.救援车辆在物资集散区的排队规则如下:先到车辆的物资需求量必须被满足的情况下,后到车辆才能获取物资.另外为便于建立模型,假设任意两辆车不会同时到达物资集散区.

基于上述路径规则,本工作中救援车辆的路径模式如图1表示.假设存在3个受灾点和2个救援点,其中救援点S1拥有车辆1和车辆2,救援点S2拥有车辆3和车辆4.救援点S1的车辆2去物资集散区B1,而车辆1先到受灾点P1,再到受灾点P2.在到达受灾点P2时发现物资不足,则前往物资集散区B1获取物资并原路返回.救援点S2的车辆3去物资集散区B1,而车辆4先到受灾点P3,发现物资不足,接着去物资集散区B1获取物资并原路返回.在本例中,救援点S1的车辆1和救援点S2的车辆4属于第二类车辆,而救援点S1的车辆2和救援点S2的车辆3属于第一类车辆.

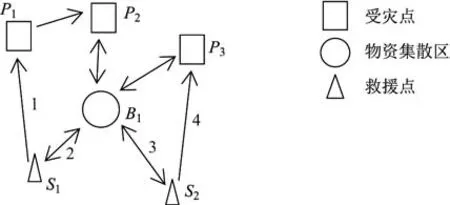
图1 救援车辆的路径模式Fig.1 Path pattern of rescue vehicle

2 数学模型

2.1 参数与变量

为便于描述,定义如下参数:V为车辆集合,v为救援车辆,vmax为车辆总数,D为受灾点集合,d为受灾点,S为救援点集合,s为救援点;td为受灾点d到物资集散区的时间,ts为救援点s到物资集散区的时间,tsd为救援点s到受灾点d的时间,td′d为受灾点到受灾点d的时间;rs为救援点s的物资拥有量,rd为受灾点d的物资需求量,rv为车辆v的容量;

定义V1为直接参与救援的车辆集合,vn为车辆v救助受灾点的个数,dvi为车辆v第i次救助的受灾点,cvi为救援车辆v第i次对受灾点救援时需要去物资集散区的次数;为救援车辆v第i次对受灾点救援时第c次到达物资集散区的时间;为救援车辆v第i次对受灾点救援时第c次离开物资集散区的时间,为救援车辆v第i次对受灾点救援时第c次需要从物资集散区获取的物资量,lvi为救援车辆v从第i次救援的受灾点离开时所携带的剩余物资量;fs(x)为救援点s到达物资集散区的物资量函数;

决策变量如下:

2.2 函数定义

为便于建立模型,定义两个函数.

定义1 若函数f(x)满足对任意的x1＜x2,有f(x1)≤f(x2),则定义函数

函数y的含义为:若存在a使得f(a)≥θ,且对于任意满足f(b)≥θ的b都有a≤b,则y=a.

定义2 假设任何两辆车不会同时到达物资集散区,故以每辆车每次到达物资集散区的时间为自变量,以该车该次需要从物资集散区获取的物资量为因变量,构造函数

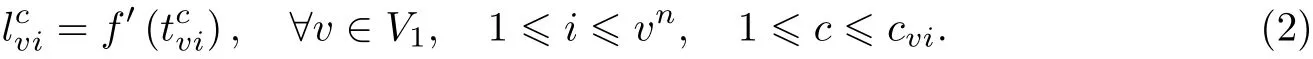
由函数(2),可根据每辆车每次到达物资集散区的时间对应得出该车该次需要从物资集散区获取的物资量.

2.3 模型构建

所有受灾点都得到救援的时间一共包含4部分.

(1)救援车辆从起始救援点出发到第一个受灾点的时间

(2)受灾点之间的运输时间

(3)从受灾点到物资集散区的往返时间

(4)救援车辆在物资集散区的等待时间)

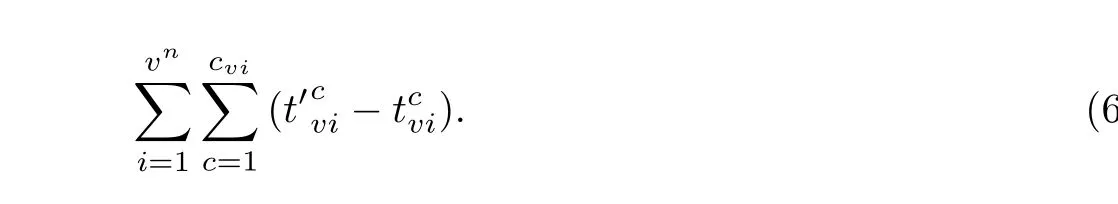
总的目标函数和约束条件如下:

式(7)表示模型的优化目标为救援时间最短.式(8)和(9)表示同一辆车只能参与一个任务.式(10)表示一个受灾点只能被一辆车救援.式(11)表示车辆的路径分配必须使救援点能够满足受灾点的物资需求.式(12)表示所有车辆在救援第一个受灾点时需要去物资集散区的次数约束.式(13)表示所有车辆在救援非第一个受灾点时需要去物资集散区的次数约束.式(14)表示救援车辆每次从物资集散区获取的物资量约束.式(15)表示救援车辆到达物资集散区的时间约束.式(16)表示救援车辆离开物资集散区的时间约束.式(17)表示救援车辆从受灾点离开时所携带的剩余物资量约束.

3 模拟退火算法设计

本工作采用模拟退火算法[13-16]求解车辆的救援路径.基于文献[17],本工作设计了一种解的表示方法.假设受灾点有M个,首先设置M个位点,每个位点与每个受灾点对应.每个位点由两个数字表示,第一个数字代表服务于该受灾点的车辆,第二个数字代表该车辆第几步服务于该点.结果会构造长度为2M的解,该解遵循两个原则:①该解不能包含所有车辆,因为必须有部分车辆服务于物资集散区;②若某车辆在初始解中出现过N次,则从1到N的N个整数必须分别出现在该车辆对应位点的第二个数字中.例如,编号分别为1,2,3,4的4个受灾点需要救援,那么32222131代表的是3号车辆路径为4-1,2号车辆路径为3-2.

3.1 解的评价

求解组合优化问题,需要对解进行相关评价,使算法在迭代过程中不断搜索到质量更优的解.本工作中解的表示方式隐含能够满足一个受灾点只接受一个车辆的救援,但无法满足受灾点的物资需求量约束.假设受灾点的总物资需求量为某条不可行路径中救援点一共可以提供的物资量为若则该解为可行解;若则该解为不可行解.设该不可行解的目标函数值为Z,且对每条不可行路径的惩罚权重为Pλ,则该解的评价值为

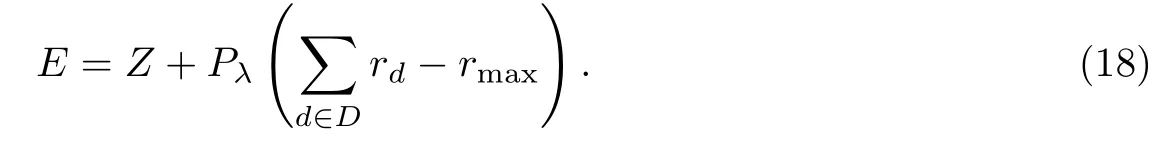
3.2 邻域操作

采用随机替换的方法进行邻域操作,具体操作过程如下.

步骤1 在总车辆集合V中随机挑选一辆救援车辆v1,在当前解所包含车辆集合中随机抽取一辆救援车辆v2,判断v1=v2是否成立.是,重复此步骤;否则,转步骤2.

步骤3 找出v2最后一次服务的受灾点,把该受灾点的车辆替换为v1,转步骤4.

步骤4判断v1在该受灾点的服务次序.若则其次序为1;若且v1在中最大的服务次序为,则在新解中v1在该受灾点的服务次序为

上述步骤1是为避免产生相同解,步骤2保证至少有部分车辆为物资集散区提供物资.

3.3 实现过程

模拟退火算法的具体实现过程如下.

步骤1 按照解的表示方式构造算法初始解.

步骤2 按照上述邻域操作方法的步骤进行.

步骤3 采用固定比率方式降温,即tk+1=a·tk,其中a为降温系数.

步骤4 采用固定的迭代步长,步长根据问题的规模确定.

步骤5 在温度下降指定次数后终止运算.

3.4 算法分析

模拟退火算法设计了较为直观的解结构,能够间接要求两种救援任务必须都有车辆参与,有效分配相关任务给对应车辆,以应对救援系统中的救援点资源分布不平衡情况.在邻域操作步骤中,迭代过程能够保持解的结构不变,且该过程可在时间复杂度不超过O(n2)的情形下完成运算.

4 算例

4.1 仿真数据

为简化运算,依据基本规则生成一个具有11个受灾点(P1∼P11)、2个救援点(S1,S2)和2个候选物资集散区(B1,B2)的救援网络.A车型容量为9.0 t,B车型容量为7.2 t,C车型容量为6.3 t.救援点S1的A车型车辆编号分别为1,2,3,B车型车辆编号分别为4,5,C车型车辆编号为6.救援点S2的A车型车辆编号为7,C车型车辆编号分别为8,9.救援点的物资总量为111 t,受灾点的物资需求总量为99 t,可认为救援点物资总量略多于受灾点物资需求总量.本实例其他相关数据如表1和表2所示.

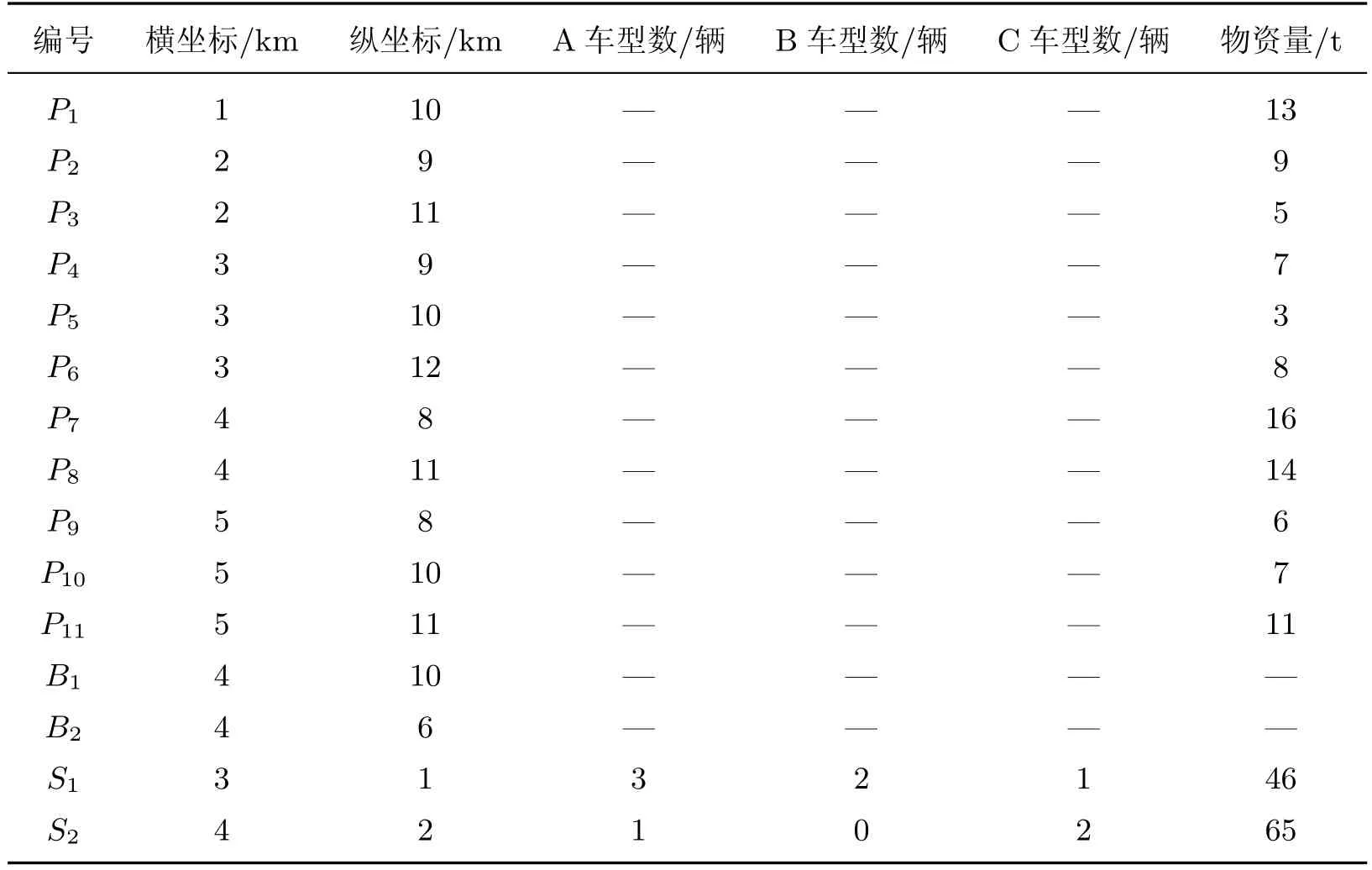
表1 初始点坐标及相关数据Table 1 Coordinates of each point and other related data

4.2 平衡性评价指标

将救援点的物资量与车辆运输能力比值作为该救援点的资源平衡性评价指标,有

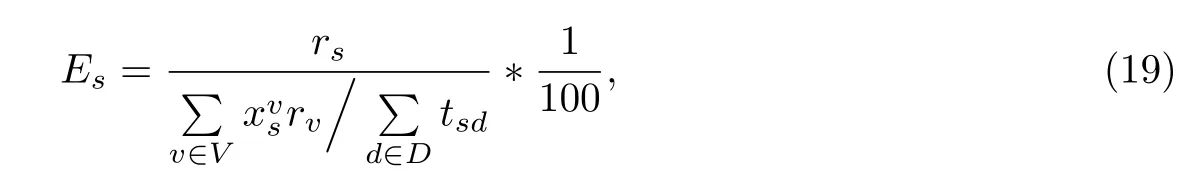
式中,rs为该救援点的物资所有量,为该救援点的车辆容量之和为该救援点到所有受灾点的时间之和.

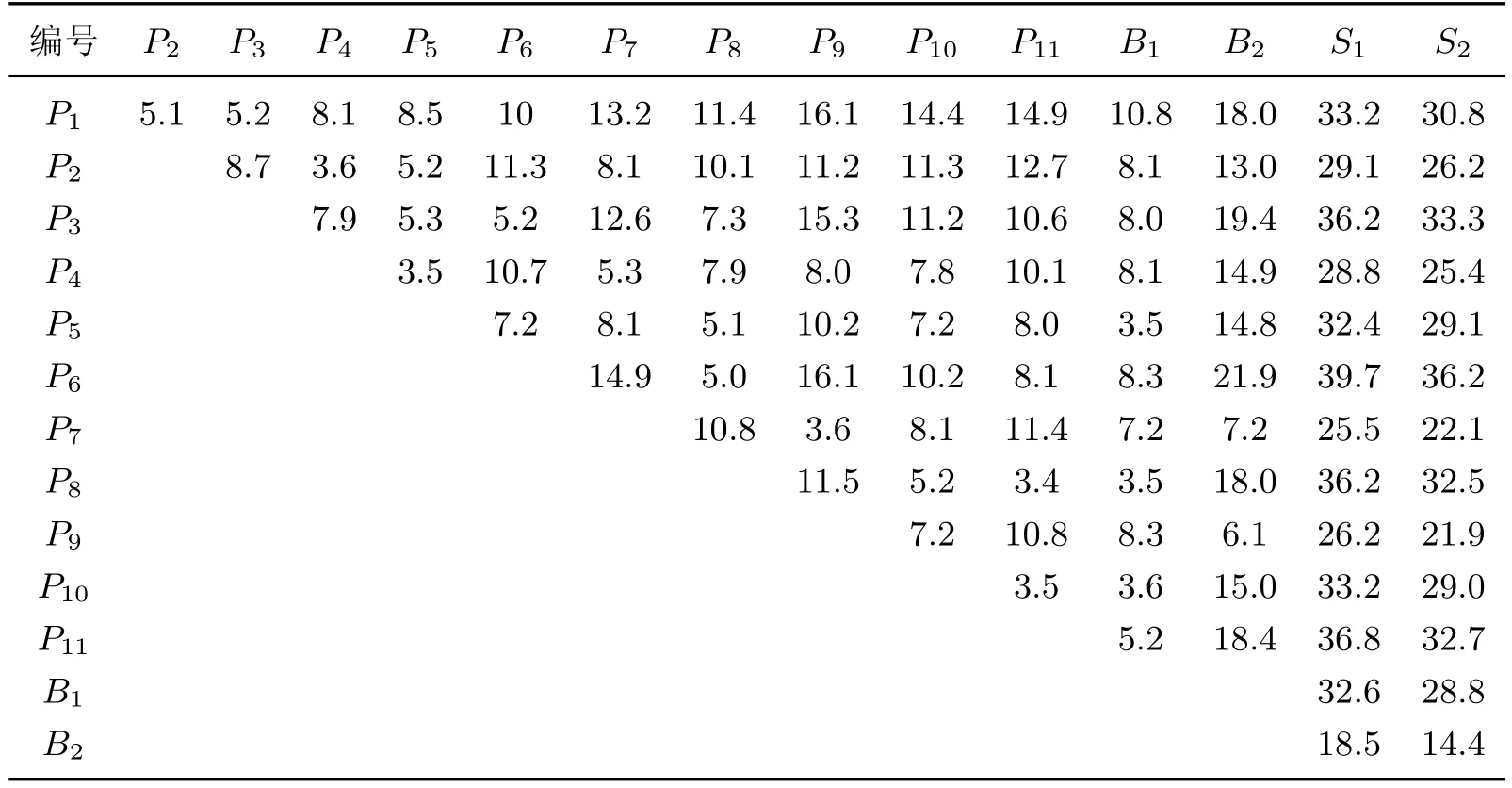
表2 各点间的行程时间Table 2 Travel time between points min

为判断两个救援点S1与S2的资源分布平衡性差异,定义指标

4.3 运行结果

本工作取初始温度260°C,降温速率0.98,降温次数200,每个温度迭代80次.使用JAVA编程,随机运行20次,两个物资集散区对应的最优解如表3和表4所示.

表 3 B1最优解Table 3 Optimum solution of B1

表 4 B2最优解Table 4 Optimum solution of B2

由表3和表4可知，在最优解对应的车辆路径中,救援点S1中的车辆多作为第二类车辆参与受灾点的救援,而救援点S2中的车辆多作为第一类车辆把救援点的物资运往物资集散区.该算例表明,基于物资集散区的车辆路径优化方法适用于救援点资源分布不平衡的情况.通过物资集散区的协调,一些物资量相对较大的救援点可以将物资配送到物资集散区,供第一类车辆使用;而车辆运输能力强的救援点可以将其车辆作为第一类车辆使用.另外,物资集散区B1和物资集散区B2对应的最优解分别为154.8 min和126.0 min,说明选择地理位置较好的物资集散区会改善救援效果.

5 结束语

在考虑物资集散区的基础上,本工作将所有救援点车辆分为两类:一类负责把物资从救援点运到物资集散区,另一类参与受灾点的救援.研究结果表明,本工作提出的车辆路径优化方法适用于资源分布不平衡的情形,能够改善救援的效率.但是,在各个救援点的物资量与其车辆运输能力相对平衡时,基于物资集散区的车辆路径优化方法效果不显著.

本工作仅考虑了单个物资集散区.当存在多个物资集散区时,部分救援点分需求的物资集散区如何分配才能达到最优救援效率,是下一步的研究内容.另外,本工作中的排序规则仅考虑了救援车辆到达时间,并没有考虑救援车辆获取的物资量大小和其他具体因素,如何更改救援车辆在物资集散区的排序规则来改善救援效率也是需要进一步研究的.