顾及多源神经网络的复杂网络异常识别

王建国

(阳泉师范高等专科学校 信息技术系，山西 阳泉 045200)

随着网络信息技术的快速发展，网络异常识别得到了日益广泛的应用[1]，通过在源程序中添加自主识别功能可以使得该设计可追踪性变强[2-3]。为了能够在复杂网络中实现对这些网络的有效识别，要求能够对复杂网络关系的本质进行准确的判别[4]。但是，依靠神经网络进行复杂网络异常的识别是十分复杂的[5]，传统的设计网络识别工作多数都是通过分析网络结构来实现的[6]，而对于复杂网络环境的考虑并不周全[7]。

针对当前研究中存在的不足，本文提出利用多源神经网络进行复杂网络异常识别。通过对备忘录网络中的实例进行研究，详细地描述识别流程。在对网络结构进行研究时，形态分析属于较为常见的分析方法，主要是对网络进行分析。本文依据网络特征来进行归类，使得具有相同网络特征的能够归为一类，得到一个抽象个体，以此将网络结构通过有限抽象个体进行描述。本文利用形态分析技术，就网络结构是否具有某种异常特征进行识别。为了实现这一目标，对当前已有的三值逻辑结构进行扩充，对具有网络特征的结构进行有效识别，随后结合网络形态结构及其变化方式设计识别网络异常的方法。最后，借助Stuttgart Neural Network Simulator(SNNS)模拟器就本文方法的有效性进行展示和验证。

1 多源神经网络异常识别过程

利用这种三值逻辑结构对网络成员之间存在的引用结构进行表示与说明。其中,U代表论域，其主要组成成分为个体individual，而且还可将个体进行具体划分，得到确定个体与不确定个体两类。确定个体与运行对象是具有一一对应关系，不确定个体，则对应的运行对象不止一个。在确保网络不被遗漏的基础上，对该结构进行严格识别。P(网络P)代表的是能够对论域个体间具有的引用关系进行合理描述，ι代表的则是在将P中网络表达式在各个体上应用之后对应的取值，在该结构中利用的逻辑结构为Cleane，对于确定值用0或者1来进行表示，而如果不是确定真值，则是利用1/2来进行表达。一般情况下，对于具体的三值逻辑结构利用符号σ来表示，或者可将其称之为异常网络。而且还可将异常网络以一种更加直观的方式进行表达，也就是形态图。在该图中，各节点与个体之间是具有对应关系的,而且是以实线对应表示普通的节点，而对于缩略节点则是以虚线来表示，并且这些虚线与实线反映了在个体中存在的各种确定与不确定性关系。假如个体u能够被变量x所直接引用，那么此时将会存在一条线是由x指向u的。如图1所示的四种异常网络，在σ(s1)结构中，u1和u2代表的是确定个体，各自都与一个对象相对应，其中的u2代表的是不确定个体，与之相对应的对象超过一个。

对于三值逻辑结构而言，可以将其中的网络进行细分，得到辅助网络以及核心网络等，网络之间的差异可以作为对复杂网络异常识别的依据。核心网络(core predicate)代表的是在对象引用方面程序设计语言所具有的网络，具体来讲，对于图1中的σ(s1)结构，是满足条件x(u1)=1,p(u1,u2)=1/2,p(u2,u2)=1/2的，此时,他能够反映出u1代表的对象确定被x引用，而p对u2所代表的对象应用是否存在是无法确定的。而且还可借助p使得u2所代表的对象之间发生反应或者相互作用。此外，辅助网络(instrument ation predicate)是基于核心网络进行的界定，能够反映特定分析对应的网络信息。而基于前两种网络能够界定宏网络(macro predicate)，该网络的设置主要是为了更加方便地进行表述，因此不需要对其进行设置。此外，还可以基于自由变量数量进行网络设置，得到一元以及多元网络，其中前者主要就个体属性进行描述，而后者主要是对个体之间存在的引用关系进行描述,而且在全部的一元网络中，将具有相同取值的对象经过合并后得到一个缩略个体。

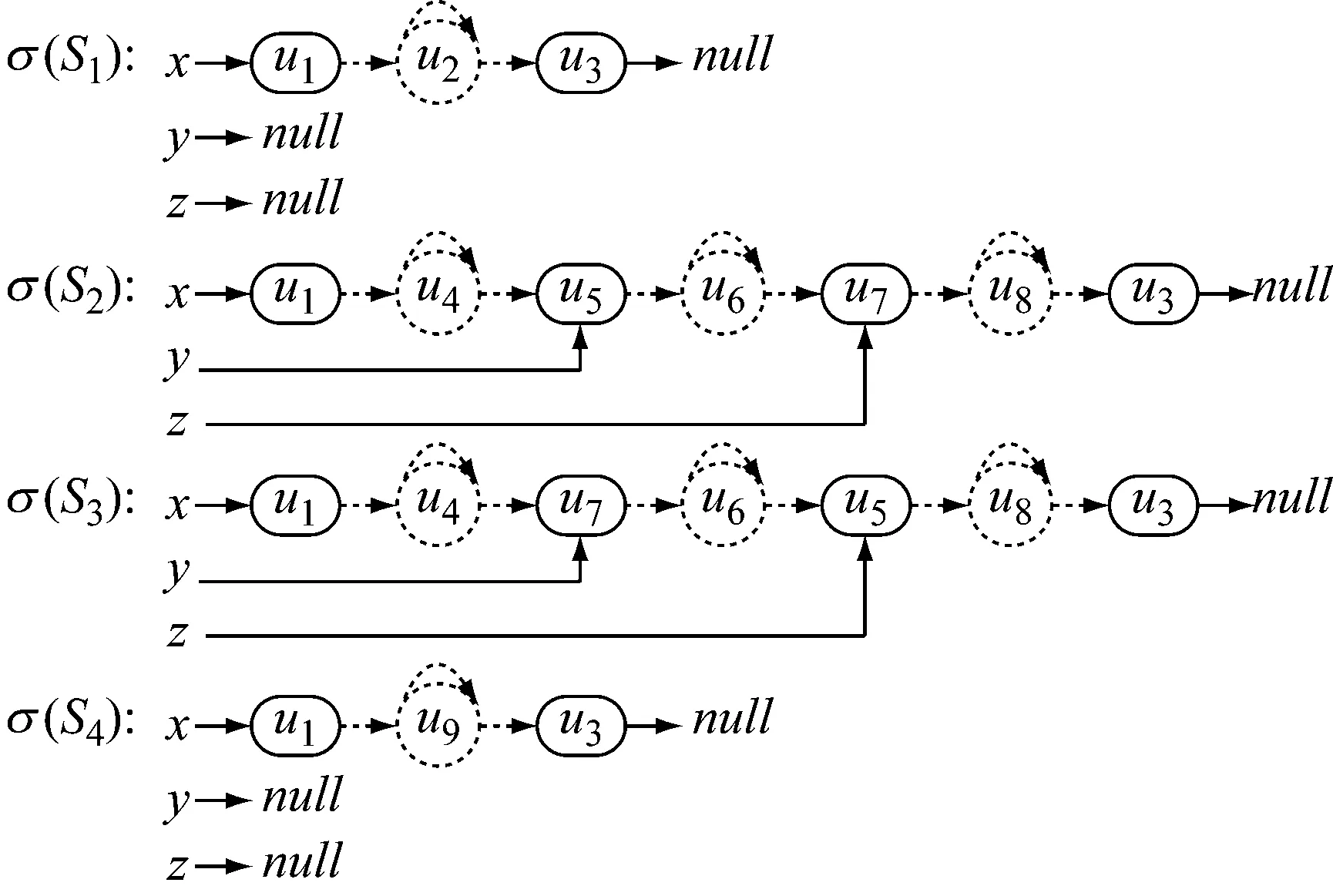
图1 互换两个对象位置的操作

如果正在执行程序中的某些语句，那么将使得网络结构产生改变。所以，如果要对形态进行详细研究时，需要调用一些基本赋值，找到网络相对应的时变函数，然后，需要对整个控制流程图从头到尾进行搜索，同时参照相应的程序进行初始化设置和查询实变函数，只有这样,才能够更加准确地找到每个子程序相应的异常网络。伴随着结构的改变，许多模糊的单个网络也将会改变，最终可以获得相应的个体。因为一元网络的取值相同，这些个体还可能被顾及，进而得到新的个体。为了能够对不同结构中同一对象具有的可追踪性进行分析，在文章中还提出了分化网络FocusTo(s1,s2,s3)、合并网络MergeTo(s1,u1,s2,u2)和流入网络InFlow(s1,u1,s2,u2)作为表达不同结构中对象间的可达关系。本文设计了网络R[p](s1,u1,s2,u2),并将上述四种网络都归入到结构间网络中,其中的辅助网络分为分化与合并两种，其余两种则为宏网络。其中的变元中的s1、s2与程序控制流图的节点是对应的，表示了在执行语句前后，程序所具有的状态，将其以4表示，而且如果是在状态σ(s)下，对应的φ的取值为φ@σ(s)。

以具有对象可追踪性特征的网络为例,对追踪过程进行阐述。

(1) 假如在控制流图上有两个点s1，s2，s1∈prev+(s2)(表示在控制流图中，s1是s2的直接或间接前驱)，σ(s1)中的个体u被分化为σ(s2)中的个体{u1,u2,…,un}，则FocusTo(s1,u,s2,ui)=1，其中，1≤i≤n。

(2) 如果有控制流图上的两个点s1，s2，s1∈prev+(s2)，σ(s1)中的个体{u1,u2,…,un}在σ(s2)中被合并为个体u，则MergeTo(s1,ui,s2,u)=1，其中，1≤i≤n。

图1所示的是对象位置交换的实现过程，其中的s1～s4代表的是在执行过程中，对应的程序点，σ(s1)-σ(s4)代表的则是与之相对的异常网络，σ(s1)中的u2在σ(s2)中被分化成u4～u8这5个个体,在σ(s3)中，u5和u7交换位置。在σ(s4)中，u4～u8这5个个体由于在x(u)，y(u)和z(u)这3个一元网络上的取值均为0，因此被合并为不确定个体在此过程中，有

FocusTo(s1,u2,s2,ui)=1,

MergeTo(s3,ui,s4,u9)=1

其中，4≤i≤8。

FocusTo和MergeTo关系可以通过分化操作以及合并操作获得。就如何得到异常网络变迁进行了方法上的阐述。在进行网络公式推导的阶段，就会执行分化程序，在后期改变的清除阶段，将会对以上操作实施。FocusTo和MergeTo显然满足传递性，即

FocusTo(s1,u1,s2,u2)∧FocusTo(s2,u2,

s3,u3)⟹FocusTo(s1,u1,s3,u3)

MergeTo(s1,u1,s2,u2)∧MergeTo(s2,u2,

s3,u3)⟹MergeTo(s1,u1,s3,u3)

为了进一步使各过程中个体具有更强的可追踪性，在本文中还进行了如下界定：

InFlow(s1,u1,s2,u2)⟺FocusTo(s1,u1,s2,u2)∨

MergeTo(s1,u1,s2,u2)

综合上述分析能够得出，InFlow关系是具有可传递性的。还应当明确的是，这种InFlow关系和FlowTo关系不是一样的，是存在区别的，在后者中主要是对两个栈变量关联网络交集问题进行描述。

2 实例分析

本文主要就如何在开源程序SNNS中实现对复杂网络异常的有效识别进行了说明，所使用的LER内大约有1 000个节点，节点的平均度数值为20，其中，最大的节点度数高达50，节点度数分布采用-2的幂指数函数，除此之外，参数一般取值为0.3，最终组成一个数据库，此数据库仅仅有一个节点数度数最大可以为20。文章首先可以对网络异常结构从网络角度进行分析，从中进行变量查找，以获得类Edit，其中将会含有两个成员变量，即prew、next，因此是可能形成Edit类域对象网络的。通过网络分析，可以获得全部通过成员变量应用Edit类的类，并且从中能够得到在UndoManager中具有的成员变量，即undosFirst,undoslast,redosFirst和redosLast，为了使描述更加简单，本文对于存在的UndoManager对CompundEdit的引用并没有纳入考虑范畴。

为了进一步识别复杂网络中的异常情况，文章通过5个时间点划分，任意挑选10%的多源神经网络，反复进行复杂网络的分裂和合并实验。图2(a)(b)展示了算法ARMCN和算法DYNMOGA，FacetNet算法中的NMI和Error实验结果。从实验结果可以看出：在第1个时间点，ARMCN 算法相比于DYNMOGA算法和FacetNet算法更有优势。但ARMCN算法和FacetNet算法中的NMI实验结果几乎一样，ARMCN算法在复杂神经网络识别过程中可以有效地识别网络，除此之外NMI的数值保持在0.98以上。尽管DYNMOGA算法是从第2个时间点开始，NMI测试结果一直保持在0.96，但是ARMCN算法的错误率明显低于DYNMOGA算法和FaceNet算法,此项实验进一步验证了ARMCN算法可以高效、无误地识别复杂网络。

(a) 标准化互信息

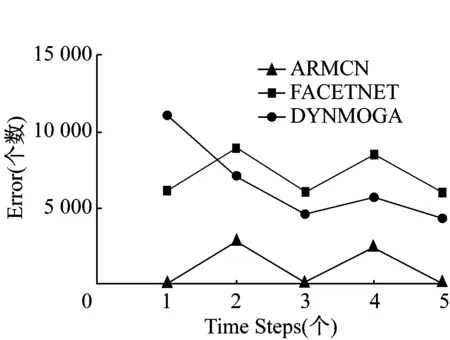
(b) 错误率图2 复杂网络

借用多源神经网络进行优化问题时，存在的主要弊端是运算时间比较长，另一个突出问题是需要反复进行适应度函数的运算。如果神经网络的数量增加到比较大的时候，此弊端将会进一步扩大，特别是在优化多源神经网络方面，此前的算法则更为复杂。本文提出的方法计算比较快，比较适合网络结构较大的神经网络,具体的计算如表1,表2所示。

表1 算法运行时间(g=50) s

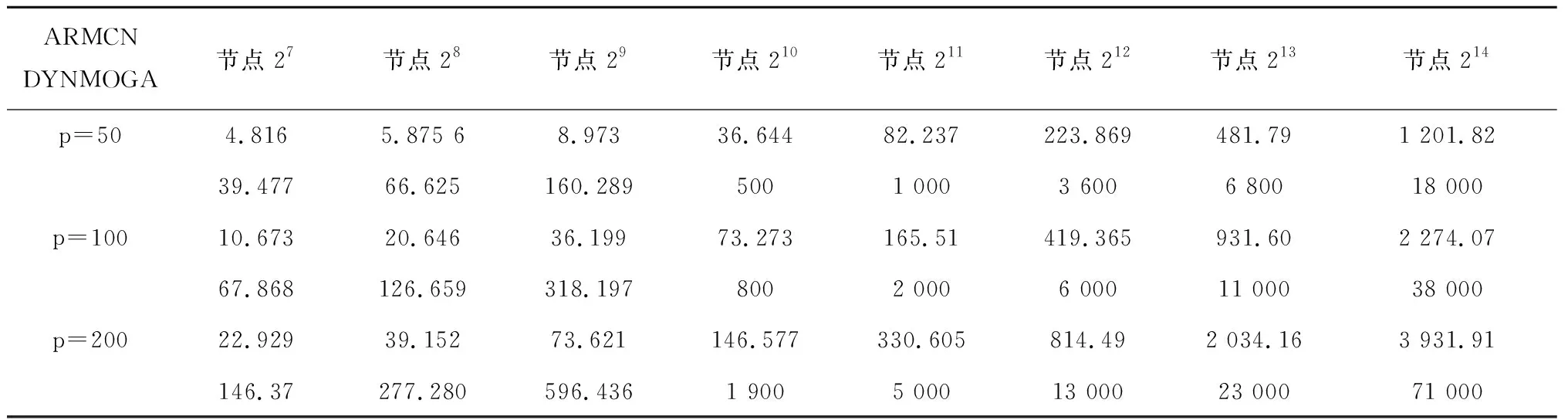
表2 算法运行时间(g=100) s

多源神经网络可以分为4个不同的神经网络，节点平均度数avgDegree=16,z=5,每个时间点上有10%的节点被选择进入其他神经网络,除此之外,节点数目n取值范围是{128,256,512,1 024,2 048,4 096,8 192,16 384}，对应的边m的改变范围是{1 938,4 018,8 184,16 158,33 026,65 256,131 388,285 782}。网络数量p的变化范围是{50,100,200}，迭代次数g的变化范围是{50,100}。从表1和表2实验结果可以看出：在一个时间点上，对应不一样的p,g组合，ARMCN算法和DYNMOGA算法的实验验证时间。特别是目前点数量成倍增长，ARMCN算法的内部使用明显低于DYNMOGA算法,DYNMOGA算法通常就是ARMCN算法运行时间的6倍左右。ARMCN算法的时间复杂度为O(gplogp×(n+m)),当在神经网络数量以及迭代次数确定的情况下，ARMCN算法执行时间呈线性增长。

3 结论

当前有关复杂网络关系的研究文献中，并没有将多源神经网络运用其中，因此，如果复杂网络运用当前的研究方法则无法进行有效分析。构建网络识别方法，基于该方法对复杂网络结构具有的一般特征进行描述,开展集中管理，针对实际中较为常见的一维无环网络进行分析，基于多源神经网络对网络进行扩展检测，以实现对不同寻常网络的有效追踪，进而分析在不同的异常网络下，对应情况进行及时处理。本研究还进一步剖析了为何将多源神经与异常识别视为复杂网络关系。本研究使用的多源神经网络算法，基于静态网络视角，使得识别设计网络具有更好的能力，也提高了识别结果的细致性以及准确性。