高等数学概念教学的教学策略探析与实践

陈艳平

(福建商学院 数学与计算机系，福州 350506)

一、概念教学的必要性与紧迫性

“以学生为中心”“因材施教”等教育理念都要求老师首先要了解自己所教的学生。我们分别统计了福建商学院经管类2016级与2017级文、理合班教学部分学生的高考数学成绩①。其中，高考数学(文)/(理)满分均为150分。2016级选取的是国际商务和电子商务2个专业共121位同学(文、理科生分别为66、55位)的成绩，成绩不区分全国卷与省卷，试卷分文、理；2017级选的是经济统计学、物业管理、会展经济管理等7个专业共609位(文、理科生分别为290、319位)福建籍且使用全国I卷的考生的成绩。高考数学各分数段的人数百分比及成绩分析,见表1、表2。

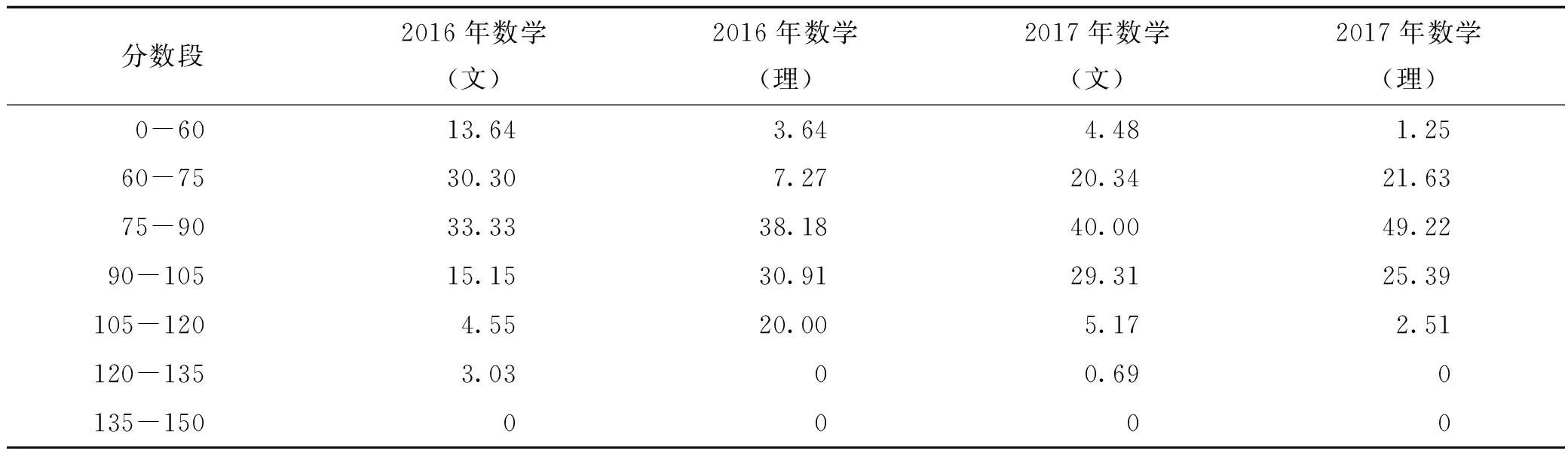
表1 高考数学各分数段的人数百分比

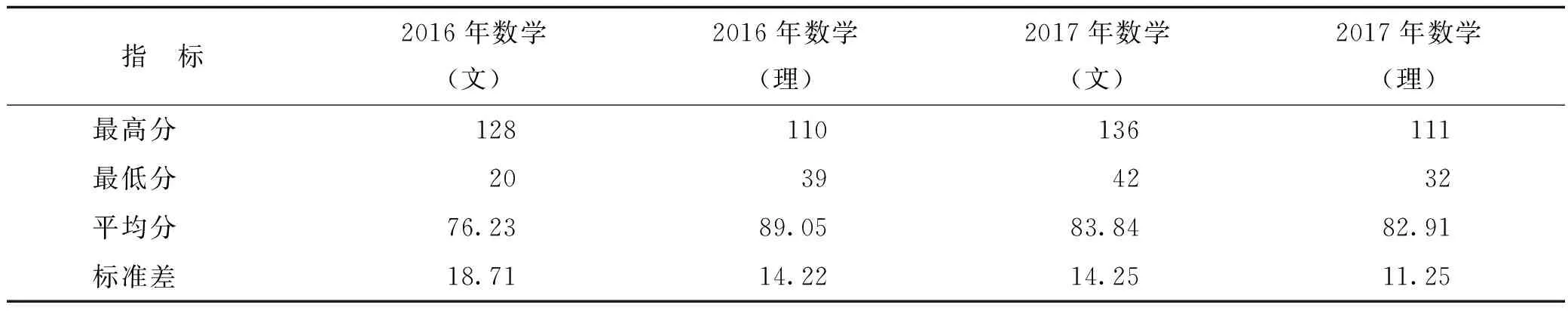
表2 高考数学成绩分析

从表1的数据可以看出，2016级及2017级的学生进入大学前的数学基础参差不齐。高考数学分数不仅文、理科差异明显，而且同科别的差异也很大。从表2的数据可以看出，不同个体的学习能力差异明显。2016年取得文科数学最高分128分、最低分20分的同学在同一个教学班(16国际商务2班)。同一个班的分数差距如此悬殊！其他班的数学基础同样良莠不齐。显然，在这样的教学基础下，实施文、理科生合班教学，不仅同学的学习压力很大，教师的教学压力也很大。怎么让学生在课堂上能坐得住、听得进、学得会，这是每一位高等数学任课教师面临的现实问题。

高等数学在培养学生的发散性思维、逻辑推理、定性分析等能力方面，有着其他学科无法比拟的优势，但其高度的抽象性、严密的逻辑性却让很多学生望而生畏。数学概念是人类对现实世界空间形式和数量关系的概括反映，是建立数学法则、公式、定理的基础，也是运算、推理、判断和证明的基石，更是数学思维、交流的工具[1]。

概念教学的重要性虽越来越受到关注，但仍然存在着诸多问题[2]83。从调查及访谈中，我们发现很多教师顾及到整体生源成绩参差悬殊性、班级学生学习基础的多层次性、文科与理科学生数学素质的差异性、教学课时的有限性及期末考试及格率等问题，为了减轻学生的学习负担，教学上习惯采用记结论略证明、重计算轻推理、多知识少思想的教法[3]58。在概念教学中，较多呈现教材中显现的知识逻辑，较少剖析概念背景及其蕴含的思想方法，没有很好地将高等数学知识与专业知识相融合。

二、概念教学的教学策略探析

概念教学，不能仅限于告诉学生“什么是”或“是什么”。概念教学包括形成概念、理解概念、应用概念、形成概念系、渗透数学思想方法等。

在数学基础多层次化的课堂上，教学的基本出发点是让每一层次的学生能不同程度地“亲近”高等数学，教师要在不多的课时内传授基本的数学知识，揭示数学本质，阐述思想方法[4]2。在概念教学实践中，首先要根据概念的类型与特点，采取恰当的教学方式，借助“微课”之力，帮助学生更好地理解概念的内涵与外延；其次，要照顾到各个层次学生的学习需求；第三，要兼顾文科生与理科生的学习基础、学习方法和思维等方面的差异。

(一)借力微课，形成概念

微课，它是以微视频为载体，是传统课堂学习的一种重要补充和资源拓展，满足学习者随时随地的学习需求和选择性学习的需要，是一种新型个性化学习方式和网络教研方式[5]。高等数学课程知识点多且内容抽象，而教学时数有限，学生的学习基础和理解水平有差异，因此可以将学习新知识时牵涉到的已知相关知识、需要预设的问题以微课的学习资源包提前呈现给学生。

陈述性的概念，比如极限。与有关数列的定义、数列通项的求法、考查某些数列an的通项an当n→时的变化趋势、考查函数f(x)分别当x→x0,x→时的变化趋势、与极限相关的数学文化、极限蕴含的思想方法、思考题等，教师都可以事先将它们上传到微课的学习资源包中。课前，让同学先感知、体验；课上，教师与学生共同归纳、形成概念；课后，通过微课中的微练习与微测试加以巩固、提高。这样，不同层次的学生可以按照自己的理解程度选择合适的步调学习，既减少了课堂上部分学生特别是后进生的学习焦虑感，又满足了优等生的学习需求，提高了整个课堂的效率，同时培养了学生自主探究与合作学习的习惯。

运算型概念，比如导数。课前，学生可以通过微课的学习资源，观察曲线上的某一割线绕一个定点转动的运动变化的动态图，思考割线的斜率与过该定点切线的斜率之间的关系，思考过曲线上某一点的切线斜率的方法，思考如何利用熟知的平均速度求变速运动的物体在某一时刻的瞬时速度的问题。课上，教师引导学生利用类比分析的方法提取它们的共性，引出导数的概念。

利用微课，学生可以根据自己的理解水平，控制学习的进程，减少对数学的畏惧感，相对轻松地形成概念。

(二)多样化教学，理解概念

在高等数学概念形成之初，学生对概念的理解不是很深刻，教师不要急于让学生记忆概念、陷入题海操练。在概念教学过程中，可以根据概念的特点，选择适当的教学形式与方法，帮助学生加深对新概念的认知，从而理解概念。

比如，函数的概念，通过设计下列练习，利用正反对比、类比等方法让学生明确概念的内涵与外延。

例1.判断下列对应是否为函数：

y=1;x+y2=1;x2+y=1;x2+y2=1;

y=arcsin(x2-2);y=arcsin(x2+2)。

在这些貌似非常简单且熟悉的情景中抛出问题，制造悬念，诱发与原有概念的认知冲突，激起学生强烈的探究欲望。让学生意识到对概念的本质内容的挖掘与理解不容小觑！当学生重新研读概念后，在各自思考的基础上由教师组织交流，并在教师引导下重新审视概念的条件、特征及结论，帮助学生加深对新概念的认知，学生豁然开朗后对概念的本质内涵的理解更加深入，实现了从感性认识到理性认识的升华，真正领悟了新概念的内容与实质，从而真正掌握概念。

又如，通过数形结合，利用整体与部分之间的关系，在对比分析中发现极值与最值概念的特征、性质、区别与联系；通过类比分析，得到导数与单侧导数概念之间的异同点；运用问题引申式，把不规则图形的面积转化为规则图形的面积近似和的极限，理解定积分的概念；运用同化式，利用已知定积分的概念帮助学生理解多重积分的概念等。明确概念的内涵与外延，深刻理解概念，能更好地培养学生的化归、迁移能力，提高学生分析问题与解决问题的能力。

(三)优化认知，运用概念

通过概念运用可以检测学生对概念的理解掌握程度。可以通过设置不同层次的练习，满足各个层次学生的需求。

以导数的概念为例。

首先，夯实基础，激发求知欲。从表1、表2的数据分析来看，有相当一部分学生的数学基础相当薄弱，以至于对概念的理解可能只停留在简单记忆的层次。教师要循序渐进地激励学生的学习，从概念教学入手，帮助他们梳理相关概念及知识点。

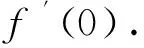
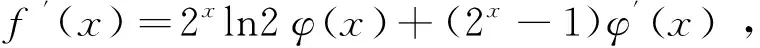
分析：题目中仅给出了函数φx在点x=0处连续，而函数连续不一定可导，所以在求导过程中不能用乘积求导法则，只能用导数的定义求导。

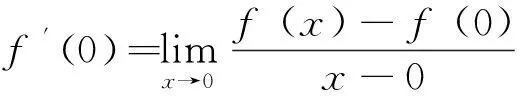
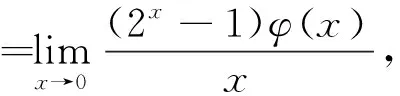
思考：设函数f(x)=x-aφx，其中φx在点x=a处连续且φa≠0,研究f(x)在点x=a处的可导性。

通过思考练习，达到辨析概念、举一反三、夯实基础、巩固提高的目的。

其次，加强应用，提高学习力。对班上的绝大多数同学，要求他们不但理解所学概念而且能较灵活地运用。

例3.当λ取何值时，函数

在点x=0处：(1)连续但不可导；(2)可导。

例4.设函数f(x)在点x=0处可导，且f(x)sinx，求证1.

用此类练习可以帮助学生理解新概念，温故知新，融会贯通所学知识。

最后，融合专业，拓展综合能力。从表1、表2的数据可以得到，有相当一部分学生的数学基础单薄。如何让这些学生能跟上教学进度，不掉队、不畏学，始终是授课教师要面对的严峻问题。在课堂教学过程中，选取与专业相关的实例，既能让学生理解并巩固所学到的高等数学的知识，又能促进今后专业课的学习，一举两得。比如可以将导数概念的后续相关概念与知识点预先设置到导数概念有关的思考题中。

例5.某银行准备新开设某种定期存款业务，假设存款额与利率成正比。若已知贷款收益率为r，问当存款利率定为多少时, 贷款投资的纯收益最高？

例6.已知在某企业某种产品的需求弹性在1.3-2.1之间，也就是，当价格上升1%时需求量下降1.3%-2.1%之间。如果该企业准备明年将价格降低10%，问这种商品的需求量预期可能增加多少？总收益预期可能增加多少？

类似这些看似简单的题更能激发学生的求知欲望。教师在学生急切知道求解方法的强烈心理需求下逐步引导学生探究问题，引发学生的深度学习。“学以致用”是学生课程学习的主要目的，也是高等教育培养应用型人才的必然要求[2]84。因此，在高等数学的概念教学中也要体现应用的理念。一方面，让数学的思想、研究的方法和着眼点更好地帮助学生理解经济问题中的基本概念和重要原理，让学生感受到数学不但来源于实际，而且应用于实际[3]60。另一方面，将数学概念与学生的专业相融合的教学设计，有助于学生正确理解数学作为学科基础课的作用，真实地感受到数学的魅力与价值，从而激发学习数学的兴趣性、自觉性与主观能动性，也为后续专业课的学习做好学习能力和思维能力上的储备。

综上所述，通过层层深入的练习与思考，精心设计，让每个层次的同学不仅能够夯实基础而且能找到适合自己学习目标层次的训练；通过应用题及富有启发性的思考题的操练，达到或提高学生学习的目标层次及灵活运用概念的目的；通过数学与专业知识的融合，增强学生学习数学的内在驱动力。

(四)挖掘关联，形成概念系

学生对概念的认知、理解、掌握，都需要过程。为了突破数学概念教学的瓶颈，关键就是要在理论上拓展关于数学概念学习的认识，挖掘概念学习的广度以及概念谱系之间的深层关联[6]。数学概念往往都不是孤立的，教师要善于引导学生学会系统地加工整理概念的方法，围绕某个概念构建概念关系网络图，辨析各相关概念之间的区别与联系，只有将新概念融入到原认知结构，在优化后的认知结构中理解掌握概念，才能实现知识迁移并灵活应用，从而培养学生的逻辑思维能力和系统观。

仍以导数的概念为例。导数考察的是函数关于自变量的瞬间变化率。学生对导数概念的到位的理解，有助于理解微分概念、可导与微分之间的关系及微分在近似计算中的作用。而微分是函数的线性化的方法，是后续介绍的利用微元法求平面图形的面积及立体图形的体积的理论依据，理解微分概念能为后续知识点及专业课的学习打好基础。在经济学中，经济函数的导数称为边际。边际概念是经济学中的一个重要概念，指的是经济变量的绝对变化率，而利用导数研究经济变量的边际变化的方法，就是边际分析法。学生对导数概念的到位的理解，有助于对后续学习中的边际成本、边际收益、边际利润等经济概念的理解，有助于利用边际分析法探究经济问题或进行决策。弹性概念是经济学中的另一个重要概念，指的是经济变量的相对变化率，用来定量地描述一个经济变量对另一个经济变量变化的反应程度。运用边际分析法与弹性概念能分别从微观和宏观方面把握经济的变化。学生对导数概念的到位理解，有助于理解微观经济学中相关概念及其经济意义，有助于对经济活动中的实际问题进行边际分析、弹性分析和优化分析，更好地为决策提供量化依据，为专业课的学习奠定良好的基础。

(五)渗透数学思想方法

高等数学的很多概念都蕴含着丰富的思想方法。例如，极限的思想，体现了从不变到变、从有限到无限、从量变到质变的辩证关系，是高等数学与初等数学的分水岭。导数与定积分是以函数为研究对象，都是通过局部取近似值，利用极限求精确值。微分是函数的线性化，是运用微分方法进行近似计算的基本思想。积分的“分割、近似、求和、取极限”是“化整为微、以直代曲、积微为整、去粗取精”的过程，这些思想与方法是处理很多工程技术常用的方法，更是处理经济问题中的连续复利、现金流、将来值、已知经济量的边际函数求总量、利润最大、成本最低等问题的基本方法。

以概念教学为抓手，才能吸引学生在课堂上的注意力，持续学习，深入应用，接受必要的数学思维方法的熏陶。学生经过数学思维方法训练后，更容易理解、消化相应的经济原理及经济概念，从而更好地为专业课的学习奠定坚实的基础，数学思维方法的积淀能让学生受益终身。

三、概念教学的实践成效

高考数学成绩不太理想的同学，数学基础较薄弱，学习高等数学会更费心费力。考察从2016年9月至今笔者任课的8个文、理科生合班教学的概念教学的实践情况，2016级同学的成绩用数组(a，b，c)表示，其中a、b、c分别表示2016年高考数学文(理)、2016-2017-1高等数学I、2016-2017-2的高等数学II的成绩(满分分别是150、100、100分)。高等数学I/II试卷不分文理，全校统考，在这里平均分的算法与期末试卷分析的算法不同，仍按入学时的文/理生源分别计算文/理科生期末成绩的平均分。原高考文/理科分数最低的2位同学对应的成绩数组分别为(20， 18， 86),(28， 66， 68)/(39， 70， 63),(50， 83， 57)， 文/理科平均分为(76.2， 71.4， 61.3)/(89.1， 83.5， 69)。2017级同学的成绩用数组(m，n)表示，其中m、n分别表示2017年高考数学文(理)、2017-2018-1高等数学I的成绩(满分分别是150、100分)。在2017级，选取2个班的文科高考数学成绩均是66分的同学各2位，对应的成绩数组分别为：(66， 65),(66， 92)/(66， 88),(66， 92),平均分数组分别为 (81.8， 69)/(86.1， 83.5)。选取理科成绩最低的2位同学，对应的成绩数组分别为：(59， 88), (64， 95)/(32， 95),(69， 90)，平均分数组分别为(85.1， 83.0)/(86.1， 85.5)②。

分析2016级及2017级被调查班级学生文/理平均分的数组，说明文、理科生的思维方式、方法的差异是不争的事实，文、理科生对数学知识的接受能力的差异也是不争的事实，但从被调查学生的成绩数组可以看出高考数学成绩并不能决定高等数学的成绩。虽然学生学习高等数学普遍感到困难，学习动机不强烈[4]14，但大部分同学想学好高等数学这门课程，包括一些数学基础相对薄弱的同学。教师要准确把握文、理科生的不同特点，以概念教学为契机，关注学生学习高等数学的全过程，帮助他们克服心理上的焦虑恐惧，战胜学习上的畏难情绪，化“被动应付”为“主动应对”，当他们对数学概念的理解能力有一定提高后，学习迁移能力及数学应用意识也会得到一定程度的提高。从2016、2017级的被调查学生的成绩数组看出，基础相对薄弱的同学只要从概念的理解与掌握入手，就可以学好高等数学。概念教学也是教师帮助学生提高学习能力的一个突破口。面对数学基础参差不齐的事实，高等数学文、理科生合班教学需要教师坚持不懈地对教材策略进行探究，需要教师对学生不间断的督促指导，更需要师生之间的长期协作与相互协调。

四、结 语

概念性的理解有助于解题技巧的掌握，基于概念的教学方法在保证学生解题技巧的同时加深了学生的理解，理解和掌握的知识与程序性知识相比更容易推广到陌生的领域[4]39。科学的概念教学能帮助学生更好地理解概念或概念所蕴含的思想方法，更好地理解与掌握所学知识，更好地提高学生的知识正迁移和实际应用能力，更好地帮助学生理解相关学科的理论体系，为学生后续课程的学习打下基础。

在课堂概念教学上，既要考虑到概念的类型特征，又要考虑到学生的理解接受差异。教学方式要多样化，教学内容要多层次化，教师要引导学生掌握概念的内容、理解概念的内涵和外延、领悟概念所蕴含的思想方法，激发学生主动参与教学过程的积极性，从而更好地帮助学生理解知识、拓展思维、培养能力。

注释：

①高考分数原始数据来源：福建商学院招生办。

②期末分数数据来源：福建商学院教务系统。