基于负载转矩观测器的永磁同步电机积分滑模控制

金鹏飞，谢 源，王 杰，肖立健

(上海电机学院，上海 201306)

0 引 言

永磁同步电机(以下简称PMSM)具有体积小、功率密度大等优点，因此被广泛应用于高速、高精密运动控制领域[1]。常规的PID控制虽然在线性控制中有较好的控制效果，但PMSM是一个强耦合、非线性的系统，因此很难满足伺服系统的控制要求[2,14]。

目前，国内外学者提出了许多智能控制方法来提高PMSM的控制性能。其中观测器法[3-5]、模糊控制[6]、自适应控制[7]、滑模控制[8-11,14]都取得了较好的控制效果。其中滑模变结构控制与控制对象参数和扰动无关[12]，在非线性、强耦合的PMSM中有较好的应用前景。文献[3，4]采用了观测器法，通过对负载扰动进行实时观测，并将观测值输入至控制器中，从而对转矩电流进行补偿，提高了系统响应速度，但该方法对系统参数具有较强依赖性。文献[5]将负载观测器与滑模控制相结合，提高了系统的响应速度与抗扰性,但该观测器测度较慢。文献[6]采用模糊控制器实时调节PI参数，提高了系统的鲁棒性和响应速度。文献[8-11]对滑模面和滑模控制律进行了改进，当系统存在扰动时，通过补偿和改进趋近律的方式提高了系统抗扰动性能和稳定性。文献[13]用模糊控制器修改滑模控制律的指数项系数，提高了系统响应速度。

本文采用观测器代替硬件设备进行转矩观测，在传统负载转矩观测器的基础上，增加了状态反馈误差的微分项，提高了负载转矩观测器的跟踪速度，同时针对PMSM的抗扰动性，采用了积分滑模面的方法，并设计了一种新型的指数趋近律，提高了系统的响应速度，增强了抗扰动性能，且能够有效抑制滑模控制的抖振。

1 PMSM的数学模型

PMSM在d，q轴的数学模型如下：

(1)

式中：ud,uq分别为d,q轴电压；id,iq分别为d,q轴电流；Ld,Lq分别为d,q轴电感；Ra是定子电阻；λ0为永磁体磁通；ωe为转子电角速度。

表贴式PMSM的d，q轴电感相等，故电磁转矩方程式：

Te=1.5piqλ0

(2)

电机转动方程：

(3)

式中：ωm为PMSM机械转速；J为转动惯量；p为电机极对数；b为阻尼系数；Te为电磁转矩；Tl为负载转矩。

2 负载转矩观测器

设系统状态方程：

(4)

传统龙伯格负载转矩是以积分的形式被观测的，因而收敛速度较慢。为提高负载转矩的观测速度，在观测器中引入状态反馈误差的微分项[4]，如式(5)所示：

(5)

由式(4)、式(5)可得：

(6)

(7)

根据期望的极点α,β，假设b=0，且k1=k3=0，则：

(8)

将k1,k2,k3,k4代入式(5)可得：

(9)

由式(9)可得改进负载观测器结构图，如图1所示。

图1 改进负载转矩观测器结构图

3 积分滑模面的设计

3.1 滑模面的选取

通常将速度和加速度的误差作为滑模控制的输入，加速度一般由速度的微分得到，而微分会导致噪声信号的放大，从而导致加速度信号误差较大[2，11]。因此，本文采用一种积分滑模面，将速度和速度的积分作为滑模控制器的输入，可减小转速波动对系统造成的影响。

在速度环中，误差：

(10)

系统变量：

(11)

通过引入状态变量的积分量，可得积分滑模面：

(12)

3.2 趋近律的求取

将式(12)微分后，可得：

(13)

常见指数趋近律的一般形式如下：

(14)

式中：ks是指数趋近项，当s较大时，系统状态能有较大速度趋近滑模面；εsgn(s)是等速趋近项，当s趋近于零时，趋近速度为ε。

本文在指数趋近律的基础上提出了一种新型指数趋近律：

(15)

(16)

式中：ρ≠0，δ>0，取ρ=-5，δ=1，可得函数曲线如图2所示。

图2 Y(s)，sat(s)和sgn(s)开关函数

从图2中可看出，当ρ=-5，δ=1时，函数Y(s)相对于饱和函数sat(s)更加平坦，且随着ρ，δ取值的不同，有不同的作用效果，可根据实际选取合适的值，以满足工程需求。

由式(3)、式(10)、式(13)可得：

(17)

结合式(15)、式(17)可得：

(18)

由式(18)可看出，通过负载转矩观测器将观测值反馈至转矩电流中，控制器能快速响应负载变化。同时减小了对趋近律参数值的需求，因而减小滑模控制增益的幅值，可削弱抖振现象。

3.3 滑模控制器稳定性分析

为分析滑模控制稳定性，选取Lyapunov函数：

(19)

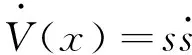
(20)

由式(17)、式(20)可得：

(21)

由式(21)可知，改进的滑模控制律满足Lyapunov定理，保证了系统可以进入滑动模态。

4 仿真实验

为验证基于负载转矩观测器的PMSM积分滑模控制方法的有效性，利用MATLAB/Simulink搭建id=0磁场定向的矢量控制的PMSM的控制模型，如图3所示。

图3 系统控制模型

图3中，电流环采用了传统的PI控制器，在速度环中采用了积分滑模控制器代替了传统的PI控制器。同时采用了改进的负载转矩观测器，将负载转矩观测器的输出作为积分滑模控制器的输入，可对转矩电流iq补偿，既可以避免硬件测量给系统带来的影响，又可以提高系统的响应特性。

永磁同步电机的参数：极对数p=4；永磁磁链ψf=0.175 Wb；阻尼系数b=9.44×10-5N·m·s；d，q轴电感Ld=Lq=8.5×10-3mH；转动惯量J=3.6×10-4kg·m2；定子电阻Ra=2.87 Ω。

在仿真实验中，PMSM空载起动，在0.2 s时给系统一个5 N·m的负载。仿真波形如图4～图8所示。

图4 负载转矩跟踪图

图5 转速曲线图

图6 起动时转速放大图

图7 0.2 s时转速局部放大图

图8 转速波动图

图4中，改进的负载观测器能够快速稳定地跟踪负载的变化，且无超调。这种软测量技术代替了传统的仪器测量，不仅节约了系统成本，且增加了系统的稳定性。

图5是在仿真时间0.3 s内，PMSM的转速波形图。图6、图7分别是起动以及0.2 s时电机转速的局部放大图。图6中，本文的控制策略在空载起动时无超调，且调节时间短。图7中，系统在受到扰动时，本控制策略在转矩电流补偿和积分滑模控制下，恢复时间只需0.002 s，而PI控制恢复转速需要0.02 s。且下降转速为31 r/min，而PI控制器下降转速为60 r/min，转速下降明显变少。因此，本控制策略能够在扰动情况下，更快速稳定地使电机达到设定转速。

当转速稳定后，从图8中可看出，采用Y(s)函数代替原来的符号函数sgn(s)，转速波动范围在1 r/min以内，可以减弱滑模控制固有的抖振问题。

5 结 语

本文在PMSM矢量控制的基础上，采用积分滑模控制器代替了传统转速环的PI控制器。为减小负载扰动对电机转速的影响，采用了改进的负载转矩观测器，对转矩电流进行补偿，避免了负载转矩的直接测量，减少了系统成本。同时采用改进的指数滑模趋近律，并用Y(s)代替传统的符号函数sgn(s)，提高了系统的响应速度和抗扰动性，减小了系统的抖振，具有一定工程意义。