基于BP神经网络的曲轴润滑特性全局优化*

王振 白杨郝长利 杜建秋刘为 刘丽娜李腾

（1-天津大学内燃机研究所 天津 300072 2-天津经纬恒润科技有限公司）

引言

近年来，日益严苛的油耗法规与柴油机强化程度的不断提升，使得轴系润滑与磨损问题成为设计开发关注的焦点。国内外学者对于轴系润滑特性的研究表明：轴承间隙、轴颈直径、轴颈和轴瓦表面粗糙度、供油孔角度及大小等因素都会对轴系润滑特性产生较大影响，单独从其中某一因素进行轴系润滑特性分析可以深入揭示单一因素的作用机理，但获得最佳的轴系润滑特性需要综合考虑各因素的影响[1-4]。良好的润滑特性应满足最小油膜厚度、峰值总压和峰值粗糙接触压力的限值要求；为提高发动机热效率，需要尽可能多地减小摩擦损失功率[5-6]；基于可靠性的角度考虑，轴系的设计应具备改善轴瓦表面点蚀现象的能力，大量试验结果也表明，轴颈的高速离心与向心运动会使轴瓦表面产生点蚀，造成合金疲劳脱落；而且利用最大剪切率作为评价指标的油膜振荡也会对轴承润滑特性产生较大影响[7-9]。

本文基于课题组与企业合作开发的某款增压柴油发动机，针对最大爆发压力提升情况下出现的主轴颈润滑恶化现象，在不对轴系结构做重大改动的基础上，采用最优拉丁超立方实验设计与BP神经网络相结合的方式，建立轴系弹性流体动力润滑近似模型，综合考虑各影响因素对曲轴各主轴颈的作用，从全局角度对各评价指标结果进行加权寻优，从而获得轴系最佳润滑特性设计参数优化各轴颈润滑状况。

1 弹性流体动力润滑控制方程

1.1 扩展Reynolds方程

基于质量守恒边界条件，考虑润滑油填充率的影响，可推导得出扩展Reynolds方程[10]：

式中：x、z分别为轴承展开周向和轴向坐标；λ为滑油填充率；h为油膜厚度；η为滑油动力黏度；p、pc分别为油膜压力和空穴压力；u1、u2分别为轴颈和轴瓦的周向速度；t为时间。

1.2 油膜厚度方程

不计轴瓦变形时，名义油膜厚度方程为[11]：

式中：C为半径间隙；e为偏心距，θ为由轴承上方垂线计量的角度；θ=x/R，R为轴承孔半径；θξ为偏位角。

计入轴颈、轴瓦变形后，油膜厚度方程变为：

式中：hj和hs分别为轴颈和轴瓦的弹性变形引起的油膜厚度变化量。

1.3 微凸峰接触理论

因为曲轴主轴颈与轴瓦之间主要处于混合润滑状态，存在微凸峰接触压力pac，运用Greenwood-Tripp 理论求得[12]：

式中：β为微凸峰曲率半径；ν1、ν2分别为轴颈、轴瓦泊松比；E1、E2、E*分别为轴颈、轴瓦和当量弹性模量；σ1、σ2、σs分别为轴颈、轴瓦表面的粗糙度及两表面的综合粗糙度。

1.4 主轴承负荷

主轴承负荷Fb包括油膜负荷Fo和微凸峰负荷F，即

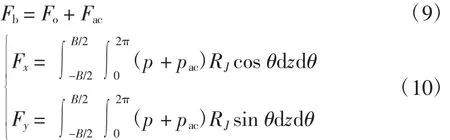
式中：B 为轴承宽度；RJ为主轴颈半径；Fx、Fy分别为轴承负荷在x、y方向上的分量。

2 弹性流体动力润滑建模仿真

本文所用增压柴油发动机基本参数如表1所示。图1为整机有限元网格模型，在进行多体动力学建模前，需对其中的机体缸盖、曲轴、连杆等部件分别保留前60阶模态进行缩减。因为主要考虑主轴颈的润滑状况，所以在搭建模型时只对主轴瓦与主轴颈之间的连接副采用EHD2单元，而对于连杆轴瓦与连杆轴颈之间的连接副采用REVO单元。其余各连接副参数依据AVL公司推荐公式以及整机具体设计参数计算得到。

表1 发动机技术参数

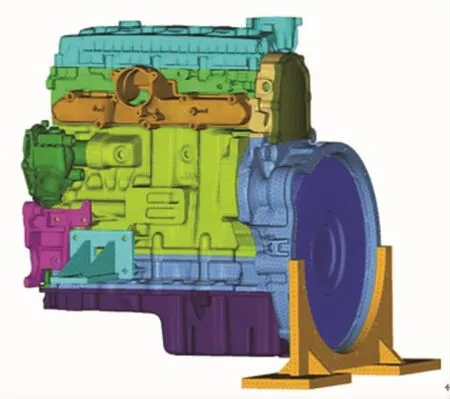
图1 发动机有限元模型

表2 轴系参数

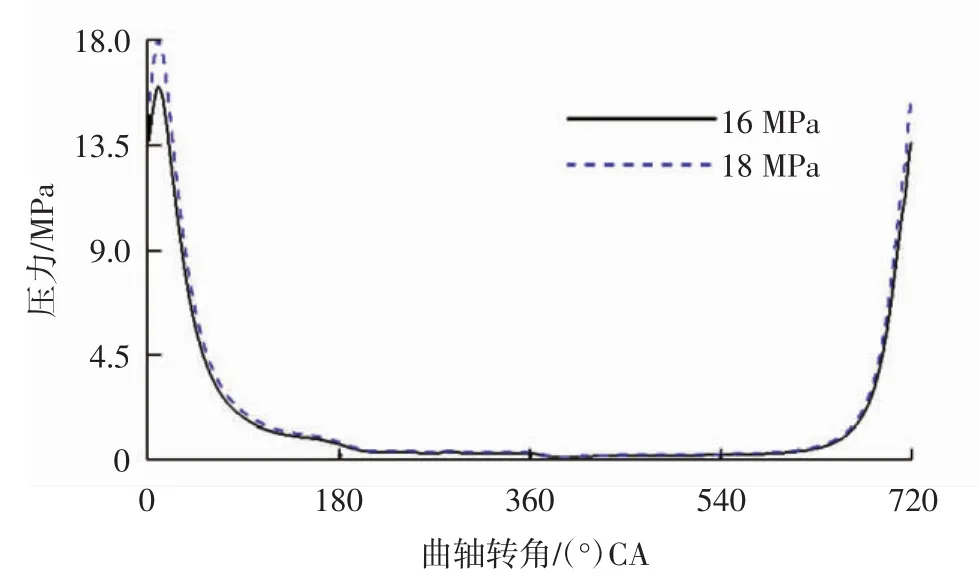
图2 缸压曲线

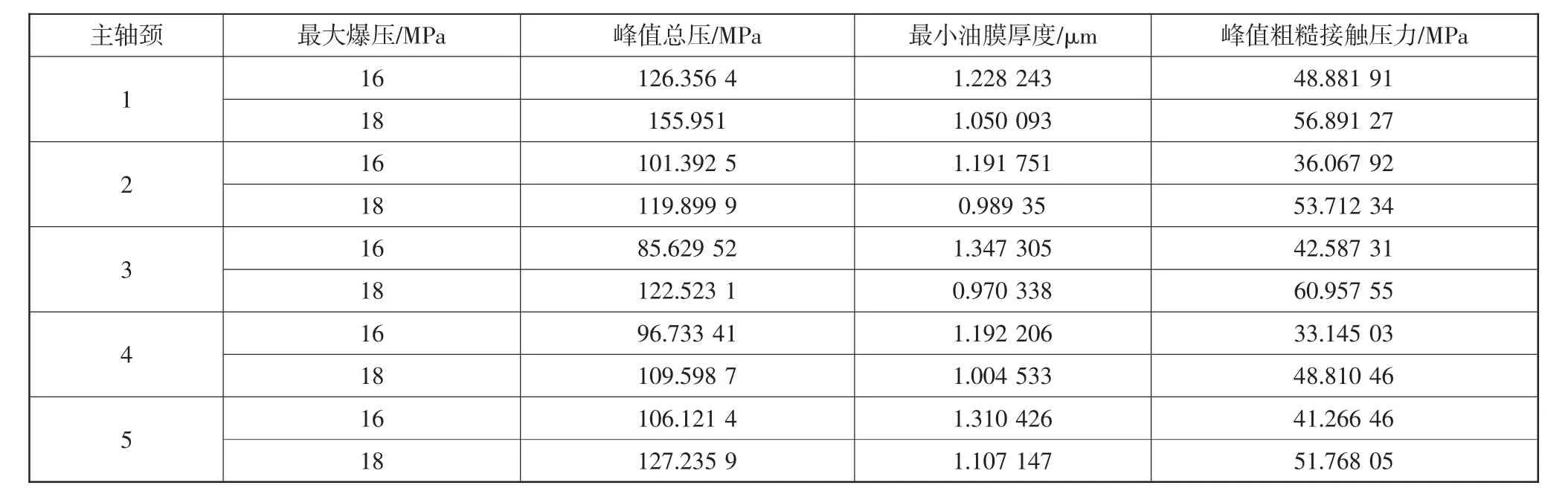
表3 曲轴润滑计算结果

依据搭建的多体动力学模型，分别对标定工况最大爆发压力为16MPa和18MPa 2种情况下的曲轴主轴颈润滑特性进行计算。轴系具体参数如表2所示，缸压曲线如图2所示，部分评价指标结果如表3所示。

从表中可以发现，最大爆发压力增加后，各主轴颈峰值总压、峰值粗糙接触压力都出现增加趋势。依据峰值总压220MPa、峰值粗糙接触压力60MPa的限值要求可以判定除第4主轴颈的峰值粗糙接触压力外，各主轴颈都能满足润滑要求。另外，各主轴颈最小油膜厚度都出现一定幅度的下降，第2、3主轴颈最小油膜厚度小于1μm，不满足最小油膜厚度大于1μm的要求。因此，爆发压力增加后，原始设计参数下曲轴润滑无法满足要求，需要进行优化改进。

该机型设计初期在强度方面留有较大裕度，即使在爆发压力提高的情况下疲劳寿命也能满足要求，所以在爆发压力提升后不用针对强度需求对曲轴结构做重大改动。而对于曲轴润滑特性优化，相关研究成果表明，改进轴承间隙、轴颈和轴瓦表面粗糙度、供油孔角度和大小以及供油压力等参数即可明显改善曲轴润滑状况[14-15]。因此，本文选择从这6个方面进行优化方案设计，各参数取值范围以及取样水平个数如表4所示。通过取样水平可知，6个参数排列组合产生的全部方案数接近40万，考虑到单个方案动力学计算耗时较长，为最大限度减小计算量并且保证计算结果的准确性，本文选择采用最优拉丁超立方实验设计结合BP神经网络的方式进行优化方案设计。首先采用最优拉丁超立方实验设计选取110个样本进行动力学计算，然后利用BP神经网络强大的非线性能力[16]，基于弹性流体动力润滑计算结果，建立各影响因素与评价指标间非线性关系的近似模型用于替代多体动力学模型，最后依据近似模型进行设计参数寻优。表5为选取的部分样本及第二主轴颈弹性流体动力润滑计算结果。

表4 优化变量参数

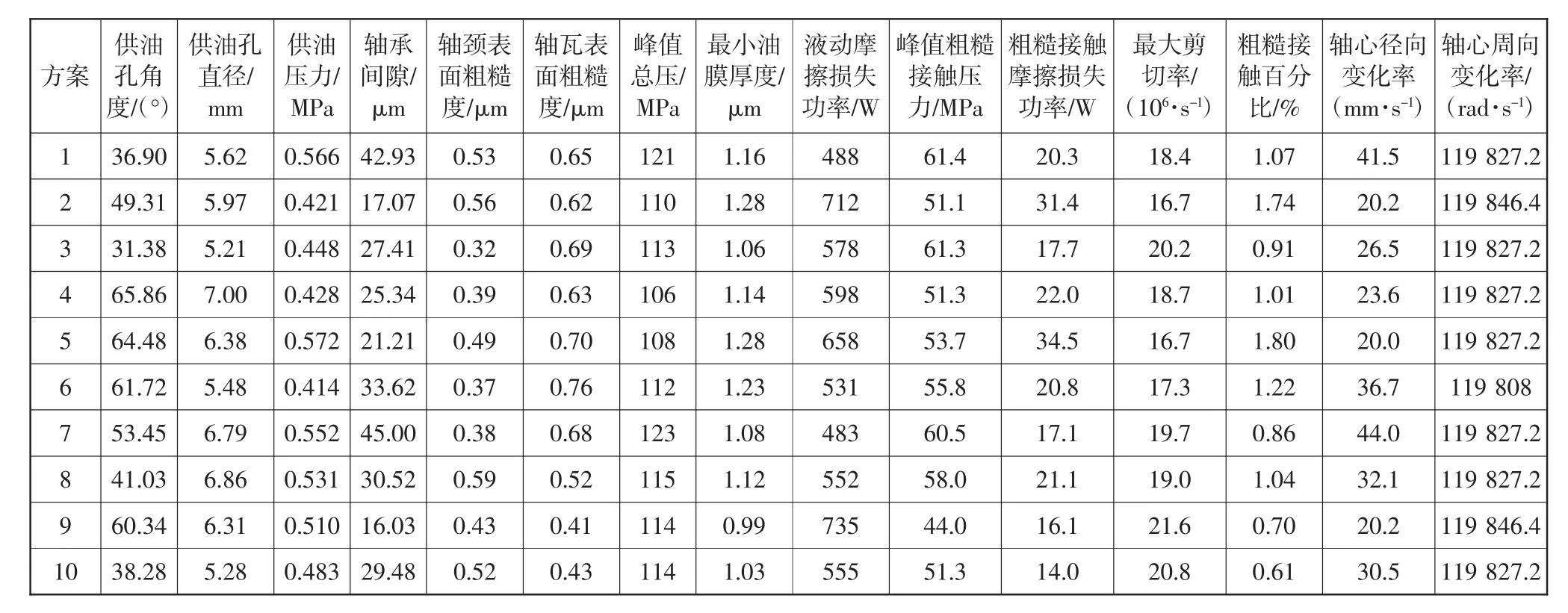
表5 第二主轴颈计算结果

3 BP神经网络训练及优化结果选取

由于取样数据（输入）与评价指标结果数据（输出）数量级差别较大，会对隐含层各节点权值的选取造成一定的影响，为消除不利影响和提高神经网络训练的收敛性，需要对输入输出数据进行归一化处理，本文选择使用MATLAB自带函数mapminmax将数据处理为介于[-1，1]之间的数值。

为充分利用样本数据以及保证训练得到模型的准确度，本文选择利用交叉验证的方式进行神经网络的训练，利用其中70%的数据进行训练，15%的数据用于进行验证，剩余15%的数据用于测试。

因一层隐含层的神经网络模型就具备很强的泛化能力与良好的预测精度，并且结构相对简单，本文选择使用一层隐含层的神经网络模型进行样本训练和预测，其中隐藏层采用S对数传递函数，输出层使用线性函数，学习算法采用Levenberg-Marquardt。同时，为保证神经网络模型训练的准确度并避免过拟合的问题，在综合考虑模型训练、验证、测试的全局线性系数R和训练模型均方根值的基础上，会尽量选择较少隐含层神经元数的模型作为最终的预测模型。

通过对隐含层不同神经元数训练结果的对比分析，最终确定隐含层神经元数为10，模型最终训练、验证、测试的全局线性系数R分别为0.990 17、0.985 07、0.988 89、0.989 23，均方根值为 0.009 00。如图3a、b所示。通过对原始结果与样本输入通过训练模型计算得到的结果对比发现，除个别点存在较大误差外，剩余数据的误差都在7%范围内，可以认为神经网络训练模型具有较高的可信度。

依据表4优化变量取值区间及取样水平建立优化参量组合方案的全因子矩阵，然后利用神经网络训练模型计算得到对应结果，并进行反归一化操作作为评价指标实际结果。对于获取的结果，首先根据粗糙峰值接触压力小于60MPa、膜厚比介于1~5之间以及峰值总压小于220MPa 3个强制限值条件过滤掉方案中不合格结果。虽然神经网络训练时存在较小误差，但这部分评价指标的结果大多处于限值条件附近，不在理想润滑方案之列，不需要对限值条件进行缩放处理。另外，本次优化的目的是在保证曲轴润滑合格的情况下降低摩擦损失同时减小磨损、改善穴蚀以及油膜振荡，所以对于剩余结果，本文先选择从摩擦损失功率方面进行优化方案选取，根据各主轴颈粗糙接触摩擦损失功率和液动摩擦损失功率获得各方案整个曲轴摩擦损失总功率，并选取其中前5%作为下一步优化备选方案。接着对备选方案各主轴颈最大剪切率、粗糙接触百分比、径向最大变化率以及周向最大变化率结果进行加权运算，考虑到各评价指标结果数量级不一样，先计算获得各方案相同主轴颈相同评价指标在剩余结果中的比重，然后对各方案所列4个评价指标按照比重值进行加权运算。考虑到上述4个评价指标没有明确的量化关系，而本文希望对设计方案基于所列评价进行全局优化，因此将所列评价指标的权重系数均设为1。依据各评价指标对曲轴润滑特性的影响属性判断，最终优化方案应该是每个方案所有结果加权以后的最小值。表6为加权后选取的五个最优方案。

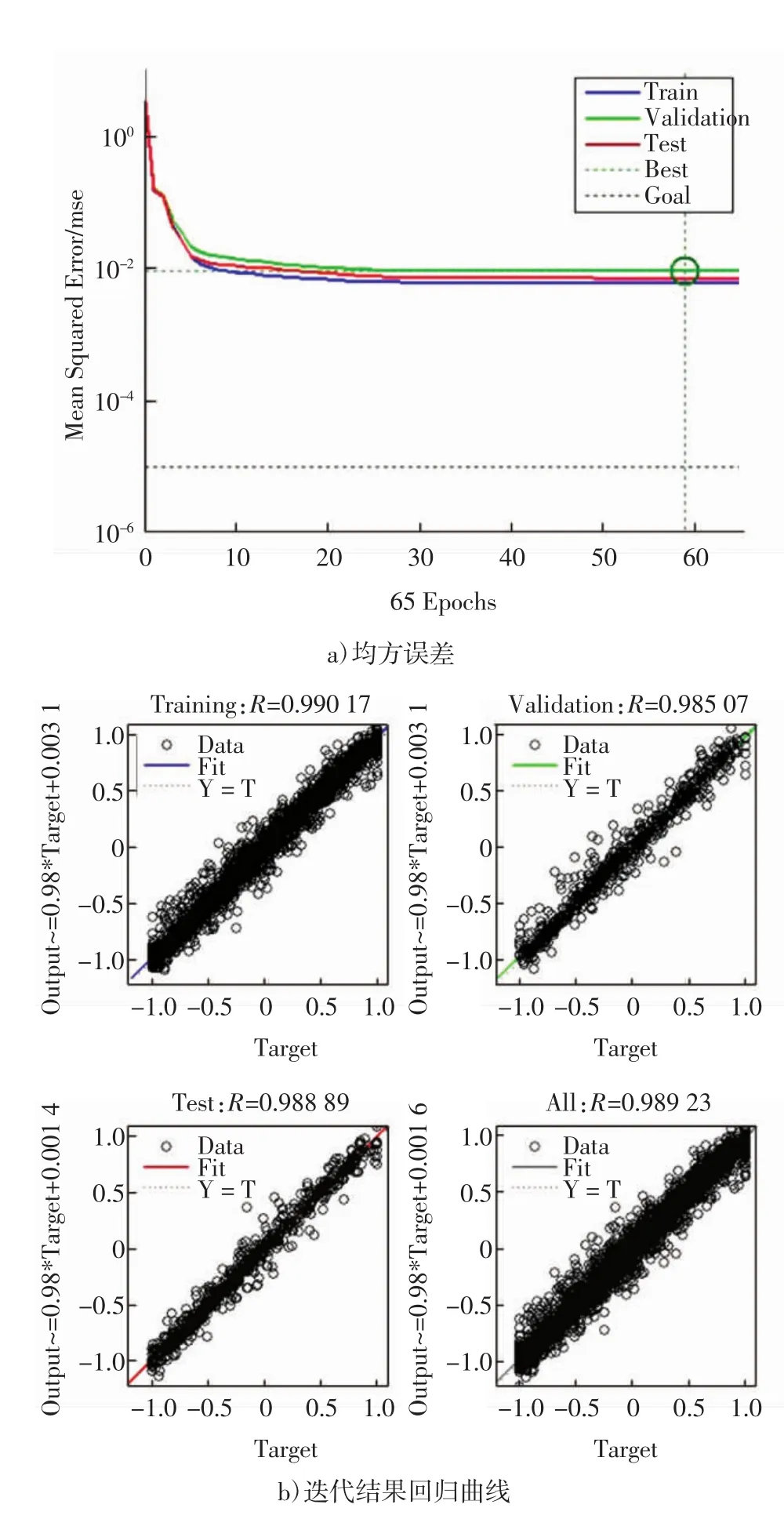
图3 BP神经网络训练结果

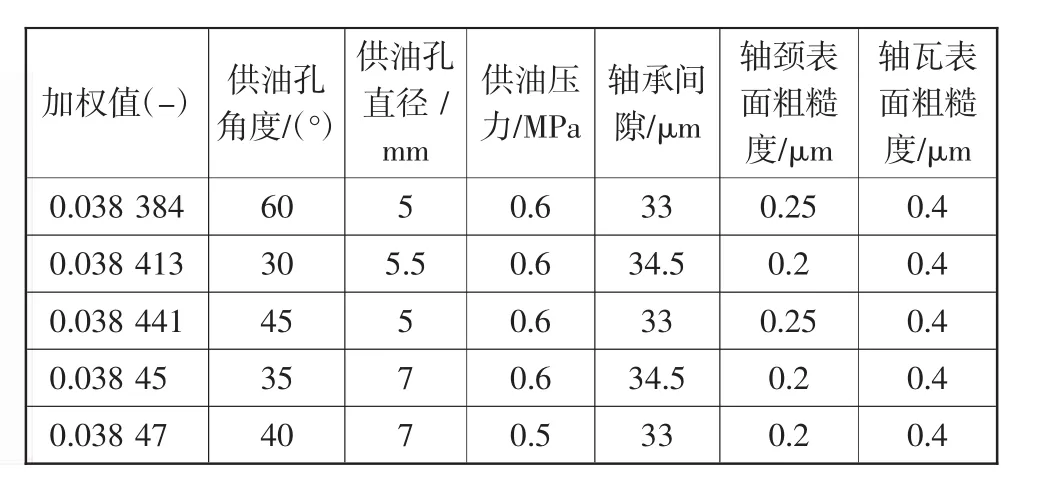
表6 加权优选方案

根据表6数据，选择加权值最小的方案进行弹性流体动力润滑计算，并将计算结果与原始设计16MPa和18MPa的各项结果从以下两个方面进行对比分析。

4.1 摩擦损失

摩擦损失主要从液动摩擦损失功率、粗糙接触摩擦损失功率、粗糙接触百分比3个方面进行比较，具体数值如表7所示。

从表7可以看出，优化方案在18MPa的最大爆发压力下的液动摩擦损失功率、粗糙接触摩擦损失功率以及粗糙接触百分比明显优于同爆发压力下的原始设计方案。相比于原始设计16MPa，优化方案虽然总体摩擦损失略大，但增加幅度只有1.5%，而且在某些主轴颈上液动摩擦损失功率与粗糙接触摩擦损失功率略优于原机设计。同时，在粗糙接触百分比方面，优化方案所有主轴颈都优于原机。据此也可以判断出，在某些主轴颈上粗糙接触摩擦损失功率较大主要是由峰值粗糙接触压力增加引起的。

4.2 油膜振荡与轴心运动

油膜振荡主要依据最大剪切率进行比较，轴心运动主要从轴心径向和周向最大变化率以及轴心运动轨迹进行分析。具体数值如表8所示。

4 最优方案计算结果分析

表7 摩擦损失

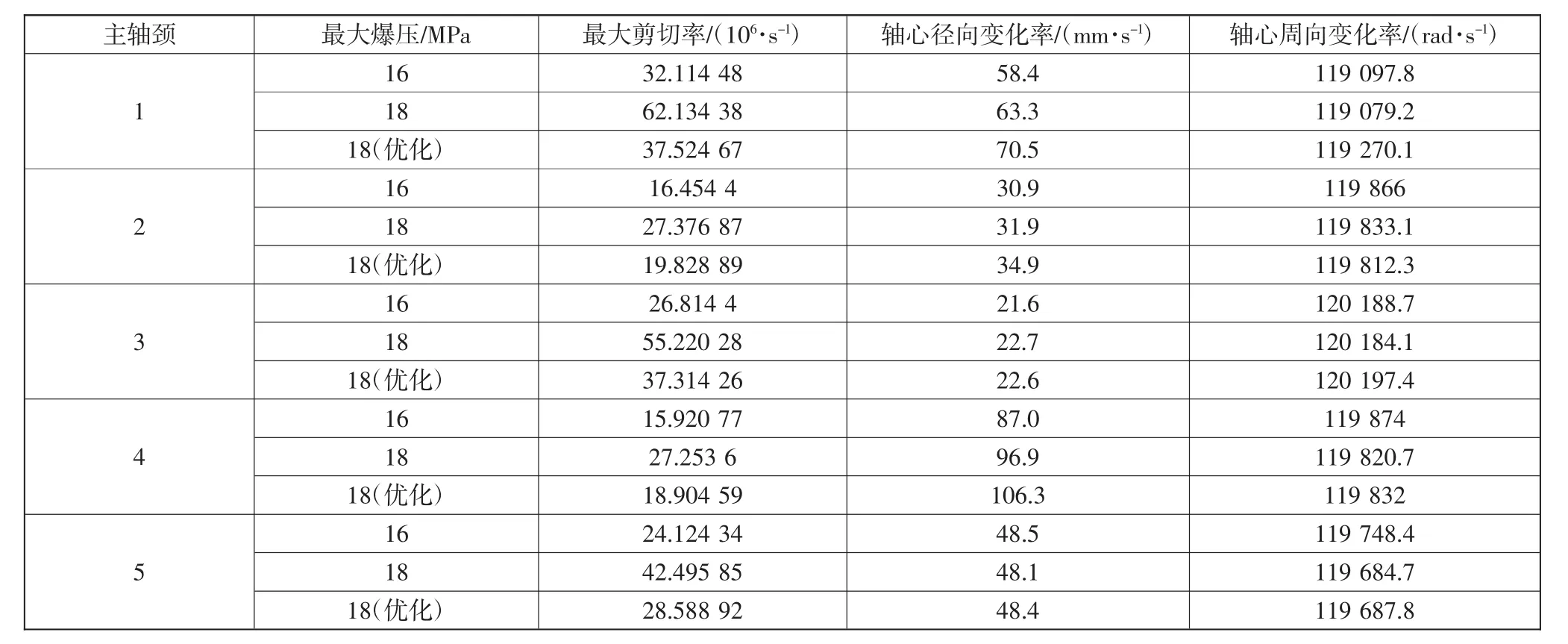
表8 剪切率与轴心运动

从表8可以看出，优化方案在最大剪切率方面大幅优于原机设计方案在18MPa时的情况，稍大于原始设计方案16MPa，对比文献[4]中优化方案最大剪切率数值可知，优化方案油膜振荡能够得到有效遏制；轴心周向最大变化率所有方案基本相同，可以认为周向运动优化方案能够满足使用要求：从轴心径向最大变化率方面看，虽然优化方案总体上大于原机18MPa和16MPa，但优化方案所有主轴颈都小于第四主轴颈16MPa时的数据，可以认为，除第4主轴颈外都满足轴心径向最大变化率的要求。为了更加准确地判断优化方案第4主轴颈轴心径向运动，选取了3种状况下的轴心运动轨迹进行分析，如图4所示。

虽然第4主轴颈优化方案在径向变化率方面相比原始设计16MPa增大约22.3%，但是从上面的轴心轨迹图可以看出，三者的运动趋势基本相同，轴心运动轨迹中离心与向心运动较明显的区域大体相似，可以认为优化方案满足要求。

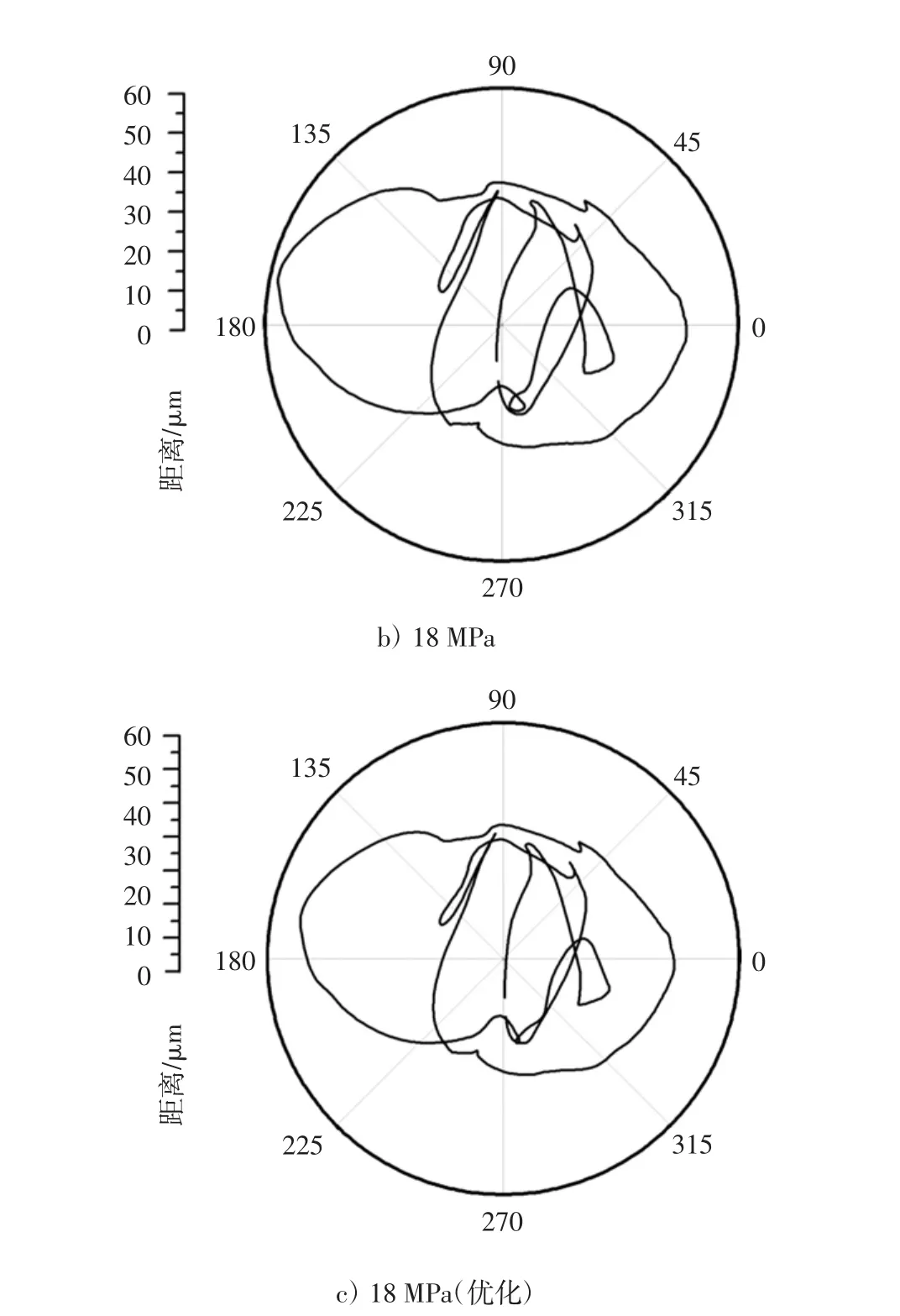
图4 轴心轨迹

根据上述分析可以发现，对4个变量进行同时优化会存在一定取舍，很难保证每一个变量都达到最优，但本文所使用的优化策略会优先考虑变化最为明显的变量，当然也可以通过增加变化不太明显变量的权重系数来进行优化参数选取，但是这样必定会弱化变化明显变量的优化效果。因为本次优化结果已经达到预期目标，所以不需要调整权重系数进行再次优化。

5 结论

1）利用最优拉丁超立方实验设计结合BP神经网络建立的曲轴弹性液体动力润滑近似模型具有较高的精度，能够替代多体动力学模型进行优化分析。

2）通过近似模型得到的优选方案，总摩擦损失功率大幅优于原机18MPa，仅比原机16MPa高约1.5%。

3）全局优化得到的优选方案在部分评价指标上能够得到优于原机16 MPa的结果，但是对于部分变化不够明显的评价指标，会出现略差于原机18 MPa的结果。优化方案总体结果接近原机16 MPa，达到预期优化目标。