对流扩散方程的迎风间断有限体积元方法

陈凡，徐之晓

(1.枣庄学院 数学与统计学院，山东 枣庄 277160；2.齐鲁理工学院 计算科学与信息工程学院，山东 临沂 277722)

0 引言

考虑对流扩散方程

(1)

其中u(x,y,t)是有界区域Ω⊂R2上的未知函数，边界∂Ω是分段光滑的，其中∂Ω=∂Ω+∪∂Ω-,∂Ω+={e∈∂Ω:b·n≥0},∂Ω-={e∈∂Ω:b·n<0},J=(0,T](T>0)为时间域，对流系数b∈(w1,∞(Ω))2,b(x)=(b1(x),b2(x))T,u0(x,y)∈L2(Ω)为已知函数.扩散矩阵D=(dij)是正定对称的,满足Lipschitz连续条件，且存在正常数D1,D2使得D1ξTξ≤ξTDξ≤D2ξTξ,∀ξ∈R2.此方程可以刻画流体中的热传导、污染物的扩散等实际问题.

本文根据对流项的特点，提出了迎风间断有限体积元方法，此方法即具有间断有限体积元方法的特点，又具有迎风格式的特点.即高精度，可并行，空间构造简单及保持局部质量守恒等特点，而且有效地避免了锋线前沿的数值弥散现象.笔者给出了问题的迎风间断有限体积元格式，得到了L2模和能量模的误差估计.

1 迎风间断有限体积元格式

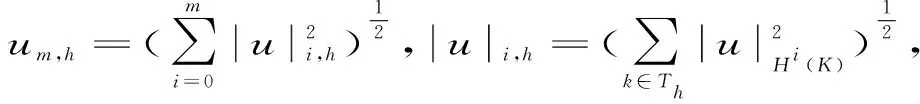
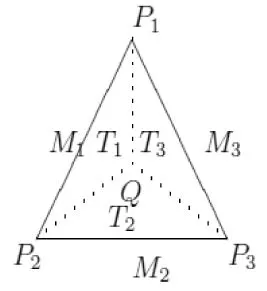
图1 原始剖分与对偶剖分

在原始剖分Th上定义有限维的试探函数空间

Uh={uh∈L2(Ω):uh|k∈P1(K),∀K∈Th},

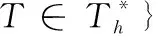
其中Pl表示定义在单元K(T)上的次数小于等于l(l=0,1)的多项式集合.

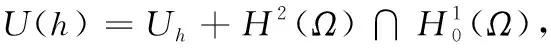
在(1a)式两端同时乘以vh∈Vh,在对偶单元上积分，利用Green公式得

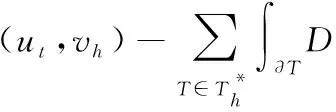
(2)

设e=∂K1∩∂K2,则

根据以上均值以及跃度的定义，显然可以得到下面的结论

(3)

应用上式，并注意到[D▽uh]|e=0,∀e∈Γ0,D▽u·n=0,∀e∈ΓΓ0.所以有

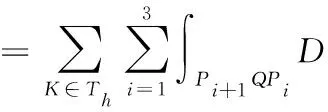
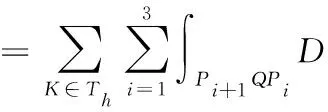
(4)

定义双线性形式

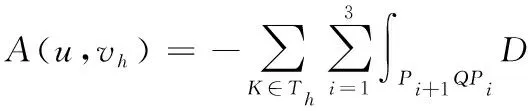
(5)

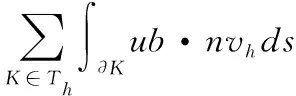
图2 迎风逼近的示意图

设Pi,Pi+1∈Γ0是两个相邻顶点，取对偶剖分的相邻单元Ki,Ki+1，e是Ki,Ki+1的公共边，且e∈Γ0，对于纯量w定义[[w]]|e=w|Ki-w|Ki+1,当e∈∂Ω,则有[[w]]|e=w|e.

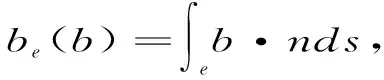
其中Mi为Pi,Pi+1的中点.

于是我们得到问题的半离散迎风间断有限体积元格式为：求uh:[0,T]→Uh使得

(6)

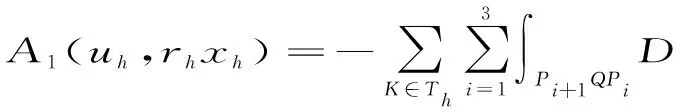
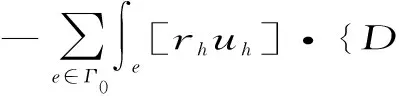
其中惩罚性α的定义同文献[3].由于u是(1)的解，则[rh]|e=0,故(1)的解满足A(u,rhxh)=A1(u,rhxh)

我们采用向后差商的隐式Euler格式,对时间变量进行离散.

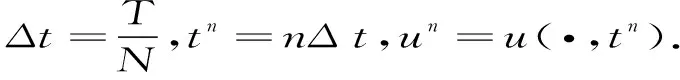
(7)

其中Πhu0为定义的差值投影.

2 一些引理

引理1[3](迹不等式)若e为单元K的具有长度为he的边，则

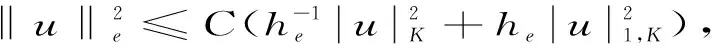
引理3[3]对∀uh,vh∈Uh,存在与h无关的正常数C，使得

引理5[6]对∀uh,vh∈Uh,存在与h无关的正常数C，使得

其中∏hu为定义的关于u的插值投影.

引理6[3]算子γh关于L2内积是自伴的，(uh,γhvh) = (vh,γhuh)，并定义

引理7[3]存在与h无关的正常数C1,C2，使得

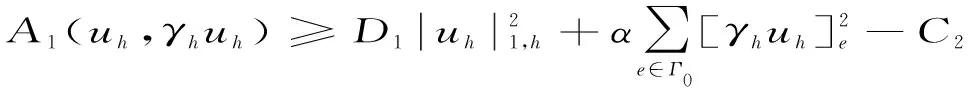
引理8[6]存在与h无关的正常数C，使得

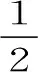
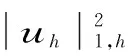
3 误差分析

(8)

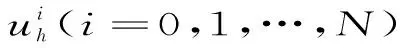
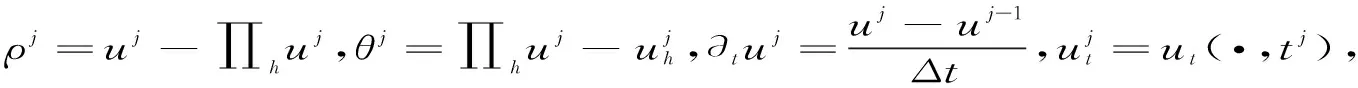
(∂tθj,γhxh)+A1(θj,γhxh)+a(θj,γhxh)+B1(θj,γhxh)

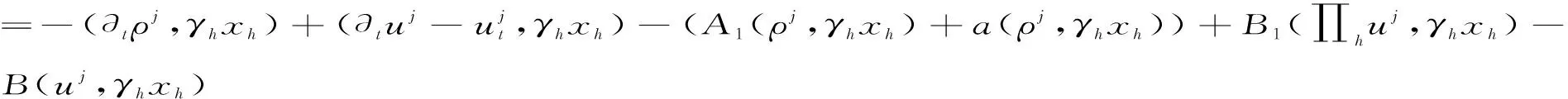
首先对上式左端项进行估计，左端第一项有以下估计

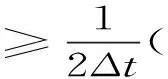
利用引理7和引理9证明左端其余项，有以下估计

下面对(8)右端项逐项进行估计

|J1|≤‖∂tρn‖2+ε‖θj‖2≤Ch4+ε‖θj‖2，

将上述估计式代入，整理可得

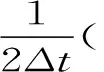
根据范数的定义，取h,ε充分小，α充分大时，对上式两端同乘以2Δt，并对j从1～n求和，整理可得

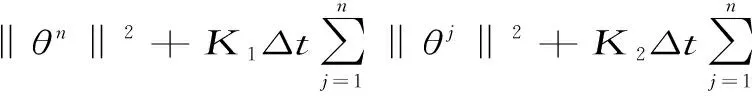
当Δt充分小时，‖θn‖≤C(h+Δt).结合此式与(8)，三角不等式，证得结论.

下面证明H1模误差，在误差方程中取xh=∂tθj,则有

(∂tθj,γh∂tθj)+A1(θj,γh∂tθj)+a(θj,γh∂tθj)+B1(θj,γh∂tθj)

+B1(∏huj,γh∂tθj)-B(uj,γh∂tθj)

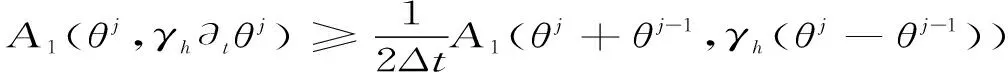
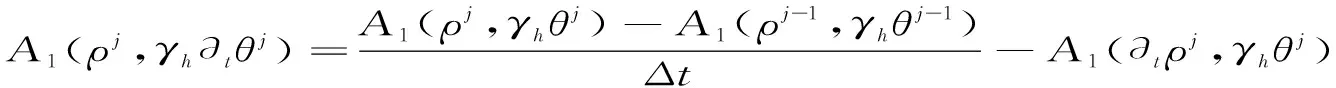
所以可改写为

对上式两端同乘以2Δt，同时对j从1～n求和，可得

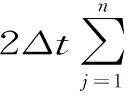
+2B1(∏hun,γhθn)-2B(un,γhθn)=L1+L2+L3+L4+L5+L6+L7+L8+L9+L10

用Cauchy不等式，引理3,4,5,6,8,10及ε不等式，(8)式的右端项的估计如下

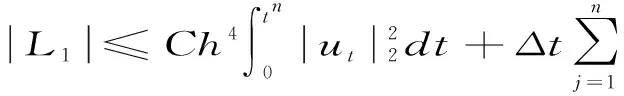
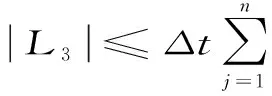
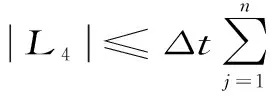
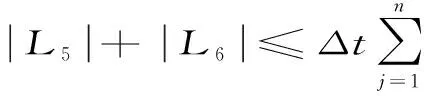
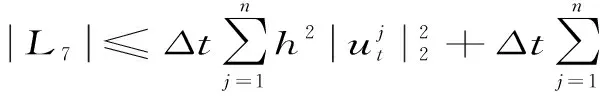
将上式代入，由离散Gronwall不等式

结合(8)以及三角不等式即可证明结论.