北师大版与人教A版高中数学教科书比较研究

【摘 要】 本文比较分析普通高中数学课程标准实验教科书人教A版与北师大版“空间图形的基本关系与公理”这一节内容，揭示两版本教科书所渗透的数学思想方法、数学语言的使用与表达及例习题配置情况，进而为高中立体几何教学提供参考建议.研究发现，两版本教科书内容结构设置类同于《几何原本》的公理化系统，渗透公理化思想方法；内容呈现方式始于公理化思想方法的应用；北师大版图象语言的使用频率高于人教A版，而人教A版同时使用三种语言描述的知识点则多于北师大版；例题均设置了推理论证和三种语言间转换的题目，但习题设置存在差异，各有侧重.最后根据研究结果提出了相应的教学建议.

【关键词】 教科书；比较研究；空间图形的基本关系与公理；教学建议

1 引言

普通高中数学课程标准（2017年版）指出：数学教育帮助学生掌握现代生活和进一步学习所必需的数学知识、技能、思想和方法；提升学生的数学素养，引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界[1].教科书作为依据课程标准和学生接受能力编写的教学材料，它是课程目标与教学内容的具体体现，在一定程度上决定了学生的学习机会和学业成就[2].课标提倡教材编写的多样化，在以课程标准为基础的前提下，不同的教材可以有各自的风格和特点.因此，不同版本教材，对知识内容的安排、数学思想方法的渗透、数学语言的表达也不尽相同，那么不同的数学教科书在渗透数学思想方法、用数学语言进行表达、例习题与内容的匹配等问题的差异就值得研究了.长期以来，几何承担着推理与证明的责任，这种责任并不会因为数学教育的改革而消亡，究其缘由，几何知识比其他数学内容能更好地使学生体会和理解数学世界的推理与证明，或者说是更明确、更符合人们认识事物的直觉[3].因此，本文选取人教A版和北师大版教科书立体几何部分内容进行比较，探析两版本教科书渗透数学思想方法、运用数学语言、例习题与内容的匹配的问题，以期为教材编写者就数学思想方法与知识的有机融合提供数据支撑与理论依据，为一线教师教学提供教学建议与方法.

2 研究方法与内容

本文选取普通高中数学课程标准实验教科书人教A版[4]（以下简称“人教A版”）与普通高中数学课程标准实验教科书北师大版[5]（以下简称“北师大版”）必修2关于“空间图形的基本关系与公理”的內容，比较的具体内容见表1.基于人教A版与北师大版教科书的文本材料，运用文献研究和比较研究的方法，从内容呈现、数学语言及例习题设置三个维度对两版本教科书进行深度剖析.

3 研究结果

3.1 内容呈现

3.1.1 两版本教科书内容结构设置与《几何原本》公理化系统相似，渗透公理化思想方法

内容结构反映了本节教材所包括知识点之间的相互关系，且每一部分内容都是必不可少的，这个有机构成的知识团从侧面反映了它所蕴含的数学思想方法.王仲春先生提出的公理化方法的结构层次分为4层次架构：第一层次——基本概念（对象、基本关系）；第二层次——定义；第三层次——公理组（包括逻辑公理）；第四层次——定理及其证明[6].以此为比较分析框架，两版本教科书内容结构见表2.

从表2可以看出，两版本教科书在“空间图形的基本关系与公理”这一节包含的知识点基本一致，只在定义层次人教A版比北师大版多了空间平面的定义，这是由于两版本教科书在小学和初中两个学段几何内容的安排略有差异.公元前300年欧几里得写成了名著《几何原本》，其对于人类文明的最大贡献在于用演绎方法构建了一个公理化体系，而两版本的教科书内容结构也完全符合公理化方法的层次结构，从公理化体系的角度对几何章节的内容进行安排.基于《原本》的公理化体系，无形中渗透了公理化思想方法，使立体几何章节各部分内容有机结合，呈现出一个精密运作的几何世界.

3.1.2 两版本教科书内容呈现方式“貌离神合”——公理化思想方法的应用

北师大版和人教A版关于空间图形基本关系与公理的呈现方式比较见表3.

从表3可以看出，两版本基于《标准》要求，借助长方体模型，在学生直观认识和理解空间点、线、面的位置关系的条件下，抽象出空间线、面位置关系的定义，同时了解作为推理依据的公理和定理[7].但是，通过比较发现，尽管两版本教科书知识点呈现顺序大相径庭，看似杂乱无章，实则都是按照一定的主线，将各个知识点以逻辑规则和顺序有机结合.人教A版从空间图形与位置关系的视角，分别以平面、空间中直线与直线之间的位置关系、空间中直线与平面之间的位置关系、平面与平面之间的位置关系为小节标题，基于这样的划分分别引出与之相应的知识点，即以空间图形与位置关系为主线引出与之有关联的公理.如：由平面引出公理1、2、3；由空间两条直线位置关系引出公理4.北师大版则选择从公理的角度出发，引出与每条公理密切相关的空间图形位置关系.如：由公理2引出空间直线与平面之间的位置关系等.

由上可知，虽然人教A版和北师大版知识点展开所依据的主线各有侧重，但事实上两版本教科书内容呈现方式貌离神合：教材编写者都应用了公理化思想方法.利用公理化思想方法可以揭示一个数学分支中命题与命题之间的内在关系，从而使它系统化、逻辑化，有利于人们掌握[8].因此，无论选择以位置关系还是公理为主线，都充分运用公理化思想方法，使这一节内容有机结合，使之成为一个有逻辑、有关联的整体.这样的教科书，不管对于教师教学还是学生学习都是一场潜移默化的思维训练.

3.2 数学语言

数学语言是在数学思维中产生和发展的，是数学思维不可缺少的重要工具.数学语言具体可以分为图象语言、文字语言、符号语言三种.数学教材要渗透和传播数学知识与思想方法，就需要使用数学语言来表达.立体几何以空间图形为研究对象，几何内容的学习必然无法缺少数学语言的使用.

3.2.1 北师大版图象语言的使用频率高于人教A版

为了解两版本教科书在图象语言使用方面的区别，本文做出以下对比统计.北师大版“空间图形的位置关系与公理”内容共7页，其中课文中的插图共25幅；习题（包括练习题）共16道，习题的插图共6幅.以上31幅插图中实物图有5幅，其中包括3张照片，剩余都是几何线条图.人教A版这节内容共14页，其中课文的插图共25幅；习题（包括练习题）共34道，习题的插图共有11幅.以上36幅插图中实物图有3幅，其中包括1张照片，其余都是几何线条图.由此得出下面的对比表.

从表4可以发现，两版本教科书对于课文插图、习题插图、实物图和照片等使用频率相差较大，北师大版图象语言整体使用频率高于人教A版.北师大版教科书平均每页分布3.5幅图，而人教A版还不足2幅.平均图题比相差不大，但北师大版仍然高于人教A版.实物图所占率和照片所占率，北师大版是人教A版的2-3倍.

3.2.2 人教A版同时使用三种语言描述的知识点多于北师大版

由图象语言向符号语言的转化需要借助文字语言的中转，文字语言是对图形的描述、解释与讨论，符号语言则是文字语言的简单化和再次抽象.两版本教科书这一节在对位置关系、公理和定理的描述中，既有只使用一种语言的情况，如公理4——空间平行线的传递性，也有同时使用两种或三种语言的情形.事实上，三种语言之间的转换都是为其后的演绎推理做准备，为学生逻辑推理能力的培养添砖加瓦.因此，文本统计了两个版本教科书中使用不同语言的知识点的情况，见表5.

从表5的数据统计可以得出，两版本教科书使用2-3种语言描述知识点的比例更大.北师大版为83.3%，人教A版为84.6%.此外，两版本教科书中使用三种语言表述的知识点是最多的，北师大有7个，占比为58.3%，人教A版有9个，占比为69.2%.很明显，人教A版中三种语言描述的知识点多于北师大版.

3.3 例、习题设置

例、习题是数学教科书的重要组成部分，是巩固数学基础知识、形成数学基本技能、领会数学基本思想、积累数学基本活动经验以及培养学生数学核心素养的主要途径[9].

3.3.1 两版本教科书例题均设置了推理论证和三种语言间转换的题目

这一节内容中，人教A版设置了4道例题，其中3道考查空间点、直线、平面之间的位置关系；1道为推理论证题.北师大版设置了2道例题，1道考查两条直线之间的位置关系，1道为推理论证题.可以发现，两版本教科书不约而同都设置了一道证明题作为例题，均为“证明空间四边形ABCD的边AB，BC，CD，DA的中点E，F，G，H，构成的四边形为平行四边形”这样一道经典题，证明的过程比较简洁，从中位线出发依据公理4即可证明，但这道题却渗透出数学公理化思想方法，让学生在会做例题的基础之上体会知识点之间的逻辑关系和公理化体系，并训练学生养成严密的逻辑思维.除此之外，人教A版的4道例题和北师大版的2道例题均注重考察三种语言之间的转换，每道例题都配以相应的图形，同时文字语言和符号语言的表述并重.人教A版的例1特意设置为将图象语言转换为符号语言的练习，这也弥补了课文中未设置这样内容的缺憾.

3.3.2 两版本教科书习题设置存在差异，各有侧重

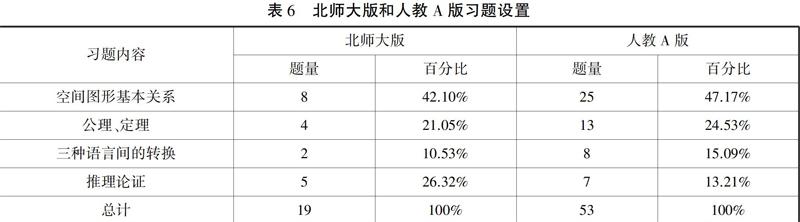
研究拟从习题内容题量分布及对应的百分比两个维度对两版本教科书的习题配置进行比较分析.将本节习题分为空间图形基本关系、公理定理、三种语言间的转换、推理论证这四类.其中将与“异面直线及其夹角”有关的题归类至“空间图形基本关系”这一组；“三种语言间的转换”指考查有关三种数学语言的描述转化的问题；“推理论证”指涉及到有关演绎推理的题目.具体统计结果见表6.

从表6可以看出，无论是北师大版还是人教A版教科书，在习题的配置中，均着重“空间图形基本关系”和“公理、定理”这两类习题，为学生巩固本节内容所学知识提供了平台，这也符合教科书的习题设置的要求.但通过比较可以发现，两版本教科书关于“三种语言间的转换”和“推理论证”的题目的设置存在明显差异，而且各有侧重.北师大版的两类题目数量占到总题数的36.85%，其中“推理论证”类题目的数量甚至超过“公理、定理”类题目，百分比达到26.32%.而人教A版这两类题目数量占总题数的28.30%，相比北师大版低.其中“三种语言间的转换”类题目数量更多一点，百分比达到了15.09%.但从总题数来看，人教A版习题数量是北师大版的两倍多.

4 研究结论及建议

4.1 结论

4.1.1從宏观视角看，北师大版与人教A版教科书都渗透了公理化思想方法

欧几里得《几何原本》是有史以来用公理化思想方法建立起来的第一门演绎数学，而且成为以后很长时期严格证明的典范

[10].两版本教科书在内容选取上符合公理化方法结构层次，以空间图形、关系、公理和推理论证为结构基础，与《几何原本》相似.关于内容呈现方式，运用公理化思想方法将本节知识点逻辑、关联、有机地串联起来，建立本节内容的“公理系统”.除此之外，两版本教科书都配置了相应比例的推理论证题目，在应用层面渗透公理化思想方法.

4.1.2 从微观视角看，北师大版和人教A版对于数学语言及例习题配置的侧重各有不同

两版本教科书均十分重视学生对数学语言的学习，但北师大版偏重图象语言的内容设置.图象语言是将现实事物进行数学抽象的第一步，也是问题解决的第一水平[11]，更能培养学生直观想象的能力.但人教A版则更注重三种数学语言转换的学习，从表5、6及例题配置可以看到，人教A版在相关内容所占比例均比北师大版高，此外，人教A版在例题中专门设置了一道三种语言相互转换的题目，北师大版与之相比则显得比较欠缺.例习题的配置中，北师大版有关推理论证题目占总题数的比例均比人教A版高，除此之外，北师大版题目多注重应用.因此，人教A版侧重为后续定理及推理论证的学习奠定基础，而北师大版更关注学生在知识应用过程中加深对其的理解.

4.2 建议

4.2.1 立体几何课堂教学应重视公理化思想方法的渗透

公理化思想方法在数学教学和学习中具有重要的作用和意义.首先，公理化思想方法可以揭示一个数学系统或分支的内在规律性，从而使它系统化、逻辑化，有利于人们学习和掌握.其次，由于公理系统是一个逻辑演绎系统，所以对培养学生的逻辑思维能力和演绎推理能力都有其重要意义[12].虽然《标准》中突出直觀感知、操作确认、归纳类比等方法，但演绎推理仍然是验证猜想、证明结论的重要手段.因此，教师作为知识传递的源头，应在充分理解公理化思想方法的基础之上，将其融入自己的课堂教学中，向学生展示公理化思想方法及系统的特点与优势，在构建学生知识体系的过程中沉淀数学思想方法.

4.2.2 立体几何教学中合情推理与演绎推理应相辅相成

数学推理位于数学核心素养体系塔的第三层次——数学思维层，包括演绎推理和合情推理.合情推理作为获得猜想、发现结论的重要方式，有助于培养学生学生大胆猜想、勇于创造的探索精神；演绎推理注重运用事实和逻辑进行论证，有助于个体形成尊重事实和证据的理性精神[13].因此，立体几何角教学中教师应该在借助几何直观、空间想象、操作确认、度量计算等手段的基础之上，不失时机的引导学生进行抽象概括，体会公理化思想方法，发展学生必要的论证思维水平.

4.2.3 教师应充分利用两版本教材，取长补短，设计优质教案

教师在讲授这一部分内容时，应同时参考这两个版本的教科书（甚至是多个版本），取长补短，精心设计.北师大版更注重知识的应用性，而人教A版则以夯实学生基础为主.两个版本各有特色，教师在进行新授课之前应仔细研读这两版本教科书，基于学生学情制定相匹配的教学目标，选择合适的教学内容，创设与之相适应的教学情境，最终进行教学.因材施教，一标多本即是追求个性化教学，因此教师不应仅仅局限于某一个版本的课本.

参考文献

[1] 中华人民共和国教育部. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社， 2017.

[2] 贾随军， 吕世虎， 张定强，等. 普通高中数学课程标准实验教科书人教A版与北师大版的比较研究——以“函数及其表示”为例[J]. 数学教育学报， 2014， 23（5）：46-50.

[3] 王建明， 张思明， 王鹏远，等. 高中几何课程标准之我见[J]. 数学教育学报， 2001， 10（4）：55-58.

[4] 人民教育出版社. 普通高中课程标准实验教科书数学2必修（A版）[M]. 北京：人民教育出版社， 2014.

[5] 北京师范大学出版社. 普通高中课程标准实验教科书数学必修2[M]北京：北京师范大学出版社，2014.

[6] [8]王仲春， 李元中， 纪善韬. 数学中的公理化方法[J]. 西北师范大学学报（自然科学版）， 1987（2）：87-91.

[7] 中华人民共和国教育部制订. 普通高中数学课程标准（实验）[M]. 北京：人民教育出版社， 2003.

[9] 汪飞飞. 基于数学认知水平的两岸高中数学教科书习题比较——以“指数和对数函数”为例[J]. 中学数学， 2017（15）：12-16.

[10] [12]王仲春. 数学思维与数学方法论[M]. 北京：高等教育出版社， 1989.

[11] 田载今. 充分发挥三种数学语言的功能——对新编高中数学教科书中“直线、平面、简单几何体”一章的一些想法[J]. 课程·教材·教法， 1998（2）：20-23.

[13] 吕世虎， 吴振英. 数学核心素养的内涵及其体系构建[J]. 课程·教材·教法， 2017（9）：12-17.

作者简介

刘冰（1993—），女，甘肃庆阳人，西北师范大学教育学院研究生.