一种求解作业车间调度问题的改进遗传算法

（长安大学 道路施工技术与装备教育部重点实验室，西安 710064）

0 引言

作业车间调度问题（Job Shop Scheduling Problem，JSP）是一类典型的组合优化问题，科学、合理的调度方案能够有效提高生产效率、降低加工成本，而问题的求解方法则是实现这些目标的重要保证。遗传算法（Genetic Algorithm，GA）作为一种群智能算法，具有隐式并行性和全局搜索特性[1～3]，是求解作业车间调度问题的有力工具，但标准遗传算法存在早熟收敛、解的稳定性差、遗传参数难以确定等诸多缺点[4,5]。

本文针对标准遗传算法的不足之处对其作了相应的改进，提出了一种新的个体适应度值计算方法，采用三种方式对染色体进行配对交叉以增强个体的多样性，在选择阶段引入了精英保留策略[6]来确保算法的收敛性，在迭代过程中使算法自动对交叉和变异概率进行动态调整，并讨论了动态概率调整函数中的参数取不同值时算法性能的变化情况。

1 JSP问题的数学模型

JSP问题的一般性描述为：n个工件在m台机器上加工，工件每道工序的加工机器和加工时间确定，同时满足以下约束条件：1）每个工件的工序按其工艺路线顺次加工，中途不得中断；2）同一时刻，一道工序只能在一台机器上加工；3）同一时刻，一台机器只能加工一道工序，4）每个工件在每台机器上只加工一次。所要解决的问题是对各工件的加工顺序进行合理安排以优化一个或多个加工性能指标。

本文以最小化最大完工时间为优化目标，假设安装与调整时间包含在工序的加工时间内，各工件无加工优先级之分，相应的数学模型如下：

优化目标：

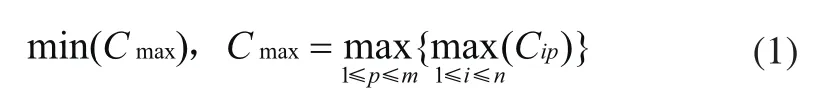
约束条件：

式(1)为优化目标函数；式(2)表示工序约束；式(3)表示机器约束；式(4)表示工件完工时间大于零；式(5)表示各下标变量的取值范围。

式中，Cmax为最大完工时间；Cip为工件i在机器p上的完工时间；m为机器总数；n为工件总数；Sip为工件i在机器p上的开工时间；M是一个极大的正数；i, j为工件编号；p，q为机器编号。

2 算法设计

2.1 染色体编码

本文采用基于工序的实数编码来表示个体（染色体）[7]，一组编码代表一种可行的加工方案，如对于工序码[3 2 1 1 2 3 2 3 1]，各个数字代表被加工件的工件号，数字第几次出现就代表相应工件的第几道工序，如第一个“3”表示三号工件的第一道工序，第二个“3”表示三号工件的第二道工序。

2.2 种群初始化

初始种群用于生成第一代子代个体，本文采用随机方式生成初始种群，利用MATLAB软件自带的随机排序函数“randperm”随机打乱一组染色体的编码，通过多次调用该函数来获得所需规模的初始种群。

2.3 计算个体适应度值

在以最小化最大完工时间为优化目标时，以往的研究大多以目标函数值的倒数作为个体的适应度值，这种方式所求得的个体的适应度值均较为接近，难以体现出个体差异，从而不利于在选择阶段将具有不同适应度值的个体有效区分开来。因此，对适应度函数进行改进以拉开个体间的差距，并采用精英保留策略使最优个体存活下来不受遗传操作的破坏而直接遗传到下一代。

设Ms(i)表示个体i对应的最大完工时间，Max和Min分别表示种群中的最大值与最小值，定义个体的适应度函数为：

假设有5个个体，对应的最大完工时间依次为：[10, 11, 12, 13, 14]，按传统方法算得的个体适应度值分别为：[0.1, 0.0909, 0.0833, 0.0769, 0.0714]，个体的选择概率如图1(a)所示；按式(6)算得的个体适应度值为：[1, 0.6818, 0.4161, 0.1923, 0]，对应的个体选择概率如图1(b)所示。

对比图1(a)和图1(b)可以看出，传统的适应度值计算法中，每个个体几乎占据了相同的扇形面积，即所有个体将以近似相等的概率被选中，而改进的适应度值计算方法中，个体之间则具有较高的区分度，能够保证适应度值最低的个体（如个体5）在选择阶段被淘汰，而适应度值高的个体以较大的概率被复制，从而在真正意义上体现出了遗传算法“优胜劣汰”的特点。

2.4 选择算子

采用轮盘赌法[8,9]选择个体，计算公式如下：

图1 个体的选择概率

式中，sum(f)表示个体适应度值之和，p(i)表示个体i被选择的概率，q(i)为个体i的累计概率，产生一个取值在区间[0,1]内的随机数δ，若δ≤q(1)，则选中第1个个体，否则的话，若q(i-1)＜δ≤q(i)，则选中第i个个体。

2.5 交叉与变异算子

2.5.1 交叉与变异方式

本文采用优先工序交叉法（Precedence Operation Crossover，POX）进行交叉操作[10]，并对其进行了扩展。标准POX法中，首先随机产生两个基序列J1、J2，将配对的父代个体P1、P2所含的J1中的基因按原位复制到子代个体C1、C2中，而将所含的J2中的基因按原有顺序依次填入到子代个体C2、C1的空位基因处[11]，从而得到交叉后的子代个体C1和C2。

POX法的第一种扩展方式为：将父代个体P1、P2所含的J2中的基因逆序后再填入到子代个体C2、C1中；第二种扩展方式为：将父代个体P1、P2所含的J2中的基因随机打乱顺序后再填入到子代个体C2、C1中。两种改进的POX法中，父代个体所含的J1中的基因的处理方式与标准POX法相同。迭代时随机选择基本POX法与改进的POX其中的一种交叉方式，从而以多种方式使子代继承父代的优良基因，提高了子代个体的多样性。

变异属于小概率事件，但有利于扩大种群的多样性，本文采用互换法（Reciprocal Exchange Mutation，REM）进行变异操作[12]，即随机选择两个含有不同基因的基因位，将对应元素调换位置。

2.5.2 交叉与变异概率

标准遗传算法以固定的交叉概率和变异概率进行相应的操作，当二者取值较小时会使搜索范围变小，不利于寻找到更优解，而取值较大时则可能导致已有的优良个体在交叉和变异操作后变得更差。因此，本文设计了一种动态自适应交叉概率和变异概率，一方面根据个体在种群中的较高或较低的地位（适应度值越大，地位越高，反之则越低）来给予其较小或较大的交叉与变异概率，另一方面通过动态概率调整函数使迭代初期个体以较大的概率进行交叉和变异，以扩大寻优范围，避免算法早熟收敛，而在迭代后期则减小交叉与变异概率，以降低前期所得到的优秀个体被交叉和变异操作所破坏的概率，同时保证算法尽快收敛。

改进后的动态自适应交叉概率和变异概率的计算公式如下：

式中，i为当前迭代次数，N为终止迭代次数，指数v是调整参数，取值为区间[1,5]内的整数，Pc为交叉概率，Pm为变异概率，kc, km分别为区间[0,1]内的常数，fc为两个交叉个体的较大的适应度值，fm为变异个体的适应度值，fa和fmax分别为当前种群的平均适应度值和最大适应度值。

式(9)中，指数v取不同值时，得到的动态概率调整函数cos(u)的图形如图1所示。

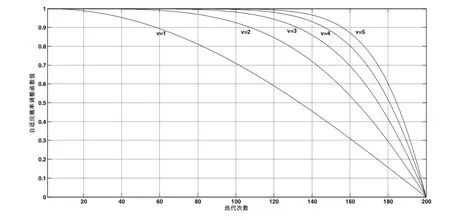
图2 动态概率调整函数图形

从图中可以看出，随着迭代次数增加，函数cos(u)的值从1变为0，斜率逐渐增大，从而在迭代初期保持较大的Pc和Pm进行寻优，在迭代后期则以较小Pc和Pm来加速收敛，而指数v取值越大时，曲线凸起程度越大，从而在越多的迭代次数范围内以大概率进行交叉与变异，以扩大种群多样性来搜索更优解，但同时也会使收敛速度降低。因此，当要求算法具有更强的寻优能力时，应取较大的v值，当要求算法具有更快的收敛速度时，应取较小的v值。

改进遗传算法的流程图如图3所示。

图3 改进遗传算法计算过程

3 实例验证

以Ft06基准算例[13]来验证改进后的遗传算法的性能，试验数据如表1所示，程序运行平台为Windows7操作系统下的MATLAB软件，取种群规模为PS=40，迭代次数为FC=200，标准遗传算法采用基本POX法进行交叉操作，采用互换法进行变异操作，交叉和变异概率分别为Pc=0.7，Pm=0.1，改进遗传算法由式(6)计算个体适应度值，随机选择三种交叉方式中的一种进行交叉操作，变异操作仍采用互换变异法，交叉概率Pc和变异概率Pm分别由式(10)和式(11)确定，式中，取kc=0.9，km=0.12，指数v分别取1、2、3、4、5，将标准遗传算法和指数v的不同取值下的改进遗传算法各运行20次，所得结果如表2所示。

表1 各工序加工机器（加工时间）

由表2可知，标准遗传算法求得的最优解为56，而改进遗传算法求得的最优解为55，且后者最优解的个数远大于前者，虽然在v=4，5时，改进算法的平均迭代次数大于标准遗传算法，但无论指数v取何值，改进遗传算法所求目标函数的平均值均小于标准遗传算法对应的值。可见，在最优解的质量和数量上，改进遗传算法均优于标准遗传算法，表明了改进后的遗传算法的有效性与可行性，标准遗传算法与改进遗传算法所求最优解的调度甘特图如图4、图5所示。

表2 改进前/后算法试验结果对比

根据表2数据，得到改进遗传算法中指数v分别取1，2，3，4，5时的目标函数均值与平均迭代次数的变化趋势如图6所示。

由图6可以看出，在改进遗传算法中，参数v的取值与问题解的优度呈正相关关系，而与收敛速度呈负相关关系，与理论分析结果是吻合的，因此，本文所提出的改进遗传算法中，较大的v值有利于提高解的优度，较小的v值有利于提高算法的收敛速度，在实际应用时可根据具体要求来合理选取参数v的值。

图4 标准遗传算法最优解调度甘特图

图5 改进遗传算法最优解调度甘特图

图6 不同v值下的改进遗传算法所求目标函数均值与平均迭代次数变化趋势

4 结束语

本文针对以最小化最大完工时间为优化目标的作业车间调度问题，从个体适应度函数、染色体交叉方式以及交叉与变异概率三方面对标准遗传算法进行了相应的改进，所设计的动态交叉概率与变异概率能够根据个体的适应度值与算法迭代次数而自动调整，从而扩大迭代初期的搜索范围，使算法在前期具有较强的寻优能力，而在后期以较小的交叉与变异概率使算法尽快收敛，同时，对动态概率调整函数的参数v取不同值时算法的性能进行了分析，为实际应用中v值的选取提供了参考。今后的研究可以从种群的初始化方式、个体的选择规则以及遗传算法与其他智能算法的融合等方面入手，从而使求解作业车间调度问题的算法变得更加高效和完善。