杆系结构的大变形几何非线性分析

孟阳君，张家生



杆系结构的大变形几何非线性分析

孟阳君1，张家生2

(1. 湖南文理学院 土木建筑工程学院，湖南 常德 415000；2. 中南大学 土木工程学院，湖南 长沙 410075)

传统的几何非线性分析方法—完全的拉格朗日列式法(TL)、更新的拉格朗日列式法(UL)不适用于大变形几何非线性分析。基于CR列式法的基本原理，整理分析得到平面杆系单元的切线刚度矩阵。根据几何非线性程序编制的关键在于确定大变形条件下的刚性位移和变形位移，据此分析并提出坐标转换矩阵的具体表达式。给出几何非线性分析程序框图，编制几何非线性分析程序PMGXFXX。结合大挠度及大转角算例，对比理论解析解，PMGXFXX程序解最大误差均在5%以内。

几何非线性；CR列式法；大挠度；大转角；程序

结构动力可靠度分析的对象都是处于各种极限状态下的结构，在这些极限状态下结构一般很难保持线弹性，这时考虑结构的非线性因素成为必然。本文仅对结构的几何非线性问题——大挠度及大转角进行探讨。传统的几何非线性分析方法是基于Langrangian坐标系的TL和UL列式法，在几何非线性分析计算中，经常忽略考虑变形后的坐标转换矩阵，导致在大转角问题分析中无法收敛甚至出错[1−3]。TL列式法中，由于局部坐标系变形前后保持不变，未能考虑变形之后结构状态的影响[4]；UL列式法中，单元两端节点按照局部坐标系与整体坐标系之间的Euler角度进行变换，导致单元两端的坐标转换矩阵不同，同时也不能考虑单元弯曲变形的影响[5]。基于上述原因，本文采用CR列式法对几何非线性问题进行分析，并编制相应的分析程序，结合算例进行验证。

1 几何非线性分析(CR列式法)

以平面杆系结构分析为例。考虑图示1(a)梁元，以表示节点在坐标方向的位移，以表示节点在坐标方向的位移，以表示节点逆时针方向的转角。设单元左节点1发生总位移1，1和1，单元右节点2发生总位移2，2和2。变形之后，单元移动到新位置，如图1(b)所示，其位移包含了刚体位移和变形，扣除刚体位移部分后，可算出杆在和坐标方向上方的新的投影长度x和y，单元长度，单元斜率，见式(1)。

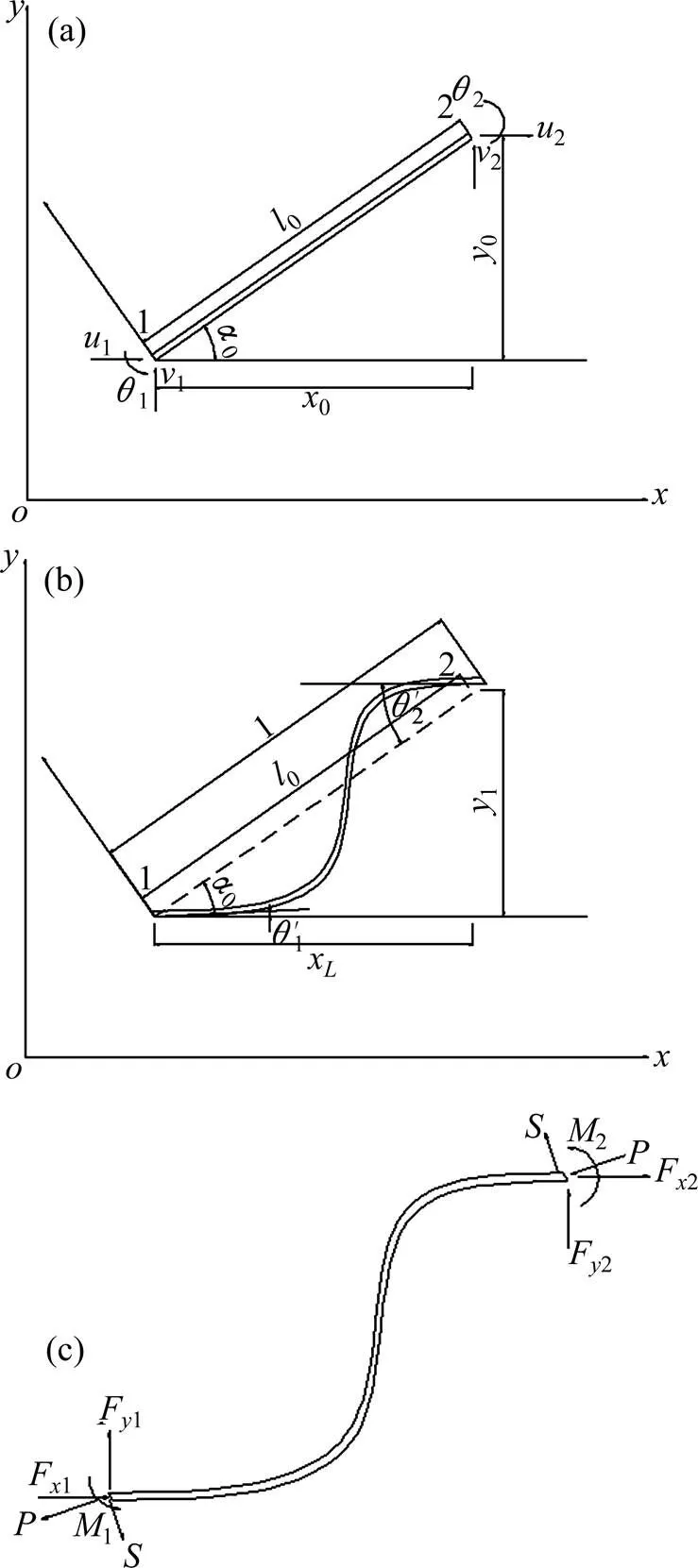
(a) 变形前状态；(b) 变形后状态；(c) 节点力

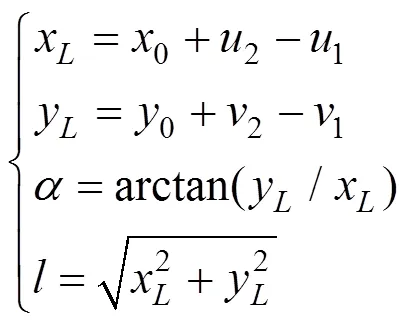
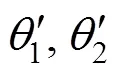
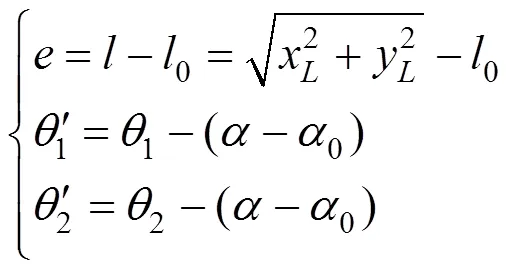
式中：0为单元初始长度；0为单元初始转角。

整理分析得到总体坐标系下梁单元的切线刚度矩阵，见式(3)[6−7]。

式中：

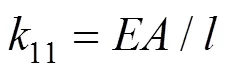
2 几何非线性程序编制

根据CR列式法，采用fortran语言编制平面杆系几何非线性分析程序PMGXFXX。由于杆系内各单元的局部坐标方向各不相同，在进行结构分析时，需要建立统一的总体坐标系。编制PMGXFXX程序关键是坐标转换矩阵的确定。确定坐标转换矩阵首先是确定单元节点发生总位移1，11，2，2和2，这需要依据上一步的分析结果与节点约束情况综合确定，其次是0的确定。计算原理如下：

根据单元变形前后两端节点的坐标位移量，单元初始斜率0的具体表达式见式(4)。

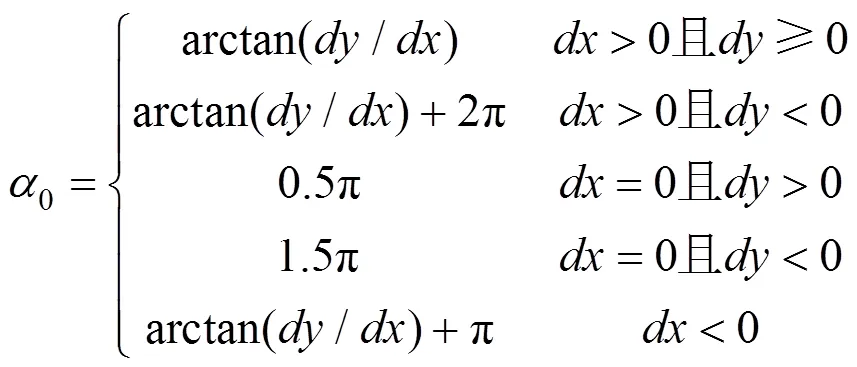
结合单元变形前后两端节点的坐标位移量，单元斜率的具体表达式见式(5)。

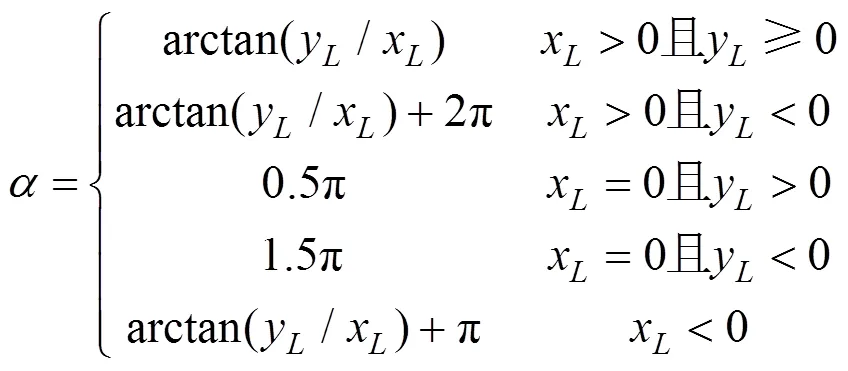
考虑刚性位移及变形位移转角的计算。

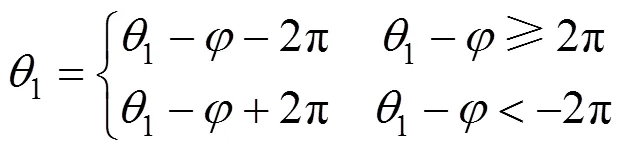
根据刚性位移及变形位移转角的判断与确定。

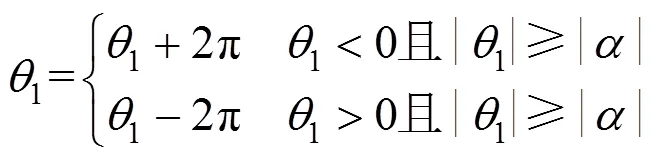
具体坐标转换关系见式(6)。

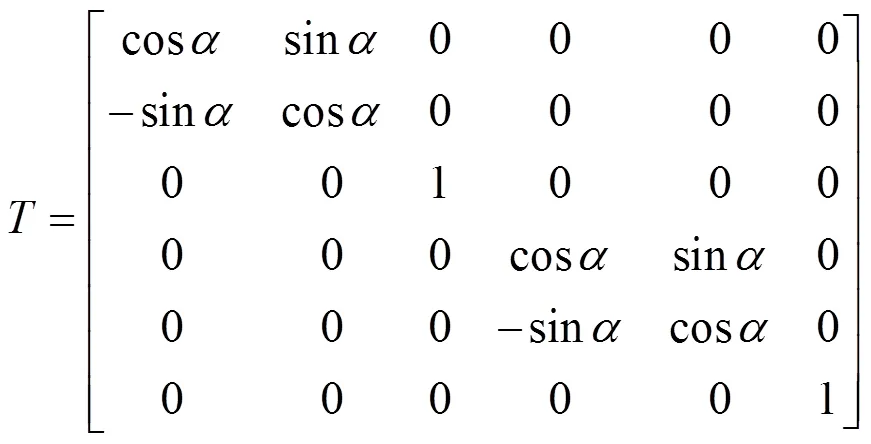
平面几何非线性分析程序PMGXFXX框图见图2。

3 非线性分析算例

3.1 端部受集中力的悬臂梁

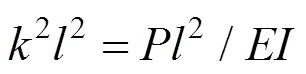
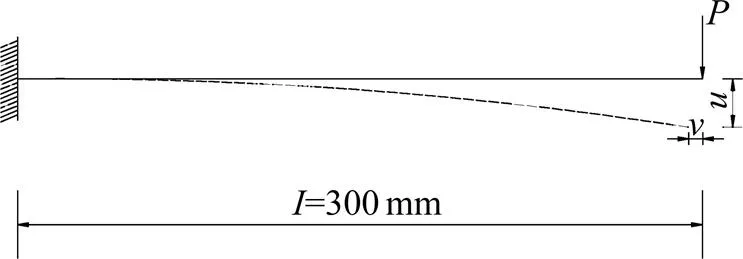
图3 端部受集中力P作用的悬臂梁结构

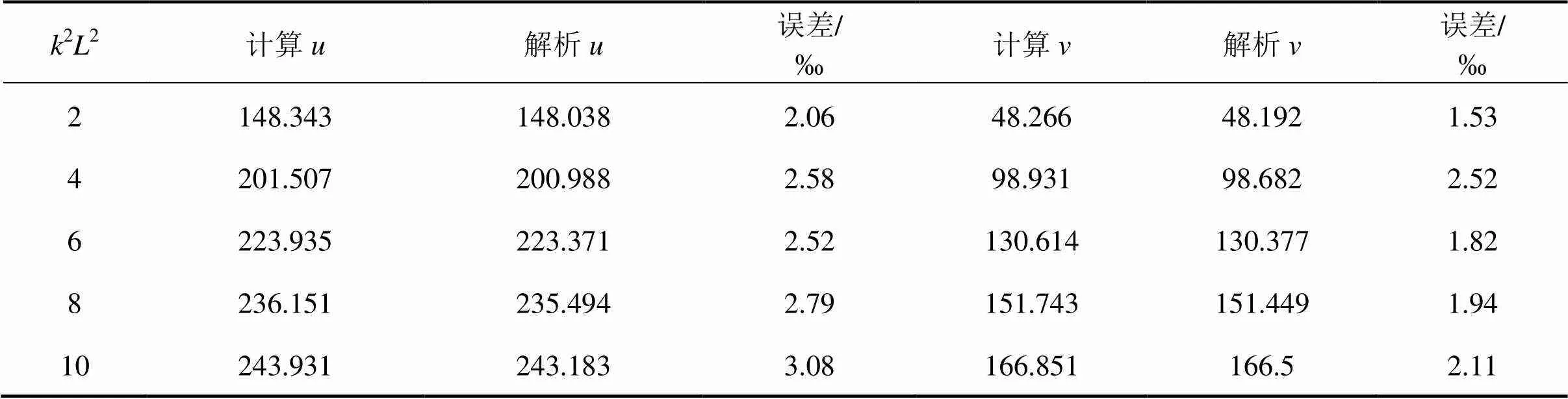
表1 PMGXFXX程序解结果与理论解的比较

3.2 端部受集中弯矩的悬臂梁

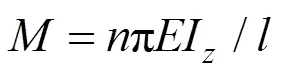
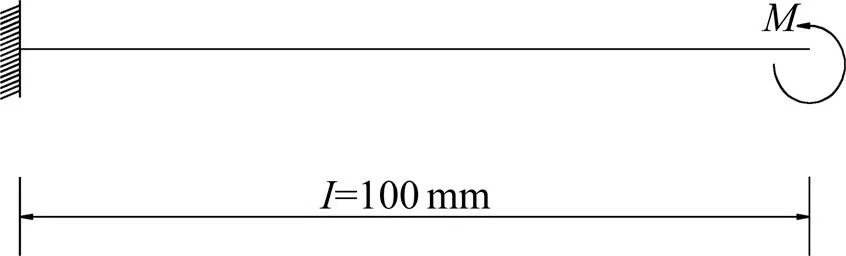
图4 端部受弯矩M作用的悬臂梁结构

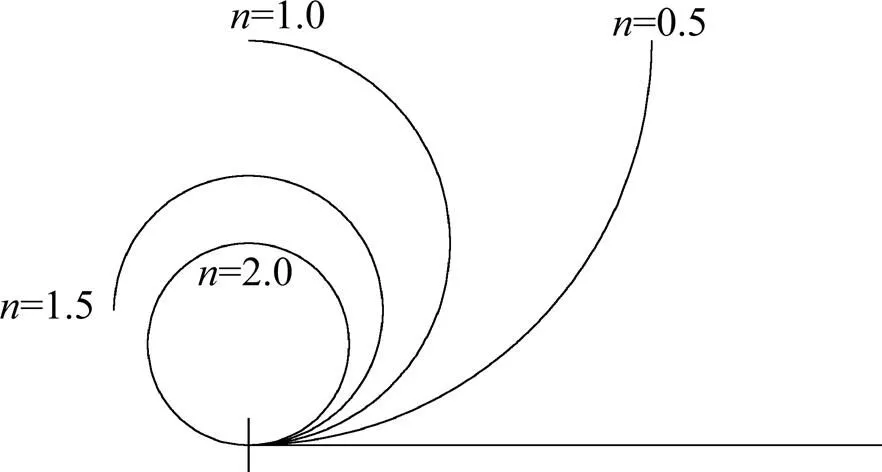
图5 悬臂梁受集中弯矩的变形示意图

3.3 压杆的大挠度分析

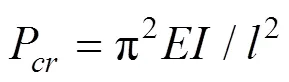
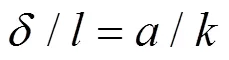
(8)

3.4 桁架的大挠度分析

图7所示桁架结构，横截面面积=4 cm2，弹性模量=200 GPa，跨中受荷载作用(处于线弹性工作阶段)，跨中节点挠度计算结果见表3[12−13]。

3.5 杆系系统的大挠度分析

图8所示杆系结构，所有梁截面尺寸均为0.76 m×1.22 m，所有杆截面尺寸均为0.76 m×0.76 m，弹性模量=20.69 GPa，顶部受集中力作用，顶部节点挠度计算结果见表4。

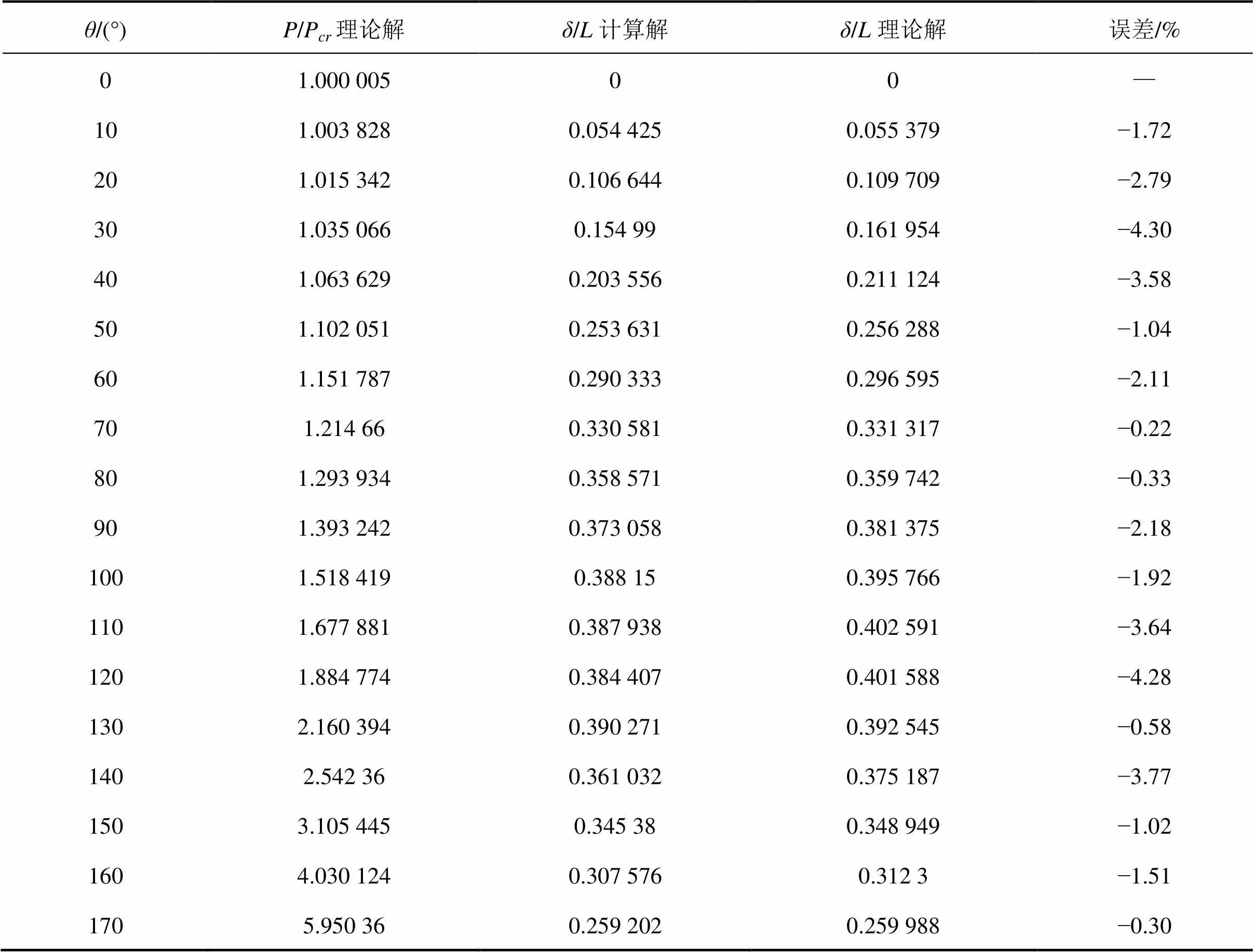
表2 PMGXFXX程序解与理论结果的比较

图7 计算结构模型

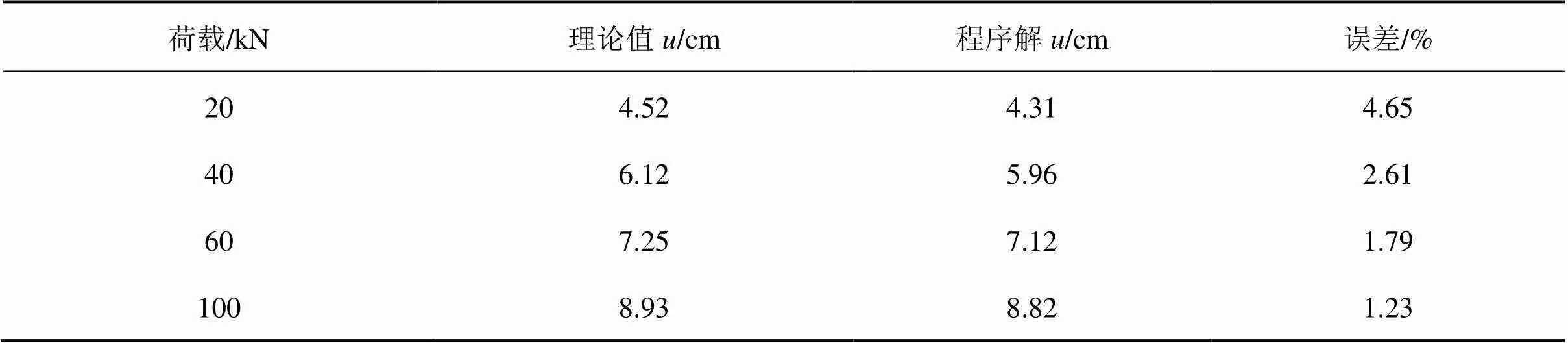
表3 PMGXFXX程序解与理论解的比较

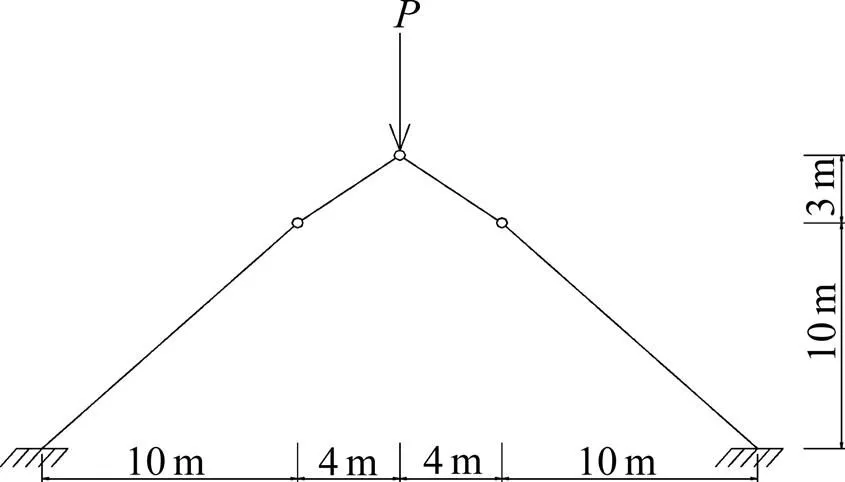
图8 计算结构模型

表4 PMGXFXX程序解与理论解的比较

4 结论

1) 基于CR列式法得到的切线刚度矩阵包含了大挠度、大转角的刚性位移及变形位移信息，提出了坐标转换矩阵的具体表达式，既适用于普通梁单元，也适用于随机场梁单元。

2) 编制几何非线性分析程序PMGXFXX，针对几种不同类别的几何非线性算例进行了对比分析。分析结果如下：端部受集中力的悬臂梁算例(大挠度)，对比解析解，最大误差为3.08‰；端部受集中弯矩的悬臂梁(大转角)，对比解析解，最大误差为2.0‰；压杆的大挠度分析，对比解析解，最大误差为4.28%；桁架的大挠度分析，对比解析解，最大误差为4.65%；杆系系统的大挠度分析，对比解析解，最大误差为3.11%；上述分析结果最大误差均小于5%，满足工程精度要求，同时验证程序的可靠性。

3) 通过算例分析对比表明，几何非线性分析程序PMGXFXX适用于大挠度和大转角的问题分析。

[1] 吴庆雄, 陈宝春, 韦建刚. 三维杆系结构的几何非线性有限元分析[J]. 工程力学. 2007, 24(12): 19−24. WU Qingxiong, CHEN Baochun, WEI Jiangang. A geometric nonlinear finite element analysis for 3D framed structures[J]. Engineering Mechanics, 2007, 24(12): 19− 24.

[2] 叶康生, 陆天天, 袁驷. 结构几何非线性分析中分叉失稳的直接求解[J]. 工程力学, 2011, 28(8): 1−8. YE Kangsheng, LU Tiantian, YUAN Si. A direct method for the computation of bifurcation buckling in geometric nonlinear analysis of structures[J]. Engineering Mechanics, 2011, 28(8): 1−8.

[3] 袁驷, 刘学林, 叶康生. 张拉膜结构极小曲面找形的有限元线法求解[J]. 土木工程学报, 2010, 43(11): 1−7. YUAN Si, LIU Xuelin, YE Kangsheng. FEMOL solution for minimal surface forrn finding of tensile manbrane structures[J]. China Civil Engineering Journal. 2010, 43(11): 1−7.

[4] 马玉全. 改进CR列式法及在几何非线性分析中的应用[J]. 科学技术与工程, 2010, 10(30): 7488−7490. MA Yuquan. A new CR formulation and its application in gecmetrically nonlinear analysis[J]. Science Technology and Engineering, 2010, 10(30): 7488−7490.

[5] Fujii F, Okazawa S. Pinpointing bifurcation points and branch-switching[J]. Journal of Engineering Mechanics, ASCE, 1997, 20(97): 11−17.

[6] YUAN Si, XING Qinyan, WANG Xu, et al. Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super-convergence order[J]. Applied Mathematics and Mechanics, 2008, 29(5): 533−542.

[7] 袁驷, 邢沁妍, 王旭, 等. 基于最佳超收敛阶EEP法的一维有限元自适应求解[J]. 应用数学和力学, 2008, 29(5): 533−542. YUAN Si, XING Qinyan, WANG Xu, et al. Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super-convergence order[J]. Applied Mathematics and Mechanics, 2008, 29(5): 533− 542.

[8] 宋振森, 沈祖炎, 罗永峰. 求解预定位移水平的改进弧长法[J]. 计算力学学报, 2007, 24(4): 509−512. SONG Zhensen, SHEN Zuyan, LUO Yongfeng. An improved arc-length method for searching pre-defined displacement in nonlinear analysis of structures[J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 509−512.

[9] 孟阳君. 大跨径拱桥仿真分析[D]. 长沙: 湖南大学, 2007: 20−35. MENG Yangjun. Simulation analysis of long span arch bridges[D]. Chansha: Hunan University, 2007: 20−35.

[10] Shi J, Crisfield M A. A semi-direct approach for the computation of singular points[J]. Computers and Structures, 1994, 11(8): 100−106.

[11] Hashash Y M A, Hook J J, Schmidt B, et al. Seismic design and analysis of underground structures[J]. Tunnelling and Underground Space Technology, 2001, 16(4): 247−293.

[12] Teh L H, Clarke M J. Symmetry of tangent stiffness matrices of 3D elastic frame[J]. Journal of Engineering, 1999, 8(3): 28−34.

[13] YUAN S, YE K, Williams F W, et al. Recursive second order convergence method for natural frequencies and modes when using dynamic stiffness matrices[J]. International Journal for Numerical Methods in Engineering, 2003, 15(8): 37−42.

(编辑 阳丽霞)

A large deformation geometric nonlinear analysis for frame structure

MENG Yangjun1, ZHANG Jiasheng2

(1. School of Civil Engineering and Architecture, Hunan University of Arts and Science, Changde 415000, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

Traditional geometric nonlinear analysis methods of TL and UL method are not suitable for large deformation geometric nonlinear analysis. Based on a basic principle of CR formulation, a plane beam element tangent stiffness matrix was derived. According to the key of geometric nonlinear programming which includes determination of rigid displacement and deformation displacement, a coordinate transformation matrix was analyzed and its concrete expression was derived. A geometric nonlinear analysis program chart was given and a geometric nonlinear analysis program-PMGXFXX was compiled. Combined with large deflection calculation examples and large angle calculation examples, the maximum error of PMGXFXX solutions was found to be within 5% by comparing with the theoretical analytical solution.

geometric nonlinear; CR formulation; large deflection; large angle; program

10.19713/j.cnki.43−1423/u.2018.08.017

TU323

A

1672 − 7029(2018)08 − 2034 − 06

2017−05−20

国家自然科学基金资助项目(50978258)；湖南省教育厅一般项目(16C1091)

孟阳君(1982−)，男，湖南澧县人，高级工程师，博士，从事大跨桥梁结构理论研究；E−mail：352357749@qq.com