非线性破坏准则下浅埋隧道支护参数上限解

张佳华，张标

非线性破坏准则下浅埋隧道支护参数上限解

张佳华1, 2，张标3

(1. 湖南科技大学 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室，湖南 湘潭 411201；2. 湖南科技大学 煤矿安全开采技术湖南省重点实验室，湖南 湘潭 411201；3. 中南大学 土木工程学院，湖南 长沙 410075)

鉴于土体材料破坏准则的非线性以及参数离散的自然属性，针对浅埋隧道的稳定性问题，提出基于极限分析非线性理论的可靠度计算方法。研究结果表明：将非线性破坏准则退化成线性破坏准则后，本文计算结果与已有研究成果基本一致，验证了文中方法的正确性。在上限解分析中，土体的非线性系数对围岩压力以及破坏范围有很大影响，建议进行支护设计时必须考虑土体破坏准则的非线性，防止因支护力过小或安全系数不足而引发坍塌事故。在可靠度计算中，非线性系数是影响隧道结构可靠度的主要因素，针对非线性系数给出了浅埋隧道满足3种安全等级所需要的安全系数与支护力，为隧道设计规范进行了补充，也为今后浅埋隧道的支护设计提供了参考价值。

浅埋隧道；非线性破坏准则；极限分析；可靠度；安全系数；支护力

由于埋深较浅、自稳能力较差，浅埋隧道在开挖过程中经常会发生坍塌事故，这给施工人员的生命以及财产带来了极大的威胁。因此，浅埋隧道的稳定性问题亟待于解决，而围岩压力的大小以及安全系数的取值成为目前研究的重点[1−3]。极限平衡法只考虑土体的平衡条件与屈服条件，却忽略了应力与应变的关系，而极限分析法恰恰弥补了这一缺点，以理想化的正交法则考虑了土体的本构关系，理论基础更为严密，逻辑思维更加清晰。因此，极限分析法被广泛应用于岩土工程中，从边坡的稳定性到土压力问题再到地基的承载力[4−6]。最近，极限分析法又被引入到隧道工程中，通过求解围岩压力、稳定性系数、破坏范围等来研究隧道的稳定性问题。Davis等[7]构建了浅埋隧道的破坏模式，基于线性破坏准则首次计算出稳定性系数和围岩压力的大小。Osman等[8]采用极限分析法推导出浅埋隧道围岩压力的表达式，并且通过改变参数值来研究围岩压力的变化规律。Klar等[9]利用极限分析法得到了围岩压力和稳定性系数的上限解，并且通过其变化规律来研究掌子面的稳定性。宋春霞等[10]针对非均质软黏土，运用极限分析法计算出围岩压力的上限解，并且探讨了掌子面稳定的影响因素。张箭等[11]基于已有掌子面的破坏模式，采用极限分析法研究浅埋隧道围岩压力与破坏面的演化特征，并且采用有限差分法验证了结果的正确性。另外，也有一部分学者从概率论的角度出发，考虑参数的随机特性，利用可靠度理论来分析浅埋隧道的稳定性问题。Low等[12]基于隧道顶部的楔形破坏模式，验证2种安全系数法的正确性，并且采用这2种方法来研究施作锚杆后隧道的可靠度。Mollon等[13−15]考虑参数的随机特性，采用可靠度理论来求解盾构隧道的失效概率以及安全支护力。苏永华等[16]为了解决计算结果的失真问题，将判别准则引入到可靠度程序中，提出了隧道可靠度响应面分析技术。张道兵等[17−18]针对衬砌结构，利用最大熵原理与可靠度理论来探讨浅埋隧道的稳定性问题。然而，上述研究并没有将极限分析法与可靠度有效地结合起来，而只是基于各自的原理单独地进行分析。更值得注意的是，上述文中所有土体材料都被假定服从线性破坏准则。而事实上，国内外大量试验证明土体服从非线性破坏准则，即线性只是其中一个特例[19−22]。因此，本文将非线性破坏准则引入到极限分析中，并且考虑参数的随机特性，即将极限分析非线性理论与可靠度理论有机地结合起来研究浅埋隧道的稳定性问题，为今后类似隧道的支护设计提供理论依据和参考价值。

1 极限分析非线性理论

国内外众多实验表明，土体发生破坏时剪应力与正应力表现为非线性关系，且非线性Mohr- Coulomb破坏准则的表达式为[19−20]：

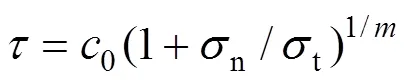
式中：τ和n为破坏面的剪应力和正应力；0为初始黏聚力；t为轴向拉应力；为非线性系数；并且0，t和可通过实验来确定。

当=1时，非线性破坏准则就退化成了线性破坏准则。在直角坐标系中，非线性破坏准则表现为一条曲线，若过曲线上的某点作一条切线，则切线的表达式为：

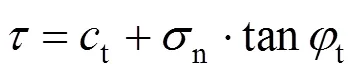
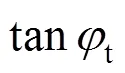
那么，联立式(1)和式(2)即可得非线性破坏准则下土体的抗剪强度指标，表达式为[21−22]：

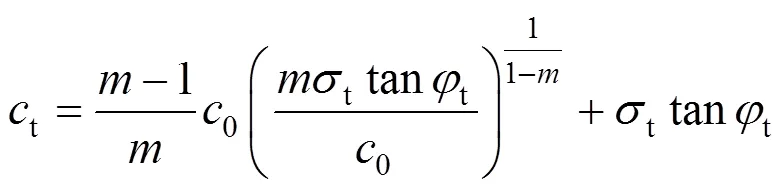
Chen[6]在阐述极限分析上限定理时认为，在机动许可的速度场中，外力所做功率与内部能量耗散功率相等所确定的荷载一定不小于实际的破坏荷载，并给出了相应的表达式，如下所示：

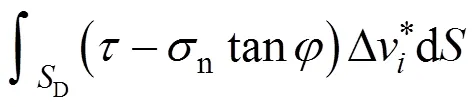
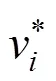
在进行计算时，将式(3)代入式(4)，即将非线性破坏准则引入到极限分析上限定理中，则所得到的解必定是真实值的一个上限解。

2 破坏模式与速度场

针对浅埋隧道，在已有的研究成果中，Davis等[7]构建了不排水黏土层的破坏模式，即=0的Tresca材料的破坏模式。但是，在实际工程中，土体一般属于库仑材料，即−土。因此，本文结合实际的工程情况，在Davis等研究成果的基础上加以改进，构建库仑材料下(−土)的破坏模式，并且根据极限分析上限定理的要求构建了运动许可的速度场，如图1所示。

在图1(a)中，隧道洞径为，埋深为，s为地表荷载，T为支护力，围岩压力为0。在破坏过程中，隧道上覆土体的速度为0，方向竖直向下，两侧间断线上的速度均为0.1，下方破坏面的速度均为1，且所有速度与其间断线之间的夹角均为t。在运动许可的速度场中，速度相容满足闭合条件，其矢量图如图1(b)所示。图1所示浅埋隧道破坏模式其适用条件为软弱围岩，即黏聚力和内摩擦角较小情况。

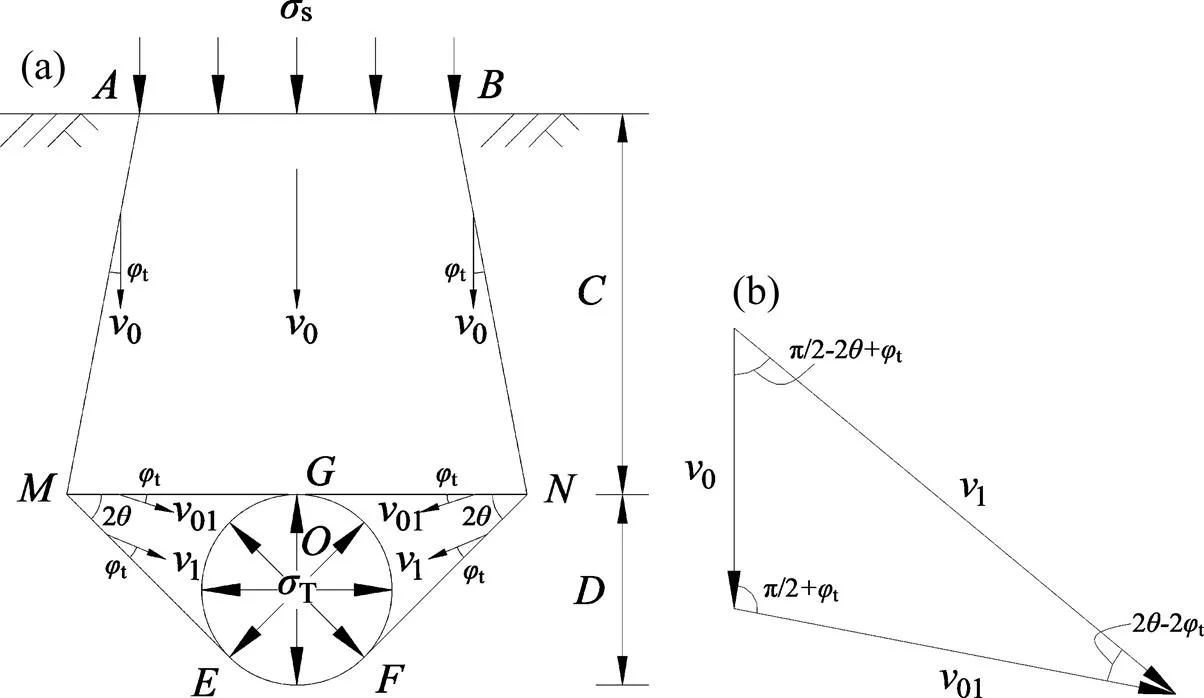
(a) 破坏模式；(b) 速度场

3 计算过程

根据极限分析上限定理的要求，本文做了如下假定：1) 破坏模式可视为二维平面应变问题处理；2) 对于隧道的稳定性问题，本构模型可采用理想弹塑性模型，土体且服从相关联的流动法则；3) 破坏模式中滑块为刚性块体，体积不发生变化，则能量仅沿速度间断线耗散。

对于隧道而言，围岩压力0相当于内力，为了求解围岩压力0，引入支护力T，在极限破坏状态下，所施加的支护力正好等于隧道破坏时的围岩压力，即0=T。此外，由于浅埋隧道的破坏模式具有对称性，只取一半结构进行计算。

3.1 速度关系

由于满足闭合条件，如图1(b)所示，速度之间的关系为：

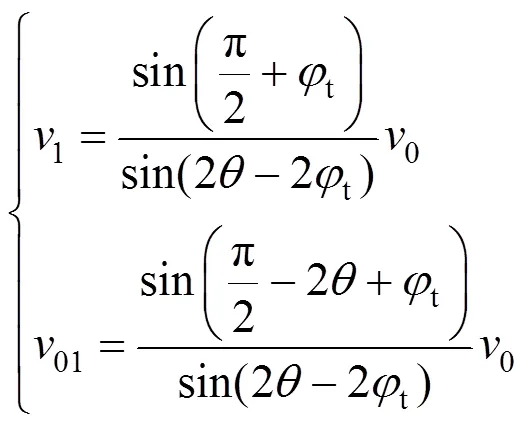
3.2 外力所做功率和内能耗散率

3.2.1 刚性块体间断线长度及其面积

由图1(a)可得，刚性滑块间断线长度及其面积的表达式如下：

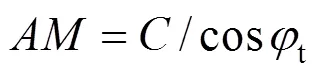
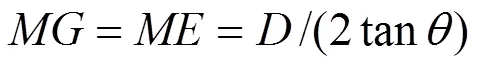
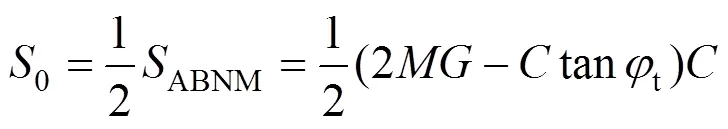
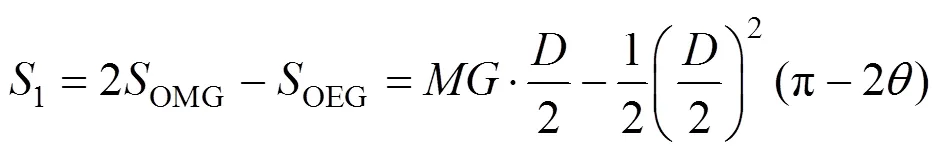
3.2.2 外力所做功率

1) 土体重力功率：

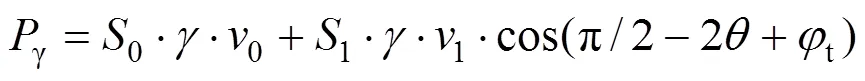
2) 地表荷载功率：

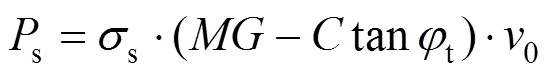
3) 支护力功率：

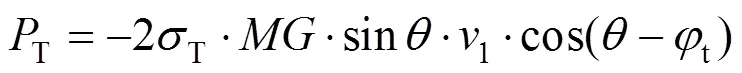
4) 内能耗散率：

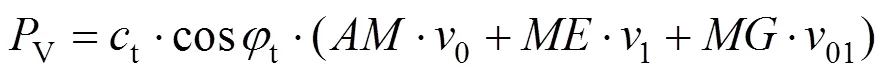
3.3 围岩压力

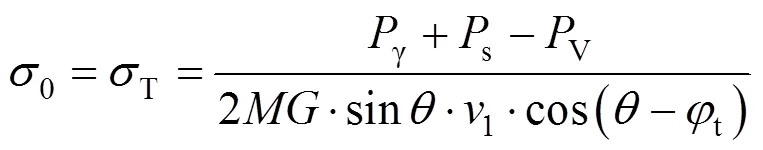
由图1(b)可得，浅埋隧道破坏模式的几何约束条件为：

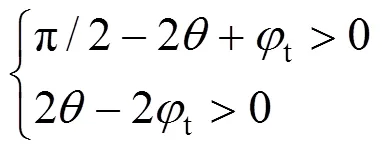
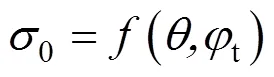
3.4 可靠度模型

若假定浅埋隧道支护设计的安全系数为s，则实际的支护力为：

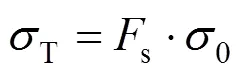
要使浅埋隧道不发生破坏，则必须满足：

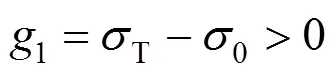
可靠度模型为：

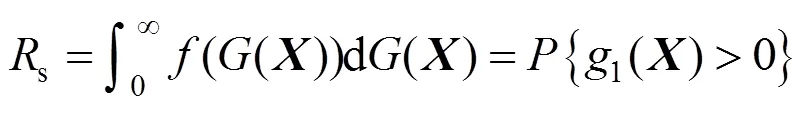
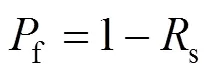
式中：s为可靠度；f为失效概率；与()分别为随机变量组成的向量与功能函数组成的向量，表达式分别为：

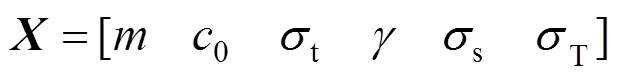
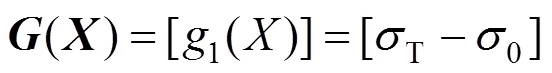
4 结果分析

4.1 对比验证

Davis等[7]采用稳定性系数来评价浅埋隧道的稳定状态。即：当≤6时，浅埋隧道处于稳定状态；当＞6时，浅埋隧道处于不稳定状态。具体表达式为：

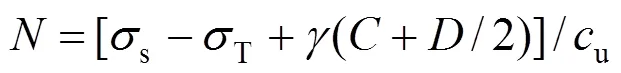
式中：s为地表荷载；T为支护力；为土体容重；为埋深；为洞径；u为土不排水时抗剪强度。

令非线性系数=1，即非线性破坏准则退化成线性破坏准则，在条件简化相同后，将本文稳定性系数与Davis等[7]研究成果进行了对比，如图2所示。其中参数为：s=0，t=0，/=1~4。另外，在图2中：(a)为无土重的情况，即/u=0；(b)为有土重的情况，且/u=2；(c)为有土重的情况，且/u=4。通过对比可得，在线性破坏准则下，本文稳定性系数的计算结果与Davis等[7]研究成果基本一致，最大误差在8%以内，验证了本文方法的正确性。

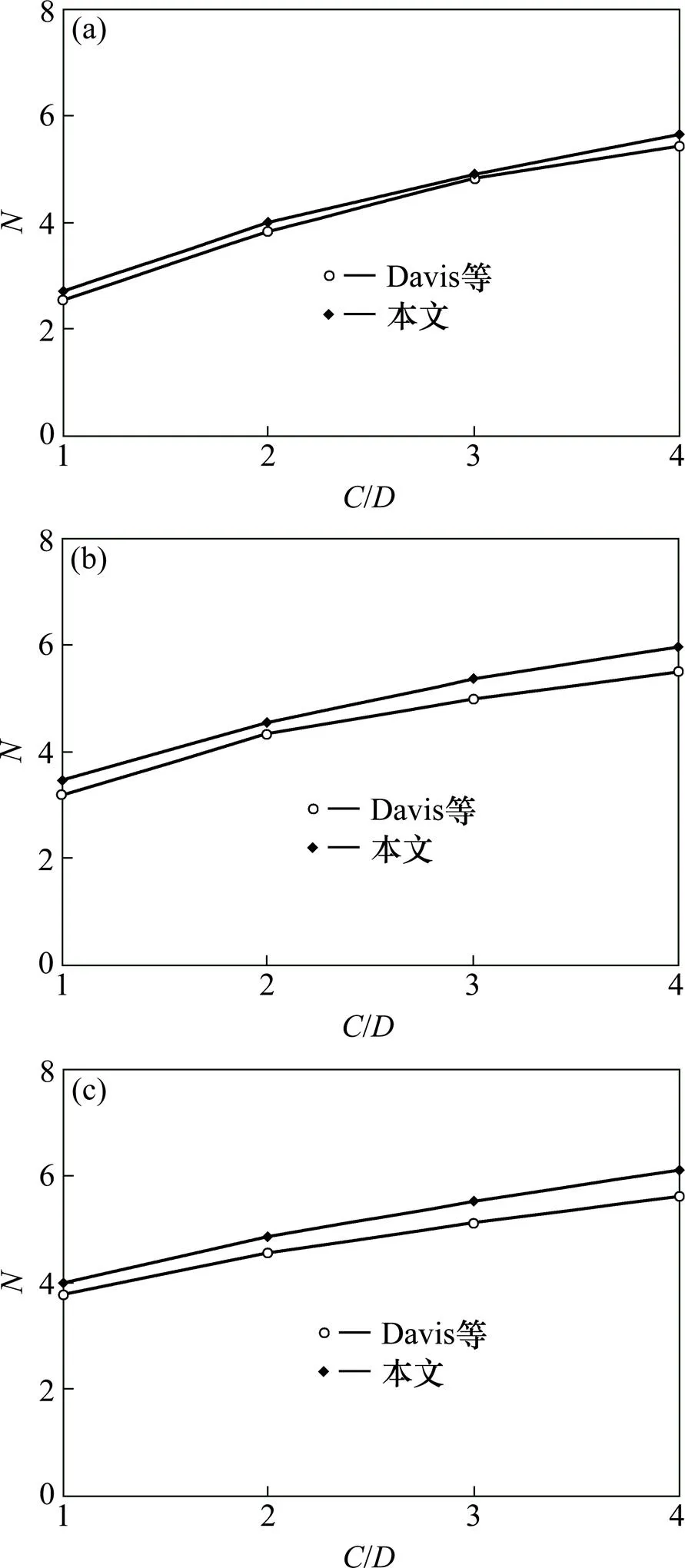
(a) γD/Cu=0；(b) γD/Cu=2；(c) γD/Cu=4

杨小礼等[23]采用极限分析上限定理得到了非线性破坏准则下浅埋隧道围岩压力的上限解。在参数相同的条件下，即：土体容重=20 kN/m3，埋深=20 m，洞径=10 m，初始黏聚力0=10 kPa，轴向拉应力t=30 kPa。基于本文方法所得到的围岩压力与杨小礼等[23]的计算结果进行了对比，如表1所示，当非线性系数=1.5~2.0时，本文计算结果与杨小礼等[23]基本一致，相对误差在5%以内，则进一步验证了本文方法的正确性。

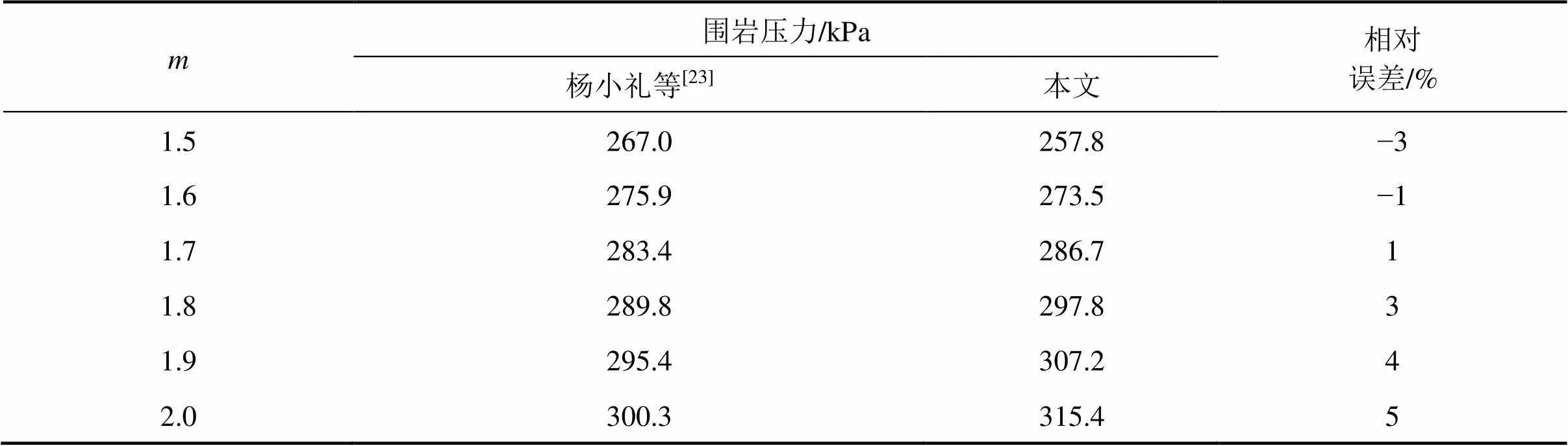
表1 非线性破坏准则下围岩压力对比

4.2 上限解分析

4.2.1 围岩压力

在非线性破坏准则下，各参数对浅埋隧道围岩压力的影响如图3所示。其中相应的参数为：埋深=20 m，洞径=10 m，土体容重=20 kN/m3，初始黏聚力0=10 kPa，轴向拉应力t=30 kPa，地表荷载s=100 kPa。由图3可知：1) 当非线性系数一定时，围岩压力0随埋深，地表荷载s以及土体容重的增加呈增大的趋势；而随初始黏聚力0的增加呈减小的趋势。2) 当所有参数一定时，围岩压力0随非线性系数的增加呈增大的趋势，且效果非常明显。由此可得，埋深、地表荷载、土体容重、初始黏聚力对围岩压力都有较大的影响，特别是非线性系数。所以，在对浅埋隧道进行支护设计时必须要考虑土体的非线性特性，防止因支护力过小或安全系数不足而引发坍塌事故。

4.2.2 破坏面

鉴于破坏面的演化规律比较相似，在这里只给出了非线性系数、地表荷载的破坏面，如图4所示。相应的参数为：埋深=20 m，洞径=10 m，土体容重=20 kN/m3，初始黏聚力0=10 kPa。从图4中可以看出，随着非线性系数、地表荷载的增大，浅埋隧道的破坏面呈向外扩展的趋势。这说明非线性系数与地表荷载对破坏面的位置有较大的影响，尤其是非线性系数，效果更加明显。所以，对于浅埋隧道围岩较差的地段，在开挖过程中产生的塑性区范围会较大，也较容易发生坍塌事故，建议及时进行监控量测以及加强支护措施。

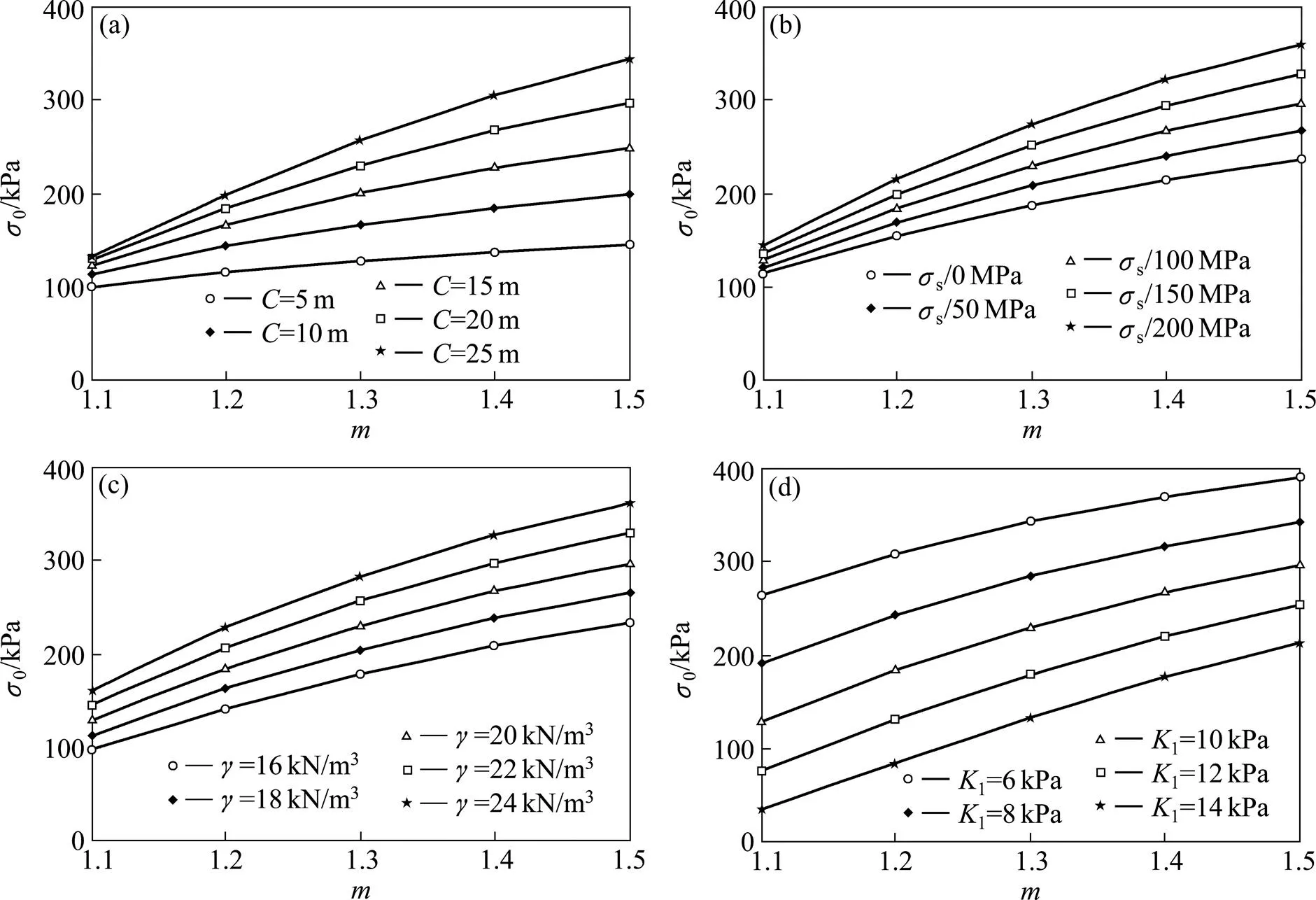
(a) m−C−σ0；(b) m−σs−σ0；(c) m−γ−σ0；(d) m−c0−σ0

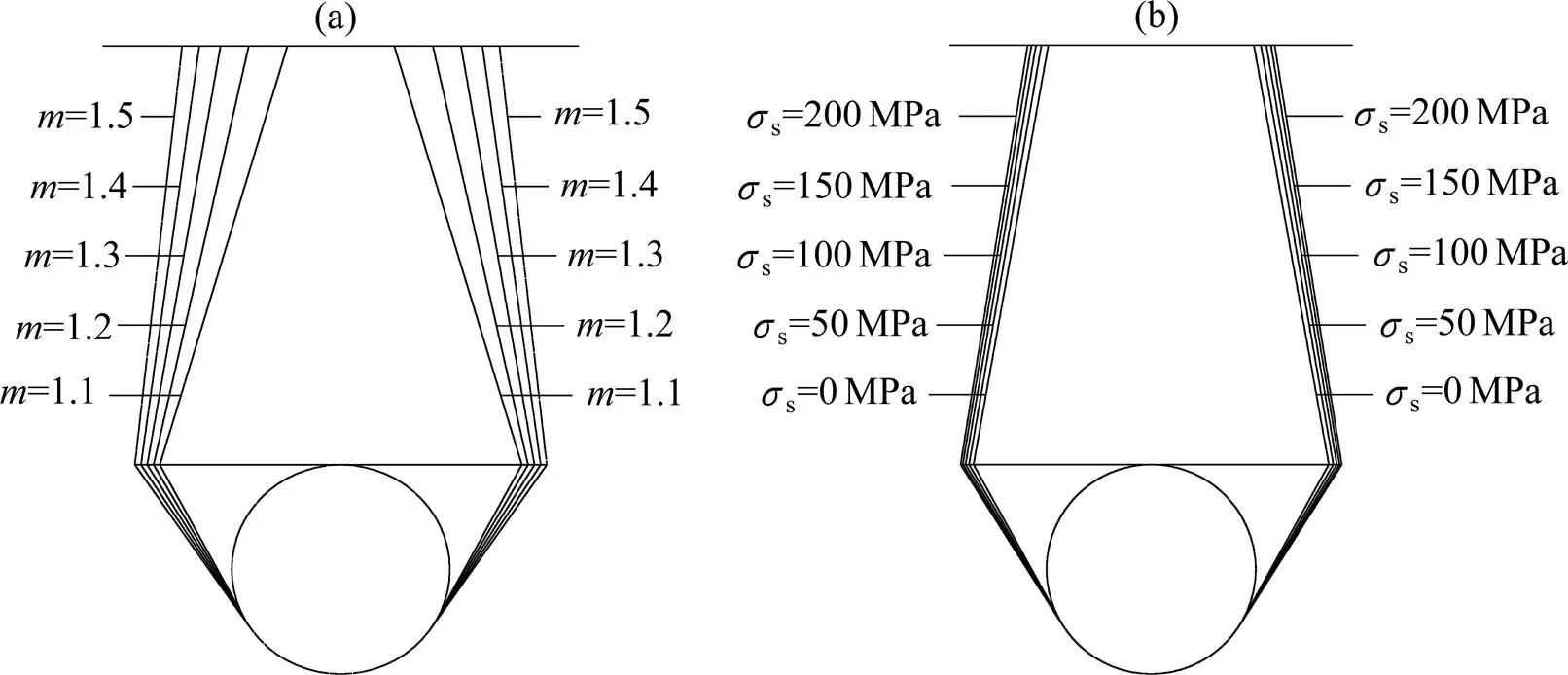
(a) 非线性系数对破坏面的影响(σs=10 kPa)；(b) 地表荷载对破坏面的影响(m=1.3)

4.3 可靠度分析

4.3.1 敏感性分析

参考已有研究成果[14, 24]，土体参数以及荷载服从正态分布或对数正态分布，且变异系数一般为0.1~0.35。为比较各参数的敏感性，假定土体参数和荷载服从同一种分布且变异系数相同，其统计特性如表2所示，其他相应参数为：埋深=20 m，洞径=10 m，安全系数s=1。浅埋隧道随机变量分布参数的敏感性如图5所示，通过对比可得，非线性系数对可靠度影响最敏感，初始黏聚力0与土体容重次之，而地表荷载s，支护力T以及轴向拉应力t都不太敏感，这说明非线性系数、初始黏聚力以及土体容重是影响浅埋隧道结构可靠度的主要因素。

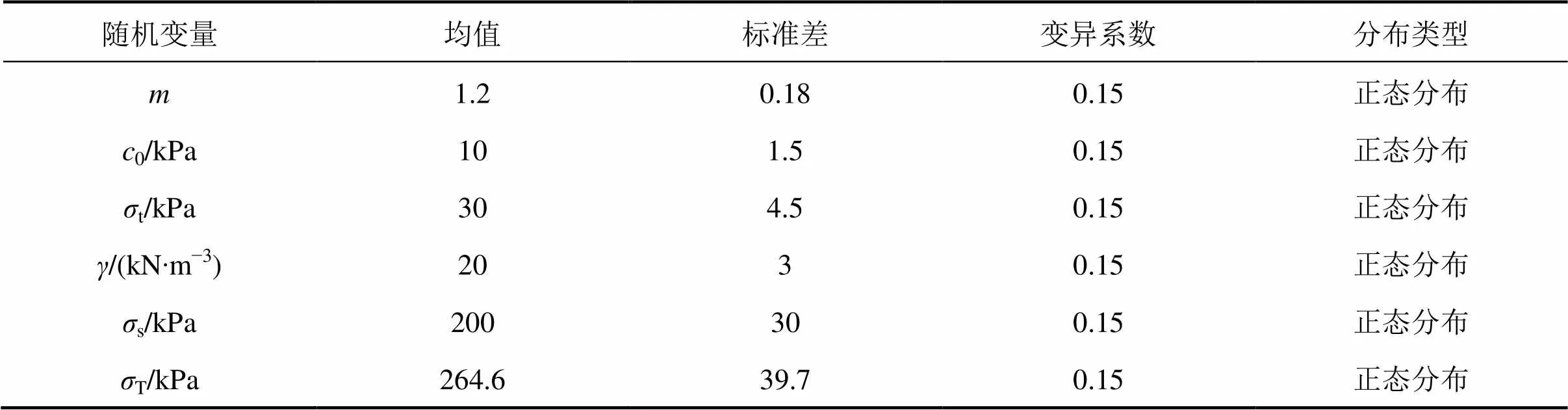
表2 随机变量的统计特性Ⅰ

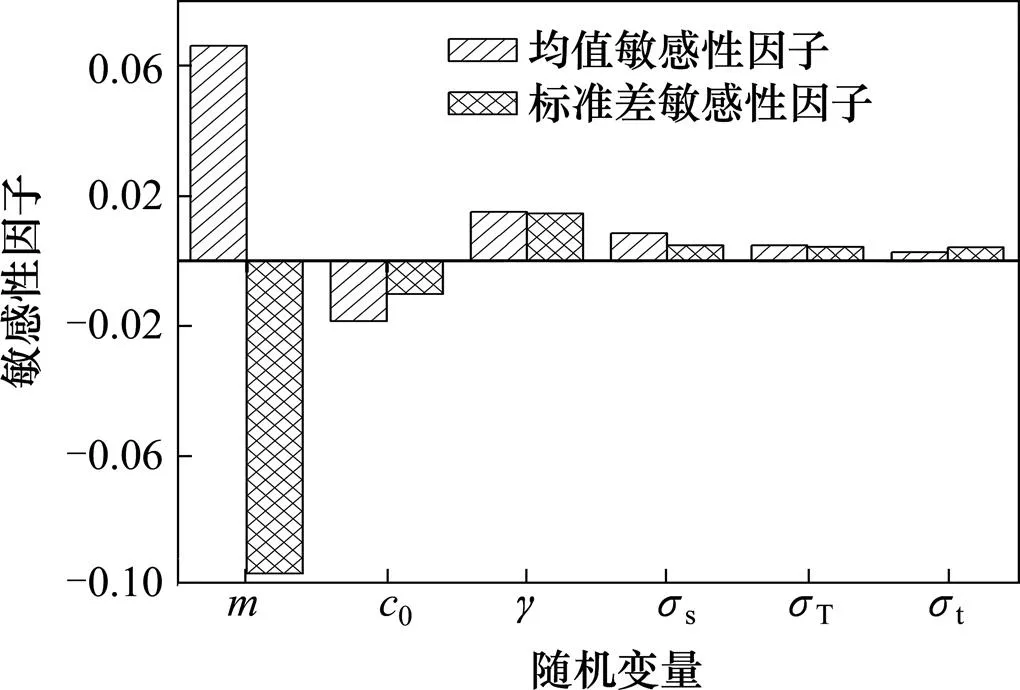
图5 随机变量分布参数敏感性因子对比

4.3.2 变异系数影响

为分析各参数变异系数的影响，假定变异系数的变化范围为0.01~0.30，其统计特性如表3所示，其他相应参数为：埋深=20 m，洞径=10 m，安全系数s=1.5。参数变异系数对浅埋隧道结构可靠度的影响如图6所示，随着参数变异系数的增大，可靠度均呈减小的趋势，尤其是非线性系数、土体容重以及支护力，效果比较明显。值得注意的是，整体变异系数发生变化时，可靠度增减幅度更大，可见单一参数变异系数影响为整体变异系数影响起到了叠加的效应。

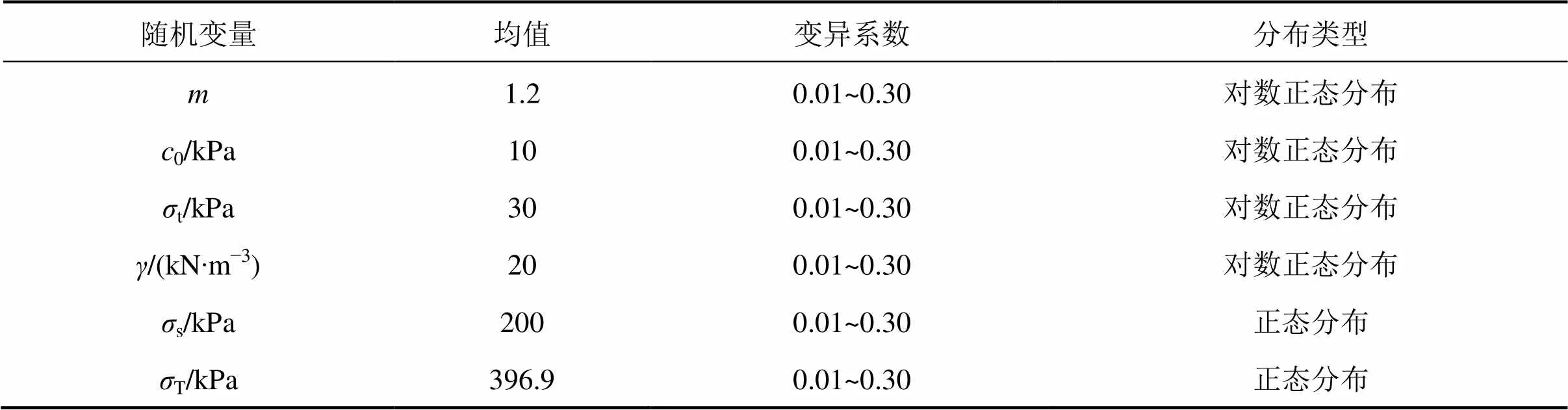
表3 随机变量的统计特性Ⅱ

图6 各参数变异系数对可靠度的影响

4.3.3 安全系数与支护力

为分析非线性破坏准则对浅埋隧道稳定性的影响，令非线性系数均值为1.1~1.5，各参数统计特性如表4所示，其他相应参数为：埋深=20 m，洞径=10 m。根据《铁路隧道设计规范》引入表5中的目标可靠指标[][25]，在不同安全等级下，浅埋隧道所需要的最小安全系数与最小支护力，如表6~7所示。以表7为例进行分析，当非线性系数从1.1增大到1.5时，围岩压力从200.0 kPa增大到389.2 kPa，增长率达到95%，满足安全等级3所需要的支护力从490.0 kPa增大到899.1 kPa，增长率达到83%；满足安全等级2所需要的支护力从588.0 kPa增大到1 004.1 kPa，增长率达到71%；满足安全等级1所需要的支护力从706.0 kPa增大到 1 249.3 kPa，增长率达到77%。此外，支护力还随安全等级的升高而增大，以=1.1为例，满足安全等级3，2和1所需要的支护力分别为490.0，588.0和706.0 kPa，增长率均为20%。由此可见，与安全等级相比较，非线性系数对支护力的影响更大。综上所述，非线性系数对浅埋隧道破坏时的围岩压力以及满足安全等级所需要的支护力有着显著的影响，如果不考虑破坏准则的非线性，则低估了隧道破坏时的围岩压力，从而支护力也达不到安全等级的要求。安全系数并没有随非线性系数的增大发生明显的变化，只是略呈减小的趋势，安全系数的变化更取决于安全等级。以=1.1为例，满足安全等级3，2和1所需要的安全系数分别为2.45，2.94和3.53，增长率均为20%。

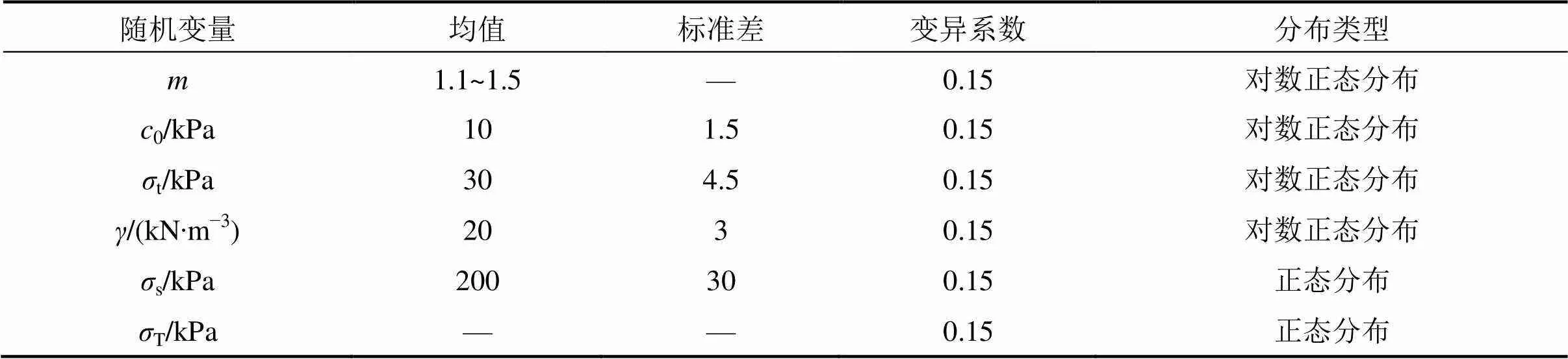
表4 随机变量的统计特性Ⅲ

表5 隧道结构目标可靠指标[β]值

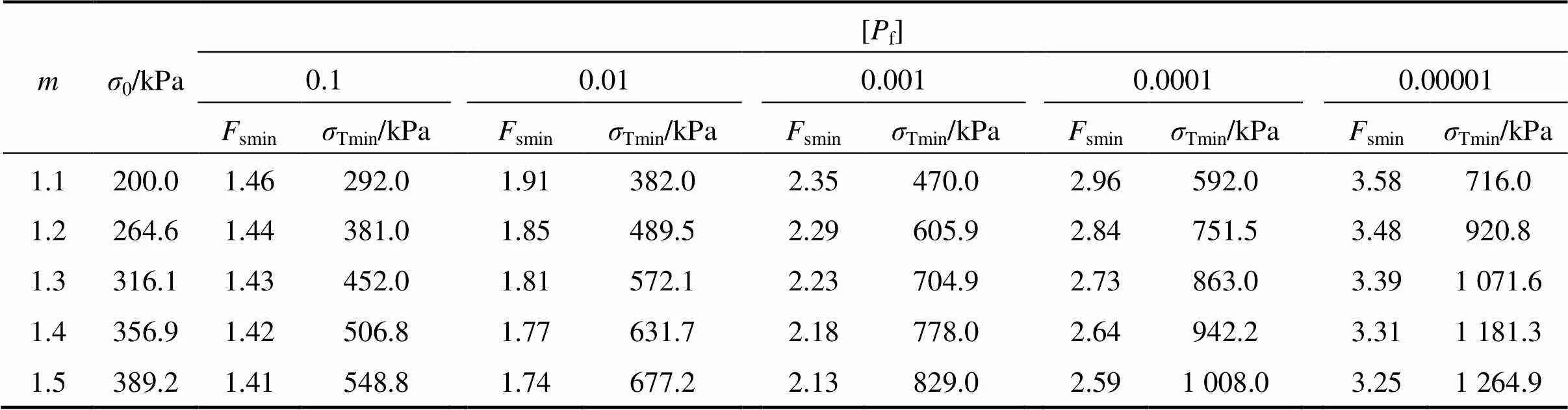
表6 容许失效概率下的最小安全系数与最小支护力

表7 目标可靠指标下的最小安全系数与最小支护力

5 结论

1) 在非线性破坏准则下，采用极限分析上限定理得到了浅埋隧道破坏时的围岩压力以及破坏范围。将本文计算结果与文献[7]研究成果进行对比，吻合良好，验证了本文方法的正确性。

2) 非线性系数对浅埋隧道破坏时的围岩压力以及破坏范围都有很大的影响。即随着非线性系数的增加，围岩压力增大，增长率可达到95%，破坏面向外扩展，破坏范围也呈增大的趋势。

3) 很显然，安全等级决定着支护力和安全系数的大小。对于支护力而言，非线性系数的影响更为显著，增长率可达到83%，安全等级的影响却只有20%。但是，安全系数的大小更取决于安全等级，增长率均为20%。

[1] 杨峰, 阳军生. 浅埋隧道围岩压力确定的极限分析方法[J]. 工程力学, 2008, 25(7): 179−184. YANG Feng, YANG Junsheng. Limit analysis method for determination of earth pressure on shallow tunnel[J]. Engineering Mechanics, 2008, 25(7): 179−184.

[2] 许敬叔, 潘秋景. 盾构隧道开挖面支护力上限分析[J]. 铁道科学与工程学报, 2014, 11(4): 80−84. XU Jingshu, PAN Qiujing. Upper bound analysis of supporting pressure for shield tunnel faces[J]. Journal of Railway Science and Engineering, 2014, 11(4): 80−84.

[3] 周宗青, 李术才, 李利平, 等. 浅埋隧道塌方地质灾害成因及风险控制[J]. 岩土力学, 2013, 34(5): 1375−1382. ZHOU Zongqing, LI Shucai, LI Liping, et al. Causes of geological hazards and risk control of collapse in shallow tunnels[J]. Rock and Soil Mechanics, 2013, 34(5): 1375− 1382.

[4] 李大钟, 郑榕明, 王金安, 等. 自适应有限元极限分析及岩土工程中的应用[J]. 岩土工程学报, 2013, 35(5): 922−929. LI Dazhong, ZHENG Rongming, WANG Jinan, et al. Application of finite-element-based limit analysis with mesh adaptation in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(5): 922− 929.

[5] 赵炼恒, 罗强, 李亮, 等. 层状岩体边坡动态稳定性拟静力上限分析[J]. 岩土力学, 2010, 31(11): 3627−3634. ZHAO Lianheng, LUO Qiang, LI Liang, et al. Upper bound quasi-static analysis of dynamic stability of layered rock slopes[J]. Rock and Soil Mechanics, 2010, 31(11): 3627−3634.

[6] Chen W F. Limit analysis and soil plasticity[M]. Florida: J Ross Publishing, Inc, 2007.

[7] Davis E H, Gunn M J, Mair R J, et al. The stability of shallow tunnels and underground openings in cohesive material[J]. Geotechnique, 1980, 30(4): 397−416.

[8] Osman A S, Mair R J, Bolton M D. On the kinematics of 2D tunnel collapse in undrained clay[J]. Geotechnique, 2006, 56(9): 585−595.

[9] Klar A, Osman A S, Bolton M. 2D and 3D upper bound solutions for tunnel excavation using elastic flow fields[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(12): 1367−1374.

[10] 宋春霞, 黄茂松, 吕玺琳. 非均质地基中平面应变隧道开挖面稳定上限分析[J]. 岩土力学, 2011, 32(9): 2645− 2650. SONG Chunxia, HUANG Maosong, LÜ Xilin. Upper bound analysis of plane strain tunnel in nonhomogeneous clays[J]. Rock and Soil Mechanics, 2011, 32(9): 2645− 2650.

[11] 张箭, 杨峰, 刘志, 等. 浅覆盾构隧道开挖面挤出刚性锥体破坏模式极限分析[J]. 岩土工程学报, 2014, 36(7): 1344−1349. ZHANG Jian, YANG Feng, LIU Zhi, et al. Three-dimensional limit analysis of blow-out failure modes of shallow shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1344−1349.

[12] Low B K, Einstein H H. Reliability analysis of roof wedges and rockbolt forces in tunnels[J]. Tunnelling and Underground Space Technology, 2013, 38: 1−10.

[13] Mollon G, Dias D, Soubra A H. Rotational failure mechanisms for the face stability analysi of tunnels driven by a pressurized shield[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363−1388.

[14] Mollon G, Dias D, Soubra A H. Range of the safe retaining pressures of a pressurized tunnel face by a probabilistic approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(11): 1954− 1967.

[15] Mollon G, Dias D, Soubra A H. Probabilistic analyses of tunneling-induced ground movements[J]. Acta Geotechnica, 2013, 8(2): 181−199.

[16] 苏永华, 李翔, 丁云, 等. 基于二次正交试验优化的隧道围岩稳定可靠度方法[J]. 岩土工程学报, 2012, 34(2): 326−332. SU Yonghua, LI Xiang, DING Yun, et al. Reliability degree method for stability of surrounding rock of tunnels based on quadratic orthogonal experimental optimization [J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 326−332.

[17] 张道兵, 杨小礼, 朱川曲. 基于可靠度理论与Matlab的隧道衬砌结构设计与分析[J]. 采矿与安全工程学报, 2011, 28(2): 323−327. ZHANG Daobing, YANG Xiaoli, ZHU Chuanqu. Design and analysis of tunnel lining structure based on reliability theory and Matlab[J]. Journal of Mining & Safety Engineering, 2011, 28(2): 323−327.

[18] 张道兵, 杨小礼, 朱川曲, 等. 基于最大熵原理与最优化方法的隧道衬砌结构可靠度分析[J]. 中南大学学报 (自然科学版), 2012, 43(2): 663−668. ZHANG Daobing, YANG Xiaoli, ZHU Chuanqu, et al. Structural reliability analysis of tunnel lining based on maximal entropy principle and optimization method[J]. Journal of Central South University (Science and Technology), 2012, 43(2): 663−668.

[19] YANG Xiaoli. Seismic passive pressures of earth structures by nonlinear optimization[J]. Archive of Applied Mechanics, 2011, 81(9): 1195−1202.

[20] YANG Xiaoli, ZHANG Daobing, WANG Zuowei. Upper bound solutions for supporting pressures of shallow tunnels with nonlinear failure criterion[J]. Journal of Central South University, 2013, 20(7): 2034−2040.

[21] YANG Xiaoli, YANG Zihan, LI Yongxin, et al. Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique[J]. Journal of Central South University, 2013, 20(12): 3676−3682.

[22] YANG Xiaoli, YANG Zihan, PAN Qiujing, et al. Kinematical analysis of highway tunnel collapse using nonlinear failure criterion[J]. Journal of Central South University, 2014, 21(1): 381−386.

[23] 杨小礼, 王作伟. 非线性破坏准则下浅埋隧道围岩压力的极限分析[J]. 中南大学学报(自然科学版), 2010, 41(01): 299−302. YANG Xiaoli, WANG Zuowei. Limit analysis of earth pressure on shallow tunnel using nonlinear failure criterion[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 299−302.

[24] 谢桂华. 岩土参数随机性分析与边坡稳定可靠度研究[D]. 长沙: 中南大学, 2009. XIE Guihua. Stochastic analysis of geotechnical parameters and study on stable reliability of slope[D]. Changsha: Central South University, 2009.

[25] TB 10003—2005, 铁路隧道设计规范[S]. TB 10003—2005, Specification for railway tunnel design[S].

(编辑 阳丽霞)

Upper bound solutions of support parameter for shallow tunnels in nonlinear soil masses

ZHANG Jiahua1, 2, ZHANG Biao3

(1. Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China; 2. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China; 3. School of Civil Engineering, Central South University, Changsha 410075, China)

Due to the nonlinear characteristic of failure criterion and variation of parameters, the stability of shallow tunnels was analyzed in this work with limit analysis nonlinear theory and reliability approach. The results show that the calculation solutions are in accordance with the existing results when the nonlinear failure criterion degrades to the linear one, which verifies the validity and correctness of proposed method in this paper. In the analysis of upper bound solutions, the nonlinear coefficient has significant impact on collapse pressure and failure range, thus the nonlinear property of soils should be taken into account in the process of bracing design so as to prevent collapse issues owing to insufficient supporting pressure and safety factor. Further, in the calculation process of reliability, the nonlinear coefficient is the dominating factor affecting reliability. Safety factor and supporting pressure were derived under 3 safety levels for shallow tunnels, which can be regarded as supplement of design criterion in tunnel engineering, and provide reference value for the design of shallow tunnels.

shallow tunnel; nonlinear failure criterion; limit analysis; reliability; safety factor; supporting pressure

10.19713/j.cnki.43−1423/u.2018.08.021

TU43

A

1672 − 7029(2018)08 − 2062 − 10

2017−06−06

国家自然科学基金资助项目(51434006，51374105)；湖南科技大学博士启动基金资助项目(E51768)；湖南科技大学博士后科研基金资助项目(E61610)；南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室开放基金资助项目(E21734)

张佳华(1983−)，男，湖北天门人，讲师，博士，从事隧道与地下工程方面研究；E−mail：1010090@hnust.edu.cn