接触网复合绝缘子污闪电压预测方法研究

王思华，曹丽明，景弘



接触网复合绝缘子污闪电压预测方法研究

王思华1，曹丽明1，景弘2

(1. 兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2. 国网平凉供电公司，甘肃 平凉 744000)

通过人工污秽实验室中对接触网常用的11种复合绝缘子进行大量污秽实验，提出一种基于改进生物地理学算法优化BP神经网络的接触网复合绝缘子临界污闪电压预测模型。选取伞径m，爬电距离，形状因数及等值附盐密度ESDD作为模型的输入特征量。试验和对比分析表明，模型的预测效果良好，预测结果与试验结果基本一致。预测值可作为污闪试验的参考数据，能够有效降低污闪试验的工作量，为评估接触网线路的可靠性及对新建线路外绝缘的选型和维护提供一条新思路。

复合绝缘子；污闪；污秽试验；临界污闪电压预测；生物地理学算法；BP神经网络

从20世纪90年代末开始，硅橡胶复合绝缘子逐渐在电气化铁路接触网上大规模推广使用。与传统的瓷质绝缘子相比，其具有良好的憎水性和抗污闪能力强等优点。在电气化铁路接触网设备防污闪方面起着重要作用。目前，我国复合绝缘子运行基本处于“免维护”状态，不同时期、不同厂家和不同工艺生产的复合绝缘子在恶劣的运行环境下是否都能“免维护”是值得一个令人深思的问题。运行经验表明：复合绝缘子在外界恶劣运行环境、电气因素、机械因素等共同作用下机电性能会逐渐下降。复合绝缘子抗污闪能力强并不代表其不会发生污秽闪络现象，运行中的复合绝缘子也会发生污闪事故[1−2]。由于复合绝缘子有着其独特的污闪特性，同时在我国电气化铁路从试运行到大面积推广使用只走过不到20 a时间，人们对其一些特性远没有达到完全掌握的程度。所以探索复合绝缘子的污闪电压预测方法具有非常重要的意义。目前，国内外在绝缘子污闪电压预测方面做了很多研究，大体来说预测污闪电压应用较多的数学方法是神经网络、支持向量机回归和最小二乘回归。Kontargyri等[3−4]利用BP神经网络模型预测绝缘子的临界闪络电压。虽然BP神经网络有较强的学习能力但该方法并不能保证得到全局最优解。舒立春等[5−6]利用支持向量机回归来预测恶劣气候条件下绝缘子的污闪电压。其存在着数据计算量大，运算速度较慢的缺点。Shewhdi等[7−8]利用传统最小二乘回归分析来预测不同绝缘介质的闪络电压和绝缘强度。由于该方法对误差做了正态假设，故不具有稳健性。这些文献多从定性的角度提出绝缘子污闪电压预测的方法，对影响绝缘子污闪电压的因素和污闪发生规律进行了深入研究。但由于受电气化铁路接触网运行环境的多样性、污闪机理的复杂性、污闪实验经济性的限制。以上研究成果还存在一定的不足，当前污闪事故仍未得到彻底根治。因此很有必要对接触网绝缘子的污闪电压预测方法进行深入研究。本文首先选定接触网常用的11种复合绝缘子作为研究对象，建立基于改进生物地理学算法优化BP神经网络的接触网复合绝缘子临界污闪电压预测模型。以大量人工污秽试验的试验数据作为训练和测试样本，利用训练好的BP神经网络来预测复合绝缘子的临界污闪电压，并将结果与生物地理学算法优化BP神经网络、BP神经网络预测的临界污闪电压进行对比，验证本文所提方法的可行性和有效性。对提高电气化铁路接触网供电系统的可靠性以及降低污闪试验的工作量提供了一条新的思路。

1 复合绝缘子临界污闪电压预测模型的建立

1.1 生物地理学算法

生物地理学是一门研究生物群落及其组成部分在时间和空间上分布的独立学科，起源于19世纪。国内外学者对其进行了深入研究，提出了众多关于生物群落的分布、迁移和灭绝的数学模型。Boussaid等[9−10]受这些数学模型的启发于2008年提出了生物地理学优化算法(biogeography-based optimization，BBO)。BBO算法通过建立物种数量与迁入率和迁出率的迁移模型，依靠相邻个体的迁移和个别个体的突变。求出各个栖息地的适应度，达到寻求目标函数全局最优解的目的。

在生物地理学中，个体对应生物地理学数学模型中的栖息地；个体的变量对应模型中适应度指数变量(SIV)；个体的适应度对应模型中栖息地适应度指数(HSI)；优秀个体对应模型中HSI较高的栖息地；在BBO算法中优化函数适应值通过适应度指数表示，HSI较高的栖息地对应着一个较好的候选解，HSI较低的栖息地对应着一个较差的候选解。物种在栖息地之间的迁移使得一些低HSI解集能从高HSI的解集获取有益的新特征，其解集的适应度得以提高。BBO算法包括初始化、迁移操作和变异操作等3个步骤。

1.2 生物地理学算法的改进

BBO算法尽管具有很多优点，但其一些缺陷限制了它的应用范围。比如迁移机制比较离散，迁移时无方向性。这致使算法的收敛精度和收敛速度不理想。本文将混沌理论引入到生物地理学算法中，提出一种基于混沌理论的生物地理学优化算法(CS-BBO)。把BBO算法对全局最优解寻优较快的能力和CS算法寻优精度和效率较高的优点相结合，从而提升了BBO算法的收敛速度和收敛精度。BBO算法的具体改进措施如下：

1) 初始化方法的变化：基本BBO算法的种群初始化方法为整数编码，在CS-BBO算法中构建混沌初始化，利用实数编码和分段logistic混沌映射生成初始栖息地SIV。

2) 迁移策略的调整：基本BBO算法采用的是离散迁移机制，迁移操作具有一定的盲目性和局限性。本文对迁移机制引入方向性的扰动，采用混合迁移策略使迁移替代具有“趋向性”，增强了局部搜索能力。

3) 变异策略的调整：引入退化混沌变异算子来模拟进化过程，即在变异的过程中根据进化的不同阶段设置不同的变异率，通过变异算子控制变异行为，避免了基本BBO算法易产生差解的缺陷。

4) 最终解确定方法的变化：首先利用基本BBO算法得到一组解集，在这组解的基础上进行混沌迭代搜素，生成一组新的解集。计算并比较这两组解集的HSI，HSI最优对应的那个解集即为最终解集。

1.3 CS-BBO算法优化BP神经网络

本文将CS-BBO算法与BP神经网络有机的结合起来，利用CS-BBO算法作为学习算法来优化BP神经网络的权值和阈值，来弥补BP神经网络算法易陷入局部最优的缺陷。即将BP神经网络的权值和阈值映射为生物栖息地的物种，通过对迁移过程中迁移策略，迁入率和迁出率的调整来计算栖息地的适应度。得到的最优化初值作为BP神经网络的初始权值和阈值，经过CS-BBO算法优化BP神经网络，能使其误差函数最小化。此时适应度函数如式(1)所示。

利用CS-BBO算法优化BP神经网络的流程为：

1) 混沌初始化BP神经网络的参数，确定网络结构。设定网络输入层、输出层和隐含层神经元个数。

2) 初始化CS-BBO算法的最大种群数量max，最大迁移率max，max，最大变异率max，栖息地个数等参数。

3) 在栖息地适应度向量与BP神经网络权值、阈值之间完成映射，按照式(1)求出每个个体的适应度值并映射给每个物种。当适应度函数达到最小或达到最大迭代次数(停止条件)时，输出最优解，否则进行步骤4。

4) 计算每个栖息地的迁入、迁出率，运用混合迁移策略执行迁移操作。对群体执行基于退化混沌变异算子的变异操作来更新物种，对得到的新物种群体进行最终的混沌搜索，重新计算各个栖息地的适应度值，保留最优解。

5) 判断是否满足停止条件，若满足条件则停止，输出最优解。否则返回到第3步进行下一次 迭代。

6) 将CS-BBO算法优化BP神经网络后得到的优化初值作为BP神经网络的初始权值和阈值，对网络进行训练，检验网络泛化能力，得到最佳网络模型。具体流程图如图1所示。

1.4 预测模型输入特征量的选择

1958年德国学者Obenaus提出了污秽放电物理模型，其广泛应用与瓷和玻璃绝缘子污闪特性分析。希腊学者Topalis在Obenaus模型的基础上提出悬式绝缘子的临界污闪电压C的计算公式为：

其中：

式中：n和N为沿面电弧静态常数。本文中取n=0.67，N=140；L为爬电距离，cm；Dm为绝缘子的最大伞径，cm；f为绝缘子的形状系数；K为剩余污层电阻系数；δs为污秽绝缘子表面电导，S；r为弧足半径，cm。

黄成才等[11−12]通过大量试验研究，提出对于复合绝缘子的污闪分析仍然可以采用Obenaus模型，仅需将模型中剩余污层替换为剩余水带即可。根据以上模型可知，绝缘子的临界污闪电压C受多种因素的影响，理论上考虑的影响因素越多越好，但根据可行性、实用性和直观性原则。本文选取复合绝缘子的最大伞径m，爬电距离，形状因素和等值附盐密度ESDD等4个指标作为预测模型的输入特征量，绝缘子的临界污闪电压作为预测模型的输出特征量。以东莞高能电气公司生产的接触网常用的11种铁道复合绝缘子作为试品进行人工污秽试验，试验数据作为预测模型的训练和检测样本。试品参数如表1所示。为了提高BP神经网络的计算精度和泛化能力，对数据做归一化处理，处理方法如式(7)所示。

式中：max和min分别为指标的最大，最小值。*为指标归一化后的值，数值大小在[0,1]范围内。

表1 试品参数

2 试验方案

2.1 试验装置

试验在人工雾室中进行，通过调压器和变压器将工频380 V电压转换为所需电压。把人工雾室中垂直悬挂的接触网复合绝缘子球头侧接到穿墙套管上，球帽侧接地。变压器的额定容量和额定电流分别为50 kV∙A和1 A，短路阻抗为8.23%。系统的阻抗电压小于9.5%。满足IEC对交流污秽试验电源的要求。试验原理如图2所示。

2.2 试品染污

根据GB/T4585—2004、DL/T859—2004等试验标准，采用固体涂层法对复合绝缘子进行人工污秽试验[13−14]。导电物质采用商业用纯Nacl进行模拟，不溶性物质采用硅藻土进行模拟。选取盐密ESDD为0.05，0.10，0.15和0.20 mg/cm2；灰密NSDD为2.0 mg/cm2。由试品表面积及所选取的盐密、灰密值计算出每只绝缘子所需的NaCl和硅藻土的量。使用电子天平(可精确到0.1 mg)称量出所需物质(NaCl误差≤±1%，硅藻土误差≤10%)。将适量去离子水(电导率＜0.001 S/m)倒入到NaCl和硅藻土的混合物中并搅拌调匀，用小刷子将污液均匀涂刷在复合绝缘子表面，此过程在1 h内完成。悬挂静止24 h让其完全阴干待试。

图2 试验原理图

2.3 人工污秽试验

试验正式开始前，首先对试品进行编号。按照表1中复合绝缘子的次序将型号依次变为1~11号。把染污的复合绝缘子垂直悬挂于人工雾室顶部，复合绝缘子与环境温差＜±2 K，采用全自动蒸汽发生器来生成蒸汽雾使试品湿润，设置蒸汽雾输入速率为0.05±0.01 kg/h，人工雾室温度控制在＜35 ℃。试验开始后，对试品施加试验电压，同时通入蒸汽。运用恒压升降法获取试品的50%污闪电压[15]。数值计算公式如式(8)所示，试验结果如表2所示。

式中：U为试品所施加的试验电压；n为U下进行的试验次数；为有效实验次数。

表2 人工污秽试验结果

3 CS-BBO算法优化BP神经网络在复合绝缘子临界污闪电压预测中的应用

3.1 临界污闪电压的预测

本文选取3层型BP神经网络，设定输入层神经元个数为，输出层神经元个数为，隐含层神经元个数为1，期望输出与实际输出之间的误差平方和作为误差函数。其中隐含层神经元个数1和误差函数由式(9)~(10)来确定。

隐含层神经元传递函数采用函数，输出层采用purelin函数。输入层神经元个数为4个，输出层神经元个数为1个，隐含层神经元个数由式(9)初步确定为6个。使用循环函数进行Matlab编程，当选取隐含层神经元个数为4~8，误差函数为0.001时发现都能顺利收敛，所用步数如表3所示。其中MSE为均方误差，EPOCHS为训练步数。从表3可以看出，当隐含层神经元个数为6时，此时收敛的最快。所以确定隐含层神经元个数为6。

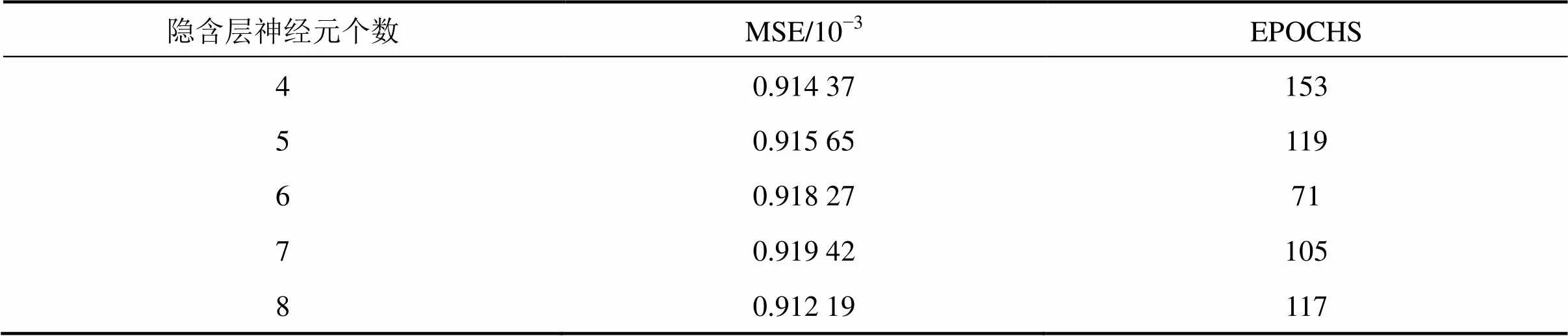
表3 不同隐含层神经元的网络误差和训练次数

使用CS-BBO算法来训练BP神经网络，设定最大种群数max=100，迁移率==1.0，最大突变率max=0.5，栖息地个数=100，最大迭代次数max=200，网络的误差精度为0.001。将人工污秽试验得到的44组试验数据分为2部分，前32组试验数据作为训练样本，后12组试验数据作为检测 样本。

图3为CS-BBO算法和BBO算法分别对BP神经网络训练的对比曲线。从图4可以看出：CS-BBO算法优化BP神经网络只需69次训练即可达到目标，而BBO算法需要训练123次。前者收敛速度快，全局搜索能力强，能更快的找到全局最优点。经计算，利用CS-BBO算法训练BP神经网络的均方差为0.312 7，而BBO算法训练BP神经网络的均方差为0.658 3。可见CS-BBO算法不仅提高了BP神经网络的处理速度，同时提高了BP神经网络的训练精度。综上可以看出，CS-BBO算法优化后的BP神经网络能够很好的克服其易陷入局部最优解的缺陷。在相同的训练次数下，得到的结果更精确。

图3 CS-BBO算法和BBO算法分别优化BP神经网络的训练结果

3.2 对比和分析

利用训练好的BP神经网络预测接触网复合绝缘子的临界污闪电压。检测样本数据和复合绝缘子临界污闪电压预测结果如表4所示。计算12组检测样本数据的预测结果与人工污秽试验结果之间的误差进行对比分析，误差分析结果如表5所示。其中为复合绝缘子临界污闪电压的相对误差；Δ为复合绝缘子临界污闪电压的绝对误差。

从表4可以看出，同一型号复合绝缘子其临界污闪电压随着ESDD的增加而降低，说明污秽程度对复合绝缘子的临界污闪电压影响较大。不同型号的复合绝缘子在相同的ESDD下，临界污闪电压值也有着较大的差异。说明伞径m，爬电距离和形状因素等参数均对复合绝缘子的临界污闪电压有影响。从表5中可以看出，表5的平均相对误差为3.91%，试验结果与预测结果最大误差不超过9%，故满足了工程需要。因此利用CS-BBO算法优化BP神经网络建立的接触网复合绝缘子临界污闪电压预测模型的方法是可行的，临界污闪电压的预测值与试验值基本符合，预测效果良好。证明了本文所提方法的正确性和有效性。

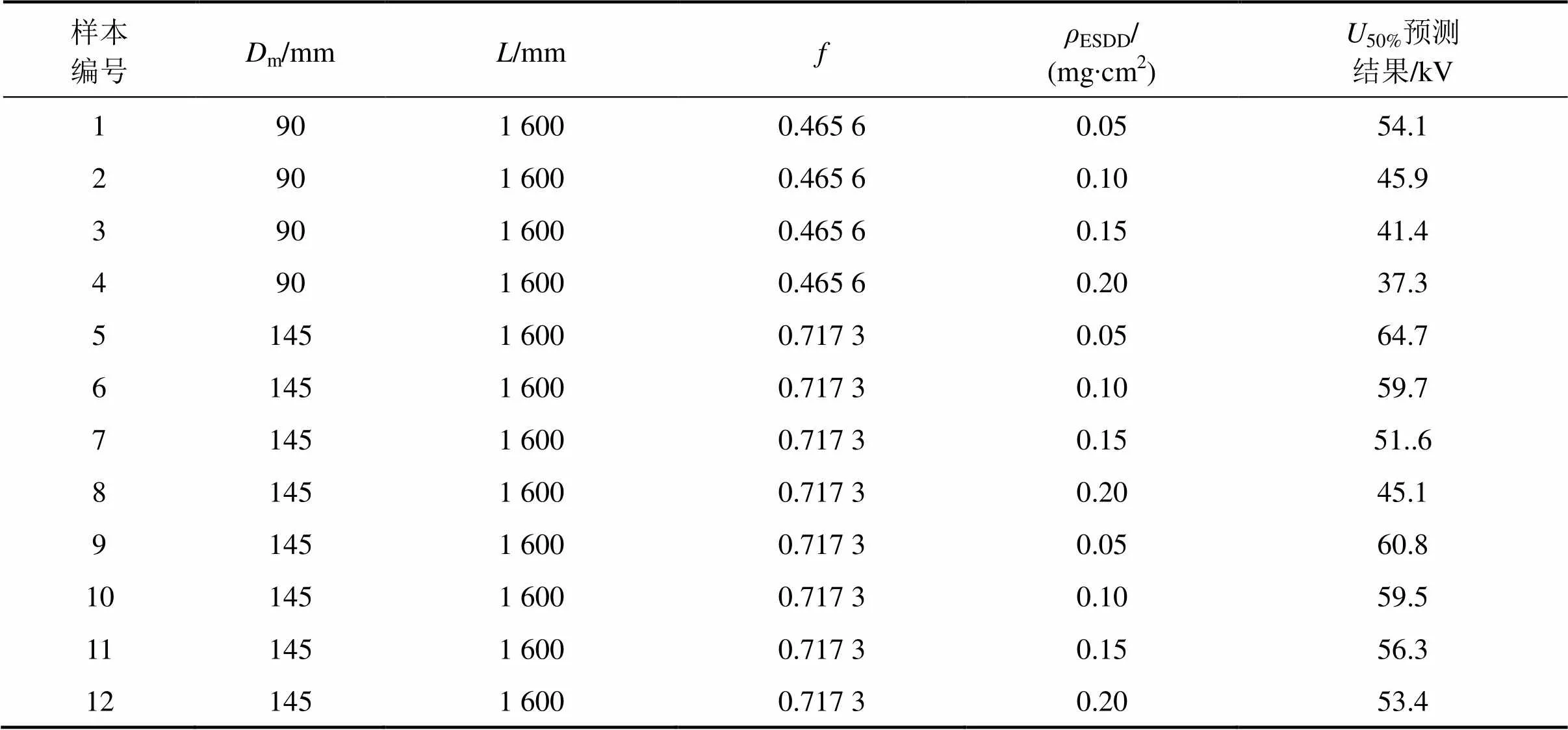
表4 临界污闪电压预测结果

分别运用本文所提方法、BBO算法优化BP神经网络、BP神经网络对复合绝缘子的临界污闪电压进行预测。将得到的临界污闪电压预测值与试验值进行比较，计算相对误差和平均相对误差(用Mean表示)，对比结果如表6所示。

从表6可看出，预测模型的优劣主要由预测性能来决定。本文所提方法的相对误差、平均相对误差几乎均比其余2种方法得出的结果要低，预测结果能更好的逼近试验结果，更有利于进行复合绝缘子临界污闪电压的预测。

表6 3种方法的相对误差与平均相对误差的比较

4 结论

1) 通过人工污秽试验取得大量试验数据，利用CS-BBO算法优化BP神经网络的方法对接触网复合绝缘子临界污闪电压、等值盐密及绝缘子自身参数之间关系进行建模。建立复合绝缘子临界污闪电压预测模型，实现了对接触网复合绝缘子临界污闪电压预测方法的初步探索，为评估接触网线路的可靠性以及对新建线路外绝缘的选型和维护提供了一条新的思路。

2) 接触网复合绝缘子种类繁多，对其进行临界污闪电压的试验研究花费的人力和物力很大，经济性不佳。通过复合绝缘子临界污闪电压预测模型得出的预测值可作为污闪试验的参考数据，能够有效降低污闪试验的工作量，提高接触网复合绝缘子污闪试验研究的效率。

[1] 裴升文, 支红强. 一起复合绝缘子污闪事故的原因分析及防范[J]. 电力安全技术, 2011, 13(1): 36−37. PEI Shengwen, ZHI Hongqiang. Analysis and prevention of the pollution flashover accident of the composite insulators[J]. Electric Safety Technology, 2011, 13(1): 36−37

[2] 叶汉欣. 污秽成分对复合绝缘子闪络特性的影响研究[D]. 重庆: 重庆大学, 2015. YE Hanxin. Influence of contamination composition on flashover characteristics of composite insulators[D]. Chongqing: Chongqing University, 2015.

[3] Kontargyri V T, Gialkestsi A A, Teskouras G J, et al. Design of an artificial neutral network for the estimation of the flashover voltage on insulator[J]. Electric Power System Research, 2007, 77(12): 1532−1540.

[4] 石岩, 蒋兴良. 基于RBF网络的覆冰绝缘子闪络电压预测模型[J]. 高电压技术, 2009, 35(3): 591−596. SHI Yan, JIANG Xingliang. Based on RBF network of ice covered insulators flashover voltage forecasting model[J]. High Voltage Engineering, 2009, 35(3): 591− 596.

[5] 舒立春, 白困利. 基于支持向量机的复杂环境条件下绝缘子闪络电压的预测[J]. 中国电机工程学报, 2006, 26(17): 127−131. SHU Lichun, BAI Kunli. Prediction of insulator flashover voltage under complex environmental conditions based on support vector machine[J]. Proceedings of the Chinese Society of Electrical Engineering, 2006, 26(17): 127− 131.

[6] 丁龙, 郝虎在. 基于支持向量机回归法的绝缘子污闪电压预测研究[J]. 电瓷避雷器, 2014, 16(1): 23−25. DING Long, HAO Huzai. Prediction of insulator pollution flashover voltage based on support vector machine (SVM) [J]. Insulators and Surge Arresters, 2014, 16(1): 23−25.

[7] Shewehdi M H, Farag A S, Izzularab M A. Estimating the insulation strength of two series non-ceramic dielectrics on distribution systems a statistical approach[C]// Electrical Insulation Conference, Rosemont, 1997: 799− 804.

[8] Kiruthika M, Sivadasan J. Evaluation and prediction of flashover voltage on contaminated composite insulators [C]// Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, 2015(2): 978−982.

[9] Boussaid I, Chatterjee A, Siarry P, et al. Two-stage update biogeography-based optimization using differential evolution algorithm[J]. Computer and Operations Research, 2011, 38(8): 1188−1198.

[10] Bhattacharya A, Chattopadhyay P K. Hybrid differential evolution with biogeography-based optimization for solution of economic load dispatch[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1955−1964.

[11] 黄成才, 李永刚. 基于复合绝缘子污闪模型的闪络特性分析[J]. 电瓷避雷器, 2014, 16(4): 31−36. HUANG Chengcai, LI Yonggang. Based on composite insulator pollution flashover model of flashover characteristics analysis[J]. Insulators and Surge Arresters, 2014, 16(4): 31−36.

[12] 王秀娟, 王刚. 染污情况下硅橡胶表面直流电弧特性研究[J]. 电瓷避雷器, 2015, 12(6): 31−38. WANG Xiujuan, WANG Gang. Contamination conditions of silicon rubber surface DC arc characteristics[J]. Insulators and Surge Arresters, 2015, 12(6): 31−38.

[13] 胡琴, 殷攀程. 交流工作电压下染污方式对220 kV复合绝缘子覆冰及闪络特性的影响[J]. 中国电机工程学报, 2015, 35(18): 4817−4824. HU Qin, YIN Pancheng. Stain mode under AC voltage of 220 kV composite insulator icing and flashover characteristics[J]. The Chinese Journal of Electrical Engineering, 2015, 35(18): 4817−4824.

[14] 方春华, 周毅. 基于泄漏电流相位差的绝缘子污秽度表征方法研究[J]. 高压电器, 2016, 52(2): 7−12. FANG Chunhua, ZHOU Yi. Study on the insulator contamination degree representation method based on the phase difference of leakage current[J]. High Voltage Electrical Apparatus, 2016, 52(2): 7−12.

[15] 黎鹏, 黄道春. 加压方式对山火条件下间隙击穿特性的影响研究[J]. 电网技术, 2016, 40(5): 1576−1581. LI Peng, HUANG Daochun. Effect of pressure on the breakdown characteristics of gap under fire conditions on[J]. Power System Technology, 2016, 40(5): 1576− 1581.

(编辑 蒋学东)

Research on prediction method of flashover voltage of composite insulators of contact network

WANG Sihua1, CAO Liming1, JING Hong2

(1. School of Automation & Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. State Grid Pingliang Power Supply Company, Pingliang 744000, China)

11 kinds of composite insulators commonly used by the contact network undergo a series of pollution flashover experiments in the artificial fog cabinet. Following that, a critical pollution flashover voltage prediction model of composite insulators of the contact network was proposed based on optimization of BP neural networks and an improved biogeographic algorithm was put forward. Cap diameterm, creep distance, form factor, and equivalent salt deposit density, ESDD, were adopted as input characteristic quantities of the model. Experimental and comparative analysis results suggest the model’s prediction effect is favorable, and that prediction results basically coincide with experimental results. The prediction value can be adopted as the referential data of the flashover experiment and can efficiently reduce the workload of the pollution flashover experiment. This research can provide a new perspective for reliability evaluation of contact network lines and model selection and maintenance of external insulation of newly-built lines.

composite insulator; pollution flashover; contamination test; critical flashover voltage prediction; biological geography algorithm; BP neural network

10.19713/j.cnki.43−1423/u.2018.08.023

TM216

A

1672 − 7029(2018)08 − 2083 − 09

2017−05−19

国家自然科学基金资助项目(51567014，51767014)；中国铁路总公司科技研究开发计划资助项目(2017010-C)

王思华(1968−)，男，江苏南通人，教授，从事高电压与绝缘技术方向研究；E−mail：503665230@qq.com