基于R软件的整群抽样案例教学方法

[摘 要]传统的抽样调查课程教学过于注重理论推导，缺乏实际应用，以至于学生在学习过程中未能真正掌握其中方法，不懂得如何运用所学的方法解决实际问题。课题组对实际抽样时整群抽样的抽样与估计步骤进行了系统的讲解，并结合R软件完成了整群抽样的样本抽取与总体参数估计。通过案例教学，帮助学生掌握整群抽样的理论知识，并提高了学生运用R软件解决实际问题的能力。

[关键词]案例教学；抽样调查；整群抽样；R软件

[中图分类号] G642 [文献标识码] A [文章编号] 2095-3437（2018）07-0065-03

○、引言

抽样调查作为一门应用性、实用性很强的统计学科，是统计学类专业的专业必修课程。然而，传统的抽样调查课程教学过于注重理论推导，缺乏实际应用，以至于学生在学习过程中未能真正掌握其中方法，不懂得如何运用所学的方法解决实际问题。为此，候震梅（2016）[1]探讨了抽样调查课程实验教学改革的思路与途徑；张学新（2015）[2]提出一种抽样调查课程贯穿统计软件使用的教学改革方法；卢玉桂（2015）[3]提出应运用案例教学法进行抽样调查课程教学。

整群抽样具有实施调查便利、节省费用的优点，因而被广泛应用于调查中。但笔者在教授该知识点时，发现大部分学生无法真正理解与掌握整群抽样方法。因此，笔者拟在前人研究基础[4][5]上，结合多年教授抽样调查课程的经验，探讨如何利用R软件帮助学生更好的理解与掌握“整群抽样”抽样与估计过程。

一、整群抽样简介

整群抽样（cluster sampling）[5]是将总体划分为若干个群，然后以群为抽样单元，从总体N（总体群数）抽取n个样本群，并对样本群中的所有单元进行调查的一种抽样方法。整群抽样分为群规模相等和群规模不等两种情况。所谓群规模是指组成群的单元数量，群规模可大可小。群规模大，则估计精度差但费用省；群规模小，则可提高估计精度但费用也高。因此，一般而言，群规模不宜过大。本文主要介绍群规模相等的整群抽样（也称为等概率整群抽样），等概率整群抽样是指在总体N个群（初级抽样单元）中，每个群所包含的单元（二级单元）数皆等于M。

等概率整群抽样一般用简单随机抽样方法抽取群，此时抽样比为f=n / N，则总体均值[y]的无偏估计为：

二、群抽样的R软件实现

笔者在进行整群抽样教学时，发现多数学生学起来吃力，无法理解整群抽样与简单[?]随机抽样的关系，以至于产生厌学、不学等一些负面情绪。为了帮助学生更好的掌握整群抽样方法，笔者将通过文献[5]的例子，讲解整群抽样过程。

例 某邮局该辖区共有5000户，并划分为500个群，则每个群有10户居民。为了解邮局管辖区内每个家庭的月平均定报份数及其95%的置信区间，运用整群抽样方法从500个群中抽取5个群进行抽样调查。

本例中，每个群的规模均为10，故为等概率整群抽样。因此，抽样方法为运用简单随机抽样从500个群中抽取5个群。因为是按照简单随机抽样抽取群的，所以每个群的入样概率均为5/500=1/100，又因为总体中的某个群一旦被抽中，则群内的所有单元全部入样。因此，每个总体单元的入样概率都为1/100，这也验证了群规模相等的整群抽样为何也可称为等概率整群抽样。

实施抽样调查时，抽样与估计是分开进行的，且先抽样后估计。整群抽样的抽样步骤可分为以下两步：

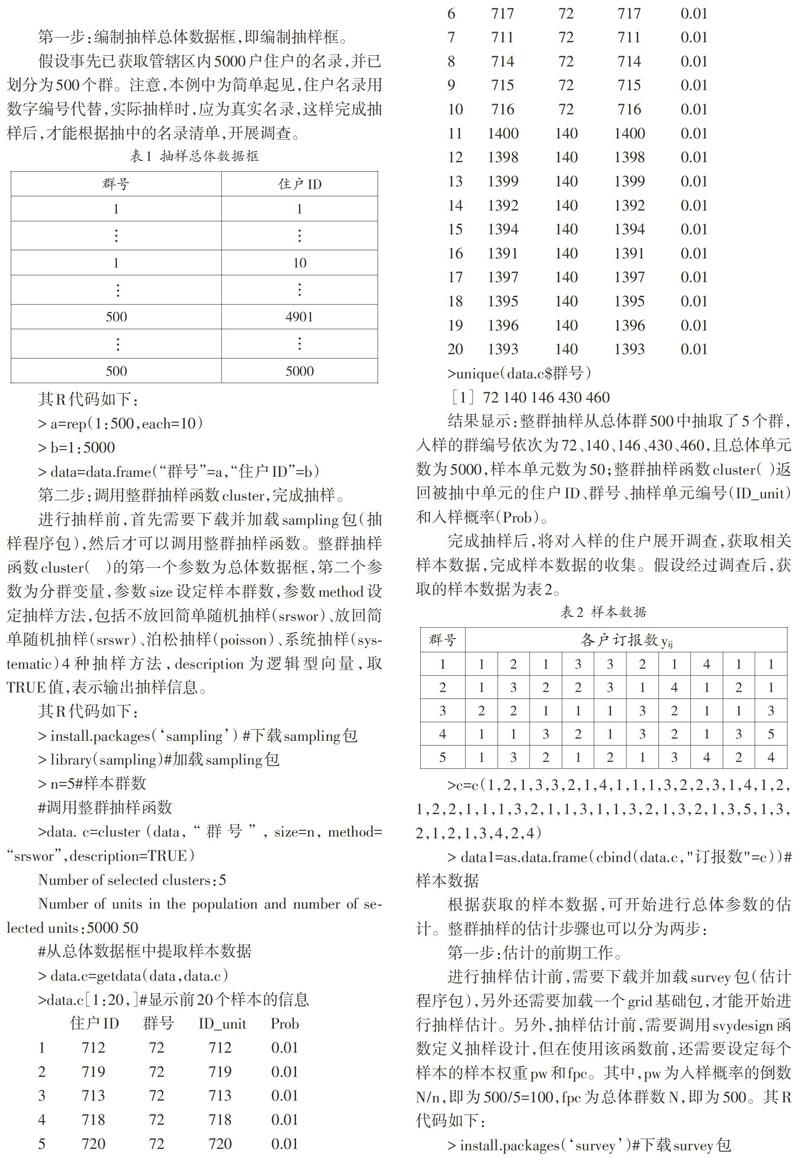
第一步：编制抽样总体数据框，即编制抽样框。

假设事先已获取管辖区内5000户住户的名录，并已划分为500个群。注意，本例中为简单起见，住户名录用数字编号代替，实际抽样时，应为真实名录，这样完成抽样后，才能根据抽中的名录清单，开展调查。

其R代码如下：

> a=rep（1：500，each=10）

> b=1：5000

> data=data.frame（“群号”=a，“住户ID”=b）

第二步：调用整群抽样函数cluster，完成抽样。

进行抽样前，首先需要下载并加载sampling包（抽样程序包），然后才可以调用整群抽样函数。整群抽样函数cluster（ ）的第一个参数为总体数据框，第二个参数为分群变量，参数size设定样本群数，参数method设定抽样方法，包括不放回简单随机抽样（srswor）、放回简单随机抽样（srswr）、泊松抽样（poisson）、系统抽样（systematic）4种抽样方法，description为逻辑型向量，取TRUE值，表示输出抽样信息。

其R代码如下：

> install.packages（‘sampling） #下载sampling包

> library（sampling）#加载sampling包

> n=5#样本群数

#调用整群抽样函数

>data.c=cluster（data，“群号”，size=n，method=“srswor”，description=TRUE）

Number of selected clusters：5

Number of units in the population and number of selected units：5000 50

#从总体数据框中提取样本数据

> data.c=getdata（data，data.c）

>data.c[1：20，]#显示前20个样本的信息

结果显示：整群抽样从总体群500中抽取了5个群，入样的群编号依次为72、140、146、430、460，且总体单元数为5000，样本单元数为50；整群抽样函数cluster（ ）返回被抽中单元的住户ID、群号、抽样单元编号（ID_unit）和入样概率（Prob）。

完成抽样后，将对入样的住户展开调查，获取相关样本数据，完成样本数据的收集。假设经过调查后，获取的样本数据为表2。

根据获取的样本数据，可开始进行总体参数的估计。整群抽样的估计步骤也可以分为两步：

第一步：估计的前期工作。

进行抽样估计前，需要下载并加载survey包（估计程序包），另外还需要加载一个grid基础包，才能开始进行抽样估计。另外，抽样估计前，需要调用svydesign函数定义抽样设计，但在使用该函数前，还需要设定每个样本的样本权重pw和fpc。其中，pw为入样概率的倒数N/n，即为500/5=100，fpc为总体群数N，即为500。其R代码如下：

> install.packages（‘survey）#下载survey包

> library（survey） #加载survey包

> library（grid）#加载grid包

> N=500#设定总体群数

> n=5#设定样本群数

> pw=rep（N/n，nrow（data1））#设定样本权重

> fpc=rep（N，nrow（data1））#设定fpc变量

> data1.c=as.data.frame（cbind（data1，pw，fpc））#合并样本数据框

> data1.c[1：5，]#显示前5行样本数据框

第二步：调用svydesign函数定义抽样设计，并完成估计。抽样设计函数svydesign（ ）参数id定义群变量，参数weights定义样本权重，参数data定义样本数据框，参数fpc定义fpc变量。

> d.c<-svydesign（id=～群号，weights=～pw，data=data1.c，fpc=～fpc）#抽样设计

> summary（d.c）#查看抽样设计

1 - level Cluster Sampling design

With （5） clusters.

svydesign（id = ～群号，weights = ～pw，data = data1.c，fpc = ～fpc）

Probabilities：

Min. 1st Qu. Median Mean 3rd Qu. Max.

0.01 0.01 0.01 0.01 0.01 0.01

Population size （PSUs）：500

Data variables：

[1] “住戶ID”“群号”“ID_unit”“Prob”“订报数” “pw”“fpc”

> svymean（～订报数，d.c）#订报数的均值估计和标准误差

mean SE

订报数 2.02 0.1062

结果显示：订报数的均值估计值为2.02份，标准误差为0.1062，则订报数的均值估计值的95%置信区间为[1.8119，2.2282]。

三、结论

本文以一个简单的抽样案例，对整群抽样的抽样与估计过程进行了系统的讲解，并结合R软件完成了整群抽样的抽样与估计。通过运用案例教学方法进行整群抽样的课堂教学，不仅可以帮助学生理解与掌握整群抽样的理论知识，同时还可以提高学生灵活运用R软件的能力，以及运用R软件解决实际抽样调查的能力。为此，在进行抽样调查课程教学时，应注意运用实际案例和R软件演示相结合进行教学，这将有利于学生对抽样理论知识理解与掌握，同时提高学生运用R软件解决实际问题的能力。

[ 参 考 文 献 ]

[1] 侯震梅. 《抽样调查》实验教学创新性研究[J]. 现代商贸工业，2016（10）：168-169.

[2] 张学新. 《抽样调查》课程的统计软件教学方法实践[J]. 宁夏师范学院学报，2015（6）：83-91.

[3] 卢玉桂. 案例教学法在《抽样调查》课程教学中的应用[J]. 亚太教育，2015（4）：104+93.

[4] 王伟，陈志军，徐辰武. 基于R语言的随机抽样方法及其应用[J]. 扬州大学学报（农业与生命科学版），2014（2）：77-81.

[5] 金勇进等.抽样技术：第四版[M].北京：中国人民大学出版社，2015.

[责任编辑：林志恒]