动态测量的高光谱图像压缩感知
闫 歌,许廷发,马 旭,张宇寒,王 茜,谭翠媚
(北京理工大学 光电学院 光电成像技术与系统教育部重点实验室,北京 100081)
1 引 言
高光谱遥感成像可同时获取高空间分辨率和高光谱分辨率的图像,在矿物勘探、环境监测和食品检测等方面有着广泛的应用[1-6]。由于应用面广,高光谱成像设备的发展十分迅速,逐渐朝着轻便小型化的方向发展[7-8]。但高光谱图像空间分辨率、光谱分辨率的不断提高,导致图像数据量成倍增加,给数据的存储和传输增加了压力,限制了高光谱成像技术的进一步发展。因此,如何有效地压缩高光谱图像是当前该领域的研究热点。
压缩感知(Compressive Sensing,CS)理论指出,如果信号在某一变换域是 K-稀疏的或者说是可压缩的,那么可以设计一个与相变换基不相关的测量矩阵来对信号进行观测。其可利用低维测量值,通过求解一个凸的最优化问题来实现原始信号的重构[9-10]。CS边压缩边采样的特性,相对于传统数据传输省去了先获得大量冗余数据再压缩的麻烦,降低了采样成本,减少采样时间。CS主要分为信号压缩感知测量和信号重构两个步骤,在压缩过程中运算量较少,而重构则需要经过大量运算多次迭代获得最优解。因此大多数压缩感知算法的研究重点都在重构算法方面[11-13]。常见的重构算法有凸优化算法、贪婪算法等,其中凸优化算法重构精度高但计算量大,贪婪算法计算量小但重构精度低。影响信号恢复的质量除了重构算法外还有其他因素,例如能否找到合适的稀疏基对信号进行稀疏表示、观测矩阵能否在采集过程中保留大部分原始信号的信息,以及能否在压缩测量过程中合理地分配采样率等。在视频压缩感知(Compressive Video Sensing)中,由于图像规模较大,需要先进行分块,然后分别对每一个图像块进行压缩测量。针对这一问题,已经有不少学者提出了自适应采样的方案,例如文献[14]利用图像块方差作为衡量细节复杂度的参数,为各块设定不同的测量率,但由于不同的图像方差块差距可能巨大,导致分配的测量值差距也很大,甚至有可能出现采样值超出图像块像素数的情况;Hung-Wei Chen等人[15]利用前一帧图像作为参考帧,训练出图像的稀疏字典,通过训练出的稀疏字典对参考帧进行稀疏表示,再根据图像块稀疏表示后的稀疏系数的方差自适应分配采样率。但假如图像使用普通稀疏基(如DCT基,小波基等)来稀疏表示,不训练稀疏字典的情况下,得到的各图像稀疏系数方差的差距很大,并不能合理分配测量值;左觅文等人[16]提出了一种基于帧间相关性的自适应采样率分配方案,将图像块采样分为固定预采样、基于图像块复杂度比例的自适应采样两个采样部分,根据图像块的变化程度动态调整测量率。上述方案都是基于视频信号的帧间相关性很高这一特性来进行自适应采样的。高光谱图像相邻波段间的相关性也很高,目前的利用高光谱图像光谱相关性的研究主要在谱间预测重构研究方面[17-18],并且目前的高光谱压缩感知算法普遍以固定的测量率对每个波段的图像块进行测量[19]。用高光谱图像强谱间相关性,可以将自适应采样率应用在高光谱图像压缩感知领域。另外,由于目前高光谱压缩感知成像系统只能同时对所有图像块采集相同测量值,上述的自适应测量方法虽然提高了图像的重构精度,但是由于存在方差悬殊等问题,导致不同图像块分配的测量值数目也相差很大,这对自适应压缩感知算法应用于高光谱成像系统带来了困难。
本文提出一种利用边缘信息动态测量高光谱图像的压缩感知算法。该方法有效利用高光谱图像波段间的相关性,根据各波段图像块含有边缘信息的多少自适应地调整测量率,在给定总采样率的条件下可实现图像块的采样率动态分配。由于在背景区域对每个图像块都给定了最少的测量值数目,因此既不会牺牲背景的重构效果,又控制了图像块间测量值数目差异,使自适应压缩感知理论应用在系统中成为可能。
2 动态测量的高光谱图像压缩感知
为了获得边缘信息,就要先获取原始信号。基于高光谱图像谱间相关性很高的特性,可以先用传统压缩感知方法用固定测量率的随机矩阵对某个波段先进行观测,获得测量值后重构出该波段图像,作为其他波段的先验信息。本文提出的利用边缘信息的动态测量压缩感知高光谱图像重构算法框架,如图1所示。在该框架中,对参考波段采用传统的固定采样率测量,然后重构出参考波段的图像,获得图像的先验信息后,再对非参考波段图像采用本文提出的动态测量率进行采样与压缩感知重构。
在对参考波段图像进行测量时,每个图像块的测量率是固定的,通过传统压缩感知方法测量并重构出图像后,对该图像进行边缘提取,获得边缘信息。由于高光谱图像谱间相关性很高,并且图像在空间方向上是不移动的,那么提取的边缘区域就可以看作是所有波段的边缘区域。有了高光谱图像的边缘信息后,就可以根据待测量的图像块中含有边缘信息的多少来分配测量值,含有边缘信息多的图像块分配的采样率高,含有边缘信息少的图像块分配的采样率低。

图1 利用边缘信息的动态测量压缩感知高光谱图像重构算法 Fig.1 CS hyperspectral image reconstruction algorithm based on edge information
2.1 高光谱图像参考波段的观测
对高光谱图像参考波段的观测是采用固定测量率的分块压缩感知方法。参考波段Nr×Nc个像素的图像Xkey包含了n个大小为B×B的不重叠块,第i个图像块的列向量表示为xi,i=1,2,…,n,通过对每个图像块用相同的随机投影矩阵观测,可以得到第i个图像块的压缩测量值
yi=Φxi,
(1)
式中,Φ是一个大小为M×B2的测量矩阵,M为测量次数,并有M< R=M/B2, (2) 参考波段的重构图像将用来提取边缘区域,然后利用边缘信息作为分配动态测量率的重要参数。参考波段的重构质量将影响边缘提取的准确性,从而影响整个高光谱图像的重构效果。所以,参考波段会采用较高的采样率进行压缩观测,以保证重构出的图像质量良好。 2.2.1 提取边缘区域 (3) 式中,x、y分别对应图像的横轴方向和纵轴方向。接下来要计算平滑后的图像I中每个像素点的梯度值和对应的方向,先用一阶微分算子分别得到点(i,j)两个方向的偏导数Gx(i,j)和Gy(i,j),那么图像I中像素点的梯度幅值G(i,j)和梯度方向θ(i,j)分别为: (4) (5) 计算出全局的梯度仍然不能确定图像边缘,为达到细化梯度幅值图像的目的,要进行极大值抑制处理,只保留梯度值的局部最大点。在图像中以点(i,j)为中心的邻域中沿梯度方向θ(i,j)进行插值,若点(i,j)处的梯度值大于相邻插值点,则(i,j)为图像梯度中的局部最大点,反之则为非局部极大值点,设置非局部极大值的点为0,最终得到细化后的图像。 细化后的图像是候选的图像边缘及边缘线段,需要继续筛选并连接出最终的图像边缘。Canny算法使用双阈值法实现边缘的检测与连接。分别设置好一个高阈值和一个低阈值对细化后的图像中记为局部最大值的点进行检测,高于高阈值的点则为边缘点,低于低阈值的点记为非边缘点,处于两阈值之间的点记为候选边缘点,结合已确定为边缘点的信息及连通性,若候选边缘点临近像素中已有边缘点,则该候选边缘点记为边缘点,否则从候选边缘点中去除。 用Canny算法提取出图像边缘后,需要划分出图像边缘区域,确定哪些区域包含边缘信息。为了更快速地划分出图像边缘区域,本文使用图像膨胀算法以将提取出的细化图像边缘增强扩展并划分出图像边缘区域。具体操作为:将边缘图像与结构元素进行卷积,本文使用大小为b×b的元素都为1的矩阵作为结构元素,计算结构元素在边缘图像中覆盖区域像素点的最大值,并把这个最大值赋给结构元素所覆盖的区域,这样就使边缘膨胀加粗,最后得到记录边缘区域的图像IE。 2.2.2 动态测量率设定方法 记录边缘区域的图像IE是二值化图像,值为1的像素点代表属于边缘区域,值为0的像素点代表属于背景区域。在设定动态测量率之前,首先要对记录边缘区域的图像分块,文中利用对高光谱图像分块的方法对IE进行分块,得到n个大小为B×B的不重叠块,这样分块后可以使高光谱图像中的图像块和IE中的块互相对应。接着计算每个图像块的像素点灰度值的总和S,第i块的值记为Si,i=1,2,…,n,从而可以由S值知道每个图像块包含多少边缘信息,S值高的图像块包含的边缘信息多,S值低的图像块包含的边缘信息少,S=0的块不含边缘信息即属于背景区域。由于IE和高光谱分块图像的各个区域一一对应,那么可知图像块xi对应的边缘信息值为Si。 在总测量值数目固定的条件下,需要对边缘信息多的区域多采样、背景区域少采样从而达到提高图像重构质量、优化图像细节的目的,即图像块的S值高,则该图像块的采样率高,测量值的长度M大。本文建立一个线性模型将第i图像块的S值映射到测量值的长度,记Mi为第i个图像块要采集的测量值个数,那么映射关系如下: Mi=kSi+m, (6) 式中,k为待计算的比例系数,m为背景区域固定测量数目,m值的大小与总测量率、图像块像素数有关,设定要求为在不影响图像整体重构质量的前提下使m值尽可能小。这个值可以在采集数据前根据经验值提前设定好。由于图像包含了n个大小相同的图像块,那么每块的测量值个数如式(7)所示: M1=kS1+m, M2=kS2+m, ⋮ Mn=kSn+m. (7) 将上式等号左右两边分别全部相加,得到 (8) (9) 将等式(9)中比例系数k的值代入边缘信息与图像块测量值数目的映射关系式(6)中,则就可以利用边缘信息得到每个图像块不同的自适应测量值数目,则第i个图像块最终的动态测量值数目为Mi: (10) 式中,round(·)表示对括号内的计算结果四舍五入取整数。 对非参考波段的动态测量率自适应采样流程如图2所示。 高光谱图像利用边缘信息进行动态测量的具体实施流程如下: 步骤1:将高光谱图像的每个波段都分成n个大小为B×B的不重叠图像块; 步骤2:对参考波段的图像按照固定采样率采集,其采样率比非参考波段设置的稍高一些,这样可以保证参考波段的重构质量,从而使非参考波段自适应分配更合理准确; 步骤3:将参考波段获得的观测数据用压缩感知算法重构出来,获得该波段的图像; 步骤4:对参考波段重构出的图像进行边缘提取,并用图像膨胀方法增强边缘,划分出图像边缘区域; 步骤5:提取的边缘区域图像也按照步骤1相同方法分成n个大小为B×B的不重叠图像块,计算每块内所有像素的灰度和,该值表示图像块含有的边缘信息量,记为Si,i=1,2,…,n; 步骤6:设定背景区域(不含边缘信息)的图像块的固定测量值数目m; 图2 非参考波段动态测量率的自适应采样流程图 Fig.2 Adaptive sampling flow chart of dynamic measurement rate in non-reference band 步骤7:根据公式(10)计算出每个图像块最终分配的自适应测量值数目。 在高光谱图像重构端,接收到各个波段图像的观测数据后,采用相同的压缩感知算法进行分块重构。 在高光谱压缩感知成像系统中,目前都是采用固定测量率的方式对图像进行采集,尤其在分块压缩感知中,由于每个图像块都是同时采集时,必然导致直接获取到的测量值数目相同。因此,动态分配测量值的压缩感知算法就很难在系统中实现。如果必须要在高光谱压缩感知系统中应用动态测量算法,那么在系统中设定的采集测量率则不能小于所有图像块中最大测量率的值,即每个图像块采集次数为M≥max{Mi},其中Mi是由式(10)计算出的每个图像块分配的测量值数目。这样才能保证每个图像块都获取到所需的动态测量值数量。 由于高光谱数据为三维数据,既有二维空间信息,又有很高的光谱分辨率,使得高光谱图像数据量庞大。为了减小数据传输的压力,同时又保证图像质量,可以在采集一定数量的观测数据后丢掉一些冗余信息来缓解数据传输压力。在这种情况下,可以采用自适应采样率分配的算法来选择保留不同图像块的观测值数量。但由于传统的自适应测量率方法是根据图像块的方差大小分配测量率的,不同图像纹理信息不同,极有可能造成图像方差相差悬殊,导致不同图像块分配的测量值数目差异也非常大,最大分配数量甚至有可能超过图像块本身的像素数。而本文提出的利用边缘信息动态测量高光谱图像的方法中,对背景图像块也设置了固定测量值数目,并且按照图像块含有边缘信息的多少来进行分配,从而可以避免某些图像块分配测量值数目过大的情况。 本文对空间分辨率为256 pixel×256 pixel个像素,24个波段,波长为452~667 nm的Lego高光谱图像进行仿真实验。为了更准确地分配非参考波段的测量值数目,要选择一个边缘信息比较明显的波段作为参考波段。这里选择Lego高光谱图像的第9波段作为参考波段优先重构。图像分块过程中,每块的大小设置为8×8,参考波段的采样率设置为0.5,用离散余弦基(DCT)作为稀疏矩阵,采用SpaRSA压缩感知[8]算法独立地重构出各图像块。所有仿真实验都在相同的计算平台(Intel i5-4590 CPU 3.30 GHz /6.00 GB内存)下进行。 图3为参考波段采用固定测量率R=0.5时的重构结果,使用的观测矩阵为随机01分布的矩阵,矩阵中0和1的比例为1∶1,SpaRSA算法中的参数值设为0.01。重构出的图像与原图相比峰值信噪比(Peak Signal to Noise Radio,PSNR)为29.75 dB。 图3 参考波段重构图像 Fig.3 Reconstructed image of key band 将重构出的图像作为先验信息提取边缘区域。下图为对重构后的参考波段图像用Canny算子提取边缘,并用5×5的结构元素进行图像边缘膨胀后划分出的图像边缘区域。 图4 参考波段的边缘区域划分 Fig.4 Edge region extraction of key band 根据参考波段提取的边缘信息,接下来要对非参考波段分配动态测量值数目。其中,有两个参数可以根据经验值设置,分别为边缘膨胀的宽度b,以及背景区域图像块(不含边缘信息)的固定测量值m。下面以重构第10波段为例,分析这两个参数对动态测量算法重构效果的影响。这里图像总采样率设为0.3,使用的观测矩阵为随机01分布的矩阵,矩阵中0和1的比例为1∶1,SpaRSA算法中的参数τ值设为0.01。由于观测矩阵具有随机性,每组实验重构图像的PSNR值与重构时间(s)均取5次测试的平均值。 总采样率R=0.3,背景区域图像块m=5时,随着边缘膨胀宽度b的变化,第10波段的重构质量和重构时间数值如表1所示。 表1 m=5时重构结果 从表1可以看出,边缘膨胀宽度b对重构效果有影响,但是影响不很大,然而边缘膨胀宽度b不能设置过大,超过5之后,PSNR有明显下降趋势,另外随着b值增大,重构时间逐渐增长。综合表中结果来看,b=3是一个合适的边缘膨胀宽度值。 接下来分析背景区域图像块的固定测量值m对重构结果的影响。表2是总采样率R=0.3,b=3时,第10波段的重构质量和重构时间随m值变化情况。可以看出随着固定测量值m的增大,图像总体重构效果稍稍变差,重构时间增大。但是需要强调的一点是,在m=2时,许多图像块重构失败,所以固定测量值m值设定不能太小。m值设定过小时,虽然总体重构质量提高了,但是图像会出现局部失真情况。另外,背景区域测量值m也与图像总采样数量有关,总采样值高时m值也需要设置的相对高一些,避免图像局部重构效果过于失真。本文根据m=round(0.25·R·B2)来确定m的值,若计算出m<3时,m值设置为3。 基于上述参数设置分析结果,本文对Lego高 表2 b=3时重构结果 光谱图像中除第9波段外进行非参考波段重构的仿真实验。非参考波段的采样率分别设置为0.1、0.2、0.3、0.4、0.5,边缘膨胀宽度b=3,背景区域固定测量值m=round(0.25·R·B2),表3与图5为本文方法与传统固定测量高光谱图像的重构结果比较,图中结果为所有波段结果的平均值,并且每组实验重复5次取平均。 从表3和图5可以看出,本文提出的方法在总采样率较小(R=0.1)时,PSNR提高了1 dB,但是重构时间超过传统固定测量值的方法。这是由于总采样率过小的情况下,部分图像块无法获得充足的测量次数,导致图像质量提升不显著。但是在采样率R大于0.1之后,利用边缘信息动态测量的方法能显著提升图像质量,PSNR增益为3~4 dB时,因为图像边缘区域获得了足够的测量以后,在图像细节处图像质量改善明显,随着采样率增大,本文提出方法的重构时间也逐渐减小。 表3 非参考波段重构PSNR(dB)对比 图5 非参考波段重构结果比较 Fig.5 Reconstruction results comparison for non-key bands 图6给出了R=0.3,边缘膨胀宽度b=3,背景区域固定测量值m=round(0.25·R·B2)时的测量值数目分配情况。其中单个图像块的测量值数目分配最大值为59,小于图像块像素数B2=64,所以在真实高光谱压缩感知系统中可以实现。 图6 测量值数目分配情况 Fig.6 Allocation of the number of measurements 图7 第10波段重构结果比较 Fig.7 Reconstruction results comparison for band 10 图7是第10波段R=0.3时重构效果对比图,可以看到本文方法中玩偶的眼睛,衣服上的图案等图像细节处纹理清晰。可见本文利用边缘信息来分配采样率的方法是有效的,提高了图像的重构质量。 本文根据高光谱图像谱间相关性很强的特点,提出了利用边缘信息动态测量高光谱图像的压缩感知方法,通过根据图像块含有边缘信息的多少自适应分配采样率,讨论了动态测量方法在高光谱成像系统中实现的可行性。仿真结果表明,在总测量数目固定的条件下,采用本文提出的动态测量图像块方法重构出的图像比现有固定图像块采样率采样方法的质量更高,PSNR比传统方法高出1~4 dB图像细节处更清晰。下一步的工作重点将研究如何进一步合理分配测量值数目并将其成功应用于真实高光谱压缩感知系统。2.2 非参考波段的动态测量率观测


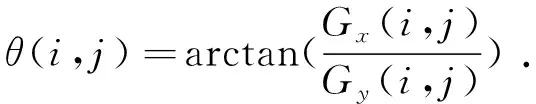

3 利用边缘信息进行动态测量流程
3.1 实施流程

3.2 动态测量实施的可能性讨论
4 实验结果与分析








5 结 论

