基于单次傅里叶变换的分段衍射算法

胡 琪，王 喆，刘洪顺，薛智文，邓家春

(天津理工大学 理学院，天津 300384)

1 引 言

计算全息是在实验全息术的基础上发展起来的，利用惠更斯-菲涅尔衍射原理，通过对光场衍射行为的数值计算，可模拟光场在各种光学系统中的衍射行为。由于不受实验环境因素的影响，这种分析方法具有较大的灵活性，经常用来做复杂系统实验的仿真模拟。随着光场测量技术的不断进步，计算全息在光场调控、光通讯、激光技术、衍射元件设计、光学系统开发等领域迸发出了巨大的活力[1-7]。在波前传感器[8-11]取得巨大进步的今天，人们开始尝试利用对物光波前的相位数据进行采集，并计算其通过光学成像系统后的成像结果，从而获得层析图像、深度图像或者三维立体图像，这些工作的开展都离不开较长距离衍射的精确计算[12-17]。因此，优化较长距离的衍射算法，具有很大的研究价值。本文依据采样定理[18]中对传输距离和衍射面画幅尺寸的关系，提出了一种分段衍射算法，解决传输距离对衍射面画幅尺寸和有效像素分辨率的影响，使算法可以灵活调整衍射面画幅尺寸。数据显示，计算结果与传统算法结果一致，而分辨率可提高2～3个数量级。

2 基本理论

在利用菲涅尔衍射积分计算光场衍射行为的过程中，单次快速傅里叶变换算法(Single Fast Fourier Transform Algorithm，S-FFT)在衍射距离较长的情况下表现出失真率低、计算速度快、抗欠采样性较强、内存使用少等诸多优势[19]。但是，由于采样定理的限制，此算法计算得到的衍射面画幅尺寸受衍射距离影响较大，特别是在传输距离较长的情况下出现画幅很大的情况，导致有效内容的像素分辨率很低，不利于分析有效数据和应用。本文基于采样定理分析了上述问题的产生原因，并提出了通过分割衍射距离的方法解决上述问题。模拟计算表明，该方法行之有效，并保留了S-FFT算法的优点。

根据惠更斯-菲涅尔原理，如图1所示，衍射面上P0处的光场U(P0)为从孔径S上各点发出的次级发散球面波exp(ikr01)/r01的相干叠加[9]。

(1)

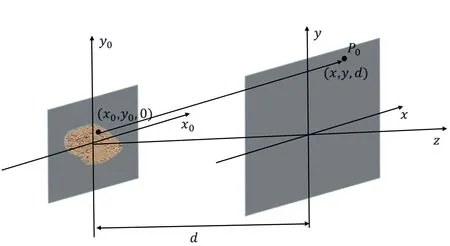
图1 在傍轴情况下衍射坐标示意图 Fig.1 Schematic diagram of diffraction coordinates in paraxial

利用标量衍射理论[20]，通过求解麦克斯韦方程[21-22]，并运用傍轴近似将积分简化，可以得到菲涅尔衍射积分的傅里叶变换形式[18]：

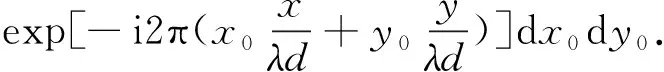
(2)

利用菲涅尔衍射积分，如图1所示，我们可以计算得到初始光场U(x0,y0,0)传播一段距离d之后等到的光场U(x,y,d)。

式(2)中设U(x0,y0)为物光平面波复振幅，U(x,y)为衍射面光波复振幅，传播距离为d，则菲涅尔衍射积分可以表示为：

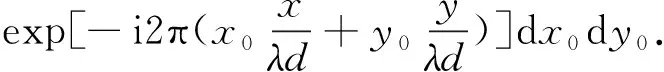
(3)

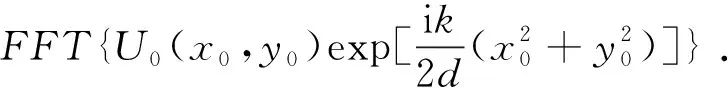
(4)

该算法称为S-FFT算法(single fast Fourier transform algorithm)[19-20]。由于仅运用了一次傅里叶变换，其计算速度和失真率均较低。

另外计算光场衍射行为较为常见的还有D-FFT算法(double fast Fourier transform algorithm)和T-FFT(triple fast Fourier transform algorithm)算法。经过实验比较，三种算法各有所长。其中D-FFT算法和T-FFT算法适用于较短距离衍射范围，其衍射面画幅尺寸等于初始画幅尺寸，二者之中D-FFT算法具有更强的抗欠采样性，而T-FFT算法则具有更强的衍射图案细节描绘能力。S-FFT算法更加适用于较长距离的衍射范围，弥补了另外两种算法在长距离上面的不足[19，23]。而本论文进一步优化了S-FFT算法在长距离衍射方面的表现出的衍射面画幅尺寸相比衍射图案过大、衍射图案分辨率低等缺点，为能够完满地获得整个菲涅尔衍射区域的衍射场做出了一点贡献。

3 采样定理对S-FFT算法中衍射面画幅尺寸的影响

下面讨论一下衍射面观察屏的最大坐标，以x轴方向为例。图2中绘制了单条光线在x-z平面中传播的过程，其传播方向为波矢k的方向，与x轴夹角为α。图中，x0轴为次级波源所在x-y平面的横轴坐标，x轴为衍射面观察屏所在平面的横轴坐标；虚线为光场的等阵面；光线从次级波源O点(x0=0,z=0)发出，传输到衍射面观察屏上的P点(x=x,z=d)。根据等阵面可知，光场在x方向的空间周期为X。

由图2可以得到光传播方向与空间频率的关系

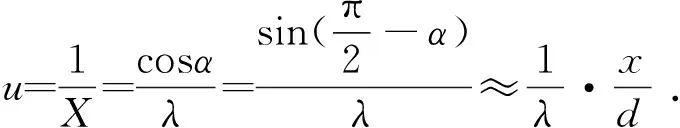
(5)

(6)

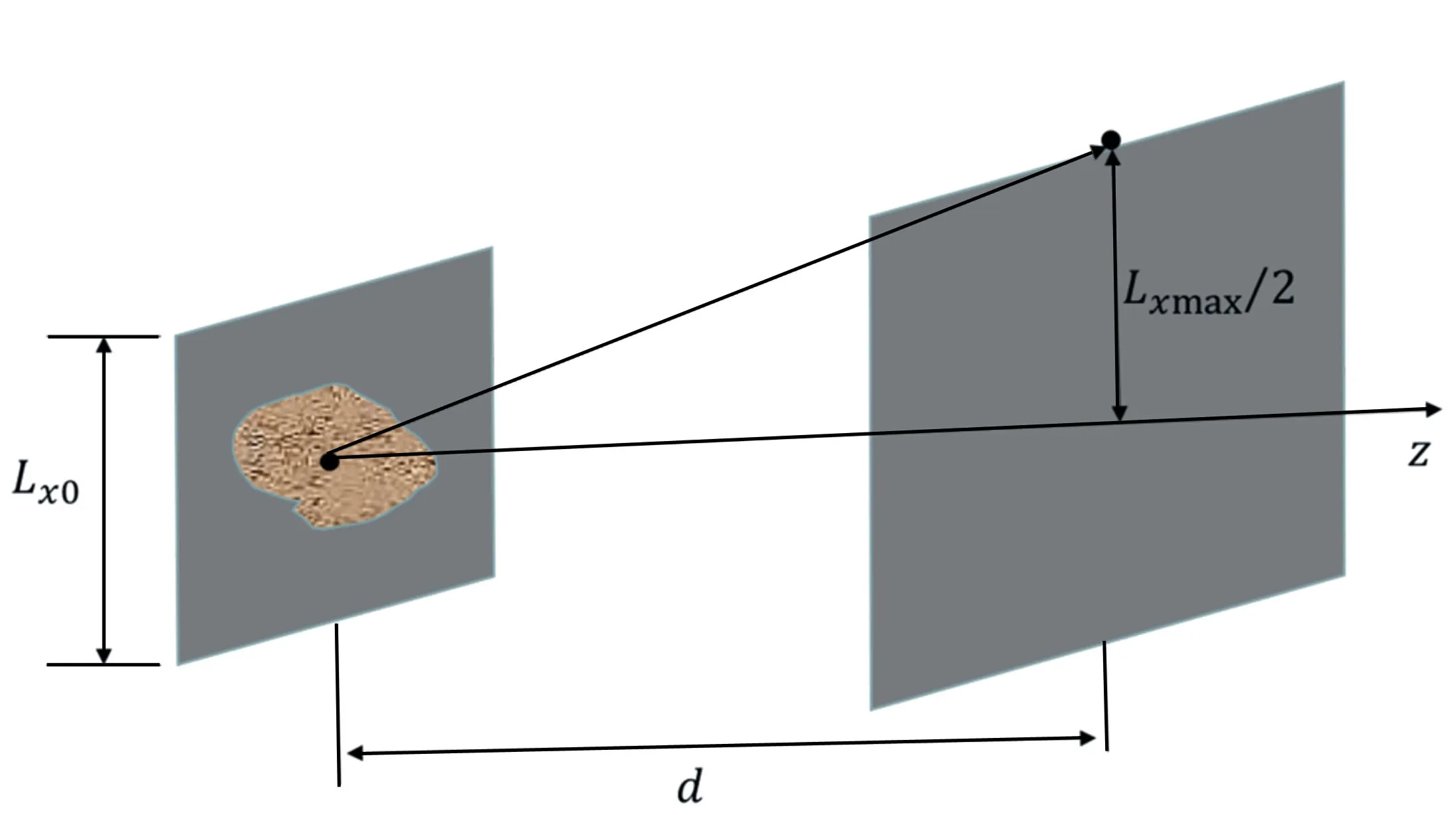
图3 衍射计算中衍射面观察屏再现范围示意图 Fig.3 Sketch map of viewing screen reproduction range in diffraction calculation

根据式(6)可以知，基于S-FFT算法计算衍射光路时，衍射观察屏的大小与采样数、光的波长、衍射距离以及初始衍射面大小(即衍射图案大小)4个因素相关。在实际中，由于波长、采样数、初始衍射面大小均由实验设备决定，衍射面观察屏的大小只与衍射距离有关，无法改变。当平行光照射物体，衍射距离过长时，衍射面画幅尺寸过大，会得到一个很小区域的衍射图像；当球面波照射物体，并使用凸透镜成像时，衍射距离过长会导致衍射面画幅尺寸过小，只能得到图像的某一个区域。这会使该算法在实际运用中，受到极大限制并严重影响图像中有效画面的像素质量。图5模拟计算了波长为532 nm的均匀平面光波垂直照射一个边长为5 mm的初始衍射面，中央开有边长为2.5 mm的正方形透光孔(如图4所示)后，经过不同距离d后在衍射面观察屏上的衍射光场及其光强分布。

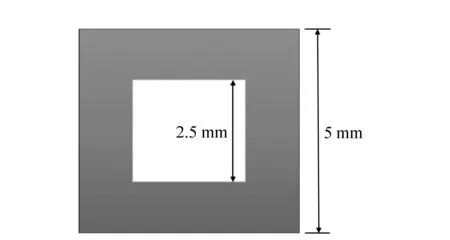
图4 程序模拟的透光孔 Fig.4 Transparent hole simulated by program

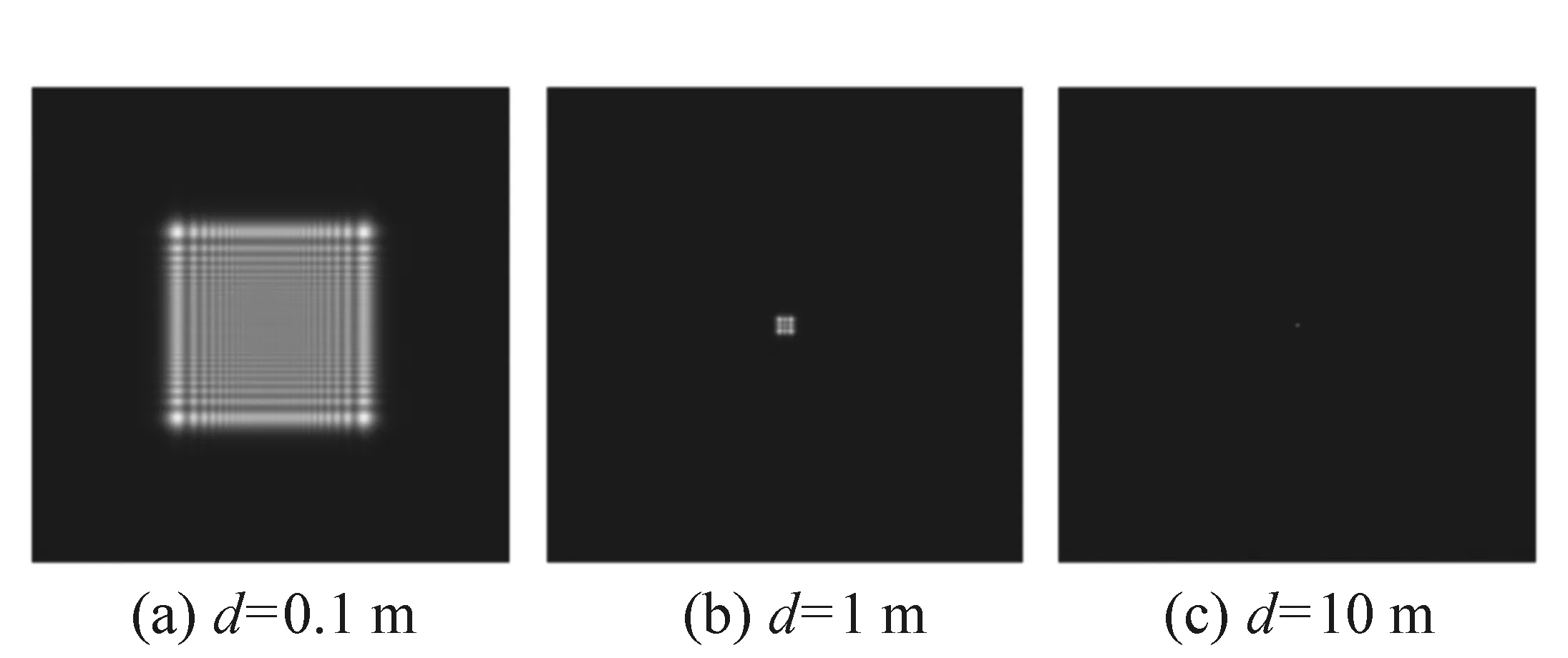
图5 在不同衍射距离下的衍射图样 Fig.5 Diffraction patterns at different diffraction distances

由图5可以看出，在默认初始衍射图案大小变化不大的情况下，随着衍射距离d的变化，衍射面画幅尺寸的区域变化很大。当衍射距离d过长时，衍射再现结果相比较衍射面画幅尺寸来说过小，很难观测。

为了解决上述问题，本文提出一种分段衍射算法。该方法是将衍射距离d划分为两段，分别记为d1、d2。这样，在每次衍射计算中，衍射面画幅尺寸在x和y方向的尺寸(Lx1、Ly1、Lx2、Ly2)都会因波长λ、采样数(M、N)、衍射距离(d1、d2)和初始衍射面大小(Lx0、Ly0、Lx1、Ly1)而改变。其中，衍射d1距离衍射面画幅尺寸为:

(7)

继续衍射d2距离的衍射面画幅尺寸为:

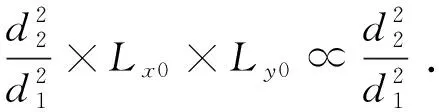
(8)

不难看出，衍射面画幅尺寸的决定因素就由d1，变成了d2/d1。

因此，该方法可有效、灵活的通过调整d1、d2的比值来控制最终衍射面画幅尺寸的大小，获得更高分辨率的有效像素数据，并保留S-FFT算法的高精度及低失真率。

4 模拟计算结果与分析

图6和图7分别计算了波长为532 nm的均匀平面光波垂直照射一个边长为5 mm中央开有边长为2.5 mm的正方形透光孔(如图4所示)的初始衍射面，经过d=1 m(图6)和d=10 m(图7)后，衍射面观察屏上的衍射光场及其光强分布。图中分别按照直接计算(图6(a)、图7(a))和分段衍射算法(图6(b)～(d)、图7(b)～7(d))计算得到的观察屏光强分布。

图6 衍射1 m后的衍射图像 Fig.6 Diffraction patterns after 1 meter of diffraction

图7 衍射10 m后的衍射图像 Fig.7 Diffraction patterns after 10 meters of diffraction

可以看出，分段衍射算法可以灵活有效的调整衍射面画幅尺寸大小，有效数据的分辨率得到了调控。在传输距离为1 m时，由于式(7)衍射面画幅大小为2 970.25 mm2，衍射图案占据的范围不到画幅范围的0.26%(以下简称“占比”)，有效内容像素只有676个。而利用分段衍射算法(以d1=d2=0.5 m为例)，根据式(8)可将画幅调整为25 mm2，使得衍射图案占据总画幅的43.58%，有效内容像素为114 244个，数据量增加了169倍。同样，在衍射距离为10 m时，传统S-FFT算法得到的衍射面画幅为296 807.04 mm2，其中有效像素仅为9个(占比0.34%)，而通过分段衍射算法(以d1=d2=5 m为例)实现的S-FFT算法得到的画幅为25 mm2，有效像素仍保持在154 449个(占比58.77%，数据量增加了17 285倍)，极大的提高了有效像素的数量。同时，通过表1和表2可知，其计算结果与传统算法保持一致。

表1和表2分别分析并统计了直接计算和分段衍射算法两种方法获得的衍射面画幅尺寸相应比例图像的失真度。其方法是(以d=1 m，d1=d2=0.5 m为例)首先根据衍射面画幅尺寸(直接计算的衍射屏边长为La=54.5 mm，分段衍射算法计算的衍射屏边长为Lb=5 mm)比例截取其中主要能量部分并作归一化(所有像素点数值除以像素中最大数值)，所得到图像作为对比图，把直接计算结果作为参考图，将对比图中的对应像素点做加权平均后形成一张与参考图像素个数相同(x像素数为M，y像素数为N)的比照图，然后用比照图fe(x,y)和参考图f(x,y)中的对应像素点数值对比计算均方根误差erms和峰值信噪比Rsn[24]。其计算方法为：

(9)

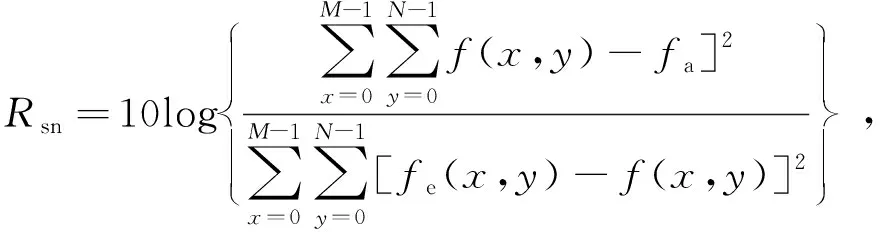
(10)

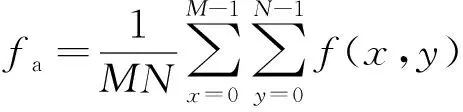
表1 衍射距离d=1 m时，直接计算与分段衍射算法计算图像的erms和Rsn

由表1可见，两幅图的均方根误差均小于0.1，而峰值信噪比均大于20，两幅图的保真度较高。其误差产生的主要原因，除了对应像素点个数不是整数之外，还应考虑到分辨率较高的对比图本身细节增多，其平均强度值与参考图中对应像素的数值理应存在一定偏差。这种偏差其实也反映了图像分辨率增加后导致图案细节增多。因此在一定程度上，本问题中分析失真度时，误差并非越小越好。

同样的，运用上述方法在表2中总结了衍射距离为10 m时，两种计算方法获得结果的均方根误差和峰值信噪比。从中可以看出，与d=1 m时结果类似，对照图和参考图相似度也很高。而由于在较长衍射距离的情况下，直接计算得到的衍射面画幅尺寸过大，导致有效内容的像素点仅有9个，致使误差比前种情况大。根据前面的分析，这其中有较大部分原因是由于对照图中分辨率的提升导致图案细节更加丰富，而在对比时使用了对比图中对应像素点的平均值，制作与参考图像素个数一致的对照图，因此背景噪声有所增加，在超过一定分辨率放大率的情况下，均方根误差应该有所升高而峰值信噪比应该下降，这是提高分辨率增加有效像素数量的一种体现。

表2 衍射距离d=10 m时，直接计算与分段衍射算法计算图像的erms和Rsn

5 结 论

S-FFT算法中，由于采样定理的约束，衍射距离将严重限制衍射面画幅尺寸，在较长衍射距离上有效数据分辨率很低。由于实际应用中采样率、波长、原始衍射面尺寸等因素均需要根据实验确定，因此直接计算无法解决上述问题。本文模拟计算结果表明，分段衍射算法可利用采样定理实现对衍射面画幅尺寸的灵活调整，从而使上述问题得以解决。如传输距离为1 m时，画幅大小为2 970.25 mm2，占比约为0.26%，有效像素只有676个。而利用分段衍射算法(以d1=d2=0.5 m为例)，画幅调整为25 mm2，占比提高到43.58%，有效像素为114 244个，数据量增加了169倍。造成误差的一个主要原因来自有效数据分辨率提高后，细节分布与低分辨率像素值之间的差别。在图像细节较丰富时，其差别较大。因此这种差别应视为优于直接计算的一种结果。波前采集进而对立体物体进行层析成像计算是课题组接下来研究的重点方向，而提高图像细节的有效数据分辨率，灵活控制衍射面画幅尺寸，对该工作的研究具有重要的基础作用。结果表明，分段衍射算法对于提高优秀算法的适用衍射距离，具有较高的推广价值。