铁路客运枢纽公交车调度研究

(重庆交通大学交通运输学院 重庆 400074)

一、引言

公交作为我国城市交通系统的重要组成部分，我国铁路客运枢纽站中的公交车调度问题基本上还停留在传统的人工调度层面，对铁路枢纽站中公交车的换乘调度并没有一个有效的优化模型。枢纽站内公交与其他主流交通方式之间不能得到有效的衔接，乘客换乘等待时间过长，枢纽站内部乘客滞留形成拥堵。

二、问题描述

我国铁路建设时间与经验的不足，枢纽内部的各种交通方式之间的转换衔接存在不匹配的情况，乘客不能及时的实现换乘，导致枢纽站内部乘客滞留，产生拥堵现象，各种交通方式之间不能很好的衔接，国内对于铁路客运枢纽中公交车的协调研究大部分集中于运能协调与换乘时间协调方面，以枢纽站系统成本最少为先提条件，乘客换乘总费用最少为目标建立模型求解出最优发车数与发车时间间隔。

三、调度模型的建立

铁路运行线路与时间基本是固定不变的，可变性很小，要想通过协调铁路的运行时间来实现公交的换乘极其困难；公交车的出发与到站时间受人为影响因素很大，运行时间的可变性较大，对公交车的运行进行调度来实现其他交通方式与公交车的衔接转换也较为容易。

考虑到公交公司的利益与乘客出行等待可接受性等方面，公交车的调度问题主要包含两个方面：发车数量，对于公交车公司来说，车辆数量的控制直接影响到成本的大小，要尽可能的使用最小的车辆达到最大的运载量，所以，对于公交公司来说控制公交车的发车数量尤为重要；发车间隔，乘客出行总是希望等待时间最小，最好是能够达到随到随走程度，处于前面说过的车辆控制的前提下，通过调整公交车的发车间隔时间来实现。

(一)运能协调

本文仅讨论站前广场的始发(终点)线路和途径线路停靠站两种情况。

(1)

N1始发站公交车线路数；P公交车辆额定载客人数；β换算成标准车换算系数；rm1始发线路公交车的理论极限满载率；ta1始发站公交车平均发车间隔

(2)

N2途经站公交车线路数；rm2途径站公交车理论极限满载率；ra途径站公交车理论平均满载率；ta2途径站公交车平均发车间隔

(3)

nb3——途径站公交车理论平均满载率

假设铁路枢纽的高峰小时到站客流换乘公交车的流量为Qmax，对比计算出的Q与换乘流量的大小：

若Q≥Qmax，表示现有的公交线路满足需求，不需要增加新的线路；

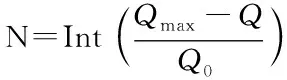
(4)

N新增加的公交线路数；Q0新增加的每辆公交车在高峰小时能够提供的接运能力

若计算得出的N≥1，则将结果取整得出需要增加的线路数；

若计算得出的N=0，则不需要增加新的线路，只需要通过调整现有的线路数来协调即可。

(二)时间协调

在铁路枢纽站中，换乘时间分为两部分：一部分为铁路枢纽站周边区域步行到公交车站候车的乘客的步行时间，另外一部分为从铁路枢纽站内部由其他交通方式(这里主要是铁路运输方式)换乘公交车的乘客的换乘时间。

1.枢纽站周围区域步行到公交站的总候车时间成本M2为：

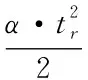
(5)

Qm1步行到公交车站的乘客流量；α乘客到达率；tr公交车发车间隔时间；φ乘客出行的时间价值

2.在一定的时间段[t1,t2]内，在铁路枢纽站内部由其他交通方式(主要为铁路)到达枢纽站并换乘公交车的总换乘时间成本M2为：

(6)

Qm2在一定时间内从第j次列车到达后换乘公交站的换乘流量；t0在一定时间内第1次公交车的发车时间；ti在一定时间内第i次公交车的发车时间(ti=t0+i·tr)；tj在一定时间内第j次列车的到达时间；tw乘客换乘公交车时从铁路站台到达公交站台的时间(包括出站检票和步行等时间)

此模型是以乘客的换乘时间总和最小为条件的函数模型，在乘客到达公交车站点客流特性不同的时间段[t1,t2]内，换乘时间成本的协调模型M=M1+M2，即目标函数为：

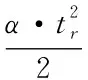
(7)

满足换乘时间成本总和M最小条件的情况下，求出最小发车间隔时间tr，其中，还需要满足以下约束条件：

t1≤ti≤t2(i=1,2,…n)t1≤tj≤t2(j=1,2,…m)

tmin≤tr≤tmax(tmin、tmax分别为根据正常情况下的铁路运输枢纽站客流研究出的能够满足相应的服务水平的公交车最小、大发车时间间隔，本文tmin=15min,tmax=30min)

四、结语

公交车是铁路枢纽运输系统的重要组成部分，对公交车的调度建立优化模型，可以根据计算出需要的公交车辆数和各时段最优的发车时间间隔，有效的节省公交车公司的成本，也能减少枢纽站中换乘公交车的等待时间，使客流由于等待车辆而滞留枢纽站的情况得到改善，有利于减少枢纽站拥堵情况，有利于完善城市交通系统，对居民的出行状况改善、城市拥堵的治理具有积极意义。