高中物理图像中“面积”的意义和应用

(江苏省启东中学，江苏 南通 226200)

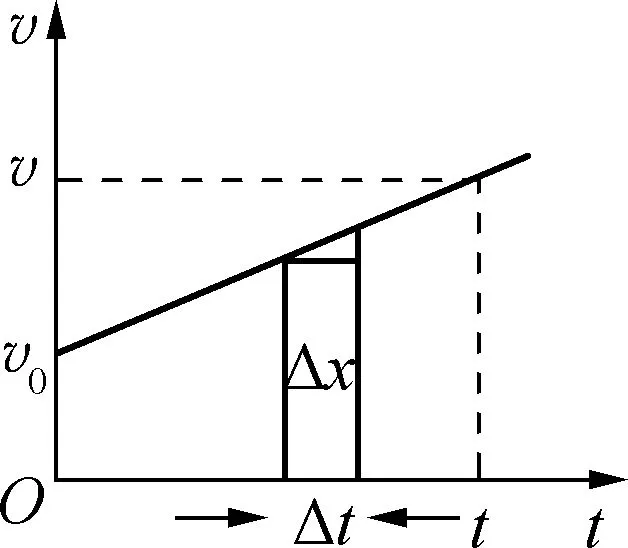
图1

高中物理中第一次接触到图像“面积”的意义,是在推导匀变速直线运动位移与时间关系时,教材中利用“微元法”说明v-t图像中图线与横轴包围的“面积”表示位移。图1为一匀变速直线运动的v-t图像,当把时间分割为无限个无限小的时间元Δt,每一个Δt时间内可以认为物体做匀速运动,则小矩形的“面积”可表示该段时间内物体的位移元Δx,然后对这些位移元求和,就可以用图线与坐标轴包围的梯形“面积”来表示t时间内物体的位移。这种利用微元法处理,看图线与横轴包围“面积”的方法,还适用于a-t、F-t、P-t、i-t、F-x、E-x、p-V图像，现将高中阶段常见的图形的“面积”的意义总结如下。

1 v-t图像中图线与横轴包围的“面积”表示位移

例1：某同学欲估算飞机着陆时的速度,他假设飞机在平直的跑道上做匀减速运动,飞机在跑道上滑行的距离为x,从着陆到停下来所用的时间为t。实际上,飞机的速度越大,所受的阻力也越大,则飞机着陆时的速度应是( )。

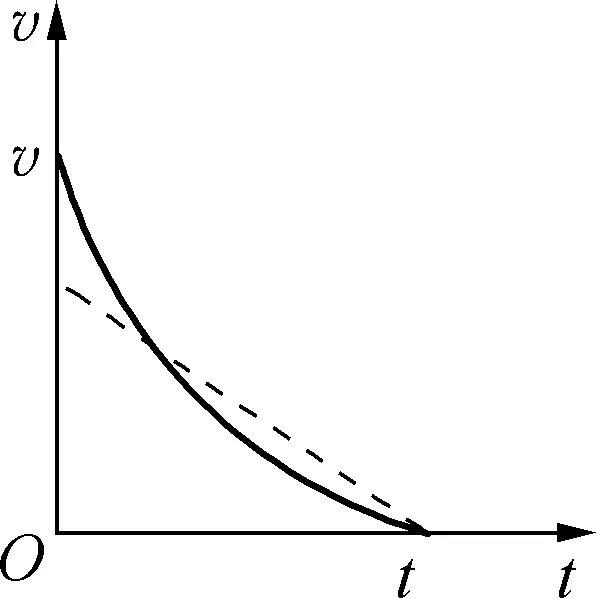
图2

2 a-t图像中图线与横轴包围的“面积”表示速度变化量

例2：一质量为2kg的物体受水平拉力F的作用,在粗糙水平面上做加速直线运动时的a-t图像如图3所示,t=0时其速度大小为2m/s,滑动摩擦力大小恒为2N,求0～6s内合力的功和6s时拉力的瞬时功率。

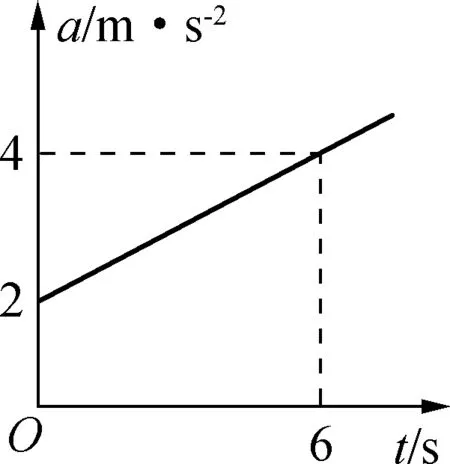
图3

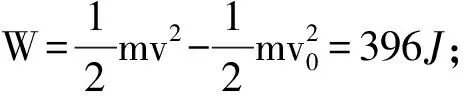
3 F-t图像中图线与横轴包围的“面积”表示冲量

例3：原来静止的物体受合外力作用时间为2t0,作用力随时间变化情况如图4所示,求0～2t0时间内合外力的功和合外力的冲量。

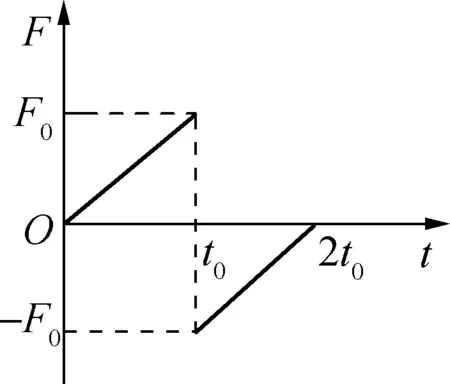
图4

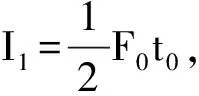
4 i-t图像中图线与横轴包围的“面积”表示电量

例4：如图5所示为一电流随时间的变化图像,求电流的平均值。

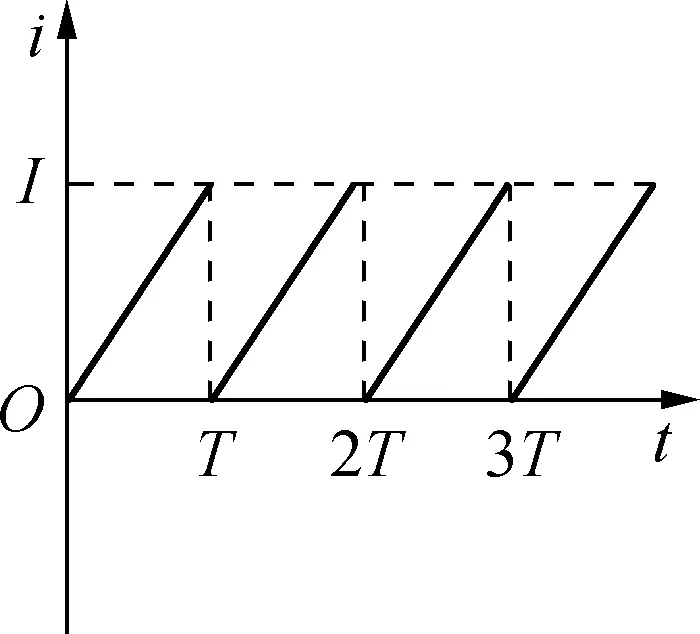
图5

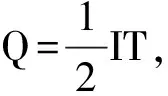
5 E-x图像中图线与横轴包围的“面积”表示电势差

令电场中两点沿电场线方向的距离为Δx,当Δx很小时,可认为两点间的电场为匀强电场,再根据公式U=Ed应用微元求和可分析得出E-x图像与x轴所围的“面积”代表电势差。

例5：空间有一沿x轴对称分布的电场,其电场强度E随x变化的图像如图6所示，试判断(x1，0)和(-x1，0)两点的电势高低以及(x1，0)和(x3，0)两点的电势高低。

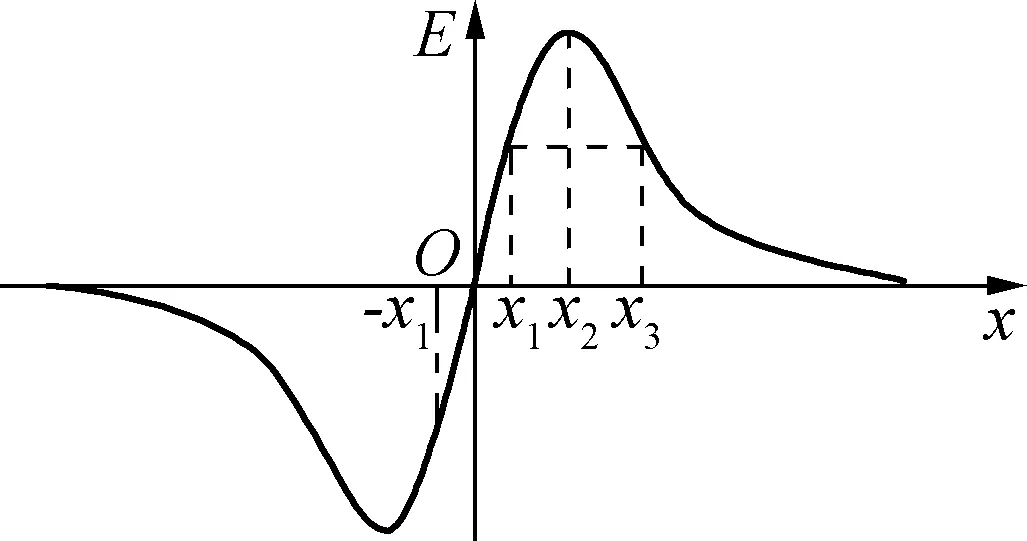
图6

解析：(x1，0)和(-x1，0)两点对应的E-x图线与横轴包围的“面积”相等,表示两点与O点的电势差相同,所以它们的电势相等。(x1，0)和(x3,0)两点的电场强度相等,由于与横轴包围的“面积”不相等,所以两点电势不等,由于沿着电场的方向电势降低，所以(x1，0)的电势高于(x3，0)的电势。

6 P-t图像中图线与横轴包围的“面积”表示功

例6：放在粗糙水平面上的物体受到水平拉力的作用,在0～6s内该拉力的功率与时间的图像如图7所示,求0～6s内拉力做的功。

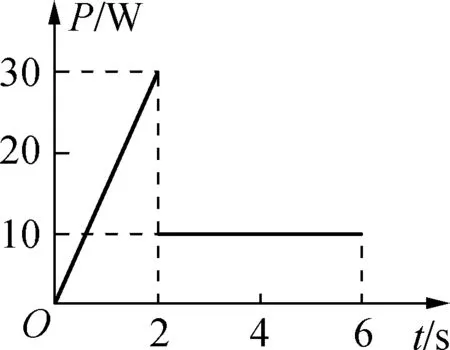
图7

解析：由W=Pt得P-t图像与横轴包围的“面积”表示功。所以0～2s内拉力做的功等于图像与横轴包围的三角形“面积”,2～6s内拉力做的功等于图像与横轴包围的矩形“面积”,所以0～6s内拉力做的功等于两个“面积”之和,即为70J。

7 F-x图像中图线与横轴包围的“面积”表示功

如作用力F为恒力,则F-x图像中,图线与横轴包围的矩形“面积”表示恒力所做的功。如作用力是变力,在高中阶段利用F-x图像定量计算的变力是随位移成线性变化的力。把位移进行无限等量分割,在极短位移Δx内可以认为作用力是恒定的,其所做的功可以用如图8的矩形面积表示,此面积称为该段位移内的元功ΔW,在发生位移为x的整个过程中,力F所做的功等于所有元功之和,即梯形的“面积”, 。

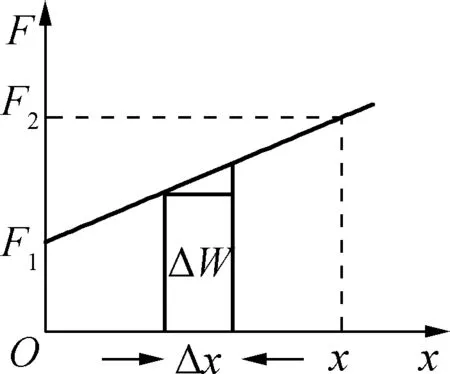
图8

例7：请利用弹簧弹力做功和功能关系，推导劲度系数为k的弹簧在其弹性限度内的弹性势能公式。

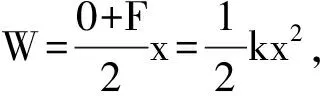
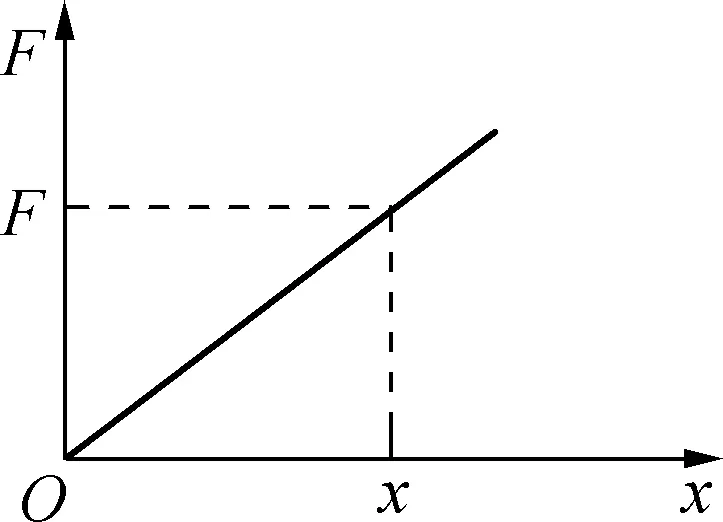
图9

8 p-V图像中图线与横轴包围的“面积”表示功

由W=FΔL，得W=pSΔL=pΔV,在p-V图像中图线与横轴包围的“面积”表示功。

例8：如图10所示,一定质量某一理想气体从状态A经ABCA循环回到状态A,试判断这一循环过程中气体从外界吸热还是放热?并求出吸收或放出多少热量?

图10

解析：气体A→B过程等容变化,气体对外不做功;B→C过程等压膨胀,气体对外做功的值等于BC图线与横轴所包围的矩形“面积”,即W1=pΔV=2×105J;C→A过程外界对气体所做的功等于CA图线与横轴所包围的梯形“面积”,即W2=4×105J。整个循环过程外界对气体所做的功等于循环过程的曲线所包围的三角形“面积”,即W=W2-W1=2×105J。由于整个循环过程气体温度不变,内能不变,根据热力学第一定律ΔU=W+Q，得Q=-2×105J,即气体向外界放出2×105J的热量。

在p-V图像中,按顺时针方向的循环过程中,循环曲线所包围的“面积”表示气体对外界做功的多少,按逆时针方向的循环过程中,循环曲线所包围的“面积”表示外界对气体做功的多少。

从以上例题及其解析可以知道,速度、加速度、力、功率、电流对时间元的累积分别是位移、速度变化量、冲量、功、电量,力、电场强度对位移元的累积分别是功、电势差,压强对体积元的累积是功。在物理图像中,这些累积的效应表示为图线和横轴所包围的“面积”,如果图线是线性的,则其面积在高中阶段利用初等数学可求;如果图线是非线性的,在高中阶段可进行定性分析,但定量计算需采用微积分处理。