基于图像处理的光弹应力测量实验

侯军渝 方子林 唐 芳

(北京航空航天大学 1仪器科学与光电工程学院， 2物理科学与核能工程学院，北京 100191)

光弹法是一种应用光学原理研究材料应力分布的测试方法。由于该测试方法直观性强、非接触、方便迅速，在工程校核中有着重要的应用[1]。光弹效应分析材料内部应力往往需要专业的软硬件，在物理实验中多是定性地观察光弹干涉图[2]。即使获取图像后通过手动描点计算，也只能简单获得少量点的粗略的应力分布情况。我们利用一般实验室均十分普及的软硬件，调整光路设置，采集高质量干涉图像，对等差线、等倾线采取相应的图像处理与数据提取，进行多点插值拟合计算。相较以往实验的定性观察或手动计算，该处理结果数据更丰富，精度更高，既能更准确地反映材料内部应力的变化趋势，也有助于加深学生对光弹原理的理解。除此之外，通过重复性验证以及与理论值的对比，对处理方法的可靠性有较为准确的评估。

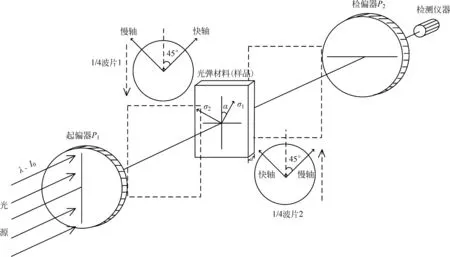
图1 正交平面(圆)偏振光场光路图

1 实验原理

1.1 光弹法测量应力分布原理

诸如环氧树脂等非晶体，在正常情况下具有各向同性的特点，不产生双折射现象，但当它们因受外力产生内应力时，就会变成各向异性而显示双折射性质，这就是光弹效应[3]。根据平面应力-光学定律其双折射率与外加应力成正比[4]，即

n1-n2=C(σ1-σ2)

(1)

式中，n1、n2分别为主应力σ1、σ2方向的折射率；C为光弹性系数[5]。

光弹实验中，入射光波长λ、光强为I0，将厚度为d的样品置于如图1所示的正交平面偏振光场中，经检偏器后光强度为

(2)

其中主应力方向与起偏器偏振化方向夹角为α，由样品材料双折射产生的相位差φ为

(3)

由式(2)和式(3)可知，干涉条纹的形状由主应力差相等的那些点的轨迹决定。样品上应力越集中的位置，主应力差的变化越大，因此干涉条纹越密集；反之亦然。根据干涉图样的这些特征，可以对物体的应力分布作定性和定量分析。

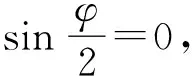
(4)

此时可以提取出等差线。

1.2 二维平面剪应力差法

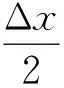
其中，σ1-σ2为各点最大主应力与最小主应力之差。

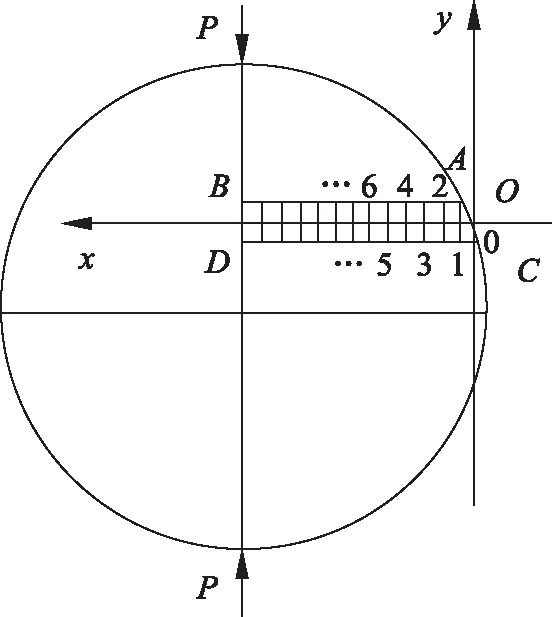
图2 坐标系建立和研究区域划分示意图

2 图像处理和计算

按照图1组装光路，考虑到成像质量与图像获取要求，光学系统前端以白板状态下的平板电脑作为平行白光光源。结合教学实用性，以手机和实验室常用的CCD作图像获取装置。本文所使用的手机型号为iPhone 6s，实验室CCD型号为PNT-628。其中，iPhone 6s采用的是1/3″ SONY CMOS，像素为1200万，单个像素尺寸1.22μm；实验室CCD采用的是1/3″ SONY CCD，像素约为44万，单个像素尺寸约6.3μm。故两者总感光面积一致，但iPhone 6s像素更高，能提供更小的空间分辨率和更多的像素点，而CCD的单个像素尺寸及其感光面积显然大得多，感光性能更好，信噪比更高。

2.1 测量材料条纹值

材料条纹值f0是光弹性力学中非常重要的一个概念，它是联系光学现象和材料应力的唯一参数[7]，亦是光弹性材料的主要性能参数之一。其物理含义是当样品为单位厚度时，光程差为单位波长时的主应力差值。因此，在进行应力计算前首先应测得材料条纹值f0。

由弹性力学知识和应力-光学定律可知

(11)

测得圆盘直径D后利用Tardy补偿法[8,9]，对圆片施加不同的压力P，通过旋转检偏器测量补偿角a，然后由初始级数N0进行运算求得中心条纹级数N1后，即可根据式(11)计算出条纹值。材料条纹值f0只与光源波长λ以及材料自身性质有关，与施加压力P无关[10]，故分别施力141.8N、245.2N、429.6N，计算后取平均值得到f0=8.474N/mm。

2.2 等差线获取与图像处理

考虑到后续处理过程中等差线图像提取灰度变化曲线的连续性要求，采用像素更高的手机获取图片。故在检偏器后用手机拍摄施力状态378.8N下的等差线图像。先通过Matlab对图片进行中孔径中值滤波等步骤降噪处理，其初步结果如图3(a)所示(坐标大小174*174，无量纲)。

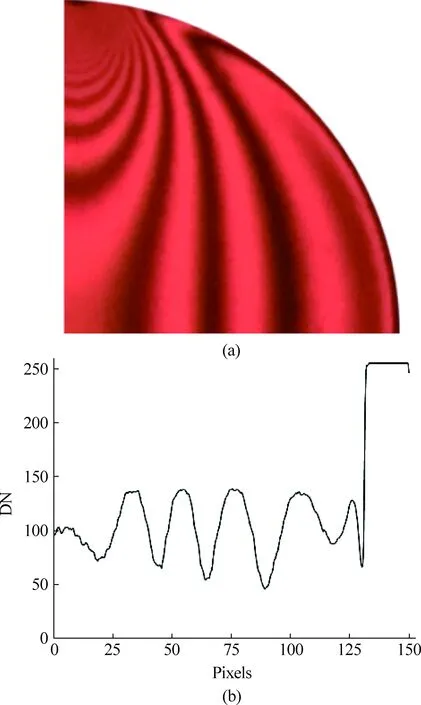
图 3(a) 施力378.8N等差线降噪图片； (b) AB线灰度提取曲线

分别选取距离上边缘90、95、100的3条线作为图2中的AB线、x轴、CD线，使用二维平面剪应力差法所述规则对3条线上的点进行编号，在Matlab默认坐标系(以图像左上角为原点，水平向右、竖直向下分别为x、y轴正方向，后同)下进行计算。以AB线处理为例，提取灰度变化图像。由图3(b)可知，经过滤波等步骤降噪处理后，灰度-坐标函数图像中波峰、波谷(对应明暗条纹中心)显著。

结合手动调整，选取各条纹级数边界点。根据所选点获得相应的坐标，对坐标点进行分段直线拟合。将拟合结果的两端向外延伸，代入相应点的坐标，计算其条纹级数N。x轴以及CD线的计算方法与此相同，其中x轴的结果如表1所示。

2.3 等倾线获取与图像处理

等倾线图像的边缘拟合对噪音的忍耐较低，因此采用感光性能更好、信噪比更高的实验室CCD获取图片，如图4。

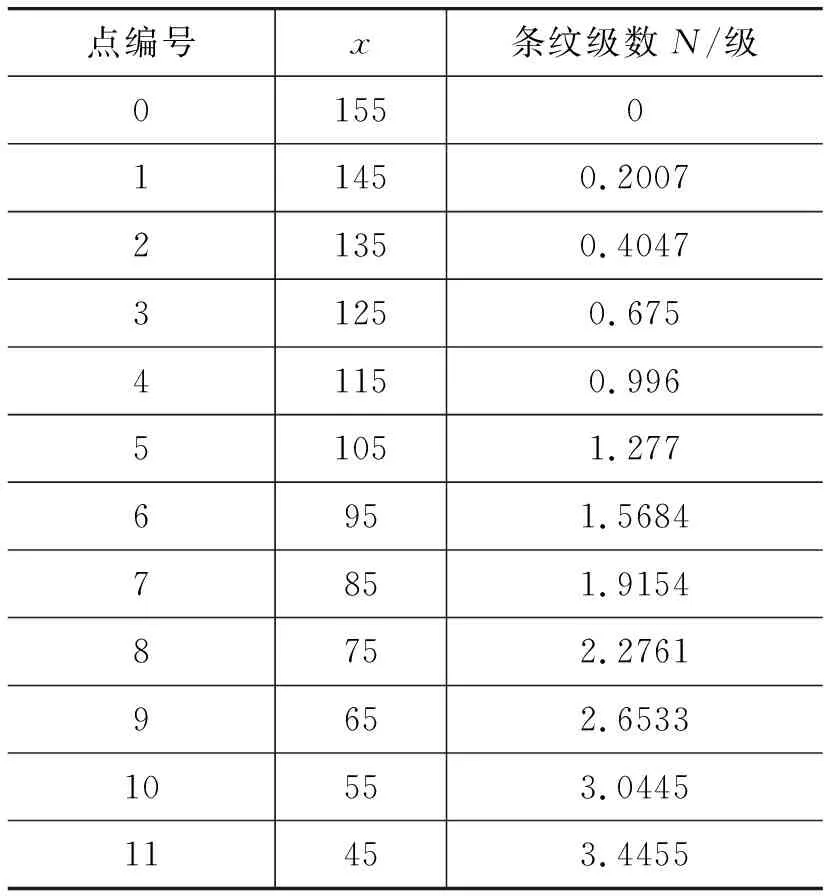
表1 x轴选点条纹级数

图4 施力378.8N时10°等倾线图片

为了得到高质量的等倾线，必须使等倾线区域更小、区分度更高，因此详细处理前先进行对比度调整和锐化处理，然后再利用Matlab进行Canny边缘检测，最后将检测点进行曲线拟合以得到等倾线。图片与等差线大小一致，最终结果如图5所示。

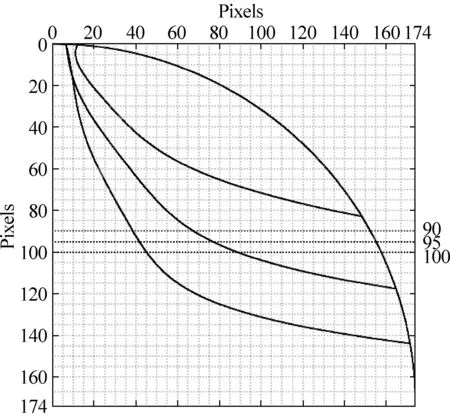
图5 10°至30°等倾线曲线拟合结果图

相同地，选取距离上边缘90、95、100的3条线(如图5)作AB线、x轴、CD线，进行插值拟合以得到非整等倾线度数。其中x轴的插值拟合结果如表2所示。

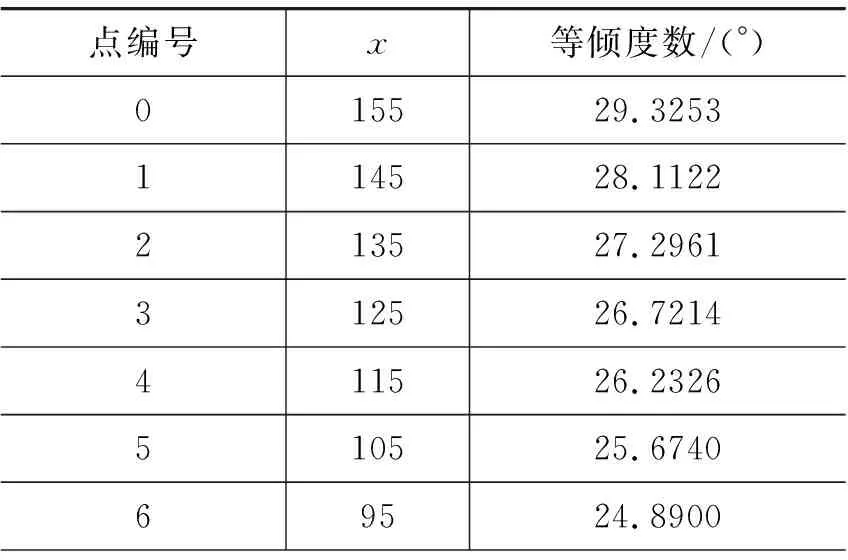
表2 x轴插值拟合等倾度数

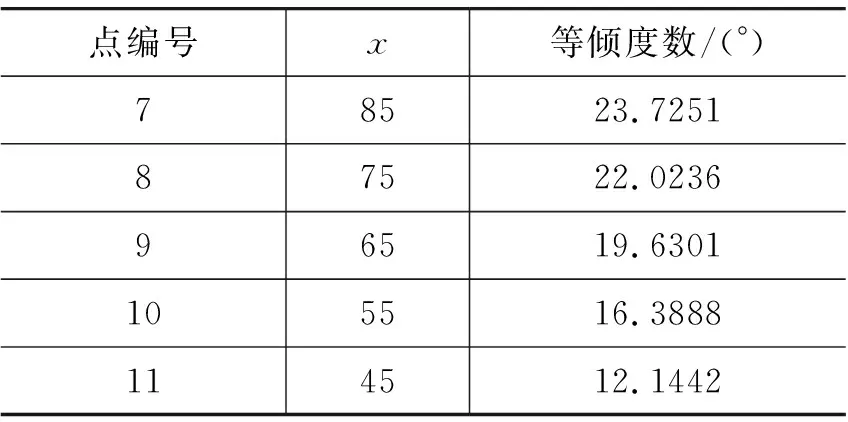
续表

3 实验讨论与对比分析

最后，根据图像处理结果，利用剪应力差法进行x和y方向上实际应力的计算，并将其结果与各向同性对径受压圆盘弹性力学解的理论值[11]进行对比。其中x方向上的正应力，光弹法测量值与理论值的对比分别如图6所示。由于y方向应力的变化趋势基本不变，实验值和理论值趋势又几乎一致，且存在的误差与x方向上的正应力误差密切相关(从剪应力差公式可知)，故本文仅展示x方向上正应力的对比图。

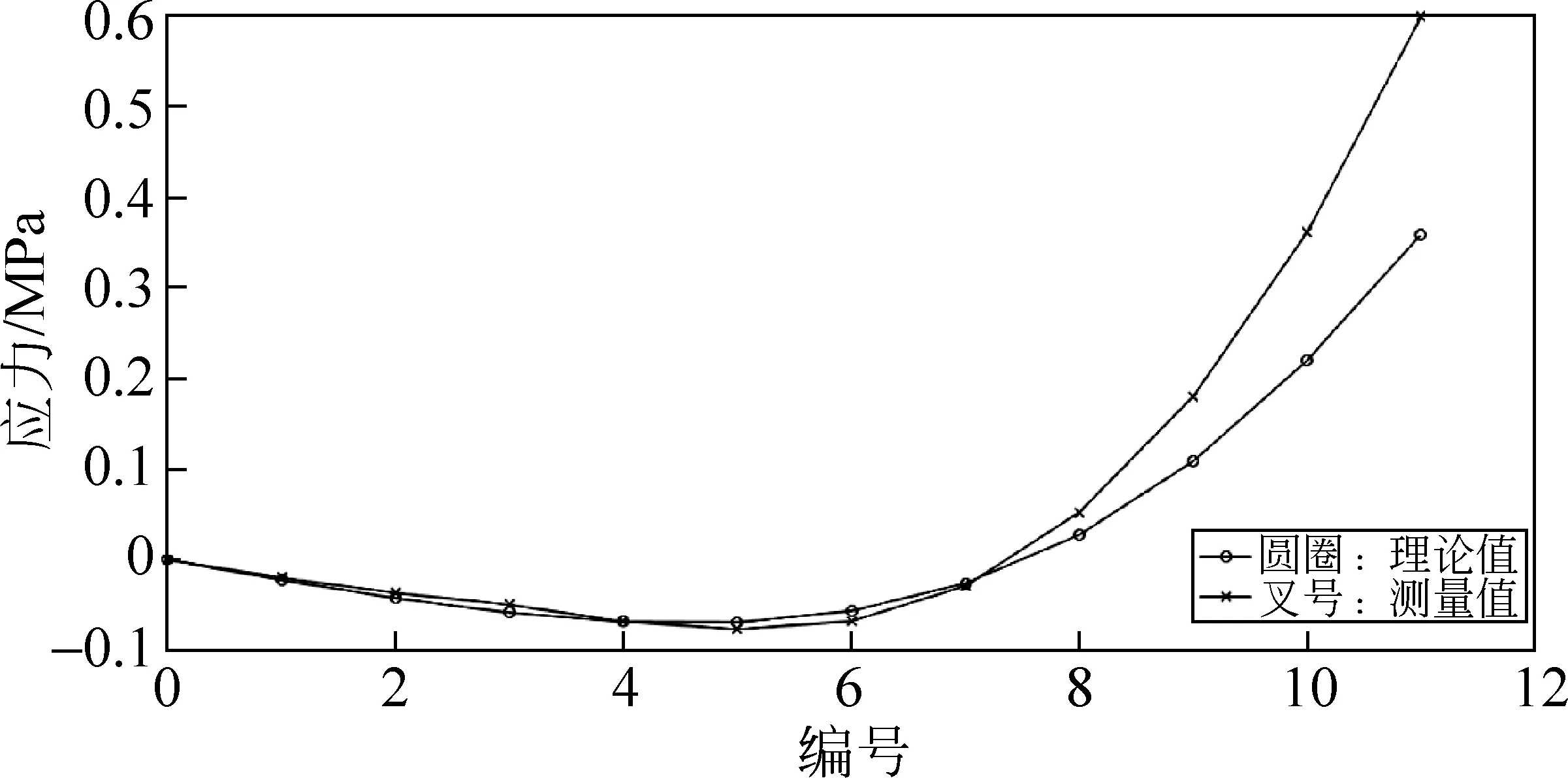
图6 378.8N力下x方向正应力对比曲线

对样品施加不同压力(分别为259.2N、180.4N)，按照相同的处理方法，得到材料内部应力的测量值与理论值对比曲线如图7所示。

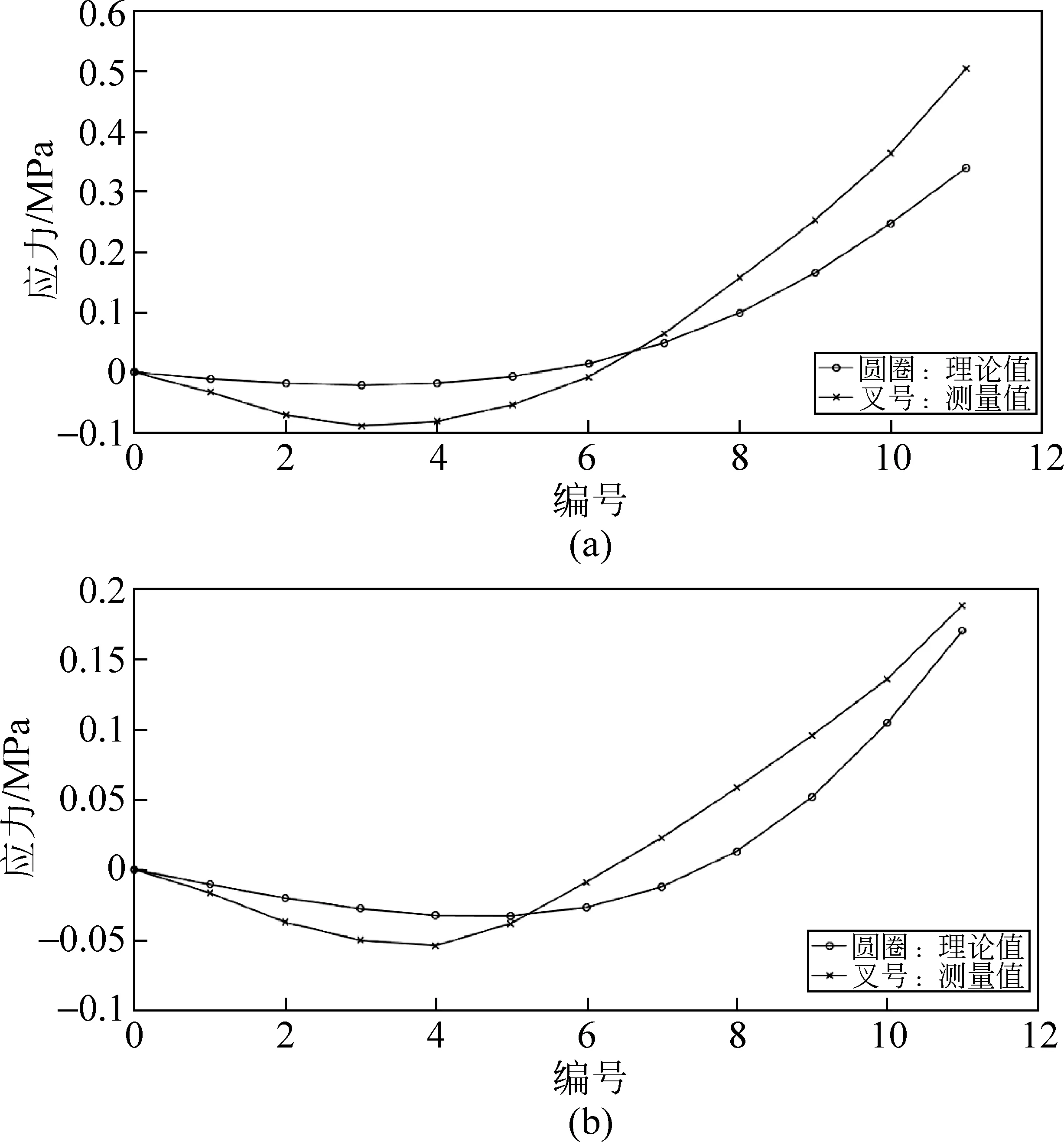
图 7(a) 259.2N力下x方向正应力对比曲线； (b) 180.4N力下x方向正应力对比曲线

由图6、7可知，对样品施加不同压力时对应的正应力理论曲线均呈先减小后增大的整体趋势，存在正应力的最小值和零点。施力378.8N时，x方向正应力的实验值和理论值符合度很高，仅在编号8点以后曲线上升速度略有差异；施力259.2N时，实验计算的正应力最小值与理论值间存在一定差异，零点和总体趋势仍旧保持了良好的一致性；而当施力180.4N时，实验计算的正应力最小值和零点较理论出现了一点偏差，但正应力变化趋势还是相符的。

虽然实验计算结果与理论计算结果存在着一定差异，但整体趋势一致，且误差具有规律性。因此，基于图像处理的光弹应力分布测量方法整体效果较好。且由观察可总结，x方向上正应力的零点位置，随着对径压力的增加越来越吻合。这说明本实验采用的方法对实际应力计算是可行的，有较高的准确度。并且施加的外力越大，条纹级数越多，利用灰度检测、拟合得到的非整条纹级数就越准确，正应力测量结果和理论值也就越接近。

根据插值拟合算法处理等倾线，角度误差最大值Δθmax≈0.05°。对于等差线，图片像素约为450px×450px。边缘点选取的像素误差ΔS最大值出现在条纹边缘处，根据处理原理有ΔS≤1px。以施加压力378.8N为例，考虑0.5级间最短距离l(l≈35px)和两端误差，条纹级数最大误差ΔNmax有

(12)

结合二维平面剪应力差法公式(5)～(10)，定量分析由于角度误差和边缘点选取误差引起单点新增误差。由计算过程中Δx=-Δy、Nmax≈3.446、θmax≈29°、θmin≈12°，单点新增误差的绝对值|Δ(Δτk)|有

(13)

即整个实验中，单点新增误差的绝对值均小于0.0272MPa。结合图6、7中理论曲线和公式(9)可知：在不同受力情况下，随着坐标点编号增大，Δτk先负后正，Δ(Δτk)和(σx)k也先负后正。由于单点新增误差的累积和抵消，实际误差((σx)k,测量-(σx)k,理论)先减小至最小值(负数)，后增大(由负变正)，故图6、7中理论值和测量值曲线先远离，后相交，再反相远离。

受器材和测量环境影响，本实验同样存在着系统误差。一方面，如本实验采用的圆片由于固定测力计导致边缘有细微缺口，这会影响干涉图样中等倾角度和条纹级数的分布，从而对正应力的计算产生误差。尤其施力较小时，各点应力理论值较小，在实际测量时更容易受到此类误差影响，由此造成的正应力最小值和零点的偏移也更显著。随着施力逐渐变大，各点应力理论值也逐渐变大，相对误差逐渐变小，累积误差和系统误差造成的曲线最小值点、零点的偏移也逐渐变小，理论值与实际值两曲线更加吻合。另一方面，在图像获取装置中，镜头透镜也会带来一定畸变误差。针对静态小视场，本实验尽可能利用图像中心部分，避免了畸变较大的情况。若有更高的精度要求，可使用标准棋盘图片，利用Open CV计算记录图片的畸变展开式常数，通过畸变展开式对图像畸变误差进行修正。

此外，实验中等倾线为每隔10°取一条，若减小间隔，利用Matlab的插值拟合会更加精确，误差也会减小。同时，由剪应力差公式可知x方向上的正应力误差越小，y方向上的绝对误差也越小。

4 结语

将光弹法与图像处理相结合，通过Matlab对手机采集的等差线图像进行滤波，借助PS对CCD记录的等倾线图像进行边缘锐化等算法处理。再使用Matlab完成图像的数据提取，进行插值拟合，进而完成多点应力分布的拟合计算。相较以往教学实验的定性观察或手动计算，计算机处理拥有更丰富的数据和更高的精度，处理后的多点拟合曲线也更能反映材料内部应力的变化趋势。通过和理论值的对比发现，施加对径压力越大，光弹法测量值与理论值的误差越小。并且本文提出的数据提取和图像处理方法涉及的软硬件均十分普及，便于一般实验室开展此教学实验。本实验方法同样也适用于教学实验中其他形状样品的内部应力分析。

■