社群化制造模式下基于反向传播神经网络的加工工时计算方法*

□ 程继辉 □ 金 阳 □ 贺靖伦

1.中车长春轨道客车股份有限公司信息化部 长春 130062

2.北京交通大学机械与电子控制工程学院 北京 100044

1 研究背景

工时定额是劳动定额的一种形式，指在一定的生产技术和生产组织条件下，企业基于充分利用生产工具，合理组织劳动，有效运用先进经验，为生产单位产品或完成单位工作而预先规定的劳动消耗量的标准，即生产单位产品或完成单位工作所需要消耗的时间。工时定额管理是企业的一项重要基础管理，是企业经营管理、经济核算的重要依据，也是企业计算产能和资源需求的重要依据［1］。传统的工时定额计算方法有经验估工法、秒表测时法、抽样调查法、预定动作时间标准法等，这些方法都需要对特定生产过程进行详细分析，进而计算获得这一生产过程的工时定额，不仅需要大量的人力和时间，而且人为因素较多［2］。

社群化制造模式是一种由专业化服务外包或众包驱动的，构建在社会化制造资源自组织配置与协作共享基础上的新型制造模式。通过社会化制造资源自组织，分散的社会化制造资源集聚形成各类分布式社群，并在利益协调及商务社交机制下，以社群作为运营主体进行分散的制造服务［3］。在社群化制造模式下，社会资源为了快速匹配制造任务，需要根据制造任务的相关特性，对制造任务加工工时进行快速计算，传统工时定额的计算方法显然无法满足社群化制造模式下工时计算的需求。

鉴于此，笔者提出一种基于反向传播神经网络（BPNN）的加工工时计算方法。这一方法通过构建一个三层的BPNN，将制造任务的相关特征作为输入量，将制造任务的工时定额作为输出量，建立相应模型。通过实际样本训练和仿真，确认这一方法提高了工时定额的准确性和效率。

2 BPNN概述

人工神经网络（ANN）是一种模仿大脑结构和功能的信息处理系统，由大量神经元和神经元之间的连接组成。ANN具有很强的自学习、自适应和自组织能力，并且具有很强的容错性。经过多年的发展，ANN已在许多学科和领域中得到应用和发展，其中包括工时预测和定额［4-6］。 熊伟［7］、郭凤国［8］等在分析影响零件工时的主要因素和工时定额特性的基础上，提出了基于有监督线性特征映射网络模型的工时定额计算思路，以便快速合理地估算航空发动机叶片数控加工工时。

在多种ANN中，BPNN是目前应用最广的神经网络之一，技术成熟［9-11］。BPNN是一种多层前馈网络，采用反向传播算法，网络的学习过程包括正向传递和误差反向传递两个过程，具有很强的非线性映射能力和泛化能力，能够很好解决工序工时预测问题。高忠华［12］通过MATLAB软件构建了某型发动机机体工时定额的BPNN模型。赵波［13］围绕船舶管制造的产品导向型作业分解，应用 BPNN研究了船舶管制造定额工时的标准化。笔者采用BPNN建立了社群化制造模式下制造任务特征和工时定额之间的非线性映射关系，从而准确、及时、有效地计算出加工工时。

三层BPNN又称单隐层神经网络，是BPNN中常用的一种网络结构。所谓单隐层，即只有一层隐层。三层BPNN结构如图1所示，三层分别指输入层、隐层和输出层［2］。

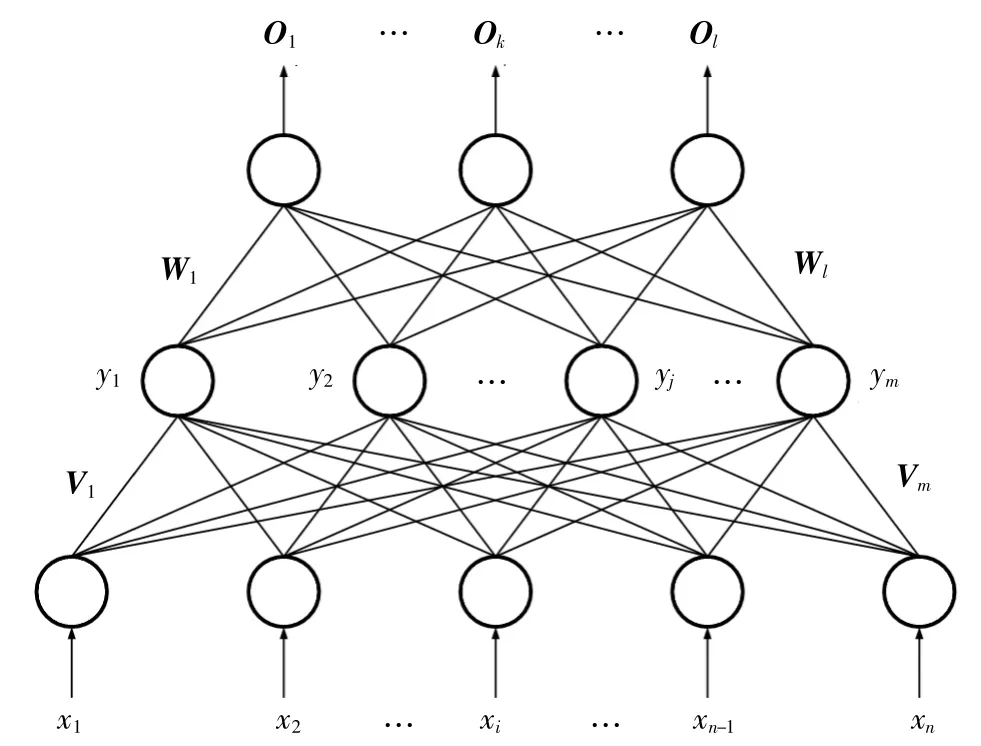
▲图1 三层BPNN

X=（x1，x2，...，xi，...，xn）T， 表示输入 向 量。Y=（y1，y2，...，yj，...，ym）T，表示隐层的输出向量。Y通过连接权值和传递函数的转换，得到实际输出向量O=（O1，O2，...，Ok，...，Ol）T。V=（V1，V2，...，Vj，...，Vm）T，表示输入层到隐层神经元之间的连接权值矩阵，其中Vj是矩阵中的一个列向量，表示输入层中所有神经元与隐层第j个神经元 之间相对应 的权值向量 。W=（W1，W2，...，Wk，...，Wl）T， 表示隐层到输出层神经元之间的连接权值矩阵，其中Wk是矩阵中的一个列向量，表示隐层中所有神经元与输出层第k个神经元之间相对应的权值向量。神经网络正向传递时，通过神经元之间的连接权值和各层传递函数的转换，将输入信息传递到各层。

对于输出层，数学关系式为：

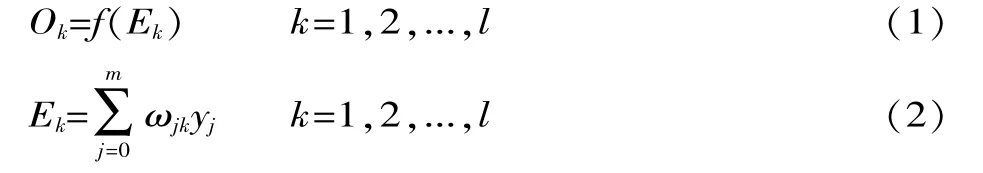
对于隐层，数学关系式为：

式（1）和式（3）中的传递函数f（x）需要根据实际的应用领域和数据进行选择。式（2）中的ωjk为向量Wk中与yj对应的权重，Ek为隐层各神经元对应Ok的加权和。同理，式（4）中的vij为向量Vj中与xi对应的权重，Ej为输入层各神经元对应yi的加权和。

在反向误差传递过程中，计算目标输出向量和实际输出向量之间的误差，并将误差通过连接权值和传递函数反向传递，同时调整权值矩阵。通过多次神经网络的学习和训练，使误差满足设定的标准，此时神经网络训练完毕。

3 基于BPNN的加工工时计算方法

基于反向传播算法，建立并训练神经网络，进而对某工序的加工工时进行计算。

（1）输入向量通过输入层和各层的传递，建立与输出层之间的关联，这样，样本的输入能够反映该工序与加工工时之间密切相关的特征。可见，样本特征的选择对于BPNN的训练效果有很大影响，所以根据具体工序的加工特征，选取与加工工时密切相关的特征形成输入样本，组成输入层数据。

（2）输入数据存在噪声、奇异样本等问题，需要对输入样本进行归一化处理，从而提高BPNN的收敛速度和准确度。通过归一化，将数据转换至［-1，1］之间。

（3）BPNN的训练过程受学习率、目标误差和最大训练次数等参数影响，因此需要对网络参数进行设置。

（4）建立神经网络结构，设置隐层节点数，选择每一层的传递函数。隐层节点数影响神经网络的收敛速度和结果的准确性，但目前没有公认的计算方法，笔者采用科尔莫洛夫映射神经网络存在定理来确定隐层节点数的大致范围［14］，并通过试错法调整并最终确定隐层节点数，以达到良好的训练效果。

科尔莫洛夫映射神经网络存在定理公式为：

式中：h为隐层节点数；m为输入层节点个数，即样本的维数。

（5）对神经网络的输出数据进行反归一化处理，得到最终的加工工时计算结果。

4 实例分析

笔者以某车间焊接工序为例，验证所述方法的有效性和可行性。根据焊接工序的加工特征，选取钢板厚度、焊条直径、焊缝厚度、焊缝长度共4个与工时相关的因素［7］作为输入特征，数据见表1。原始数据共29组，即共有29个样本。选择15组作为训练数据，用于训练所建立的神经网络，剩余14组作为测试数据，用于测试神经网络的有效性，通过MATLAB软件实现整个过程。

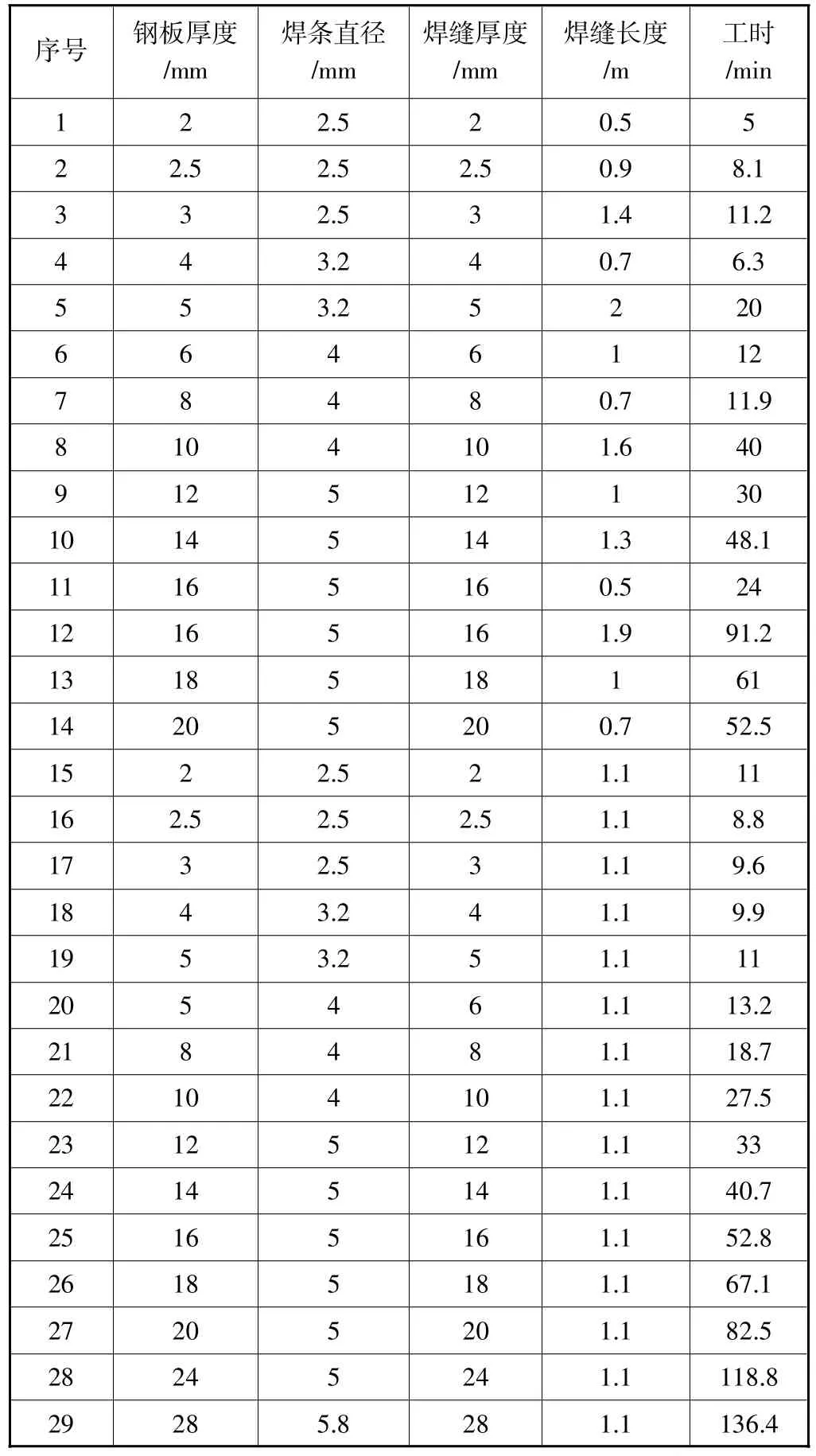
表1 焊接数据

利用MATLAB自带的Premnmx函数对各组数据进行归一化处理，转换至［-1，1］之间。由于归一化后数据存在负值，因此选取双极S形函数作为第一层传递函数，并采用线性函数作为第二层传递函数。隐层节点数上，通过科尔莫洛夫映射神经网络存在定理和公式确定范围，并不断调整，最终确定隐层的节点数为9。设定误差目标为10-6。将15组数据用于网络训练，并不断循环，直至达到设定的误差目标，训练过程如图2所示。由图2可知，当网络循环训练第570次时，达到了设定的误差目标，BPNN训练完成。

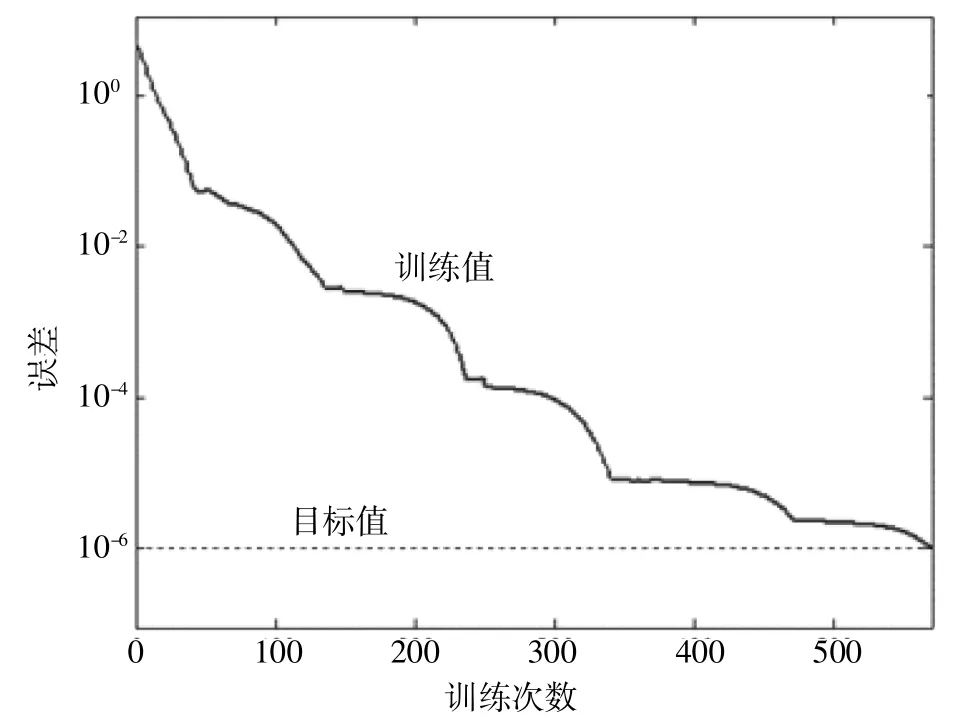
▲图2 BPNN训练过程

将14组测试样本输入网络中进行计算，计算结果见表2。可见计算结果与实际加工工时之间的平均误差在10%以内，计算效果良好。生成折线图，如图3所示，可以更直观地看出计算值与实际值之间的对比，验证了所述加工工时计算方法的有效性。

表2 工时计算结果对比 min

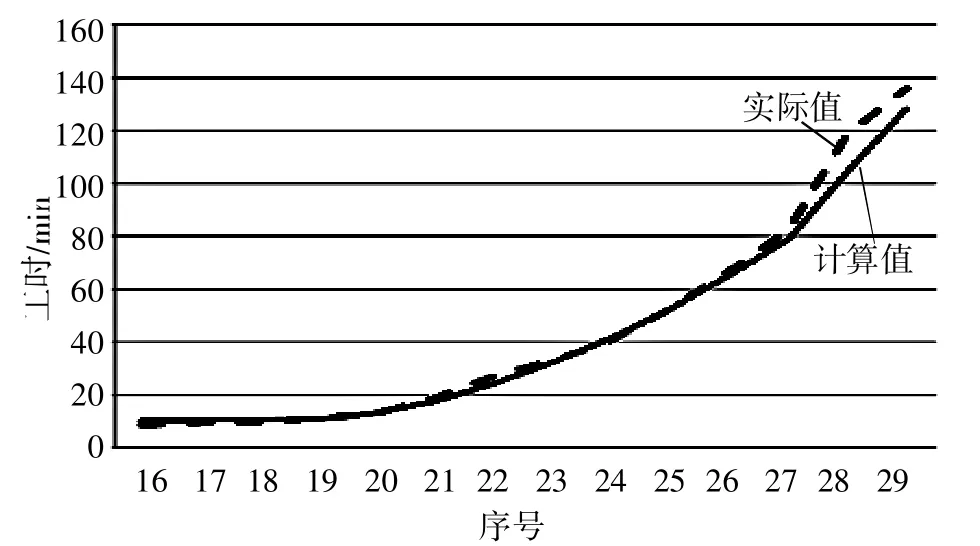
▲图3 工时计算结果对比图

5 结论

社群化制造模式是由分散的社会化制造资源集聚形成的各类分布式社群在利益协调及商务社交机制下的一种制造模式，是适应未来分布化、服务化和大规模个性化制造环境的一种新模式。在这一新模式下，社会化制造资源为了快速匹配社会生产任务，需要根据任务的相关特性快速、准确地计算制造任务的加工工时。笔者基于传统工时定额计算方法无法满足社群化制造模式需求的现实，提出了一种基于BPNN的加工工时计算方法，通过构建一个三层的BPNN，将制造任务的相关特征作为输入量，将制造任务的工时定额作为输出量，建立计算模型，并通过实际样本训练和仿真，验证了这一加工工时计算方法的准确性和可行性。