基于综合性能指标的喷涂机器人机构尺度优化

上海工程技术大学机械工程学院 上海 201620

1 研究背景

构型、性能和尺度是机构学研究的永恒主题。机器人机构设计的结果直接决定了机器人的工作空间大小、灵巧性、可操作度、各向同性、奇异位形、最大速度、最大加速度、传输精度等诸多运动学性能，而运动学性能又是机器人机构构型优劣评判的重要标准和尺度设计的前提条件。另一方面，机器人机构的多维尺度空间与性能指标间存在明显的非线性关系，很难用具有明确物理意义的无量纲参数来表达［1-2］。因此，采用精确量化的方法来描述和揭示机构尺度与运动学性能间的关系是机器人机构设计过程中具有挑战性的关键问题，对于机器人的研发及应用具有全局性影响。

美国的Gosselin等人将全域条件性指标定义为雅可比矩阵条件数的倒数在整个工作空间内的平均值，可用于评价整个工作空间中机器人输入、输出间传递关系的精确度及所有构形的相对误差均值，因而全域条件性指标被广泛用于机器人机构的尺寸设计［3-4］。但全域条件性能指标仅能反映整个工作空间内机构运动性能的平均水平高低，无法体现出机构运动性能的波动情况。在分析Gosselin等人提出的全域条件性能指标的基础上，石志新等［5］提出了全域性能波动指标。

笔者在考虑雅可比矩阵、黑塞矩阵在速度和加速度水平上对串联机器人运动性能影响的同时，突破了以往仅以雅可比矩阵为依据进行性能分析的局限性，并对经过尺度优化的串联喷涂机器人进行了运动学参数仿真，仿真结果证实了基于全域运动学性能指标的机构尺度优化方法的正确性。笔者所做研究为设计性能优良的机器人机构提供了理论依据。

2 串联机器人的运动学全域性能指标

2.1 全域条件性能指标

记雅可比矩阵为G，记黑塞矩阵为H，雅可比矩阵的条件数定义为kG=||G||||G+||，黑塞矩阵条件数定义为kH=||H||||H+||，G+、H+分别为G、H的广义逆矩阵。全域条件性能指标的数学含义是雅可比矩阵或黑塞矩阵条件数的倒数在整个工作空间内的平均值，表达式为：

式中：ηJ为全域条件性能指标；kJ为矩阵的条件数；ω为机器人的可达工作空间。

在计算||H||时，可以分别取H的每一层，这样||H||就有6个数，然后再计算kH：

根据矩阵范数的性质，可知 1≤kJ＜+∞，则ηJ取值范围为 0＜ηJ≤1，J∈｛G，H｝。ηJ值越大，就越接近 1，表明机器人在整个工作空间内的灵巧度及控制精度越高，运动学性能越好。

2.2 全域性能波动指标

机器人在实际使用中不仅要求机构具有良好的运动学性能，而且还希望保持良好的性能稳定性。针对全域性能指标的缺陷，笔者采用运动学全域性能波动指标：

式中：σJ为机器人全域性能波动指标。

机器人全域性能波动指标的数学含义为雅可比矩阵或黑塞矩阵条件数的倒数在整个工作空间内的均方差，其大小反映了机器人机构在整个工作空间内的运动性能相对于平均性能的波动幅度。σJ值越小，表明在工作空间内机器人的运动性能越稳定，机器人末端的输出运动也越平稳。

综合应用全域条件性能指标和全域性能波动指标，可以更加全面、精细地评价机器人全域运动学性能的好坏，从而更合理地优化机构的尺寸。当两个机器人机构的全域性能指标比较接近时，可以依据全域性能波动指标来进一步评判它们的优劣，进而选择性能较优的机构。

3 喷涂机器人运动学性能指标求解

3.1 喷涂机器人构型

笔者研究的具有六个转动关节的喷涂机器人构型及坐标系设置如图1所示，喷涂机器人D-H参数见表1。表1中扭转角αi-1为初始姿态下设定的角度，图1中β为偏交型手腕的偏角。

3.2 工作空间求解

结合运动学和Simulink软件中的SimMechanics模块建立系统模型，可以迅速准确地求解出喷涂机器人的工作空间［6-7］，如图2所示。求得的喷涂机器人工作空间由大量离散点构成。

3.3 雅可比矩阵和黑塞矩阵求解

雅可比矩阵和黑塞矩阵取决于机器人机构的位姿，并随机构位姿的改变而改变。根据影响系数法［8］，喷涂机器人雅可比矩阵的表达式为：

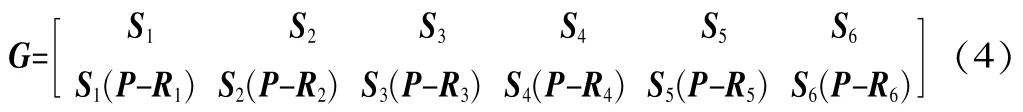
式中：Si（i=1，2，...，6）为串联机构各运动副轴线（Zi轴）在基坐标系O0-X0Y0Z0中的方向向量；Ri为各坐标系原点Oi在基坐标系中的位置向量；P为机器人手腕末端在基坐标系中的位置向量。

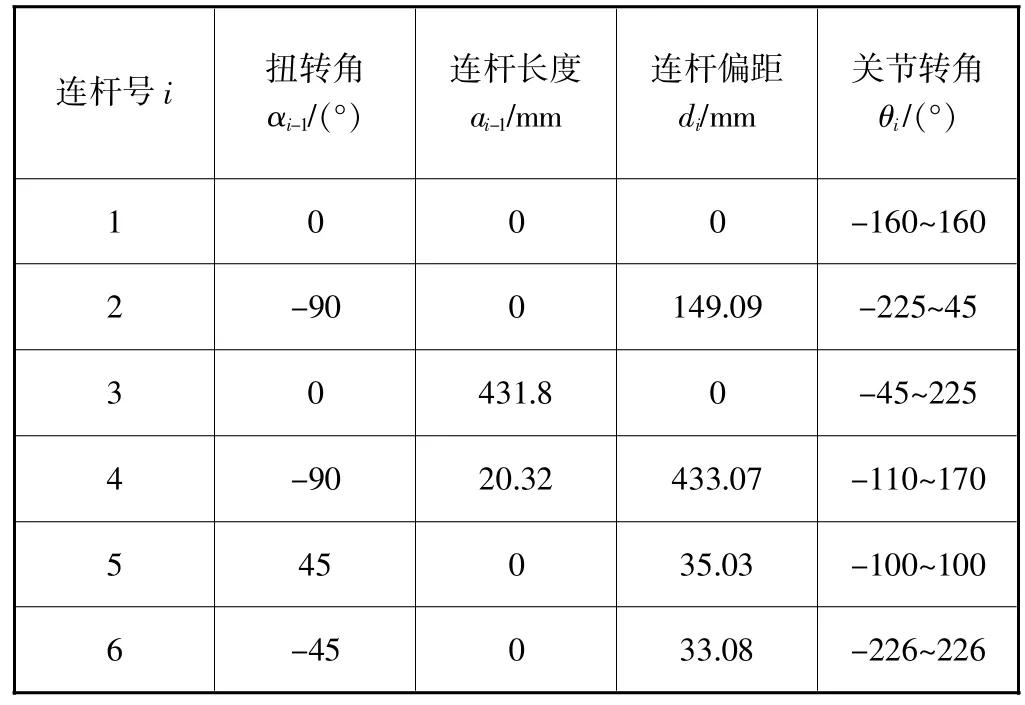
表1 喷涂机器人D-H参数

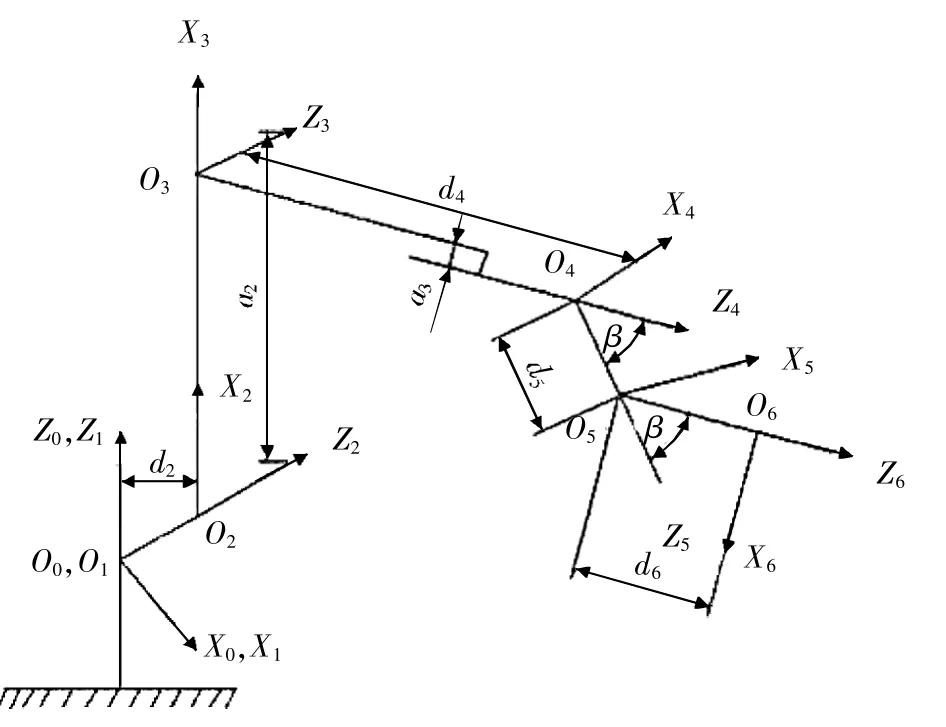
▲图1 喷涂机器人构型及坐标系设置

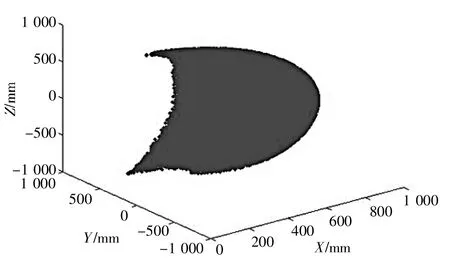
▲图2 喷涂机器人工作空间

串联机构各运动副对P的矢径为P-Ri，且Si、Ri、P均为3×1的列向量，由此可知雅可比矩阵G为6×6方阵。

喷涂机器人黑塞矩阵的表达式为：

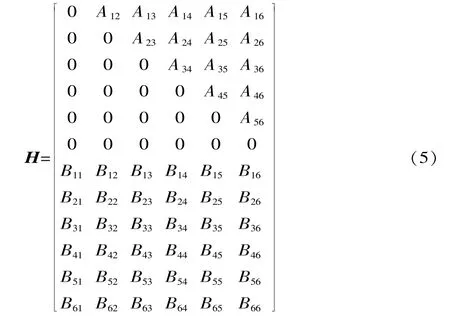
黑塞矩阵H为6×6×6的矩阵，其中的元素0均表示［0 0 0］T矩阵，采用Aij=SiSj、Bij=Si［Sj（P-Ri）］（i，j=1，2，...，6）向量积进行简写，Sj与Si的物理含义和本质相同，只是为了作区别，即Sj（j=1，2，...，6）同样分别对应串联机构各运动副轴线（Zi轴）在基坐标系中的方向向量。

4 机构尺度优化

笔者以图1中的a2和d4，即大臂及小臂的长度优化为例，按照上述方法得到了具有不同a2、d4尺度的机器人机构性能指标，求得了每组机构的运动学全域条件性能指标和全域性能波动指标数值，据此绘出全域条件性能指标图谱及全域性能波动指标图谱，如图3～图6所示。

由图3可知，当连杆参数a2=400～440 mm、d4=400～410 mm时，速度全域条件性能指标数值较大，表明喷涂机器人在此区域的速度全域条件性能指标较优。由图4可知，当连杆参数a2=400～450 mm、d4=400～410 mm时，加速度全域条件性能指标数值较大，表明喷涂机器人在此区域的加速度全域条件性能指标较好。综合图 3、图 4，当a2=400～440 mm、d4=400～410 mm时，喷涂机器人的速度及加速度全域条件性能指标均较为理想。由图5可知，当连杆参数a2=400～410 mm、d4=406～410 mm时，速度全域性能波动指标数值较小，表明喷涂机器人在此区域的速度全域性能波动指标较好。由图6可知，当连杆参数a2=403～413 mm、d4=409～410 mm时，加速度全域性能波动指标数值较小，表明喷涂机器人在此区域的加速度全域性能波动指标较好。综合图 5、图 6，当a2=403～410 mm、d4=409～410 mm时，喷涂机器人的速度及加速度全域性能波动指标均较为理想。

统筹考虑图3～图6，欲使喷涂机器人的速度、加速度全域条件性能指标及全域性能波动指标同时较优，大臂尺度a2、小臂尺度d4的取值范围应为a2=403～410 mm，d4=409～410 mm，此时可认为喷涂机器人的全域运动学性能最优。

5 运动学参数仿真

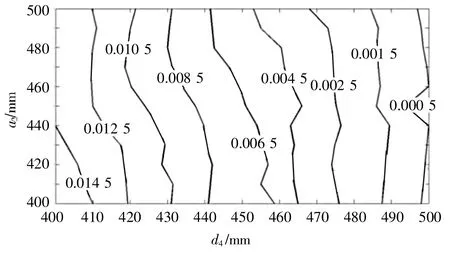
▲图3 速度全域条件性能指标图谱

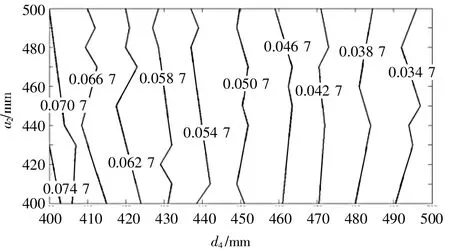
▲图4 加速度全域条件性能指标图谱

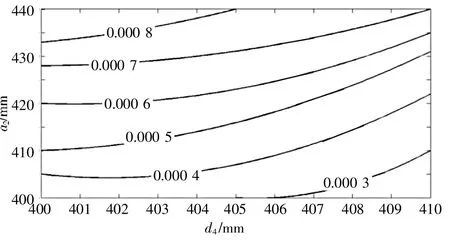
▲图5 速度全域性能波动指标图谱

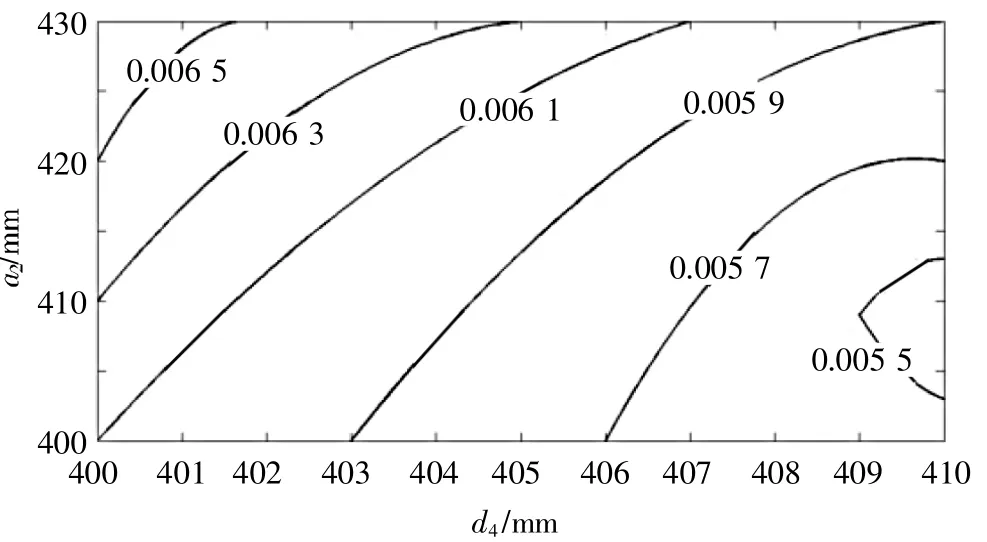
▲图6 加速度全域性能波动指标图谱

为验证笔者提出的全域运动学性能优化方法的有效性，需进一步考察具有最优a2、d4尺度的喷涂机器人运动学参数的变化规律。笔者在MATLAB软件机器人工具箱仿真环境中，令机器人以喷涂作业常用的矩形折线轨迹匀速喷涂阀门工件表面［9-12］。优化之后的尺度参数为a2=409 mm，d4=409 mm，进而研究机器人末端线速度、线加速度参数的变化情况。仿真得到的末端线速度、线加速度随时间变化的曲线分别如图7、图8所示。

由图7、图8可以看出，尺度优化后，机器人末端的线速度、线加速度曲线均呈现为更平滑、波动幅度减小，这表明尺度优化后喷涂机器人的运动更加平稳，控制精度相对提高，从而验证了笔者提出的机器人机构运动学全域性能优化方法的正确性。

▲图7 末端线速度随时间变化曲线

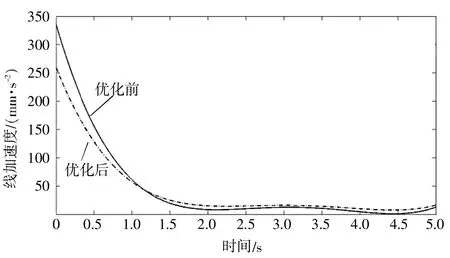
▲图8 末端线加速度随时间变化曲线

6 结论

笔者综合串联机器人运动学全域条件性能指标和全域性能波动指标，进行喷涂机器人的机构尺度参数优化。结合仿真证实了这一方法正确可行，且可操作性强、易于图形化，不仅能够全面评价机器人的运动学性能，而且能够精细、合理地优化机器人机构的尺度。