唯有研究活水来—— 一次对课本习题改编的意外收获

☉湖北省武汉市光谷实验中学 吴国庆

课本不仅是新课教学的蓝本，而且是复习备考的根本，我们教师在教学中抓纲务本，研究吃透教材，其必要性是不言而喻的.

面对中考复习备考，数学老师会为整天做不完的题目而烦恼，学生也会为负担重而抱怨，这时我们不妨把研究的目光转向课本，可能会从中得到意外的收获.下面就以笔者2018年中考复习备考中研究一例为线索，展示其过程，希望能够给读者带来启示.

一、研究过程

1.课本呈现

题1 （人教版九年级上册课本第101页习题24.2第6题）如图1，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠BAC=25°，求∠P的度数.

题2 （人教版九年级上册课本第122页复习题24第1题（3）小题）如图2，PA，PB分别与⊙O相切于A，B两点，∠P=70°，则∠C=（ ）.

A.70° B.55° C.110° D.140°

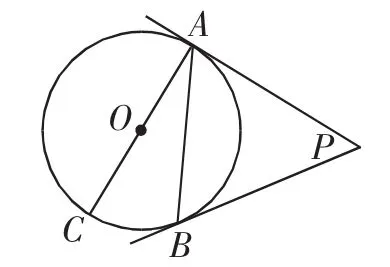
图1

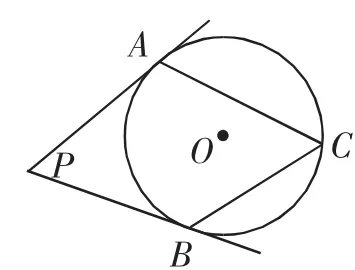
图2

两道题都涉及到切线长基本图，点C均在优弧AB上，只不过题1点C位置特殊，题2点C位置一般.从设问看，两道题都是涉及求角度问题，依据切线长基本图作基本辅助线，都很容易求出.

2.改编重组

由题1，2的相似点，两个问题比较容易组合起来，再赋予边的关系，融入三角函数，于是问题便会出现另外一片天地，如下题：

题3 PA、PB为⊙O的切线，A、B为切点，点D为优弧AB上的一点.

（1）如图3，证明：∠P+2∠D=180°；

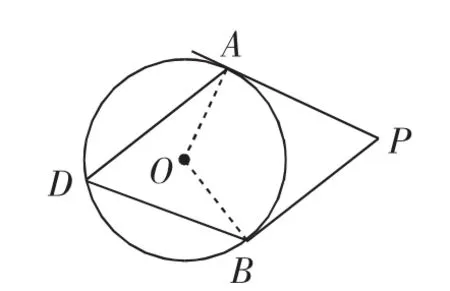
图3

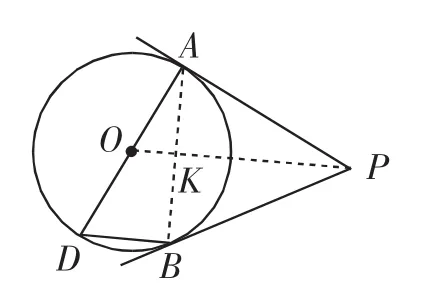
图4

解析：（1） 如图3，连接OA，OB，由∠AOB=2∠D，∠P+∠AOB=180°可证结论成立；

也可设OA=R，由AO2=OK·OP可得：OP=，由AO2+PA2=PO2可得：R2+90a2=，所以有（R2+9a2）（R2-10a2）=0，所以R2=10a2，AK=3a，所以tan∠D=tan∠AOK==3.

我们发现，解决问题的核心图形和辅助线并没有改变，从（1）问到（2）问中点D的位置，体现了一般到特殊关系.计算∠D的正切，其实只需转化到Rt△AOP中的射影图（即知OK，AP求射影图中其余线段问题），问题中设参不同，其计算量也会有差别的.通过图形改编重组演变，我们发现题目源于教材，高于课本，对学生的能力有一定要求.

3.再次优化

在备课组集体研讨下，结合本市中考命题方向，我们对试题又进行如下改编：

题4 如图5，PA为⊙O的切线，A为切点，点B为圆上一点，点D为优弧AB上的一点，∠P+2∠D=180°.

（1）如图5，证明：PB是⊙O的切线；

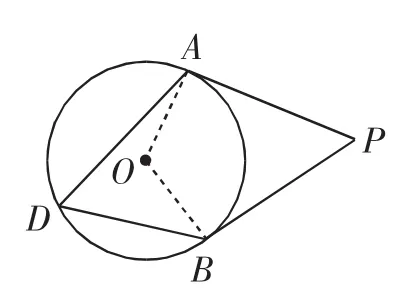
图5

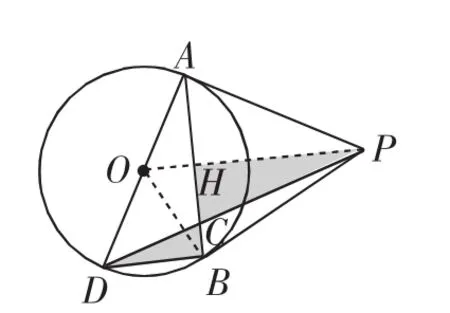
图6

解析：（1）证明：连接OA，OB，证OB⊥BP即可.

（2）连接OP，OB，OP和AB交于点H，由切线长基本图可得OP⊥AB，AH=BH，OP∥DB，△PHC∽△DBC，PH：BD=HC：BC，由BD=2得OH=1，由PB=3，设HP=x，由△OHA∽△AHP得AH：OH=PH：AH，所以AH=，由OH2+AH2=OP2-PA2得HP=9，故AH=BH=3，再设HC=m，由△PHC∽△DBC得9∶2=m（∶3-m），所以m=，AC=.

问题也可设OA=x或AH=x，得出的方程都是4次方程，一样可以求AC.

在题3基础上，对于（1）问，交换了问题的条件和结论；第（2）问将“BP∶BD=3∶2”改为“BP=3，BD=2”，让问题中线段长度以数值呈现，降低了设参计算难度，但问题变为求线段AC的长度，增加了图形中的相似难度，而且图形构造变得较复杂，增加了试题对学生能力的甄别性.

4.中考真题

题5 （2018年武汉市中考21题）如图7，PA是⊙O的切线，A是切点，AC是直径，AB是弦，连接PB、PC，PC交AB于点E，且PA=PB，

（1）求证：PB是⊙O的切线；

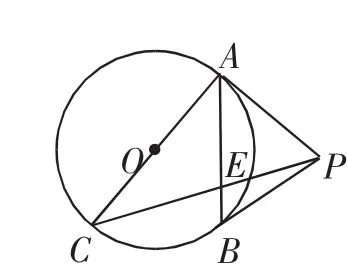
图7

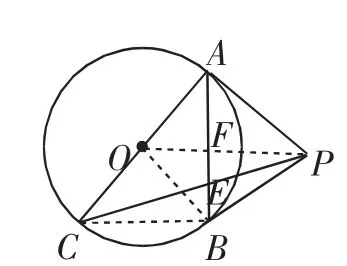
图8

解析：（1）证明：如图8，连接OB，OP，OP交AB于点F，通过△OAP≌△OBP可证明问题结论.

（2）如图8，连接BC，由∠APC=3∠BPC，可得∠OPC=∠BPC=∠BCP，所以CB=PB，设CB=PB=2a，则OF=a，设PF=x，仿照题3计算方法，可得

问题中（1）问还是回归到基本的三角形全等，有利于对几何中重要知识的考查，关注了基础薄弱的学生考试情绪，体现了人文关怀；（2）问中，命题者既关注了图形中角的关系，又着眼于线的关系，问题为求线段比值，而且稍微增加了计算难度，从而提升了试题综合度，更能全面考查学生的几何能力.

二、启示收获

数学课本是专家们按照课程标准编写，积淀了不少数学人的集体智慧，因此我们一线老师怎样读懂课本用好教材，这是一个长期的过程.在新课阶段，主要任务应该是从课本中教给学生新知，让学生掌握好数学基础知识，而在复习阶段，除了梳理知识成体系外，更多的应该是对课本进行深度挖掘，横向类比，增加知识的深度和广度.

各地中考试题，都体现出“回归课本”，如武汉市2018年中考，24道题中就有22道源于教材.中考复习，怎样做到减负增效，避免题海战术？从大量复习资料中走出，回归教材应该是出路，可怎样让“回归课本”落地生根呢？回归不应该只是知识简单重复，机械识记，应该是从思维高度上对课本进行深度思考融合，当然经过筛选后课本一些问题可以选作训练，可我们做的大量工作应该是对问题进行重组、深化、演变、拓展，生成新的复习题，让初中数学核心知识和方法融入复习题，通过复习题训练学生方法和思维，从而提升学生在中考中的竞争力.

文中笔者在中考前对课本习题重组改编深化，并不是有意“猜题押题”，但出现解题主体思想和中考题高度相似的情况，纯属巧合，但我们毕业年级数学老师应该初心不变，即“中考复习，抓纲务本，减负增效，以人为本”.