关注学生多维体验，提升数学学习效率

☉江苏省南通市虹桥二中 周栋梁

教学中体现数学问题的本质并对知识形成过程进行揭示一直是现代数学教学特别强调的目标.教师应引导学生进行不同形式的自主学习与探究活动并使其能够对数学发现与创造的历程进行体验，倡导学生在自主学习、研究性学习中锻炼自身的创新意识.学生亲身经历这一独特的体验是教师教学中应该重点关注与引导的.学生在亲身经历知识发生、发展、形成过程中所获得的求知的快乐往往能够真正激发他们学习的内在动力并因此提升课堂学习的效率.因此，教师在实际教学中应始终不忘促进学生探究的问题与活动的设计，使学生能够在开放、互动、新型的教学环境中形成探究结论、发现问题的感悟.

一、在阅读中体验

很多教师的教学习惯因为新课程的实施与推进得以大大转变，不过课堂教学迎来诸多新气象的同时却也不能完全排除一些传统教学的行为，不重视教材、满堂灌的教学现象仍有存在.很多教师在阅读上的疏于指导，从而使学生无法对教材产生体验，概念不清、公式不明、生搬硬套、解题不规范等不良现象在学生的数学学习中比比皆是.学生在有效的阅读中往往能够更加真切地感受知识的延续与方法的美妙，不仅如此，学生还能在阅读中提升感悟能力并对作品中的数学思想展开探索.

文字语言、数学符号语言、图形图标语言的转换在数学学习中是一项重要的内容，学习者如果能对研究对象进行自如的语言转化也就意味着他对知识的理解越发透彻.

案例1 在研究二次函数y=a（x+m）2+n（a≠0）的图像与性质时，教师可以引导学生对材料进行阅读并解答以下问题.

问题1：分别说出函数y=ax2（a≠0）、y=ax2+n（a≠0）、y=a（x+m）2（a≠0）的图像与性质.

问题2：请对上述函数图像与性质之间的联系进行描述.

问题3：二次函数y=a（x+m）2+n（a≠0）的图像与性质可以确定吗？

教师引导学生在教材的阅读中对二次函数的图像与性质进行更深入的认识，使学生能够在阅读与认识过程中对“从一般到特殊”“数形结合”等一般性数学研究方法进行感悟与体验，对凝练的概念用词形成理解，使学生在阅读与对比中对二次函数y=ax2（a≠0）、y=ax2+n（a≠0）、y=a（x+m）2+n（a≠0）的图像与性质进行区别和联系，学生在阅读、比较与联系中往往能够对概念与实例形成更加深刻的理解.

二、在探究中体验

教师如果将数学教学视作简单“告诉”那就大错特错了，事实上，数学学习应该是学生个性化的思维体验.学生在数学学习中所获得的体验是否深刻与丰富往往与问题情境的创设有很大的关系.因此，教师应尽量创设出针对性强且适合学生的体验情境以诱发学生的认知冲突，使学生在活跃的思维活动中不断丰富想象并对知识进行再发现与再创造，这对于学生能透彻理解知识来说是至关重要的.

案例2 运用从特殊到一般的方法研究“三角形内角和定理”.

第一步，从三角板与正三角形的三个角上引导学生发现其共同具备的属性：90°+60°+30°=180°，90°+45°×2=180°，60°×3=180°.

第二步，提问：“是不是任意三角形的三个角都存在这样的关系呢？”请学生画出一个任意三角形并用量角器进行各个角的测量，将测量所得数据记录在表1之中，学生很快发现测量所得的数据之和与180°相等或比较接近，教师适时追问：“为什么有的数据之和是接近180°的呢？”（有误差）定理的结论顺利得出.

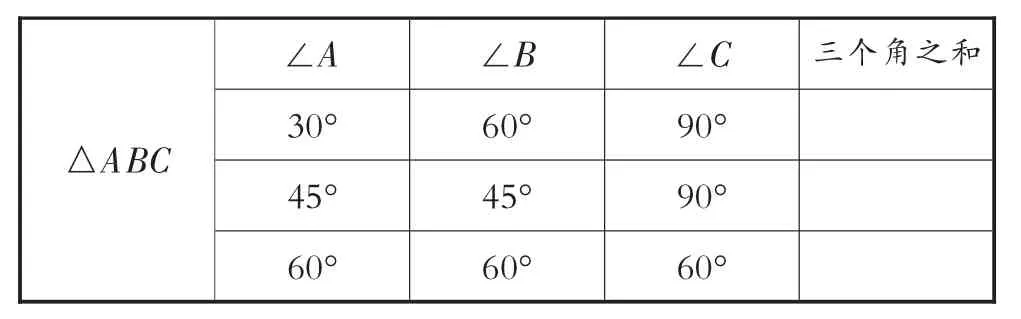
表1：

第三步：设计一系列问题并引导学生进行联想与证明.

师：已经学过的知识当中有跟180°相关的吗？

生1：平角、邻补角以及平行线的一组同旁内角等知识是与之相关的.

师：三角形的三个角之和等于平角这一结论应该怎样证明呢？

生2：一个角保持不动并将另外两个角移过来接上就可以了.

师：同旁内角互补又应该如何制造呢？

生3：作平行线.

学生一边思考一边画图进行了证明方法的多种尝试（如图1）.

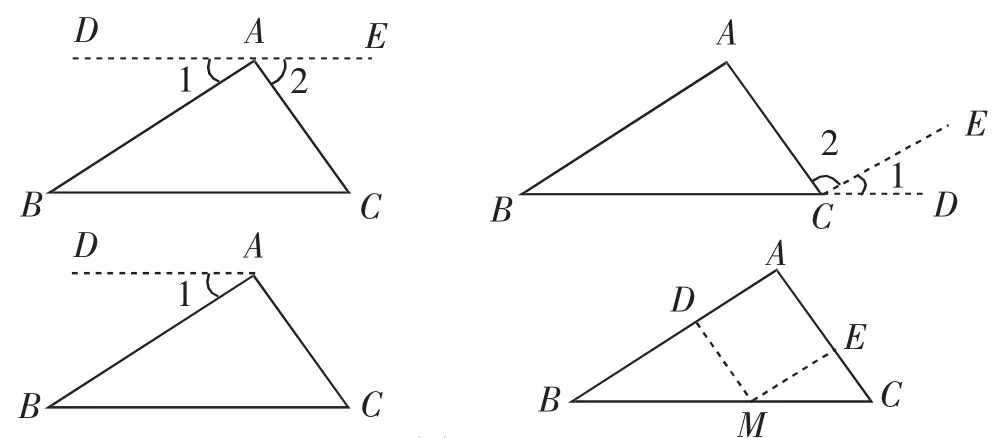
图1

三、在实践中体验

学生的很多体验必须建立在动手实践的基础之上，课内知识在实践中得以深化的同时还能锻炼学生的实践能力，不仅如此，学生在实践中获得的数学体验是远非观看幻灯片所能比拟的.

案例3 反比例函数的图像与性质.

这一内容的传统教学存在双曲线的形成、双曲线与两坐标轴无限逼近的理解这两大难点，“教师示范—学生模仿练习”是一般传统教学的模式.教师可以引导学生在画图软件的操作中对自变量进行赋值变化并作出双曲线，然后发现反比例函数的图像与性质，学生对在这种实践操作中得来的体验与感悟印象极为深刻.

四、在思维碰撞中体验

学生在独立思考的基础上进行探索、实践、交流才能对数学对象形成更为全面的理解与体验，对很多易错点与探究点的认知也会因此更为深刻.

案例4 复习课上的一道方程练习：已知关于x的方程（3k+1）x2-2x-1=0有两个不相等的实数根，则k的取值范围如何？

生1：因为两实根不相等，因此b2-4ac＞0，

教师听后一笑：有补充的吗？

生2在提醒后补充：这一方程是一元二次方程，因此必须保证二次项系数3k+1≠0，即k≠-，则k的取值范围为k＞-，且k≠-.生3举手：生2说得有道理，不过结果不对，因为k≠-不在k＞-的范围之内，所以k的取值范围应该还是k＞-.

师：还有其他陷阱吗？

学生纷纷表达自己的想法，有学生突然说：被开方数k应该大于0才对.

师：很好，你来说说看.

五、在深化中体验

一些学生在新情境变化之后往往会在解决问题时感觉困难重重，这主要是因为学生对数学学习的动态发展无法建立有效的信息关联所致.学生对题中信息无法提炼、对已有知识与题目信息之间的关联无法构建是导致这一现象产生的最根本原因.因此，教师在教学中应关注并培养学生创新意识的发展，适当运用题组教学、变式教学改变学生相对封闭、固定的思路，使学生在更高层面上对数学对象的本质进行理解并获得技能的巩固、思维的拓展和迁移.

案例5 概率问题的题组练习：

（1）连掷两枚骰子时点数相同的概率为多少？

（2）将图2中的转盘连续转动两次，则转两次得到的相同颜色的概率如何？

（3）将6个小球分别编上1-6的数字并放于一不透明纸箱中，在纸箱中先摸出一个球，放回后再摸一次，连续两次摸球所得的数字相同的概率如何？

（4）运用计算器连续两次产生1～6的随机整数，两次所得的随机整数相同的概率如何？

题组教学、变式教学往往能使学生在探究中体验到无法预料的东西，对上述四个小题进行审视，我们不难发现其中所蕴含的数学模型都是相同的，在一个基本问题上逐层深入并进行类比、联想、特殊化以及适度拓展所获得的一组练习使得问题的本质更加透彻地展现在学生面前，学生在多题一解的题组练习中对同一数学模型与数学思想方法展开探索，由此获得的体验以及思维的深刻性都是普通练习无法相提并论的.H

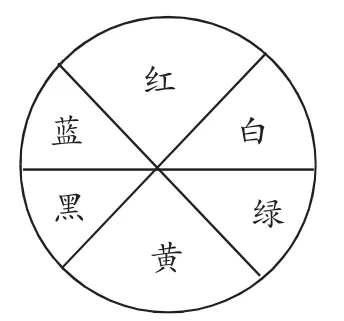
图2