主跨40 m跨座式单轨交通连续钢箱轨道梁优化设计
董艳彪,刘世忠,王冠军,魏 源
(1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州 730070;2.林同棪国际工程咨询(中国)有限公司,重庆 401120)
跨座式单轨交通是一种车辆直接骑跨在单根轨道梁上运行的特殊轨道交通方式[1],轨道梁既是轻轨列车的导轨,又作为承重梁发挥一般梁桥的承载作用[2]。作为列车导轨,其截面宽度等于列车轮间距,故截面宽度较小,横向刚度小,横向稳定性较差。对于钢箱梁,一般采用双线设计,两片单梁之间通过钢横联连接成为整体,提高了横向刚度与稳定性,同时增加了其美观性。我国跨座式单轨交通工程正处于起步阶段,列车轨道梁主要采用预应力混凝土PC简支梁,钢轨道梁应用较少,所以对钢轨道梁的研究也相对较少。鲜有研究连续钢箱轨道梁梁高、边跨与中跨比优化设计方面的文献。
为满足大跨度跨座式单轨交通轨道桥梁建设的需要,连续钢箱轨道梁因其自重小、跨越能力强、施工速度快等优势逐渐倍受工程界青睐。而连续钢箱轨道梁的梁高、边跨与中跨比对结构的受力特性影响显著,所以合理选取梁高、边跨与中跨比成为连续钢箱轨道梁设计中较为突出的问题。本文以某市云轨示范线一主跨40 m等截面连续钢箱轨道梁为工程背景,对不同梁高、边跨与中跨比的结构体系进行力学特性计算分析,探讨梁高、边跨与中跨比对该桥主梁挠度、竖向基频、梁端转角、应力等方面的影响。通过对计算结果进行比较,选出在结构各项力学指标均满足规范要求的前提下,使得结构材料用量较少,受力最为合理,能够最大限度地发挥材料作用的最优梁高、边跨与中跨比。
1 结构优化原理
1.1 结构优化方法
桥梁结构常用的优化方法有很多种,如:直接搜索法、应力比法、齿形法、最小应变能法、复形法、惩罚函数法、单纯形法等[3]。由于本文仅考虑2个参数的优化,所选变量较少,所以选用直接网格搜索法原理、采用双变量优化设计方法进行优化。基本思路是:先估计设计变量变化范围;在此范围内划分网格(等分或不等分均可)形成网点;然后求各网点的目标函数值和约束函数值,将各网点的目标函数值与约束函数值进行对比,在满足约束条件下的各网点中选出最优解。如果需要进一步提高精度,可以在目标函数最优解附近加密网格,再进行继续优化。具体步骤为[4]:
3)在各网点逐一检验是否在可行域内,然后对可行点计算其目标函数值,比较大小选择最小的X(s)。
4)取X∗=X(s)。如需在X(s)附近加密网点,取
1.2 目标函数及约束方程
对于本跨座式单轨交通连续钢箱轨道梁,优化的最终目标是使结构在竖向挠度、梁端转角、竖向基频满足规范要求,同时结构受力符合或接近等强度设计原则的前提下,最大限度地减少材料用量,使得设计更加经济。
1.2.1 目标函数
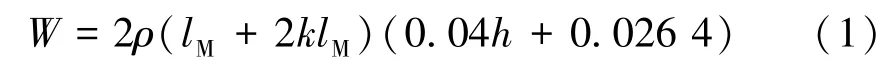
式中:W为结构自重;ρ为结构重度;lM为中跨长度,取40 m;h为梁高,k为边跨与中跨比,两者均为设计变量。
1.2.2 约束方程
1)应力约束下的约束方程为
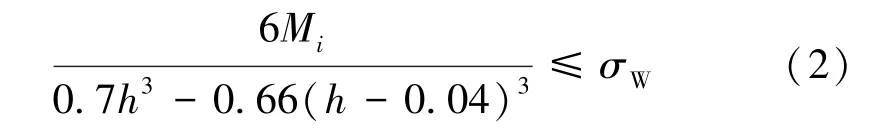
式中:Mi为控制截面弯矩;σW为容许应力。
2)竖向挠度约束下的约束方程为

3)竖向基频约束下的约束方程为

式中:f1为结构竖向基频;f∗为结构竖向自振频率限值。
4)梁端转角约束下的约束方程为[5]

式中:θj为第j跨最大梁端转角;θ∗为梁端转角限值。
2 梁高、边跨与中跨比优化范围的确定
为分析连续钢箱轨道梁边跨与中跨比的取值范围,参照文献[6],对10座我国目前已建的轻轨、铁路和公路连续梁桥边跨与中跨比进行统计,以此作为参考。统计结果见表1。

表1 国内部分连续梁桥的边跨与中跨比
由表1可知,10座我国已建连续梁桥的边跨与中跨比最小取值为0.600,最大取值为0.941,主要分布在0.6~0.9,故选取边跨与中跨比为 0.6,0.7,0.8,0.9进行优化分析。
文献[7]中指出:中国连续钢箱梁桥的高跨比分布在1/43.5~1/13,对于本连续轨道梁,选取梁高为2.2,2.3,2.4,2.5 m 进行优化分析。
3 工程概况及有限元模型
3.1 工程概况
该轨道梁为单箱单室等截面连续钢箱梁,主梁长度为40 m。由于单梁横向稳定性较差,故采用双线设计,由2片梁组成,中心间距3.7 m,2片梁间设置钢横联连接,提高其横向刚度与稳定性。单片梁宽度为0.7 m,梁高为H,顶板、底板及腹板厚度均为2 cm,钢箱梁内设置横隔板,横隔板间距4 m,厚1.8 cm,梁体统一采用Q345钢。横联结构见图1。
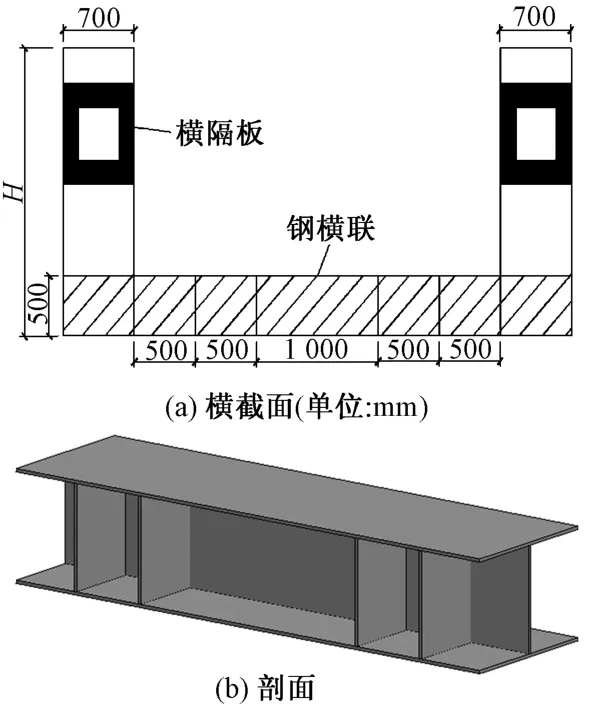
图1 横联结构
3.2 有限元模型
运用大型通用有限元软件ANSYS建立轨道梁模型[8]。采用Shell281壳单元对主梁、横隔板及横联进行模拟,使用共节点法建立横隔板与腹板、横联与主梁间的联系。全桥的外部边界条件采用一般3跨连续梁的约束条件。荷载考虑结构自重与列车活载,轻轨列车活载按GB 50458—2008《跨座式单轨交通设计规范》[9]所规定荷载施加。轨道梁有限元模型见图2。
假定其他设计参数不变,中跨跨度为40 m,改变梁高、边跨与中跨比,建立梁高 2.2,2.3,2.4,2.5 m 及边跨与中跨比为 0.6,0.7,0.8,0.9时组合形成的16种结构体系下的有限元模型,并分别对其力学特性进行分析计算。

图2 轨道梁有限元模型
4 结构优化结果分析
研究主跨40 m跨座式单轨交通连续钢箱轨道梁在不同梁高、不同边跨与中跨比组合时,活载作用下结构跨中最大挠度、竖向基频及最大梁端转角值,并通过对比分析确定最优梁高、边跨与中跨比。
根据GB 50458—2008,主跨40 m跨座式单轨交通连续钢箱轨道梁在列车活载作用下,主梁最大挠度、竖向基频及梁端转角的限值见表2。
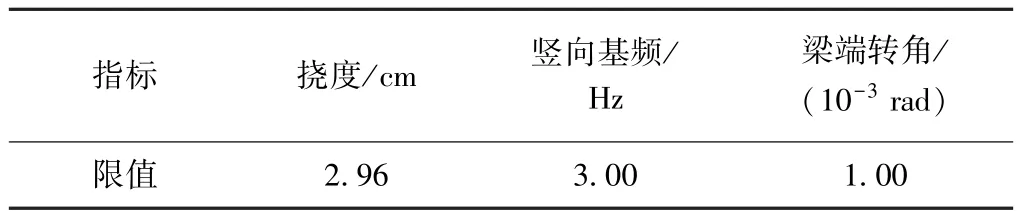
表2 主梁最大挠度、竖向基频及梁端转角限值
4.1 竖向位移约束下的优化分析
从分析结果中提取不同梁高、边跨与中跨比下结构体系的边跨、中跨跨中挠度,见表3、表4。

表3 边跨跨中挠度 cm

表4 中跨跨中挠度 cm
由表3、表4可知,当边跨与中跨比一定、梁高逐渐增大时,由于梁高增大导致主梁刚度增大,主梁在活载作用下边跨、中跨跨中挠度均减小,且梁高对主梁边跨、中跨挠度均有重要影响。以边跨与中跨比0.6为例,梁高由2.2 m增加到2.5 m时,主梁边跨、中跨跨中挠度均减小33.6%,其他情况亦同。
当梁高一定,边跨与中跨比逐渐增大时,由于边跨与中跨比逐渐增加,边跨长度逐渐增加,导致主梁整体刚度下降。在活载作用下,边跨、中跨跨中挠度均逐渐增大,且边跨与中跨比对边跨跨中挠度影响显著,对中跨跨中挠度影响较小。以梁高为2.2 m为例,边跨与中跨比由0.6增大到0.9,主梁边跨跨中挠度增加3.6倍,中跨跨中挠度增加16.7%。
将表3、表4中的数值与GB 50458—2008中挠度限值进行对比可以发现,除了梁高2.2 m、边跨与中跨比为0.9时边跨跨中挠度超出限值以外,其他情况均满足规范要求。
由以上分析可知:梁高、边跨与中跨比均对主梁边跨、中跨跨中挠度有重要影响。但规范GB 50458—2008中所规定的跨中挠度限值并不是影响梁高、边跨与中跨比取值的主要因素,即挠度不是控制本轨道梁结构设计的主要因素,可以作为梁高最小取值、边跨与中跨比最大取值的最终限制条件。
4.2 竖向基频约束下的优化分析
从分析结果中提取不同梁高、边跨与中跨比下结构的竖向基频,见表5。

表5 结构的竖向基频 Hz
由表5可见,当边跨与中跨比一定、梁高逐渐增大时,由于梁高增大导致主梁刚度增大,结构竖向基频增大,且梁高对结构竖向基频有重要影响。以边跨与中跨比0.6为例,梁高由2.2 m增加到2.5 m,结构竖向基频增加14.3%,其他情况亦同。
当梁高一定、边跨与中跨比逐渐增大时,由于边跨与中跨比逐渐增加,边跨长度逐渐增加,导致主梁整体竖向刚度下降,结构竖向基频逐渐减小,且边跨与中跨比对结构竖向基频影响较大。以梁高为2.2 m为例,边跨与中跨比由0.6增大到0.9,结构竖向基频减小29.9%,其他情况亦如此。
将表5中的数值与GB 50458—2008中竖向基频限值进行对比可以发现,在所有情况下,结构竖向基频均满足规范要求。
综上可知:梁高、边跨与中跨比均对结构竖向基频有重要影响。但规范中所规定的竖向基频限值同样不是影响梁高、边跨与中跨比取值的主要因素,即竖向基频不是控制本轨道梁设计的主要因素,可以作为梁高最小取值、边跨与中跨比最大取值的最终限制条件。
4.3 最大梁端转角约束下的优化分析
根据GB 50458—2008,连续轨道梁的联与联间通过安装指形板进行连接,以满足伸缩要求,而梁端转角对于指形板组件具有重要影响。梁端转角过大,使得指形板组件承受较大附加弯矩,造成指形板组件过早破坏。除此之外,还影响轨道平顺度及列车行驶的舒适性,严重时还会导致列车脱离轨道梁,影响行车安全。所以,在设计过程中对梁端转角的控制至关重要。
从分析结果中提取不同梁高、边跨与中跨比下主梁最大梁端转角,见表6。

表6 主梁最大梁端转角 10-3rad
由表6可见,边跨与中跨比一定时,随着梁高的增加,结构刚度增加,在活载作用下结构边跨、中跨挠度逐渐减小,导致结构最大梁端转角减小。且梁高对梁端转角影响显著,以边跨与中跨比0.6为例,梁高由2.2 m增加到2.5 m,梁端转角减小46.6%。
梁高一定时,随着边跨与中跨比的增大,结构刚度减小,边跨、中跨挠度逐渐增大,导致结构最大梁端转角逐渐增大,且边跨与中跨比对梁端转角影响更为显著。以梁高为2.2 m为例,边跨与中跨比由0.6增大到0.9,梁端转角增大81.2%。
将以上各情况下的最大梁端转角与规范中梁端转角限值对比可以发现,只有梁高为2.4,2.5 m、边跨与中跨比为 0.6,0.7,0.8时,最大梁端转角满足GB 50458—2008中的要求。可以认为 GB 50458—2008中规定的梁端转角是影响梁高、边跨与中跨比取值的主要因素。
当梁高为2.4,2.5 m、边跨与中跨比为 0.6,0.7,0.8时,结构变形、竖向基频以及梁端转角均满足规范要求时,为减轻自重、减少材料用量,从经济性角度考虑,选取2.4 m为最优梁高。
4.4 应力约束条件下的优化分析
在自重与活载组合作用下,当梁高为2.4 m、边跨与中跨比分别为0.6,0.7,0.8时,分析主梁边跨、中支点、中跨的控制截面应力及边跨与中跨比对控制截面最大拉、压应力的影响,控制截面最大拉、压应力见表7。

表7 控制截面最大拉、压应力 MPa
由表7可知:边跨与中跨比为0.8时,边跨最大应力大于中跨最大应力,边跨成为控制截面,受力不合理;边跨与中跨比为0.6,0.7时,中跨最大应力大于边跨最大应力,中跨为控制截面,受力较合理,故最优边跨与中跨比从0.6,0.7中选取;梁高为2.4 m,边跨与中跨比为0.6,0.7,0.8时,随着边跨与中跨比的增大,中跨最大拉、压应力逐渐减小,边跨与中支点截面最大拉、压应力逐渐增大,但均小于Q345钢材不考虑提高系数的容许应力值210 MPa,结构强度均满足规范要求。
由4.1节可知,边跨与中跨比为0.6时的边跨、中跨最大挠度均分别小于边跨与中跨比为0.7时的边跨、中跨最大挠度,故边跨与中跨比为0.6时更有利于结构变形,行车更加舒适。同时,边跨与中跨比为0.6时,结构材料用量相对于边跨与中跨比为0.7时减少8.3%,且施工难度与周期较小。
综合以上对比分析,从结构受力变形角度、经济性角度以及施工难易角度考虑,选取边跨与中跨比为0.6作为最优边跨与中跨比。
5 结论
1)本文运用直接网格搜索法原理以及双变量优化设计法,同时结合有限元软件ANSYS分析计算,对主跨40 m连续钢箱轨道梁进行优化设计,实践证明此方法简便、易行,可达到预期优化效果。
2)梁高、边跨与中跨比均对主梁边跨、中跨跨中挠度及结构竖向基频有重要影响。但结构挠度与竖向基频是主跨40 m连续钢箱轨道梁优化设计中控制设计的次要影响因素。
3)由优化设计结果可以看出,结构控制截面最大应力值远小于容许应力值。对于本文讨论的轨道梁结构,强度不控制设计。
4)通过对计算结果的分析对比可知,规范中规定的梁端转角是影响该主跨40 m连续钢箱轨道梁梁高、边跨与中跨比取值的主要因素。
5)通过对该主跨40 m跨座式交通连续钢箱轨道梁的优化设计可知:相比其他情况,当梁高为2.4 m、边跨与中跨比为0.6时,结构强度、刚度、竖向基频均满足规范要求,且结构变形及梁端最大转角较小,结构受力及变形最为合理,材料用量较小,最大限度地发挥材料的作用,避免了材料的浪费,且施工难度与周期较小。
综上所述,从结构力学特性、经济性以及施工难易角度考虑,经优化分析选取梁高为2.4 m、边跨与中跨比为0.6作为本主跨40 m连续钢箱轨道梁的推荐方案。

