隧道气囊在外压作用下的变形特性及试验验证
陈静,闫澍旺,孙立强,贺小青,郎瑞卿
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
随着地下空间的开发利用,城市地下铁路建设和运营中的安全问题日益突出。一些潜在的威胁如地下水渗漏、突发洪水、有毒气体等一旦发生,不仅影响隧道的正常施工和运营,而且会导致生命财产的损失,若灾害发生后不能得到有效的隔离,灾害的蔓延无疑会引起更大的经济损失和人员伤亡。例如,1992年芝加哥突发洪水,淹没了市中心隧道货运系统,迫使25万人撤离,耗时一个多月才将水从隧道抽出,耗资4 000万美元[1],若能及时将隧道阻隔,将会大大降低此次灾害的损失[2]。天津、上海等地区在修建地铁过程中,也出现了由地下水渗漏引起的安全问题[3-5]。大量地下水涌入隧道并流失,会造成地表地下水位的降低,从而对周围的建筑物的沉降产生影响,致使其开裂甚至倾斜。因此,针对隧道内的突发情况,亟需快速高效的临时性装置对危险源进行阻隔,避免灾害蔓延,以确保人民生命财产安全。隧道是较狭窄的地下环境,在发生危险时,抢救施工较为不便。目前常用的隔离方法是用现浇混凝土浇筑或砖砌体砌筑成挡墙进行阻隔抢险,此法不仅复杂耗时,无法应对严重且紧急的险情,并且险情消除后的拆除工程量大,同时,会在一定程度上损坏隧道壁。而采用充灌气囊作为隧道抢险挡水的临时性结构,具有质量轻、造价低、高效便捷的优点,其原理是增大气囊内压使其与隧道壁紧贴,利用与管壁之间的摩擦力堵住流体[6],将有毒气体或涌水渗漏阻隔在气囊的一端(简称“阻漏”)。目前,这种方法主要应用在中小直径的输气、输油管道中,在大直径的隧道中尚未应用。
有学者提出气囊可应用于隧道的分区中,模型试验主要致力于研究气囊的安装、膨胀以及阻挡流体的效果,尚未涉及气囊受侧压后的变形研究。如,Martinez等[7]针对隧道中突发的洪水或有毒气体,提出保护装置系统,该系统包含一个或数个气囊,安装固定在隧道顶部,险情一旦发生,便会触动开关机制,气囊可迅速膨胀,起到阻隔作用。Sosa等[8]进行了干、湿状态下,气囊材料与混凝土面的摩擦系数试验,并进行小比尺模型试验,气囊在摩阻力不足的情况下会产生滑移。Sosa等[9]进行了大比尺试验,将气囊安装在货运隧道人行道的上方,由于隧道形状存在较深的锐角,气囊与隧道壁不能完全贴紧,故在堵水过程中,凹凸角处有一定的漏水量,可通过泵将积水抽走。Eduardo等[10]用有限元方法模拟气囊的展开过程,包括气囊各边角的膨胀程度,研究不同模型模拟结果的差异,此模拟方法可用于预测实际气囊的展开过程。在中国,现阶段气囊主要应用在小直径的送水、送气管道的堵漏中,且研究范围主要限于应用和操作,尚未对气囊在隧道中的应用进行研究。邓华蛟[11]、曾强[12]介绍了气囊式封堵的基本原理、设备构造特点和应用方法,并在实际管道中取得了良好的效果。王祖灿[13]分析计算了各种封堵形式、材料对管道堵漏的效果,确定采用气囊制作封堵装置,分析了气囊与管壁直径的匹配关系以及是否滑动与摩阻力的关系。蒋贤荣等[14]在宁波某给水主管破裂,采取旁通临时应急供水管道,破裂处两端设置气囊封堵的方法,完成了抢修任务,恢复供水。王天英等[15]研制了自粘式快速封堵气囊,并进行了模拟试验和海上现场试验,说明其操作简便、安全可靠。李明[16]提出大口径的气囊对材料的抗拉强度要求更高,通过试验说明在外压压较小时,气囊堵水有很好的效果,增大外压至一定程度,气囊底部渗水挡水将失效。马弘毅[17]设计一种管口封堵装置,利用软件仿真模拟,得出橡胶气囊与管壁、封堵主体接触面的接触应力分布规律以及膨胀对密封性能的影响。张建等[18]提出球体薄壁压力容器的应力状态公式,对气枕式充气膜结构在不同外荷载作用下的受力状态进行分析。
以上研究均未涉及气囊在隧道中受到侧压后的变形和受力,这是决定气囊能否正常工作的关键问题。因为气囊属于膜结构,其抵挡外压的大小不仅由摩阻力决定,也取决于其形状变化的特点,并且因气囊四周受隧道管壁正向力约束,其变形和失效模式也不同于常规的膜结构。尤其对于隧道中的大直径气囊,由内压产生的材料拉力和需要阻挡的侧向力远远大于普通小直径气囊,其滑移失效后的危害也更加严重,因此,研究气囊在外压作用下变形、滑移的控制条件十分必要和关键,是气囊在隧道中使用的先决条件。
本文结合气囊在隧道中的边界条件,通过对隧道中的气囊进行受力分析,对其受荷前后的形状进行研究,得出自初始状态至滑移失效的整个过程中,其形状和内压随外压变化的关系,进而分析气囊滑移失效的模式、气囊长径比和初始压力对形状和内压变化的影响,以此判断气囊究竟能够抵挡多大的外压、在什么情况下阻挡失效。通过气囊缩比尺模型试验对理论公式进行验证,为气囊在工程上的应用提供了有效的理论依据。
1 气囊在外压作用下的变形特性
为研究置于隧道中气囊的变形特性和失效模式,分别建立二维模型和三维模型进行研究。由于二维模型概念简明,计算公式简洁,且结果一般偏于安全,故先研究二维模型情况下气囊的变形和受力特点,在此基础上利用相关概念建立三维模型,使之更加贴近实际情况。
1.1 二维模型情况
1.1.1 基本假定 为研究置于隧道中气囊的形状和受力特性以及工作机理,做如下假定:
1)隧道横截面为圆形。
2)气囊形状和变形是平面应变问题。
3)气囊为均质材料,忽略其刚度,且不考虑张力变化时气囊材料的拉伸或收缩量。
4)气囊一端受均匀压力作用。
5)气囊一端受荷载后,囊内气体满足气体状态方程
p0Va=p1Vb
(1)
式中:p0为气囊未受荷时内部的压强,kPa;Va为气囊内部压强为p0时的体积,m3;p1为气囊受荷之后的内部的压强,kPa;Vb为气囊内部压强为p1时的体积,m3。
1.1.2 气囊的初始形状及受力分析 气囊在内压作用下膨胀,进而与隧道壁贴紧,此时内压为p0,隧道直径为D,受隧道形状的约束,气囊的剖面由两段直线和两段曲线构成。直线段长L且紧贴隧道壁,受力分析如图1(a)所示,气囊在内压p0、隧道壁支持力pn及气囊拉力T0共同作用下平衡;曲线段与管壁脱离,其上任一点的受力分析如图1(b)所示[19],由受力平衡关系可知
(2)
式中:T0为初始状态气囊曲线段上任意一点的拉力;r(x)为纵坐标为x位置处的曲率半径;p(x)为纵坐标为x位置处的压强。
因空气重量可忽略不计,故各点压力p(x)=p0为定值,又因曲线段各点的拉力T0相等,故根据式(2)可知,r(x)为定值,又因曲线段与贴壁的直线段相切,故可知气囊两端的曲线段为半圆形。因此,气囊由两个半圆(Ⅰ区、Ⅲ区)和一个矩形(Ⅱ区)组成,气囊在隧道中的初始形状类似于药物胶囊,如图2所示。
取Ⅰ区半圆为研究对象,可知气囊上任意一点的轴向拉力为
T0=p0D/2
(3)
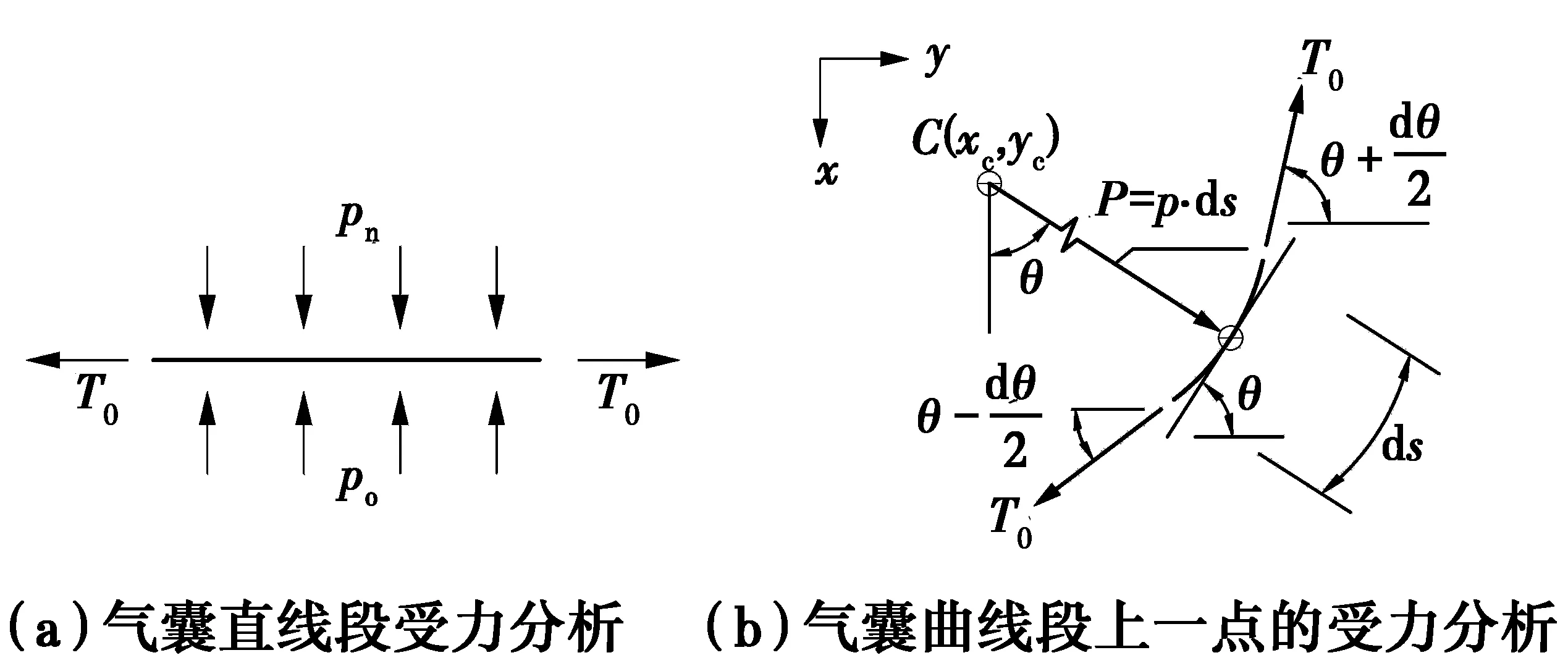
图1 气囊初始状态的受力分析Fig.1 Initial force analysis of the
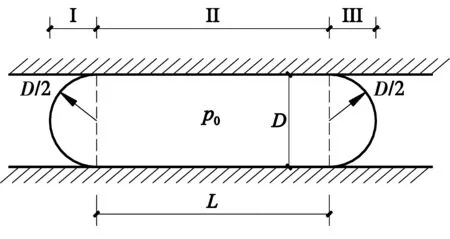
图2 气囊的初始剖面图Fig.2 Initial profile of the
1.1.3 气囊在外压作用下的形状及受力分析 当气囊一端受到外压pw作用时,假定摩阻力足够大,气囊不发生整体滑动,在外荷载、内部压力、隧道壁支撑反力和摩阻力共同作用下发生变形。气囊体积由Va变化到Vb,内部压力由p0变化至p1。在图3中,Ⅰ区为气囊左侧受荷端,Ⅱ区为气囊中间矩形部分,Ⅲ区为气囊右侧自由端。各区形状和受力的变化分析如下。
1)气囊受荷端的形状和受力分析 当气囊左端受到荷载pw时,气囊受荷端Ⅰ区曲线段外部压力增大,内外压差Δp减小,其上任一点形状r(x)如式(4)所示。内外压差沿隧道直径方向为定值,曲线段上拉力处相等,可知曲线段为一段圆弧,其长度为ly=R·θ,形状比半圆更为扁平,半径为R,大于变形前半径D/2,圆心角为θ。受荷前的Ⅰ区半圆除形成此时的圆弧ly外,其余的变为贴壁的直线段,长度为n,如图3中Ⅰ区所示。形状参数n、θ的大小与外压值有关,且随外压的增大而变化。
(4)
式中:pw为外部压强,kPa;θ为变形后袋子圆弧段的圆心角;R为变形后袋子圆弧段的半径,m;ly为变形后袋子Ⅰ区圆弧的长度,m;n为变形后袋子Ⅰ区每侧增加的直线长度,m;T1l为变形后气囊Ⅰ区圆弧的拉力,kN/m。
因为气囊材料只能承受拉力,T1l>0,由式(4)可知,当外力pw小于等于气囊内部压力p1时,圆弧的曲率半径为正,气囊能够保持其外凸的形状。当外部压力大于气囊内部压力,Ⅰ区圆弧段将内凹,此时没有外力可以平衡内凹曲线的张拉力,气囊形状不能保持,将会滑动失效。因此,在隧道中气囊能够正常工作的一个重要控制条件是外部压力必须小于内部压力,故可通过增大气囊内压以抵抗外压。
pw≤p1
(5)
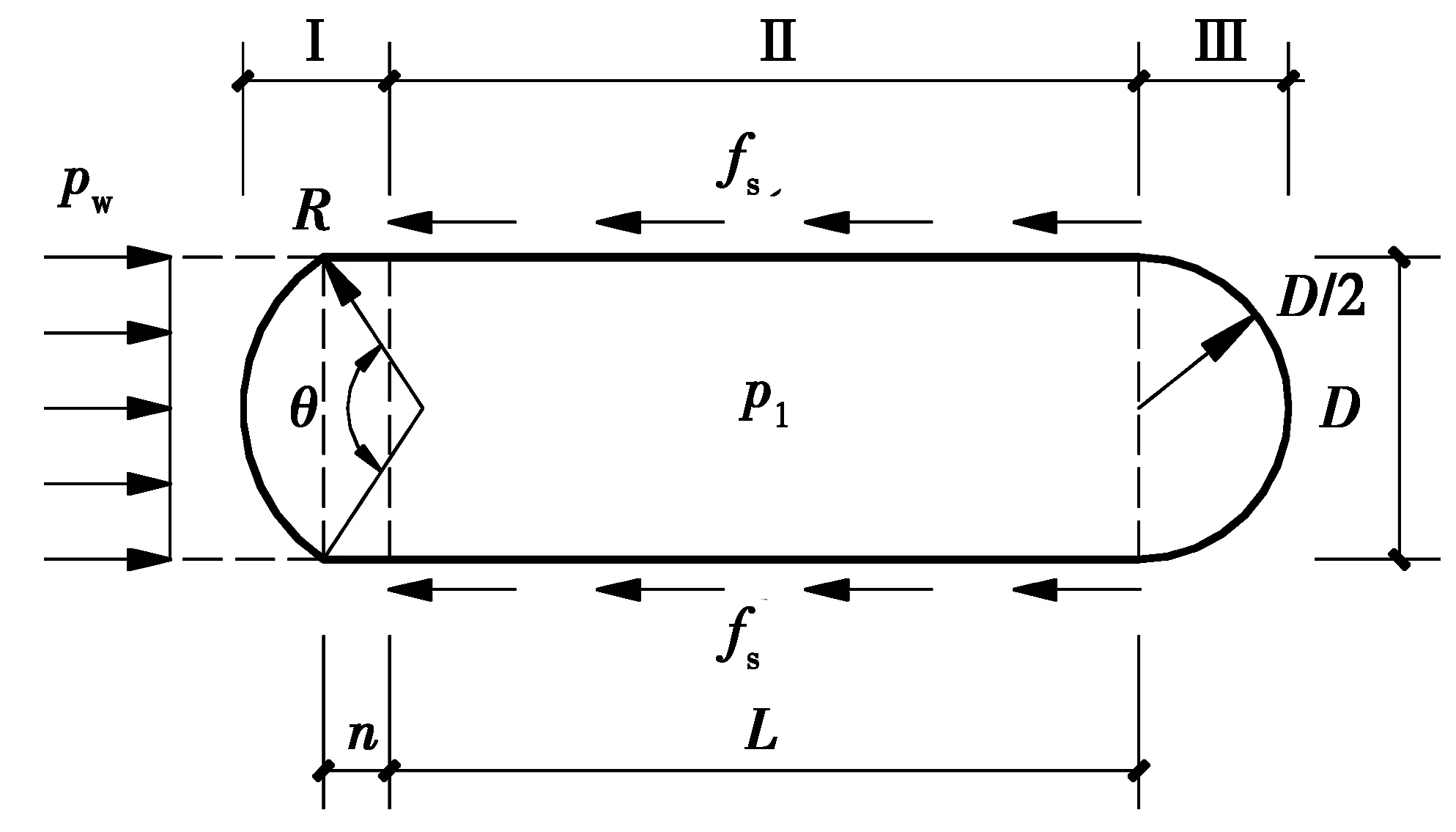
图3 气囊一端受荷后的形状和水平受力分析Fig.3 Shape and horizontal force analysis of the
2)气囊自由端的形状和受力分析 由于气囊材料不可伸长,当气囊内压由p0增加到p1时,自由端的形状仍为半圆,由式(2)可知,半圆上的张拉力随内压呈正比增加,受荷后自由端的拉力为
T1r=p1D/2
(6)
在外力pw作用下,受荷端的气囊内外压差减小,处于卸荷状态,材料张拉力降低;而自由端的张拉力随内压呈正比增大。贴壁直线段在左侧张力T1l、管壁摩阻力fs和右侧张力T1r的共同作用下保持平衡,各点的张拉力大小介于上述两端之间,直线段长度不变。故气囊自由端张力最大,为避免气囊张拉力过大导致材料破损,需使气囊受荷载后最大张拉力小于气囊材料的抗拉强度(式(7)),这是气囊正常工作的第二个控制要点,虽然,内压越大对于抵抗外压有利,但同时对材料强度要求更高。
T1r≤Ts
(7)
式中:T1r为受荷后气囊自由端的拉力,kN/m;Ts为气囊材料的抗拉强度,kN/m。
3) 确定受荷端的形状参数n、θ由以上分析可知,气囊受到外力作用后,只有受荷端的形状发生变化,直线段部分和自由端的形状均无变化,因此,只要确定受荷端的形状参数n、θ,即可得到在外压作用下气囊的准确形状。气囊形状变化与外压pw的大小一一对应,可由3个方程确定:变形前后气囊总长度相等、理想气体状态方程以及功能原理。
a.气囊周长在受荷前后不变
Ⅰ区初始长度为l1。
(8)
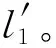
(9)
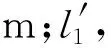
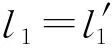
(10)
b.气囊内部气体满足理想气体状态方程
气囊受荷载前Ⅰ区面积为
(11)
受荷载作用后Ⅰ区面积由弓形和矩形组成,弓形面积可通过扇形面积和三角形面积之差求得。
(12)
(13)
(14)
A矩形=Dn
(15)
(16)
Ⅱ区和Ⅲ区的面积在受荷前后不发生变化。
(17)
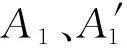
气囊变形前后满足气体状态方程式(1),将前文计算结果代入,可得
(18)
式中:Aa为气囊受荷载前的总面积,m2;Ab为气囊受荷载后的总面积,m2。
c.功能方程
在外压作用下,气囊的变形满足功能方程,即气囊体积变化与内压p1的乘积等于外力做的功。
(19)
式中:δ为气囊受荷中心点的位移。
根据几何关系
(20)
(21)
δ=0.5D-n-h
(22)
(23)
联立式(10)、式(18)和式(23)可计算得到受荷后的气囊形状参数n、θ,即可得到气囊在任意外压pw下的内压及形状。以气囊直径D=1 m,气囊直线段L=2 m,初始内压p0=10 kPa为例,当外压从零不断增大的过程中,气囊受荷端形状由半圆向扁平变化直至趋近于直线,θ值趋近于零,气囊变形到极限状态时,内压p1和外压pw同时达到最大值,如图4所示,可以看出,由于气囊内压的增大,能够抵挡的外压也超过了初始内压值。
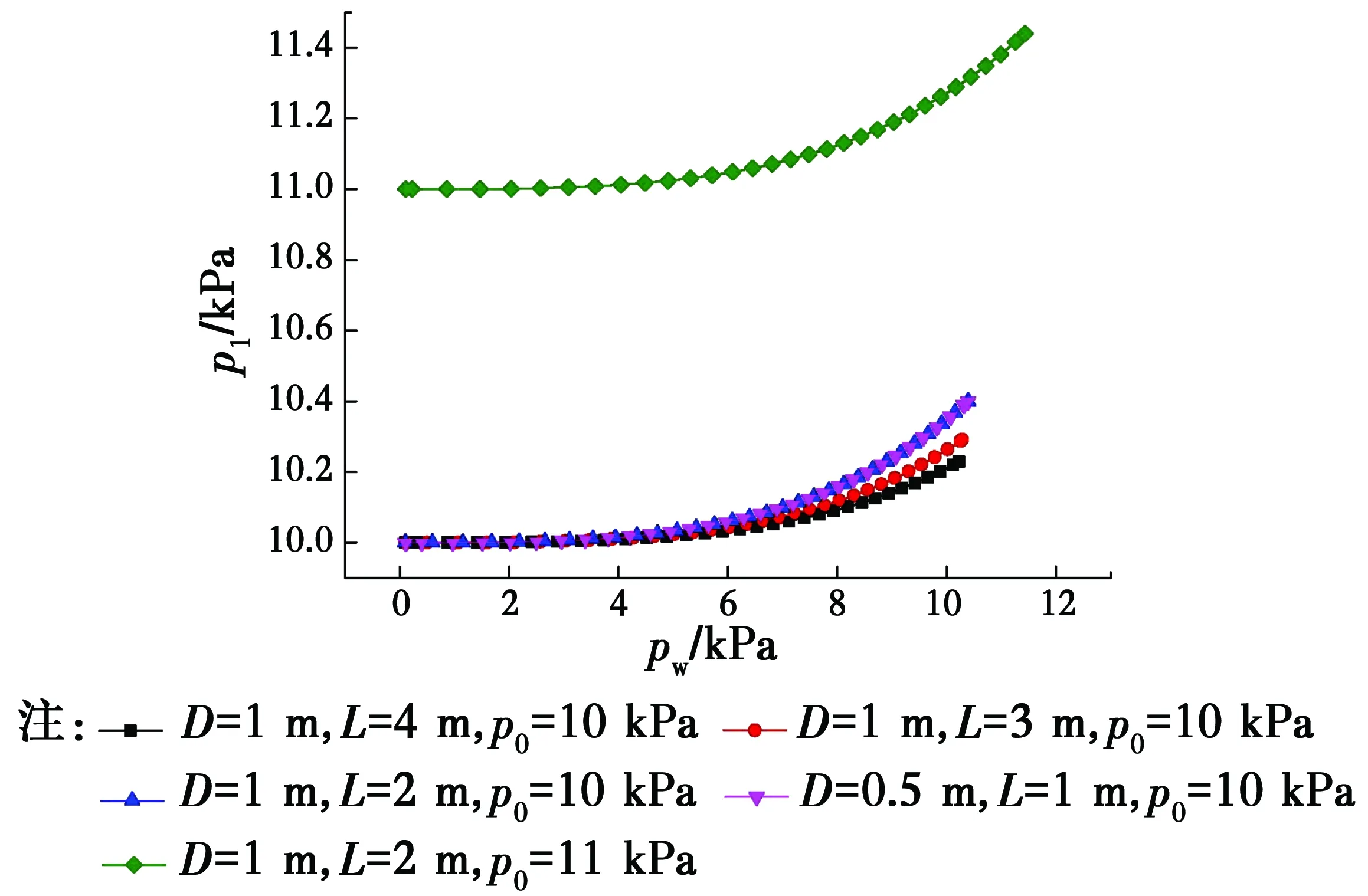
图4 气囊内压随外压变化规律Fig.4 Changes of internal pressure of airbag
改变气囊直径D、气囊直线段长度L以及初始内压p0,就可以得到不同形状、不同初始压力的气囊在外压增长过程中其形状和内压的变化规律。L/D=k表示气囊的长径比,令D=1 m,L=2、3、4 m,p0=10 kPa;D=1 m,L=2 m,p0=11 kPa;D=0.5 m,L=1 m,p0=10 kPa,将气囊内压和形状随外压的变化规律绘制于图4~图8。
由图4可知,当外荷载pw增大时,气囊的内压p1在初始内压p0的基础上增加,且不同气囊增长的规律类似。初始内压相同时,长径比越大,其内压随外压增长的幅度越小;当气囊的长径比相同,如D=1 m、L=2 m和D=0.5 m、L=1 m,气囊内压随外压的增长规律完全一致,曲线重合;内压增长意味着其可以抵抗的外压也在增长,但同时气囊材料的张拉力也在增大。
将外压和内压除以气囊初始内压,进行归一化处理,消除初始内压的影响。由图5可知,当气囊长径比相同时,即使初始内压不同,其内压随外荷载pw/p0增长规律完全一致。长径比越大,其内压随外压增长的幅度越小,A、B、C点分别为长径比k为4、3、2时气囊在极限状态时对应的外压和内压,也是外压和内压达到最大值的点。
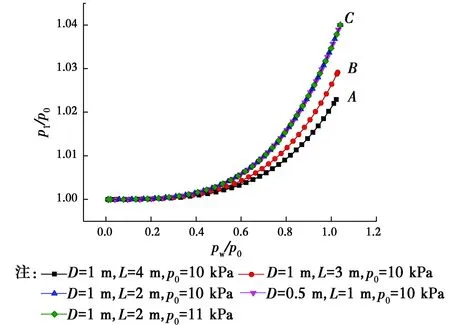
图5 归一化气囊内压随外压变化规律Fig.5 Changes of normalized internal pressure of airbag with external
不同长径比的气囊内压增长的幅度不同,将L/D=k代入式(18)可得气囊极限状态下内压与初始内压的比值p1ult/p0与长径比的关系,如式(24)和图6所示。
(24)
由图6可知,k值越大,由外侧压力导致的气囊内压的增长越不明显,图中A、B、C点分别对应于图5中长径比k为4、3、2的气囊。
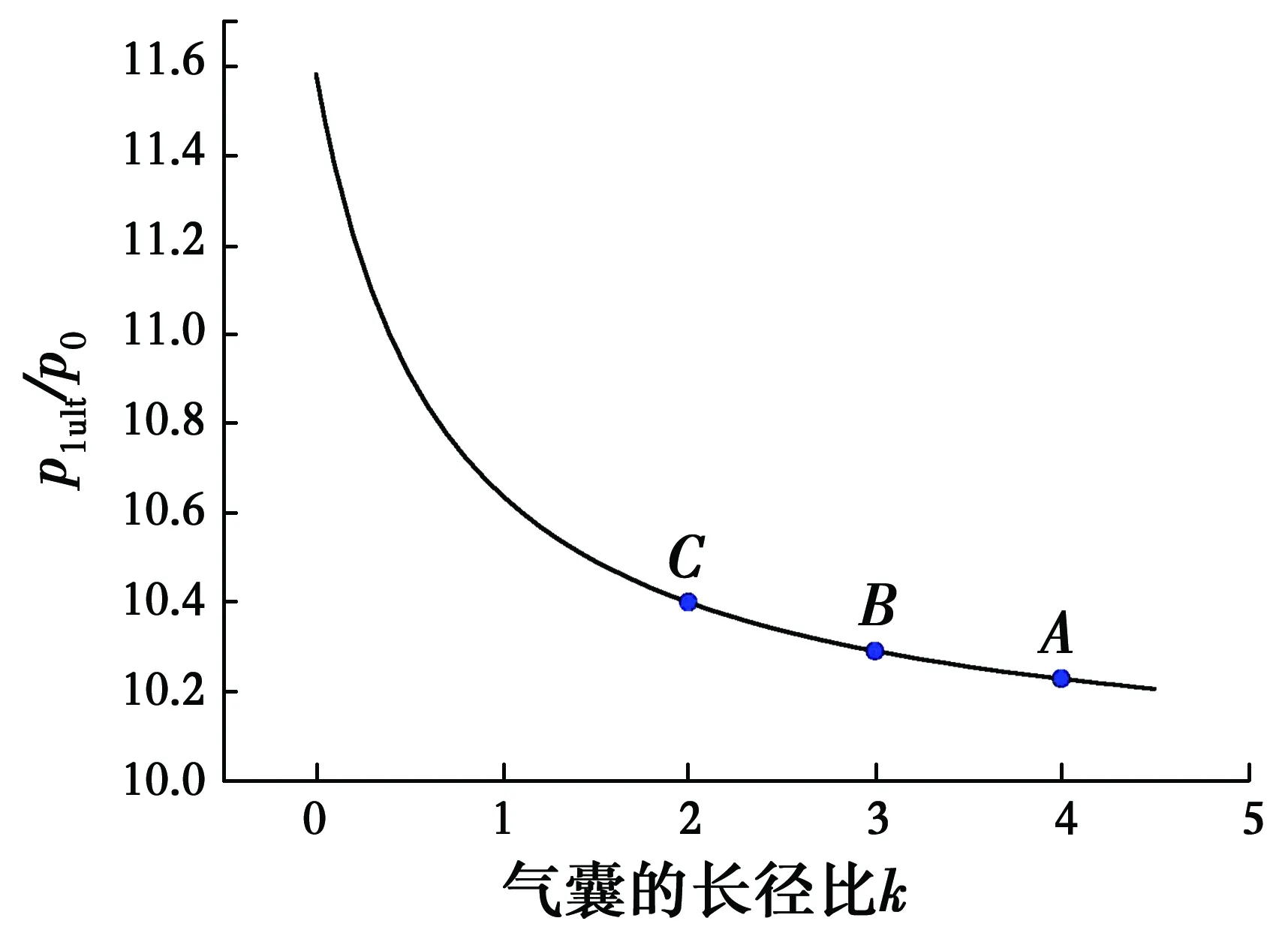
图6 p1ult/p0-k曲线
由图7可知,随着外压增大,受荷端圆弧的圆心角θ由π变化至零,受荷端的曲线变成一条直线。相同长径比的气囊,其变化曲线完全重合,不同长径比的气囊θ值变化至零时所需的外压不同。
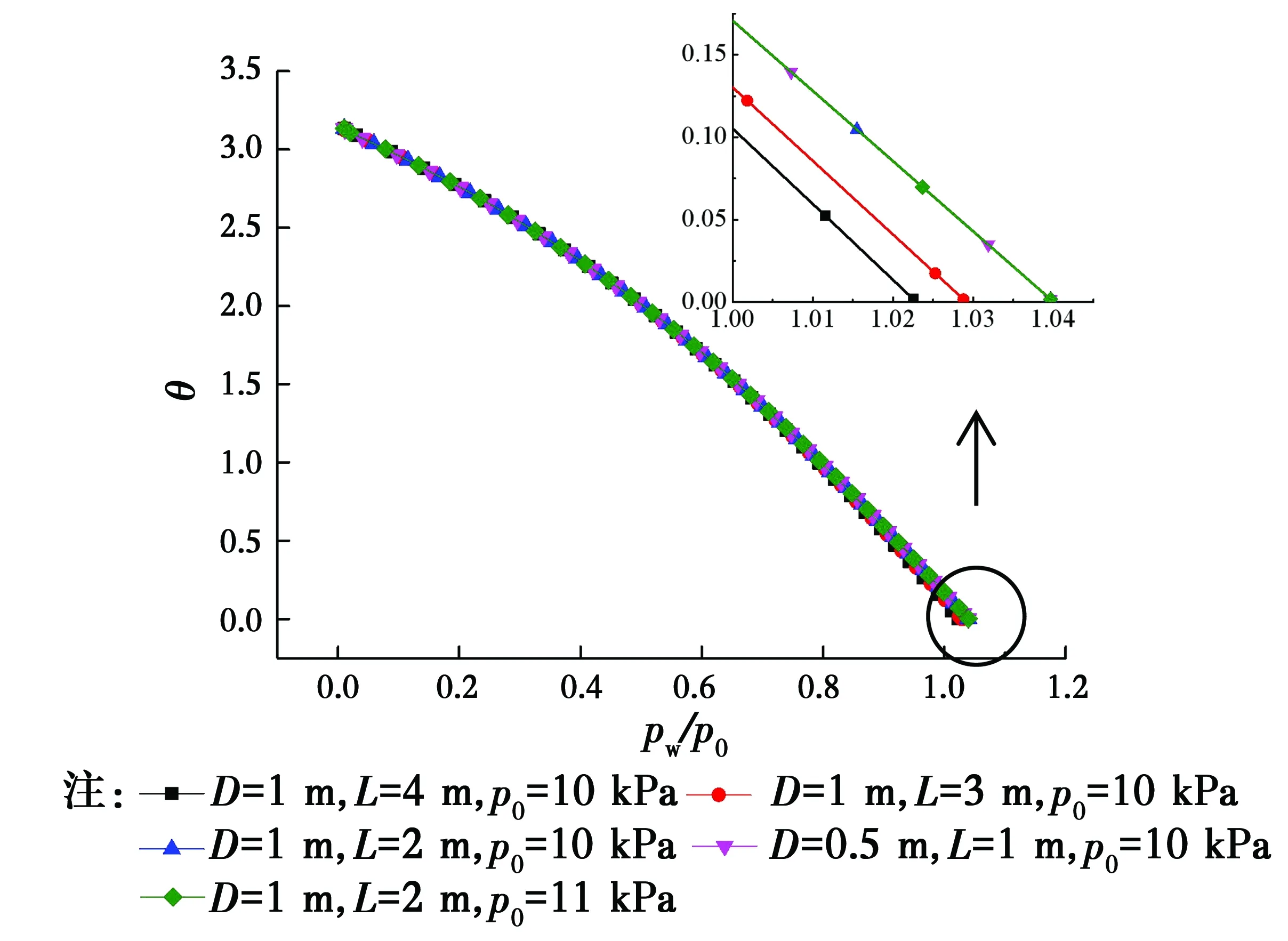
图7 气囊形状参数θ随外压变化规律Fig.7 Changes of the shape parameter θ of the airbag with the external
由图8可知,随着外压增大,受荷端曲线增加的直线段n逐渐增大,当气囊直径D相等时,不论气囊直线段长度、初始内压为何值,n变化规律一致;直径越大,n值增大的越明显。
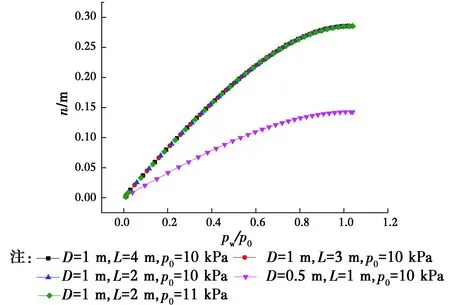
图8 气囊形状参数n随外压变化规律Fig.8 Changes of the shape parameter n of the airbag with the external
1.1.4 气囊所受外力与最大静摩阻力 在外力作用下,气囊所受的静摩阻力与外力平衡,如图3所示。以上关于气囊的变形分析也是基于摩阻力足够大的前提,为避免因摩阻力不足而导致滑动,需使其最大静摩阻力大于外力。
由气囊工作状态时的形状特性可知,气囊的内压和直线段长度随着外荷载的增大而逐渐增大,因此,最大静摩阻力也随外压增大而变化,其表达式如式(25)所示,气囊所受外力如式(26)所示。
Fs=2μp1(L+n)
(25)
Fw=pwD
(26)
式中:Fs为气囊与隧道壁间的最大静摩阻力,kN;Fw为气囊所受外力,kN。
由式(25)可知,气囊与隧道壁间的最大静摩阻力与气囊初始直线段长度L和摩擦系数μ紧密相关。令D=1 m,L=2 m,μ=0.3;D=1 m,L=3 m,μ=0.3;D=1 m,L=2 m,μ=0.2,求得在外力增大导致形状变化的过程中,最大静摩阻力的变化,如图9所示。
由图9可知,在气囊受荷端圆心角从π变化至零的过程中,最大静摩阻力和外力不断增大。根据两者的曲线关系,可判断气囊滑移失效的原因:当最大静摩阻力一直大于外力时,气囊是因为外压接近于内压导致的受荷端变形而失效;当最大静摩阻力小于外力时,气囊受荷端未完全变形时就会因摩阻力不足产生滑移,这是气囊滑移失效的两种模式。据此可以选择长度和摩擦系数合适的气囊,以确保气囊摩阻力可以满足外力的需要。
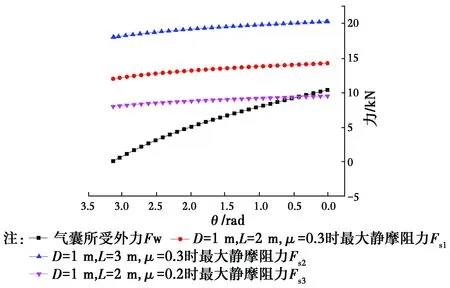
图9 外力和最大静摩阻力的变化规律Fig.9 Changes of external force and maximum static friction
1.2 三维模型情况
1.2.1 基本假定 以三维立体模型来进行研究分析,所用假定同二维模型。
1.2.2 气囊的初始形状及受力分析 气囊在内压作用下膨胀后与隧道壁贴紧,其左右两端(Ⅰ区、Ⅲ区)为半球体,中间部分(Ⅱ区)为圆柱体,气囊的初始充气压力为p0,如图10所示。
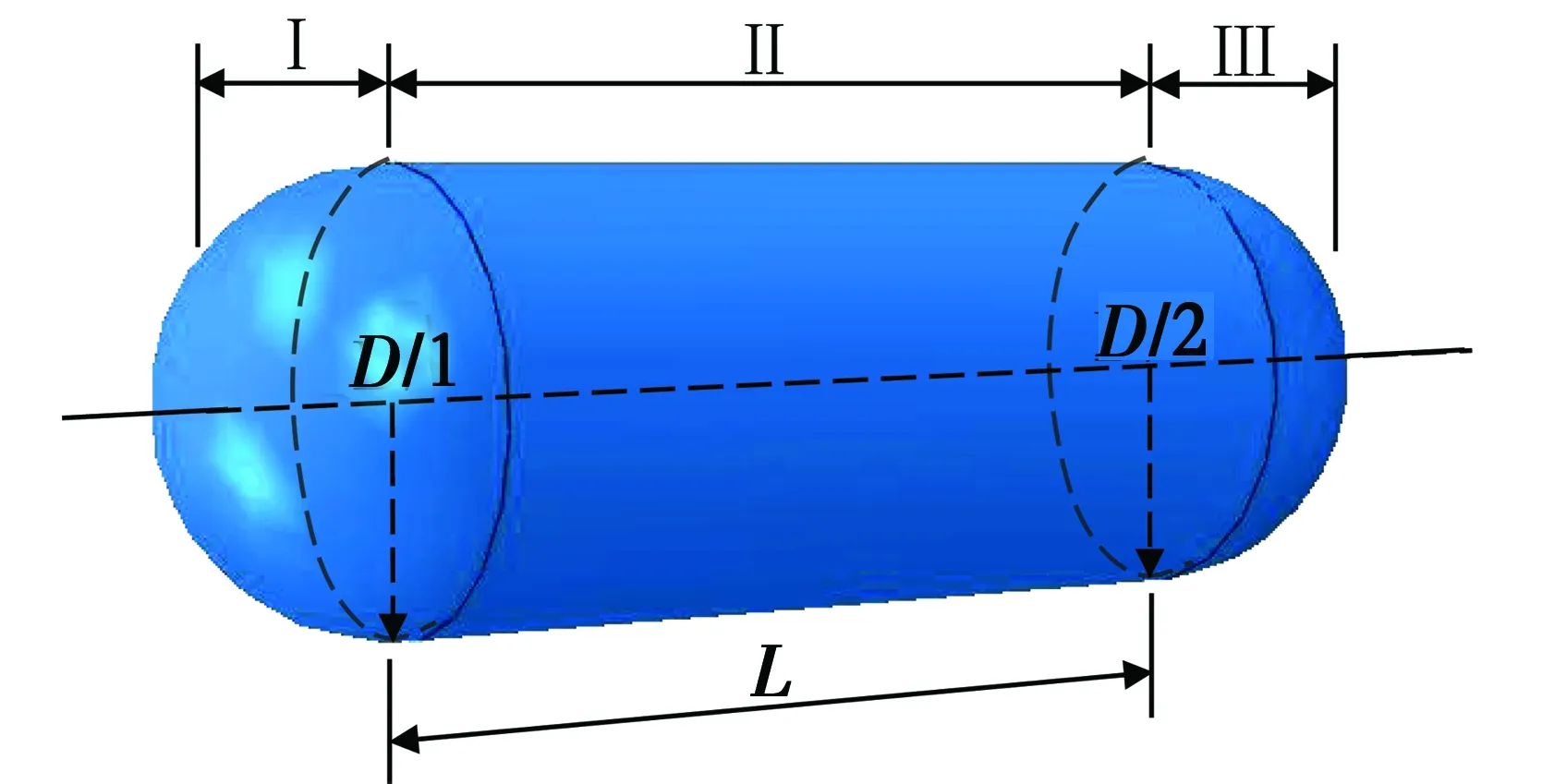
图10 气囊的初始形状Fig.10 Initial shape of the
以Ⅰ区半球为研究对象,内压在水平方向上的投影合力等于拉力与截面周长的乘积(式(27)),因此,气囊的轴向拉力为
T0·πD=p0·0.25·πD2
(27)
T0=0.25p0D
(28)
对比式(3)可知,利用三维模型分析得到的气囊拉力是二维分析时所得拉力的一半,所以,依据二维模型计算结果来选择气囊材料偏于安全。
1.2.3 气囊在外压作用下的形状及受力分析
1)气囊受荷一端和自由端的形状 当气囊Ⅰ区受到荷载pw时,在外荷载、内部气压力、隧道壁支撑力和摩阻力的共同作用下发生变形,体积由Va变化到Vb,内部压力由p0变化到p1。受荷端(Ⅰ区)在外压作用下,处于卸荷状态,形状变为球缺和圆柱体的组合,球缺的半径为R,圆心角为θ,圆柱体高度为n,如图11所示。而气囊Ⅱ区圆柱体、Ⅲ区自由端的形状不发生变化,Ⅲ区仍为半球,但张力随内压增大呈正比增大为T1r,成为拉力的控制条件。
T1r=0.25p1D
(29)
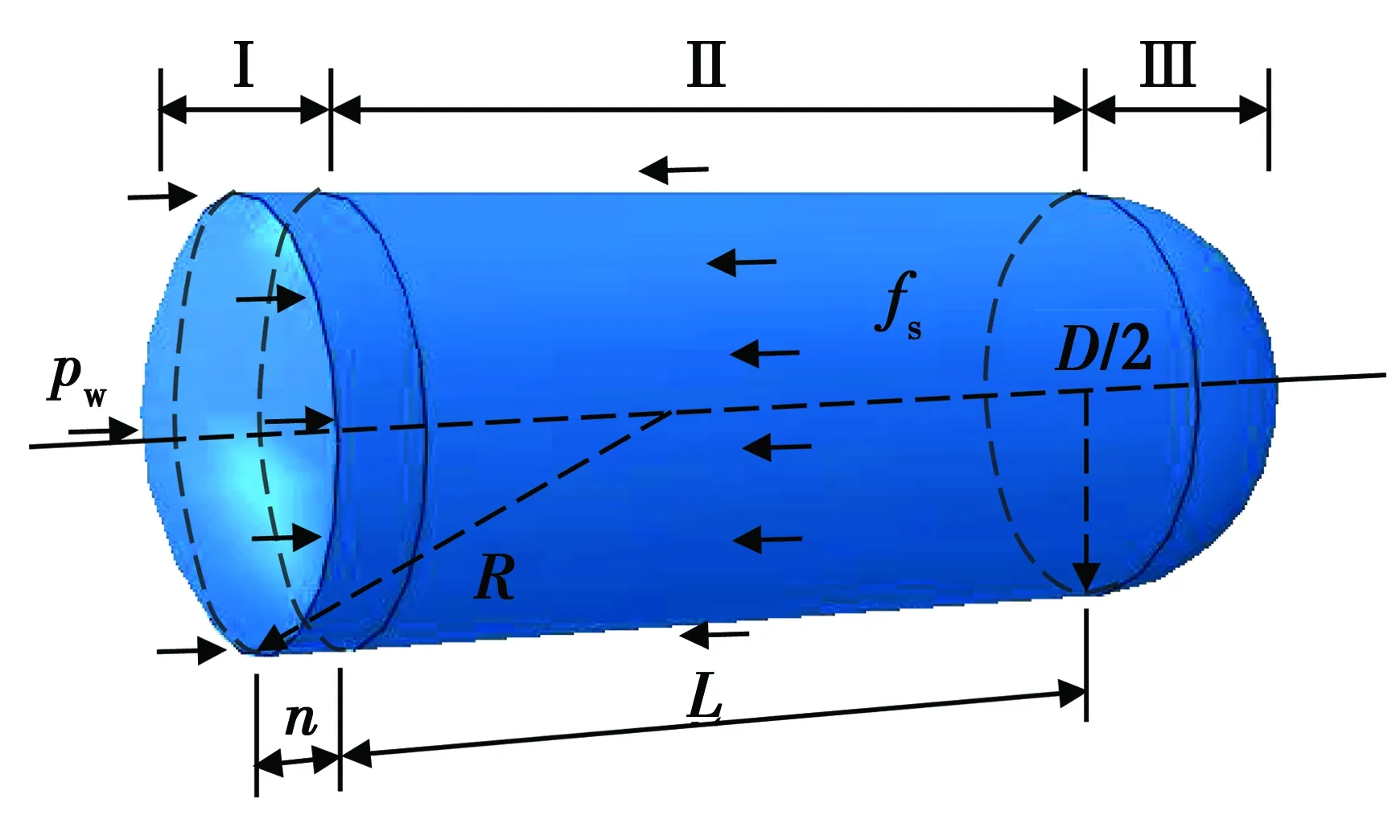
图11 气囊一端受荷后的形状和水平受力分析Fig.11 Shape and horizontal force analysis of the airbag after
2)确定受荷端的形状参数n、θ气囊受外压后,仅Ⅰ区形状发生变化,贴壁段(Ⅱ区)和右端自由端(Ⅲ区)的形状不变,因此,只要确定受荷端的形状参数n、θ,即可得到在外压作用下气囊的准确形状。气囊形状变化与外压pw的大小一一对应,可由3个方程确定:变形前后气囊总表面积相等、理想气体状态方程以及功能原理。
a.受荷前后气囊表面积相等 Ⅰ区初始形状为半球形,表面积S1为
(30)
(31)
(32)
S球缺=2πR(R-m)
(33)
S圆柱体=πDn
(34)
(35)
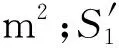
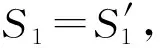
(36)
b.受荷前后气体满足理想气体状态方程 气囊受荷载前Ⅰ区体积V1为
(37)
(38)
受荷载作用后Ⅰ区体积由球缺和圆柱体组成。
(39)
(40)
(41)
(42)
(43)
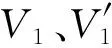
c.功能方程 在外压作用下,气囊的变形满足功能方程,即气囊体积变化与内压p1的乘积等于外力做的功。
(44)
δ=0.5D-n-h=
(45)
(46)
联立式(36)、式(43)和式(46)可计算得到受荷后的气囊形状参数n、θ,即可得到气囊在任意外压pw下的内压以及形状。
改变气囊直径D、气囊直线段长度L以及初始内压p0,可得到不同形状、初始状态的气囊在外压增长过程中其形状和内压的变化规律。L/D=k表示气囊的长径比,令D=1 m,L=2、3、4 m,p0=10 kPa;D=1 m,L=2 m,p0=11 kPa;D=0.5 m,L=1 m,p0=10 kPa,将气囊内压和形状随外压变化规律绘制于图12~图16。
由图12、图13可知,三维模型内压随外压变化规律同二维模型,但在同一种工况、同一外压时,三维模型内压增长幅度略小于二维模型。
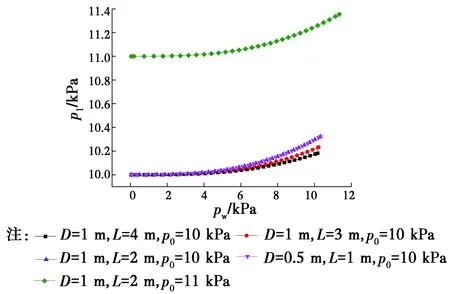
图12 气囊内压随外压变化规律Fig.12 Changes of internal pressure of
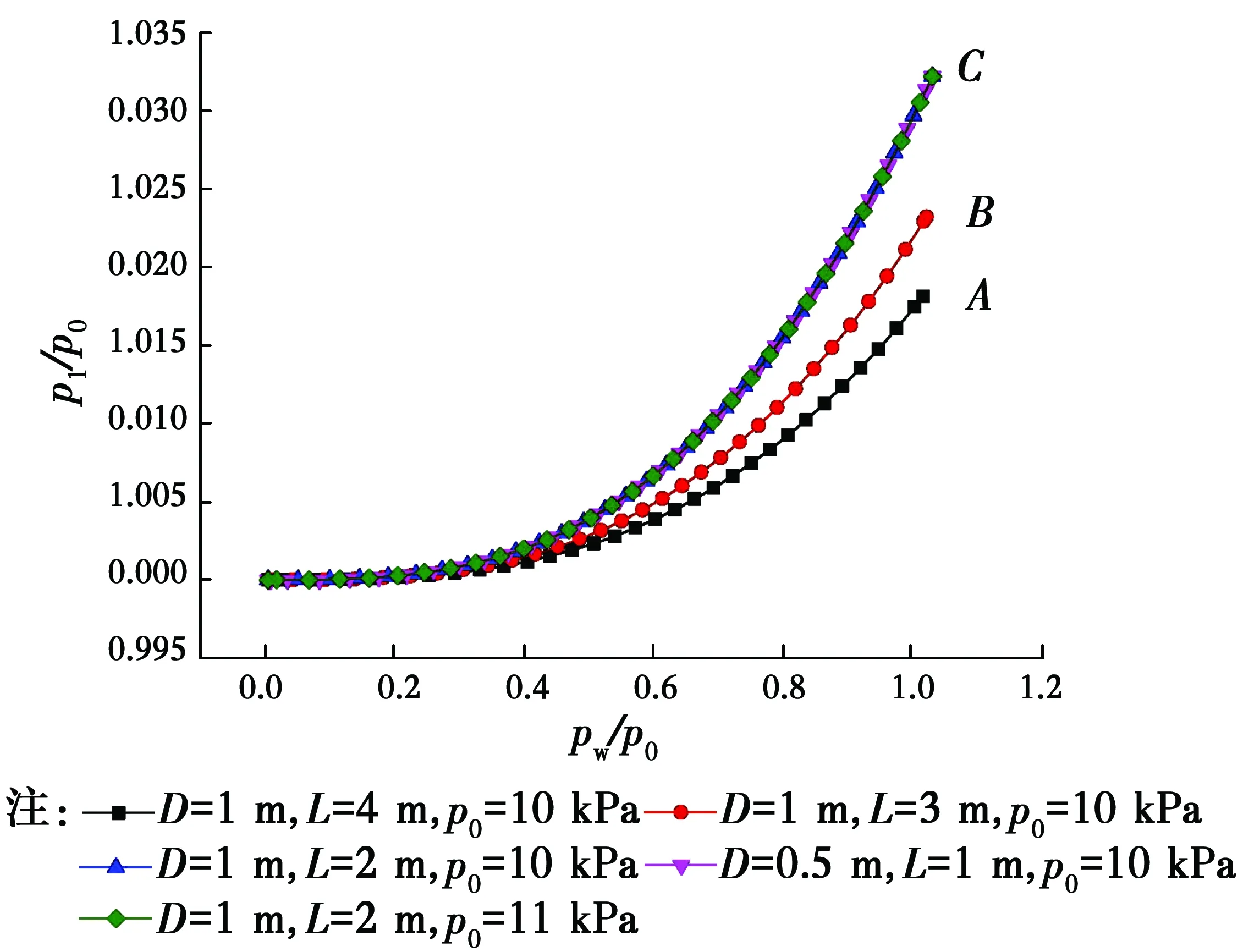
图13 归一化气囊内压随外压变化规律Fig.13 Changes of normalized internal pressure of
将长径比L/D=k代入式(43)可得气囊极限状态下内压与初始内压的比值p1ult/p0与长径比的关系,如式(47)和图14所示。
(47)
由图14可知,k值越大,外侧压力导致的气囊内压的增长越不明显,图中A、B、C点分别对应于图13中长径比k为4、3、2的气囊。
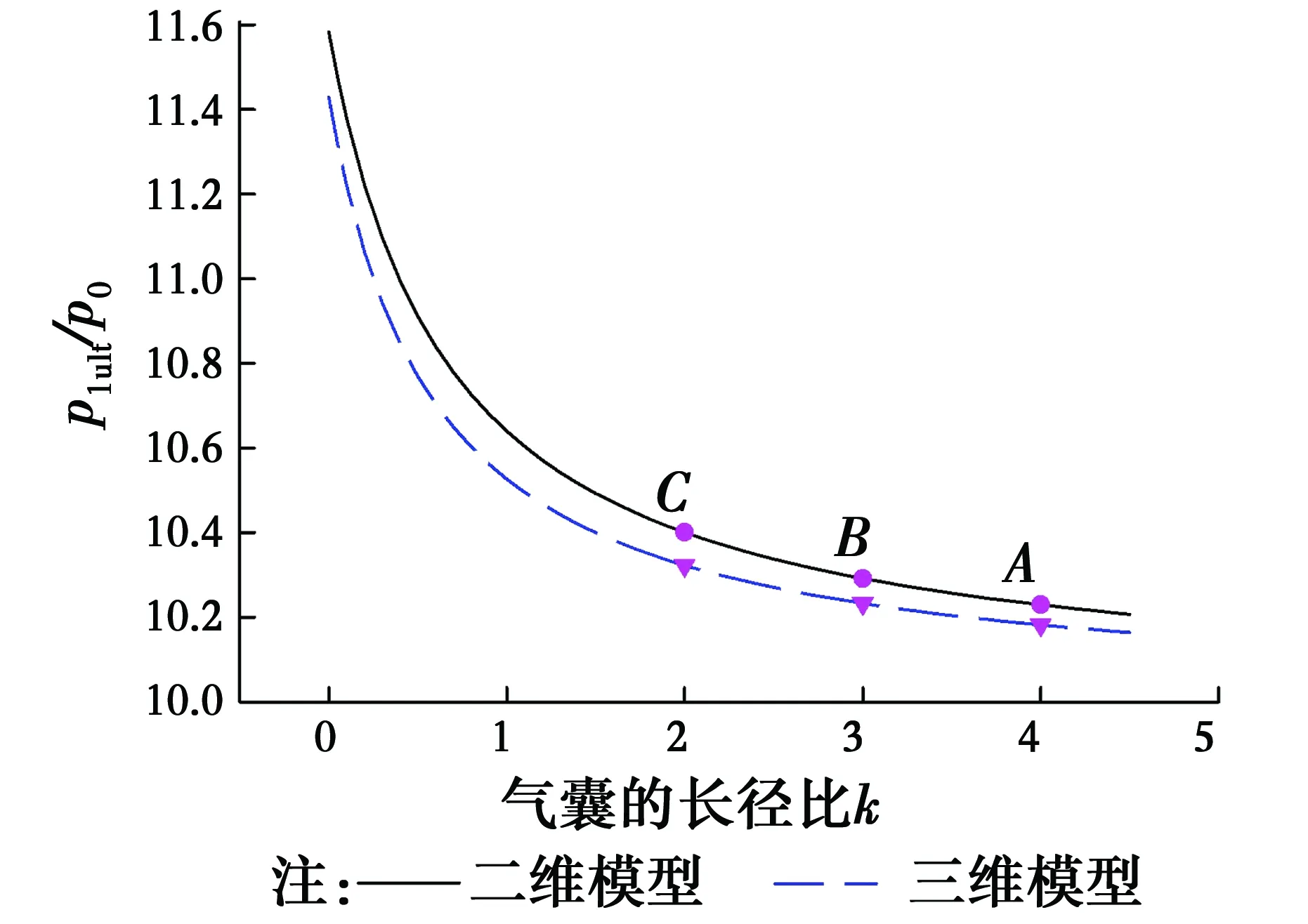
图14 p1ult/p0-k曲线
由图15可知,三维模型受荷端圆弧的圆心角随外压变化的规律同二维模型,对应同一个θ时,三维模型计算结果所需要的外压较小。
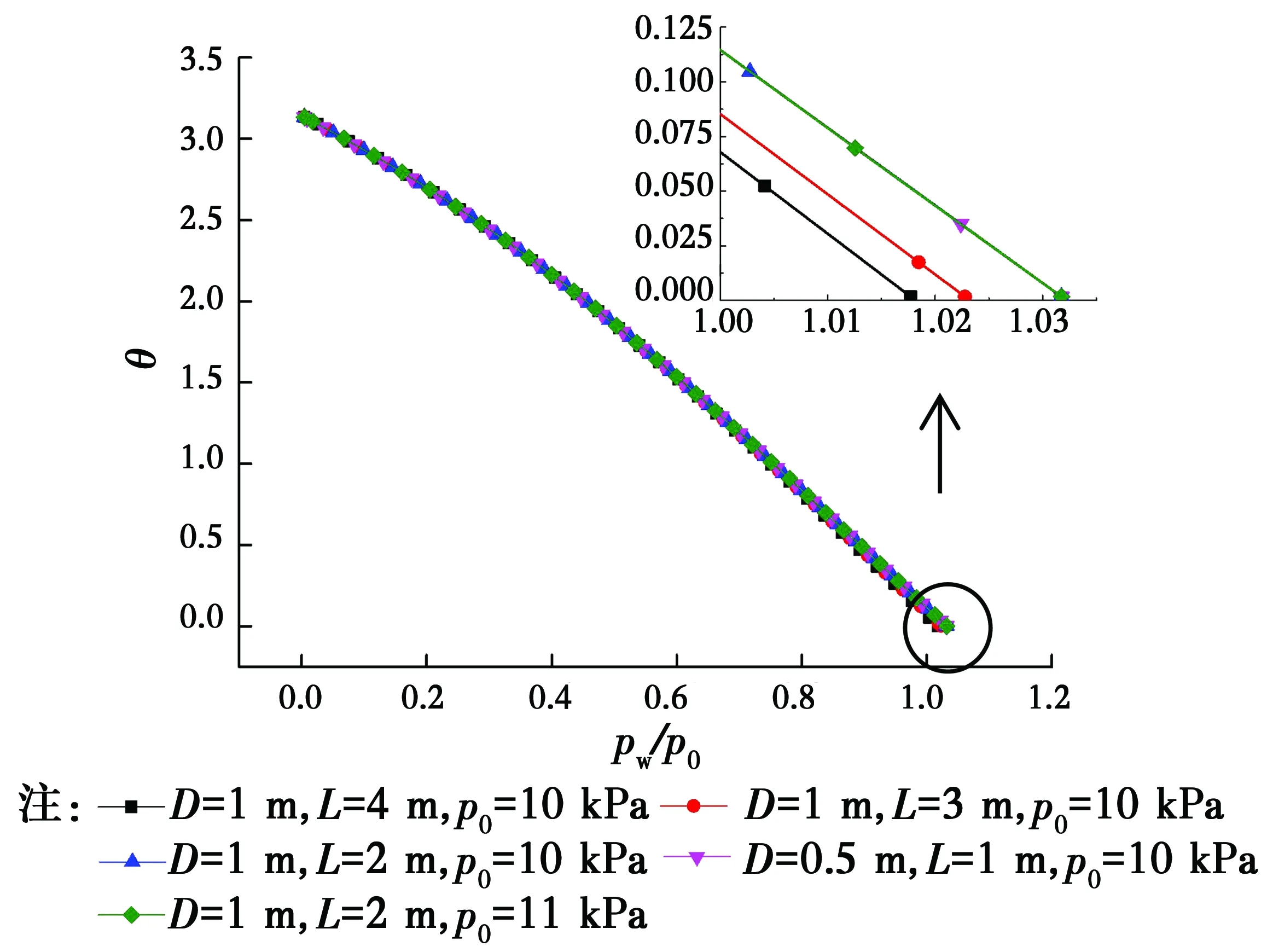
图15 气囊形状参数θ随外压变化规律Fig.15 Changes of the shape parameter θ of the airbag with the external
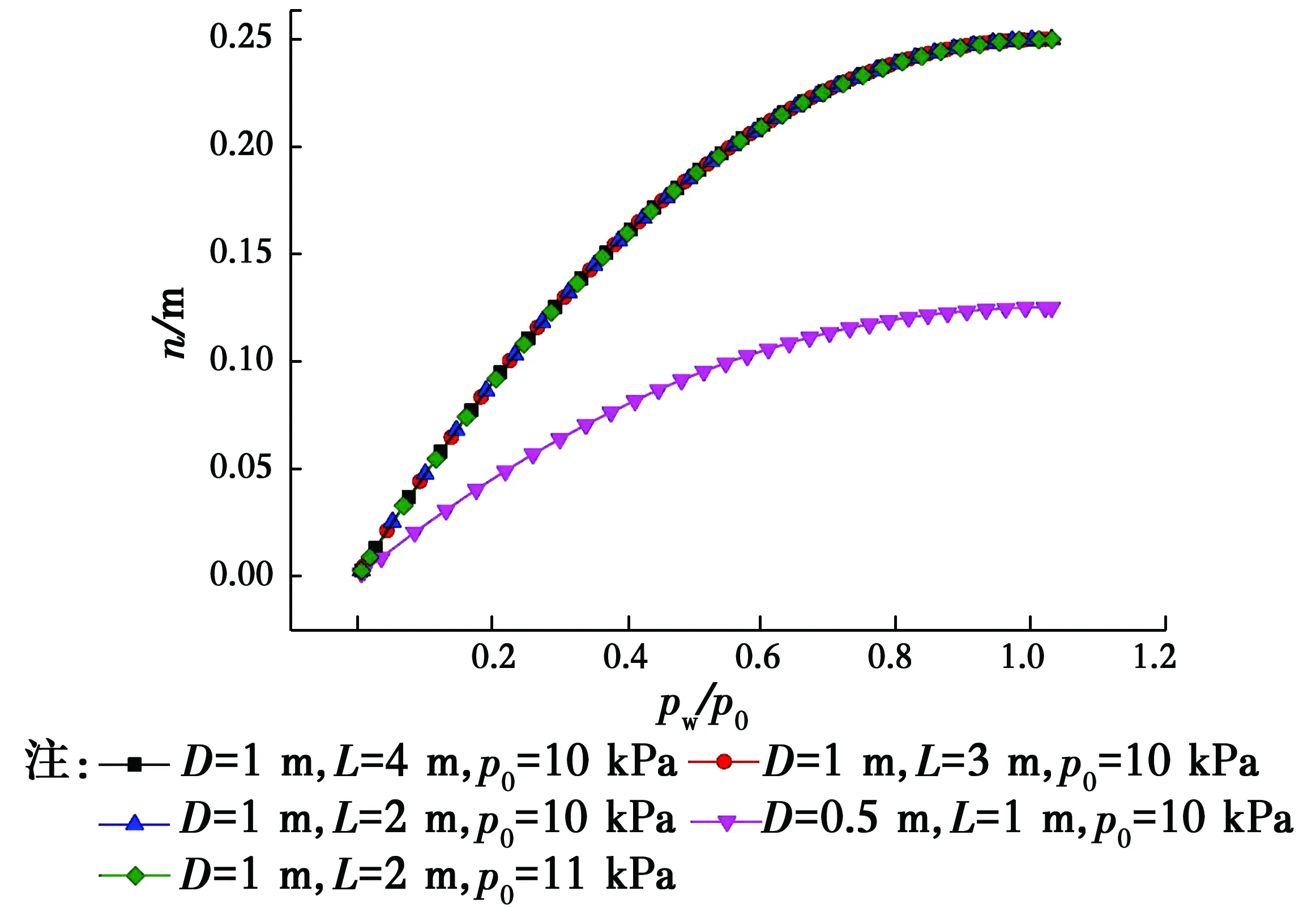
图16 气囊形状参数n随外压变化规律Fig.16 Changes of the shape parameter n of the airbag with the external
由图16可知,三维模型受荷端曲线增加的直线段n随外压变化规律同二维模型,对应同一个外压时,三维模型计算结果n较小。
由图12~图16可知,三维模型计算得到的气囊内压和形状变化规律与二维模型相同,在同一外压下,其计算得到的内压较小,形状参数θ、n也较小。
1.2.4 气囊所受外力与最大静摩阻力 在外力作用下,气囊所受的静摩阻力与外力平衡,如图11所示。以上关于气囊的变形分析也是基于摩阻力足够的前提,为避免气囊因摩阻力不足而导致滑动,需使其最大静摩阻力大于外力。最大静摩阻力随外压增大而增大,其表达式如式(48)所示。气囊所受外力如式(49)所示。
Fs=μp1(L+n)πD
(48)
(49)
对比式(25)、式(26)和式(48)、式(49)可知,在同一内部压力下,三维方法算出的气囊能够抵挡的外压更大,近似于二维算法的两倍。
由式(48)可知,气囊与隧道壁间的最大静摩阻力与气囊初始直线段长度L和摩擦系数μ紧密相关。令D=1 m,L=2 m,μ=0.3;D=1 m,L=3 m,μ=0.3;D=1 m,L=2 m,μ=0.2,求得气囊在外力增大导致形状变化的过程中,最大静摩阻力的变化,如图17所示。
对比图9和图17,以工况D=1 m,L=2 m,μ=0.2为例,用三维模型计算得到最大静摩阻力一直大于外力,说明用三维模型气囊可抵挡更大的外力,二维模型偏于保守。
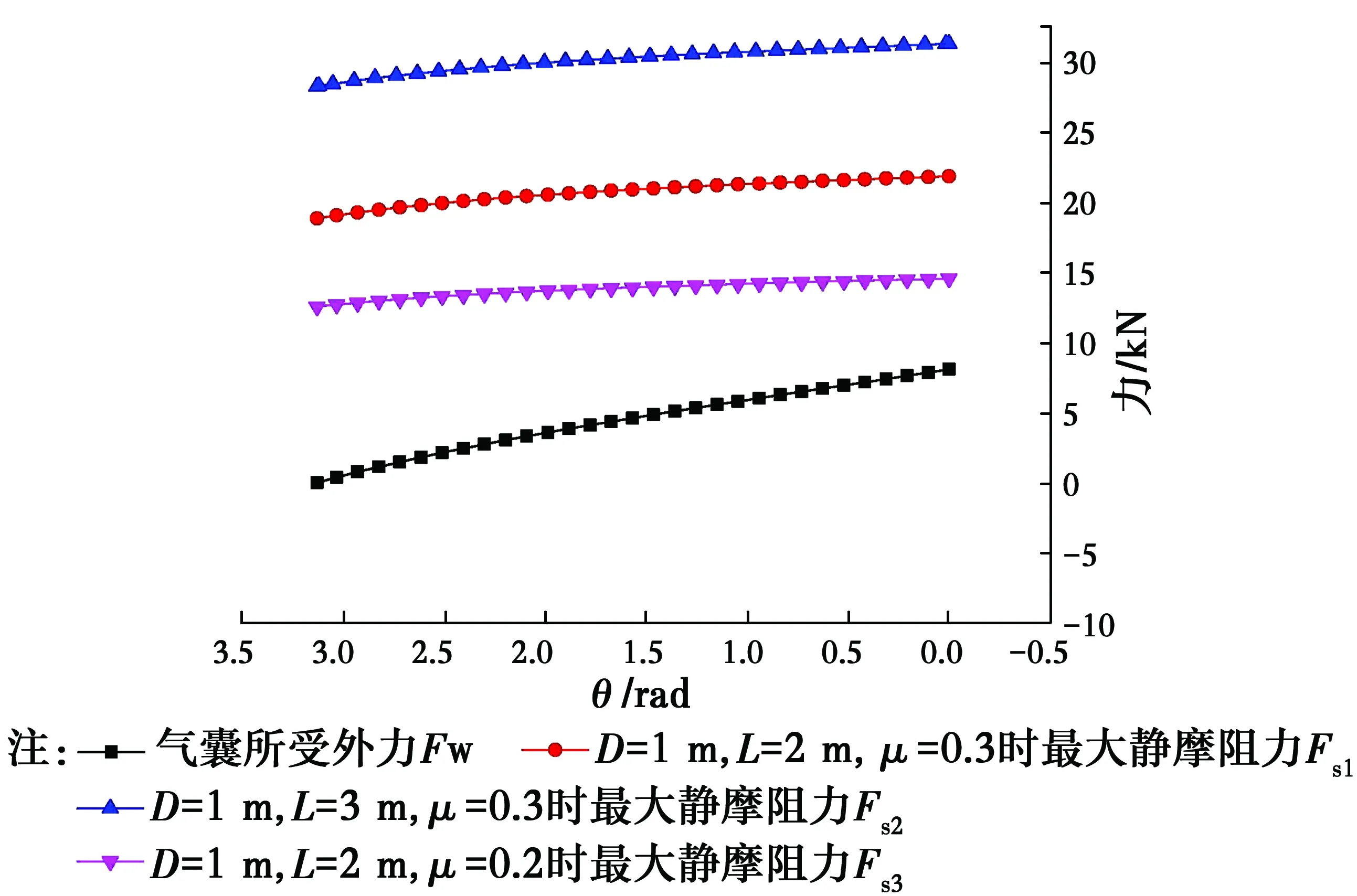
图17 外力和最大静摩阻力的变化规律Fig.17 Changes of external force and maximum
对比二维模型和三维模型,二维模型计算得到的气囊拉力是三维结果的2倍,内压p1增长量比三维模型稍大,且能够抵挡的外力是三维的一半。故使用二维模型用于设计和计算偏于安全,使用三维模型更接近实际,在设计中宜考虑乘以安全系数。
2 模型试验
2.1 试验介绍
气囊阻漏的工作条件和失效模式对于不同直径的气囊都是适用的,为探究气囊受荷之后形状以及内压随外压变化的规律,验证气囊阻漏失效的模式和控制条件,以天津某地铁隧道为原型,进行缩比尺试验(9∶1)。隧道实际直径为5.5 m,模型直径为0.61 m,长2.5 m,一端封闭并与加压系统相连,以提供均匀侧压力,一端敞口,如图18所示。气囊选用PVC膜材料,其在张拉力变化时的伸长和缩短十分微小,可忽略不计。气囊外径等于模型隧道内径,以便在充气后与隧道壁完全贴合,气囊直线段长度L=0.89 m,与模型隧道壁的摩擦系数μ=0.3。空气压缩机用以提供气囊内压和侧向气压;储气罐用以贮存空气,调节压力值;压力表用来测量内压和外压。
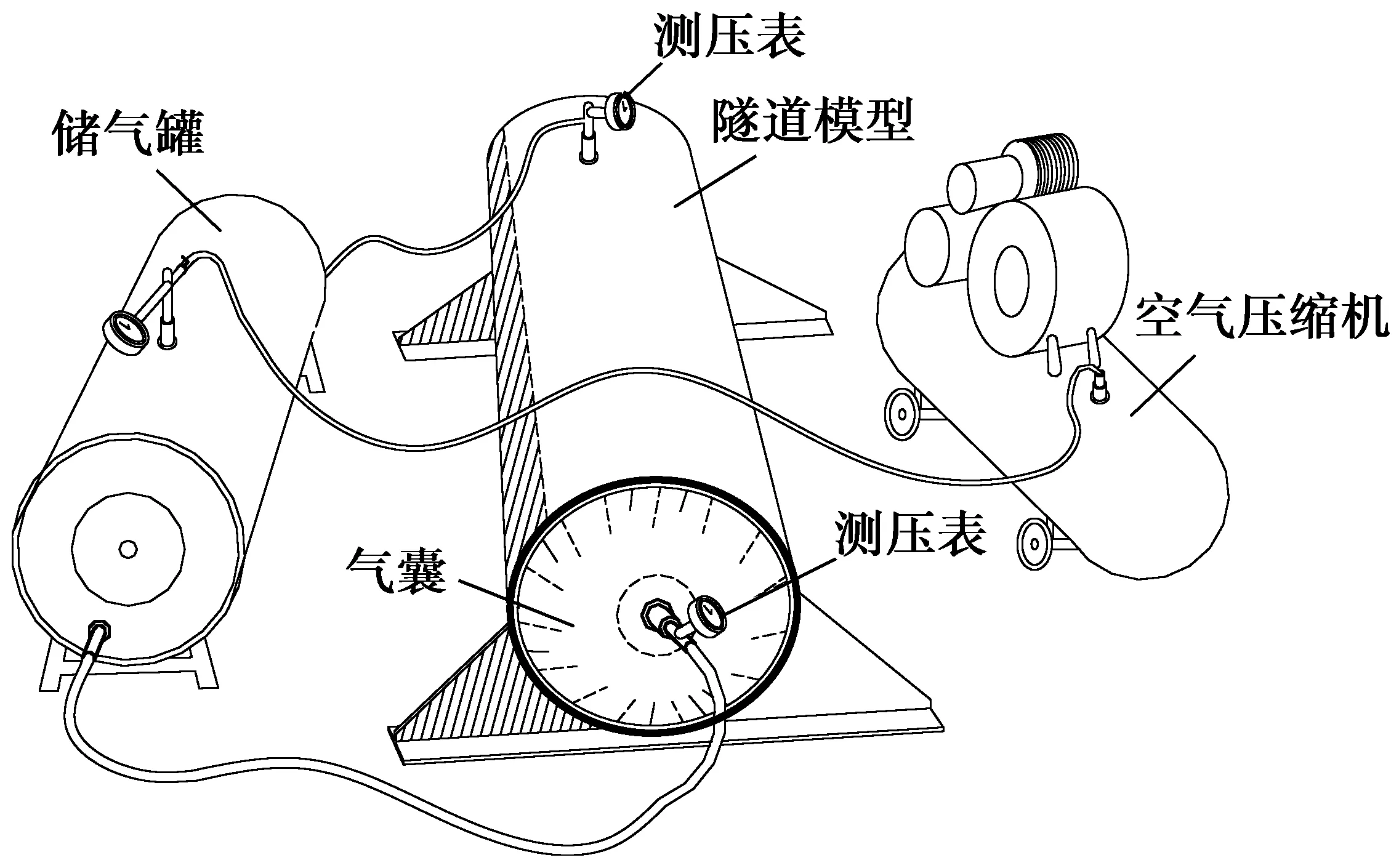
图18 充灌气囊阻漏模型试验Fig.18 Model test of plugging
2.2 试验过程
将橡胶气囊的内压p0充至50 kPa,待内压稳定后,使外部气压从零开始逐渐增大直至气囊产生较大位移,挡气失效为止。每隔20 s记录一次气囊的内压值和外压值。
2.3 试验结果
1)气囊内压与外部压力的关系 根据上文推导的三维公式,将气囊内压随外压增长变化的理论关系曲线绘制于图19,并将试验中测压表得到的数据绘制其中,由图19可知,试验数据与理论基本一致。气囊内压增长,说明气囊在外压作用下发生变形而体积减小,且内压增长幅度不大,由50 kPa增长至51.4 kPa,相应的外压从零增加至51.3 kPa。此现象证明了当外压接近内压时,气囊将滑移,阻漏失效。说明气囊正常工作的控制条件之一是外压不能大于气囊当时对应的内压。
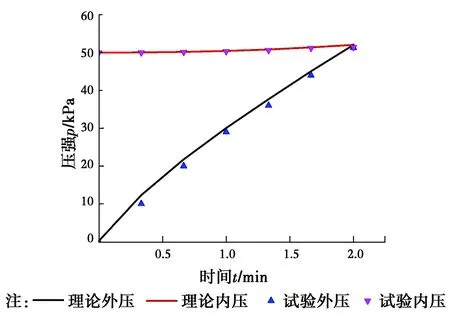
图19 外压和气囊内压随时间的增长曲线Fig.19 External and inner pressure increase with
2)外部压力与最大静摩阻力的关系 试验中,气囊从开始至失效过程中外力与最大静摩阻力的关系如图20所示。气囊最大摩阻力始终大于外力,说明此时气囊失效是因为气囊外压大于内压引起的变形失效,而非外压大于最大静摩阻力失效。即说明当气囊长度达到一定程度时,增加气囊长度并不能提高其抵挡外荷载的能力。
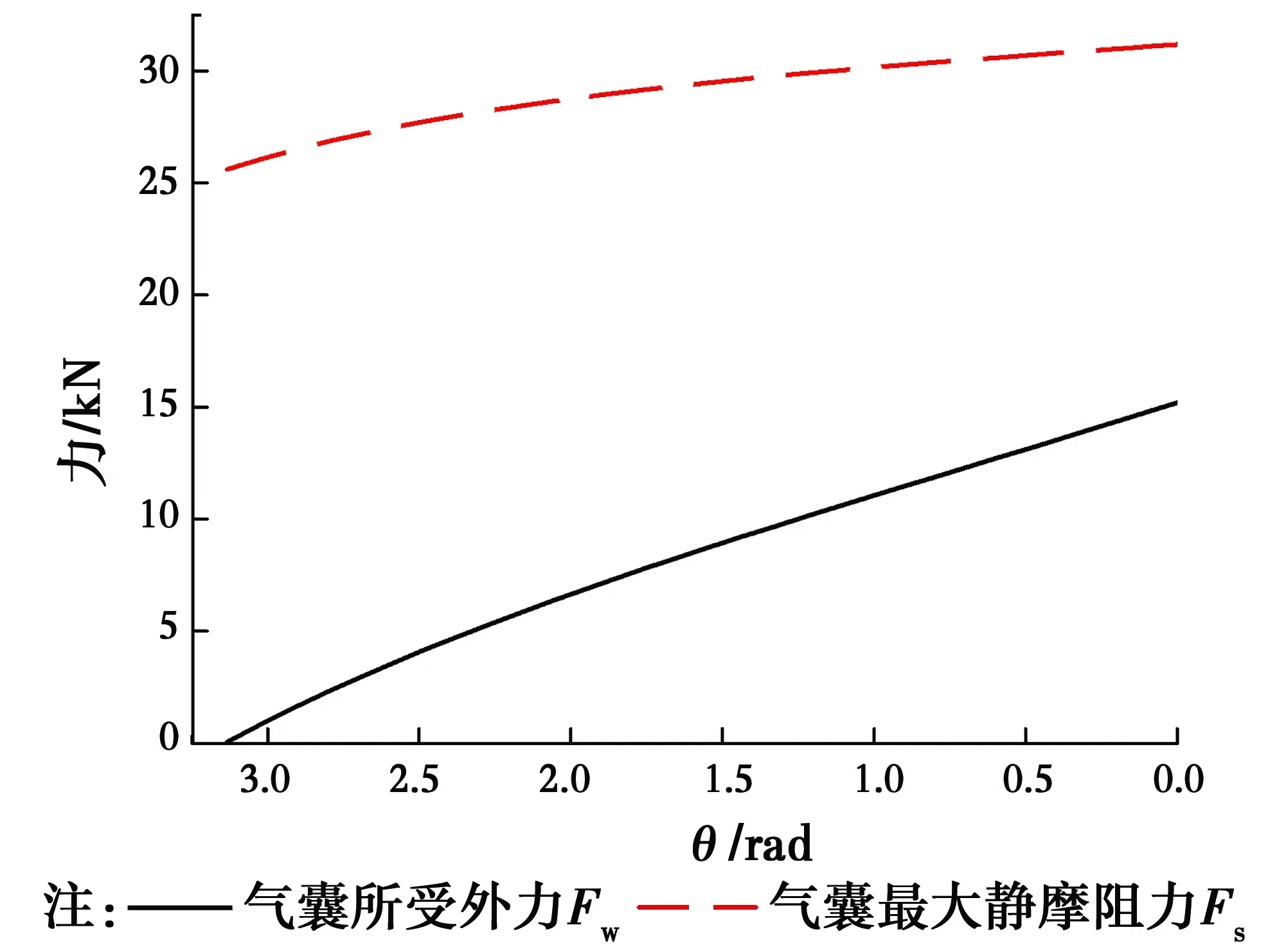
图20 外力和最大静摩阻力的变化规律Fig.20 Changes of external force and maximum static friction
3 结论
对气囊在外压作用下的形状和受力特点进行研究,得出了形状和内压随外压变化的关系。研究了气囊滑移失效的模式,探究了气囊长径比和初始压力对形状和内压变化的影响,得到了气囊能够抵挡的最大外压的计算公式。同时,模型试验的结果与理论公式有很好的一致性。主要结论如下:
1)在外压作用下,气囊受荷端逐渐扁平,自由端可保持半球形。气囊体积减小而内压增大,变形过程中,形状和内压可通过本文推导出的理论公式求得。
2)气囊能够抵挡的外压不仅与最大摩阻力有关,也与形状变化有关。只有当外压小于气囊内压时,气囊受荷端才能保持其外凸形状并且不发生滑移。
3)对比二维和三维模型,同等内压下二维模型计算得到的气囊拉力是三维结果的2倍,二维模型内压p1增长量比三维稍大,且能够抵挡的外力是三维的一半。故使用二维模型用于设计计算偏于安全,但使用三维模型更接近实际,在设计中宜考虑乘以安全系数。
4)在模型试验中,气囊失效是由于形状不能保持,其内压增长的规律与理论计算结果有很好的一致性。

