凝胶模拟液液滴碰撞的SPH数值仿真①

石 超，强洪夫，刘 虎，王 广

(1.火箭军工程大学 601室，西安 710025；2.火箭军工程大学 青州士官学院，青州 262500)

0 引言

凝胶推进剂作为一种新型火箭推进剂，与液体推进剂的主要差异在于流变特性，其剪切粘度随剪切速率的变化而变化，且一般表现出剪切变稀(假塑性)的特征[1]。凝胶推进剂雾化问题是凝胶推进技术研究的关键问题[2]，凝胶推进剂雾化效果决定了凝胶推进剂发动机的燃烧效率和燃烧稳定性。在雾化过程中，不可避免会出现液滴的碰撞聚合、反弹以及破碎过程。

为深入揭示凝胶推进剂液滴碰撞过程的物理机理，本文应用光滑粒子流体动力学(SPH)方法[3-4]，对凝胶模拟液液滴在空气中的碰撞过程进行了数值模拟，并与水滴的碰撞过程进行了对比，分析了凝胶推进剂粘性对碰撞结果的影响，以进一步揭示凝胶推进剂在雾化过程中的物理现象及内在机理。

1 流体动力学控制方程以及SPH离散

1.1 控制方程和状态方程

1.1.1 控制方程

本文流动过程可以看作不可压缩流动，不考虑热传导，拉格朗日描述下的Navier-Stokes方程为

▽·v

(1)

(2)

式中 d/dt为物质导数；ρ、p和v分别表示流体的密度、压强和速度；ν为动力粘度系数；F(s)为表面张力。

1.1.2 控制方程的SPH离散

由于本文计算涉及气液两相流动，气-液交界面处存在较大的密度、粘度梯度，传统的SPH在处理这一问题时，会引发严重的计算误差，产生诸如密度/压力震荡、粒子聚集等非物理现象。针对这一问题，Frank Ott等[5]提出，在连续性方程中，采用粒子数密度代替质量密度，表述为

▽iWij

(3)

同时，Adami等[6]提出在动量方程中，对压力和粘度系数“进行密度加权平均”，由此可保证在跨越气液两相界面时，压力项和粘性项的连续性：

(4)

其中

(5)

另外，rij为粒子i与粒子j之间的距离，μ=ρv为运动粘度系数，V=m/ρ，表示粒子的体积。F(s)表示单位质量的表面张力，具体计算式见文献[4]。

1.1.3 状态方程

为计算压强项，需引入弱可压缩状态方程[7]：

(6)

1.2 幂律型本构的SPH离散

幂律型本构模型中的剪切应力为[8]

(7)

▽v+▽vT

(8)

速度梯度▽v的SPH计算式为

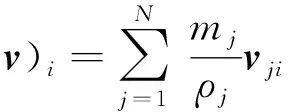
(9)

式中vji=vj-vi。

1.3 时间积分

本文采用leap-frog格式的时间积分方法[9]，即

(10)

xi(t+δt)=xi(t)+vi(t+δt/2)δt

(11)

式中φ为密度ρ及速度v；xi为粒子i的位置坐标。

2 凝胶推进剂液滴碰撞过程仿真

2.1 碰撞计算模型

凝胶推进剂射流撞击后形成的液滴在运动中将会发生碰撞，液滴碰撞是凝胶推进剂二次雾化的重要组成部分，本节以此为背景，对空气中两相同直径凝胶液滴的碰撞进行了数值模拟研究。对比研究了水滴及SC1凝胶模拟液液滴在空气中的撞击现象，空气、水及SC1模拟液的相关物性参数见表1。

本节计算中采用的液滴碰撞模型如图1所示，液滴直径D=1.6×10-4m，两液滴相对速度为vrel，偏心距离为x。

表1 计算中物质参数

对牛顿流体液滴的碰撞实验研究表明[10]，韦伯数We及碰撞参数χ对碰撞结果有重要影响：

(12)

(13)

式中ρ为液滴密度；σ为表面张力系数。

2.2 仿真结果及分析

对凝胶液滴在特定韦伯数下(We≈20、vrel=3 m/s)的正面碰撞及倾斜碰撞进行了数值模拟。其中，液滴正碰、斜碰液滴形态及粘度分布分别见图2(χ=0)和图3(χ=0.5)。

整体上看，凝胶液滴与水滴的碰撞现象具有明显区别，在该韦伯数下，水滴碰撞后会分离形成两个小液滴，而凝胶液滴粘度相对更大，撞击过程中惯性力及表面张力始终无法克服内部粘性力作用。因此，当vrel=3 m/s时，无论正碰还是斜碰，两液滴在粘性耗散下最终聚合形成一个大液滴。数值模拟结果表明，在正碰情况下，韦伯数高于45(vrel>4.5 m/s)时，SC1模拟液液滴撞击时，将出现与vrel=3 m/s时水滴撞击类似的液滴分离现象。

另外，从图2、图3可看出，在凝胶液滴内部，表观粘度的分布是不均匀的。总体来说，流动变化剧烈(即速度梯度大)的地方粘度小，这也正说明了凝胶推进剂具有“剪切变稀”的特性。

图4为液滴撞击过程中的动能变化。从图4可看出，相比水滴而言，凝胶液滴碰撞后，在粘性耗散的作用下，动能更加迅速减小，并达到稳定。

3 结论

(1)相同碰撞条件下，凝胶液滴比同尺寸水滴更易发生聚合。

(2)在高粘性作用下，碰撞后凝胶液滴的动能耗散得更快。

(3)凝胶推进剂雾化过程中，小液滴更易聚合产生大液滴，这进一步增加了凝胶推进剂雾化的难度。