基于无偏灰色马尔科夫预测WSN数据融合算法*

余修武,张 可,周利兴,张 枫,胡沐芳,刘 琴

(1.南华大学环境与安全工程学院,湖南 衡阳 421001;2.金属矿山安全与健康国家重点实验室,安徽 马鞍山 243000)

对于矿山,特别是深井矿山的恶劣环境如高温、高湿、有毒有害气体等,使得以往有线安全监测系统可靠性大大降低,增加了系统的维护成本,同时也增加了矿井的安全隐患。随着万物互联时代的到来,物联网行业正处于高速发展的时期,无线传感器网络作为物联网底层的技术支撑,广泛应用于军事侦察、医疗、环境监测、智能建筑等领域[1-3]。无线传感器网络是由许多低成本、低功耗的监测节点通过无线通信方式实现相互连接,它能在监测区域自组织成监测网络,将监测区域的环境数据通过网络上传给用户[4-5]。由于其节点能够自组织且布置简单,不需要提前布置电缆,相比于有线监测系统更加可靠,并且维护简单。因此,它能够满足矿井复杂、恶劣自然环境的安全数据监测要求。对于无线传感器网络,网络的生命周期与稳定性是它的关键,而决定生命周期的主要因素是节点的能耗,一些研究表明在网络中数据的传输占能量消耗的70%以上,因此,在保证数据可靠的前提下,如何减少数据传输量,从而减少能量的消耗,延长网络的生命周期是目前研究的重点[6-7]。

由于数据融合的方法能够有效的减少能耗,许多学者对数据融合进行了研究[8]。文献[9]通过SOMF神经网络与分簇算法结合,提取同类数据特征,从而减少数据发送量;文献[10]利用测量的误差进行分组,同时分配基本信任,再通过证据理论求得各测量值的权值,最后加权求和得到融合结果;文献[11]采用多传感器有偏估计减少最小二乘有偏估计方差,改善测量数据融合后的可靠性。

井下环境较稳定且有周期性的变化规律,在时间维度上冗余度较大。本文通过利用少量数据建立无偏灰色系统描述温度变化,再利用马尔科夫链优化预测结果,最后设置阈值在控制误差范围的同时,减少数据上传量,延长网络寿命。仿真实验验证了算法的有效性。

1 无偏灰色马尔科夫预测模型

1.1 灰色预测模型GM(1,1)

一个系统中信息的明确量可以定义为一种颜色,黑色代表内部特征或参数全部未知,白色代表内部特征或参数全部已知,内部特征与参数一部分已知,一部分未知则用灰色代表,灰色模型GM(1,1)是一阶单变量预测模型,该模型在数据预测中具有复杂度低和计算效率高的优点。该模型的表述如下:

设有原始数据序列

对原始数据进行累加得到:

生成序列:

得到灰色模型白化方程如式(1)所示:

(1)

式中:a代表发展系数,u代表灰色输入。为求解a、u构建矩阵B与Y:

(2)

经过一次累减得到n+1时刻原始序列预测值如式(3)所示

(3)

1.2 无偏灰色预测模型

根据灰色模型GM(1,1)得到参数a、u,由此可以得到无偏灰色模型GM(1,1)的参数b、A,其计算分别如式(4)、式(5)所示:

b=ln[(2-a)/(2+a)]

(4)

A=2u/(2+a)

(5)

通过计算得到b、A的值,从而得到无偏灰色模型GM(1,1)的拟合模型如下:

1.3 预测结果马尔科夫优化

马尔科夫模型根据在状态之间转化概率来预测未来状态的一种数学模型其表达式如式(6)所示:

x(n)=x(t)pn-t

(6)

式中:x(n)为n时刻该系统的状态,x(t)表示系统的初始状态,即t时刻的状态,p为每个状态对应的状态转移矩阵。

马尔科夫优化过程:首先将以往的灰色无偏预测结果与实际测量值进行对比,得到误差,根据误差进行状态划分并确定转移概率,得到马尔科夫状态转移矩阵,再利用马尔科夫状态转移矩阵修正预测数据,最后得到优化的预测数据。

状态划分:为了使所得数据适应于马尔科夫模型,使用相对误差作为其划分的标准,即利用预测值与实测值的差值来划分状态,假设该差值的取值范围在M1、Mk之间,可以把该区间划分为k个状态C1,C2,C3,…,Ck,其中第j个状态区间为[Qj,Rj](其中j=1,2,3,…,k)。状态数的取值与拟合的误差范围和样本的数据量有关,通常取3组～5组较为合适,确保每个组都有数据,且根据井下情况自行调整安全监测数据。

状态转移矩阵的构造:设所有数据分为k个状态,从状态Cj转移到下一状态Ci的概率为Pj,i则概率转移矩阵P为:

利用频率近似概率方法得到状态转移概率,如式(7)所示:

Pj,i=Nj,i/Nj

(7)

式中:Nj,i表示由状态Cj转移到状态Ci的次数,Nj为状态Cj出现的总次数,其中Pj,1+Pj,2+…+Pj,k=1。

计算马尔科夫优化预测值:设t时刻的灰色无偏预测值为X(t),马尔科夫优化后的预测值为Y(t)。根据t-1时刻的实际状态值判断t-1时刻所处状态,假设其为Ct-1状态,利用状态转移矩阵计算t时刻马尔科夫优化预测值,计算如式(8)所示:

(8)

式中:用j状态的上下边界Qj、Rj中点作为马尔科夫优化计算的参考值,P(t-1),j表示t-1时刻的状态到状态j的转移概率。

2 数据融合

算法描述:将无偏灰色马尔科夫模型与分簇式路由算法LEACH相结合,由簇内节点采集一组历史数据,根据这些数据建立灰色无偏马尔科夫预测模型并预测下一组数据,若预测值与实际值之差大于预先设定的阈值ε,则节点上传该组数据给簇头,若预测值与实际测量值之差小于ε,则不发送该组数据只更新本地数据。

为了简化描述,假设无线传感器网络满足以下几个条件:①传感器节点部署后都有唯一的内网标识ID号,且部署后不能随意移动位置;②能量无法补充,所有节点的能量都相同;③普通节点与汇聚节点数据传输是可靠的并且普通节点每轮只传输一次数据;④汇聚节点位置固定且有一定的计算能力、存储空间和能量。

本文的数据融合方法中检测节点的工作过程:采集初次数据并计算模型的参数,上传数据给簇头节点,由簇头节点将信息发送给汇聚节点,节点通过比对实测数据与预测数据的差值是否大于阈值并以此来决策是否上传与更新数据,若小于阈值则只更新本地数据,否则上传该检测周期的数据同时更新本地数据并以更新的数据重新计算模型的相关参数。具体步骤如下:

步骤1 各节点开始采集数据,判断数据是否达到建模的要求,若满足执行下一步,否则继续采集数据直到数据满足要求为止。

步骤2 根据采集的数据利用灰色无偏模型GM(1,1)求得模型参数,在此基础上对下一组数据进行预测得到初步预测结果,最后利用马尔科夫模型对预测结果进一步优化得到最终预测结果。

步骤3 比较预测结果是否接近提前预警值,若超过则更新监测密度,以更短的监测周期监测数据并上传本轮数据,否则进入步骤四。

步骤4 比较预测值与实际测量值,得到预测误差。

步骤5 比较预测误差是否大于阈值ε,大于则发送本轮数据,小于则不发送本轮数据。

步骤6 保存本周期数据,删除最早周期数据,跳转到步骤一。

3 仿真实验与结果分析

3.1 算法数据上传率对比分析

利用MATLAB进行数据仿真,实验数据来自于Intel Berkeley Research Lab数据集,该数据集记录了布置在实验室内的54个节点所采集的温度、湿度、光照等环境数据。节点的采集周期为30 s,共收集了一个月的数据。本文在其中选取了2 000个温度数据,5个一组共分为400组作为融合仿真数据。

设置不同阈值对比基于无偏灰色马尔科夫预测WSN数据融合算法(DFUGMP)、文献[12]TCDCP算法和文献[13]LRDDGO算法的数据上传率,如图1 所示。由图1可知,随着阈值的增加3种算法的数据上传率均逐渐降低,但DFUGMP算法的数据上传率始终低于TCDCP与LRDDGO算法。当阈值取0.02时,DFUGMP算法数据上传率为0.87,TCDCP与LRDDGO算法的数据上传率分别为0.92和0.93;当阈值取0.6时DFUGMP算法数据上传率为0.52,TCDCP与LRDDGO算法的数据上传率分别为0.58和0.67。因此,在相同阈值条件下DFUGMP算法所需要上传数据量更少。

图1 数据传输率与设定阈值

3.2 算法对网络能耗及寿命对比分析

为了测试算法在分簇式路由结构中对网络能耗及寿命的影响,实验采用常用的能量消耗模型,统计节点发送、接收、融合所消耗的能量。在发送数据时,若两节点距离小于d0则采用自由空间模型,若大于d0则采用多路径衰减模型。节点发送和接收的lbit数据能耗如式(9)、式(10)所示:

(9)

(10)

实验参数设置如表1所示。

图2对比了3种算法的系统寿命,由图可知DFUGMP算法在396轮出现第1个死亡节点,TCDCP与LRDDGO算法分别在356轮与302轮出现死亡节点。通常认为一个系统的节点死亡率达到50%时认为该系统失效。由图2可知DFUGMP算法在第697轮节点死亡率达到50%,TCDCP与LRDDGO算法分别在第661轮和622轮死亡50%节点。因此,DFUGMP寿命相比TCDCP与LRDDGO算法分别延长了5.4%和12.1%。

表1 参数设置

图3对比了3种算法的系统能耗,由图可以看出LRDDGO算法系统能耗下降最快,其次为TCDCP算法,下降最慢的为DFUGMP算法。DFGMP算法在第729轮系统总能量剩余10J,TCDCP与LRDDGO算法分别在第675轮和633轮剩余10 J,这说明DFUGMP算法能耗更低,能够更有效的减少上传的数据量,减少系统的能耗。

图2 系统寿命对比

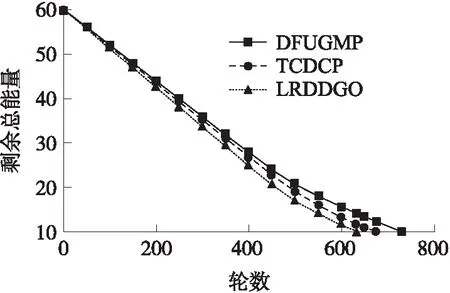
图3 系统能耗对比

4 结语

针对井下环境数据变化的时间相关性,提出基于无偏灰色马尔科夫链预测的井下安全数据融合算法。该算法利用无偏灰色马尔科夫链的预测模型来预测下一周期的安全数据,通过对比预测值与实际值的差值与设定阈值大小来判断是否上传该组数据,以此减少数据的上传率,进而减少通信所消耗的能量。仿真结果表明该融合算法有更好的预测精度和更低的数据上传率,同时整体的能耗更低,有利于延长网络寿命。在下一步的工作中将在实际环境中搭建WSN系统,对融合算法进行验证,同时对井下环境路由与定位算法进行研究。