基于形态学的连铸坯氧化铁皮测温误差校正方法*

闫俊红,李忠虎,王志春

(内蒙古科技大学信息工程学院,内蒙古 包头 014010)

连铸坯表面温度是确定二冷配水模型、优化拉坯速度的重要依据之一[1-2]。但是连铸坯表面分布有大量随时剥落的氧化铁皮,将铸坯与氧化铁皮之间的传热方式由热接触变为热辐射、热对流等,使得氧化铁皮与连铸坯表面之间存在温度梯度,形成的测温误差高达上百摄氏度。基于CCD的比色测温方法能够较好的消除环境及发射率的影响,成为连铸坯温度测量领域的研究热点[3-6],但是氧化铁皮的随时剥落严重影响CCD比色测温的精度。

为消除连铸过程中氧化铁皮产生的测温影响,Meriaudeau[7]、Liu Jun[8]等采用红外测温法,根据区域内的最大温度值确定整个区域的温度,方法简单但是误差较大,温度波动达100 ℃以上,无法克服氧化铁皮随时剥落产生的测温影响。Louhenkilpi[9]、Ma J C[10]、舒服华[11]等通过建立连铸坯凝固传热模型的方式消除氧化铁皮的测温影响,并对工艺参数进行了优化,但是离线建立的传热模型无法满足工艺参数实时变化的实际生产需要。马交成[12]、白海城[13]等采用面阵CCD测温、传热模型和数值分析相结合的方法对氧化铁皮产生的测温影响进行校正,测温误差为±10 ℃。但计算量较大,实时性要求较难满足,并且传热模型只能采用表面温度进行验证,使该方法在实际应用中遇到障碍。平均值法、延时滤波法、峰值保持法等时域方法均导致氧化铁皮的测温偏离与滞后,无法消除氧化铁皮的测温影响。基于数学形态学的膨胀算法利用空间信息一定程度上能够消除氧化铁皮的影响[14],但对于面积较大的块状氧化铁皮需要进行多次膨胀运算,造成测温曲线呈阶梯状变化,测温结果偏高。

针对氧化铁皮产生的测温误差,本文提出一种自适应数学形态学膨胀算法,构造多尺度多方向结构元素,根据氧化铁皮的形状特征及统计特性,以结构元素的边缘、旋转及比例运算为基础,采用自适应膨胀算法消除氧化铁皮导致的温度剧烈波动,减小了测温误差,提高了测温精度和稳定性。

1 连铸坯比色测温原理

由全辐射定理可知,高温辐射体的温度与CCD图像灰度值之间的关系为:

(1)

式中:A为CCD光敏单元输出电流和图像灰度值之间的转换系数;μ为光电转换系数;t为曝光时间;2a/f′是相对孔径;K是CCD光学系统透过率;ε(λ,T)是辐射体的黑度系数;C1、C2为第一、第二辐射常数;T(λ)为光谱响应特性函数;T是辐射体温度。

如果彩色CCD的光谱响应为理想冲激响应,则R、G、B三基色输出信号与温度之间的关系为:

(2)

根据比色测温原理,为了获得较宽的测温范围,选择R、G通道进行比色测温计算,其中取λr=700 nm,λg=532 nm。取式(2)中R通道和G通道相比并取对数得:

(3)

其中:

(4)

由式(3)可得连铸坯表面温度,lnKr/Kg为CCD器件响应系数,εrg为发射率影响因子。连铸生产现场高水汽、高粉尘、环境恶劣,而且连铸坯表面分布着随时剥落的氧化铁皮,因此测温过程中需根据连铸坯测温条件进行参数辨识[15-16]。假设连铸坯为黑体时对应温度值为T0,则连铸坯实际温度T与εrg和T0之间的关系为:

(5)

(6)

将C2、λg和λr代入式(5)得到式(6),由式(6)计算所得即为连铸坯实际温度。

2 自适应数学形态学膨胀算法

2.1 数学形态学膨胀算子

数学形态学是以集合论为基础的一种非线性图像处理方法,根据不同结构元素的构造实现图像中对应形状的识别和处理。数学形态学的基本运算有腐蚀、膨胀、开运算和闭运算4种。腐蚀、膨胀算法定义如下:

FΘB=min[F(x+i,y+j)-B(i,j)]
(x,y)∈DF,(i,j)∈DB

(7)

F⊕B=max[F(x+i,y+j)+B(i,j)]
(x,y)∈DF,(i,j)∈DB

(8)

开运算与闭运算分别定义如下:

F∘B=FΘB⊕B

(9)

F·B=F⊕BΘB

(10)

为了有效消除氧化铁皮产生的测温影响,本文提出一种自适应数学形态学膨胀算法。针对氧化铁皮区域形状具有闭合性特征,将结构元素的旋转运算、比例运算以及边界综合定义为结构区域,自适应膨胀算子定义如下:

F⊕B=max[F(x+i,y+j)+Bn(i,j)]
(x,y)∈DF,(i,j)∈DB[RBSB∂B]

(11)

式中:连铸坯图像标记为F,结构元素标记为B,∂B表示集合B的边界像素的集合,DF定义为F的区域,DB定义为RB、SB和∂B的集合,n为结构元素的尺度,R和S分别表示旋转和比例运算。

2.2 多尺度结构元素构造

结构元素的构造在数学形态学方法中至关重要,因为结构元素的选取与图像处理效果、系统运算速度等直接相关。结构元素尺寸过大,则系统运算时间长;结构元素单一,则处理后的图像只含有单一的方向信息,造成细节丢失。采用的结构元素合理,则能够实现图像多方向细节特征的保留。

氧化铁皮区域一般具有闭合性特征,为了实现氧化铁皮区域的准确检出,本文使用多方向多尺度结构元素,在保证测温系统速度符合生产现场实际需要的前提下,根据氧化铁皮的闭合性特征,构造尺度为3×3、5×5的8个结构元素如图1所示。

图1 结构元素

2.3 自适应增益函数

氧化铁皮一般有细小密集型和块状分布型,根据氧化铁皮的形状特征和统计特性,采用图像标准差Δ确定氧化铁皮区域,根据8个多方向结构元素,在每个方向使用多尺度结构元素,根据不同方向细节所占比重ωi,将每个方向的细节特征进行加权组合。

Δn=|f-fn|

(12)

式中:图像标准差Δn为像素点与其相邻像素的灰度差异,差异越大,则该像素为边界的可能性越大,边界与结构元素的方向相垂直时,检测效果最好。由式(12)确定氧化铁皮区域,为了得到连铸坯辐射图像多尺度层的特征,采用多尺度多方向结构元素对连铸坯图像进行自适应膨胀运算。为了尽量全面利用目标像素点及其邻域信息,并克服形态学处理产生图像灰度整体偏移的问题,本文使用了8个结构元素,选择结构元素B31,B32,B33,B34尺度为3,B51,B52,B53,B54尺度为5。不同尺度和方向的结构元素取法如下:

(13)

(14)

式中:Δl-ni为第(l-ni)个结构元的图像标准差,且∑ωni=1,ωni表示不同方向、不同尺度结构元素的权重。采用加权结构元素对氧化铁皮区域进行自适应膨胀运算,还原连铸坯表面真实温度。

3 实验结果与讨论

在国内某钢厂进行实验,对连铸二冷末端到矫直点前端部分进行温度测量,测温范围800 ℃～1 200 ℃。钢种选择Q235,钢坯尺寸为230 mm×1 500 mm,通过HY-5800A型双目彩色CCD、DS-4008HC图像采集卡、DS-8104HC-ST视频图像处理器对连铸坯图像进行采集,软件环境为VS2010+Opencv,共采集样本296个,对连铸坯图像样本进行统计分析,选取块状氧化铁皮样本。

3.1 高温连铸坯辐射图像去噪

高温连铸坯辐射图像存在粉尘、水雾、背景辐射等干扰,图像质量较差,为了实现精确测温需对辐射图像进行滤波去噪处理,但是传统的滤波处理方法对高温辐射图像并不适用[17-18]。高温连铸坯辐射图像的噪声主要包括雾状噪声、点状噪声和脉冲噪声等。其中水汽是雾状噪声的主要来源,烟尘和水汽会形成点状噪声,脉冲噪声主要是由CCD的全波段响应引起的,其中脉冲噪声是影响高温辐射图像质量的主要因素。

传统的均值滤波虽然能够去除噪声,但是会使图像模糊,而中值滤波、Gauss滤波等方法会造成连铸坯表面真实温度信息丢失。根据连铸坯高温辐射图像像素间具有强相关性,结合脉冲噪声的特点,本文采用双边滤波的方法减小噪声影响。双边滤波根据空间信息和灰度信息的非线性组合滤除噪声,滤波效果由窗口大小、空间邻近度因子、灰度相似度因子共同决定,定义如下:

(15)

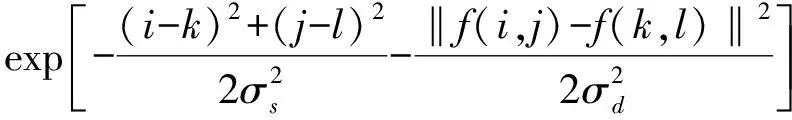
(16)

式中:(i,j)为中心点像素坐标;(i,j,k,l)为邻域像素坐标;σs为空间方差;σd为灰度方差。灰度方差的选择与高温辐射图像中噪声方差σn的估计有关,σd与测温精度直接相关,因为在高温辐射图像中灰度值与温度值直接对应,σd的取值增大,则滤波效果增强,但是图像会变模糊;σs的取值增大,则加权平均像素点增加,能够消除强噪声的影响,但是同样使图像模糊。根据高温连铸坯辐射图像的噪声特点,本文取σd=2σn,2σs=w,滤波效果如图2所示。

图2 滤波效果

由图2可知,从图像清晰度来看,均值滤波、中值滤波、高斯滤波、双边滤波依次增强,说明双边滤波算法对连铸坯高温辐射图像的处理效果优于其他滤波算法。采用均方误差MSE(Mean Square Error)和峰值信噪比PSNR(Peak Signal to Noise Ratio)对滤波去噪结果进行定量评价,其中MSE与PSNR表示为:

(17)

(18)

式中:i,j为像素点的位置坐标,i,j=1,2,…,255;M,N表示像素的行和列。4种算法滤波效果对比如表1 所示,双边滤波结果的MSE最小,PSNR最大,说明双边滤波对图像细节的保留最好,信噪比最高,具有良好的去噪性能和细节保留能力,这是因为双边滤波算法对灰度相关度、空间邻近度进行了综合考虑。

表1 滤波效果对比

3.2 多尺度多结构元素自适应膨胀算法

采用膨胀算法和本文算法对双边滤波后的连铸坯高温辐射图像进行处理,1次膨胀效果如图3(a)所示,10次膨胀效果如图3(b)所示,本文算法如图3(c)所示。

根据图像的标准差确定连铸坯高温辐射图像中氧化铁皮区域的统计特性,如表2所示。采用本文算法对图像进行处理后,标准差最小,说明氧化铁皮区域经自适应膨胀运算后被剥离,还原了连铸坯表面真实温度。

图3 氧化铁皮去除效果

表2 标准差对比

实验结果表明,多次膨胀运算的结果使非氧化铁皮区域的灰度变大,采用本文提出的算法可以将非氧化铁皮区域重新连通起来,有效去除氧化铁皮的影响。对于面积较大的氧化铁皮区域,通过判定氧化铁皮区域再进行自适应膨胀运算的方式,快速有效消除氧化铁皮区域;对于一些细小的氧化铁皮来说,根据自适应判别条件及结构元素尺度、权重的选择,去除效果明显,说明本文提出的多尺度多结构元素自适应数学形态学膨胀算法对氧化铁皮区域的处理是有效的。

3.3 比色测温实验

根据连铸坯比色测温公式(6)对图3(c)进行温度计算,对本文提出的算法进行测温验证。计算得连铸拉坯方向某一行的温度分布曲线如图4所示。

图4 连铸坯拉坯方向温度分布曲线

由图4可知,图中由下至上依次为原始温度曲线、采用本文提出算法的测温曲线和采用10次膨胀算法后的测温曲线。原始温度曲线中氧化铁皮的存在造成测温结果波动很大,最大测温误差达±50 ℃。经过10次膨胀运算后的温度曲线在同一测量点的温度值明显偏高,并且出现了阶梯状变化,最大测量误差达65.6 ℃,主要因为在采用膨胀算法消除氧化铁皮测温影响的过程中,对非氧化铁皮区域同样进行了膨胀操作,从而导致温度出现阶梯状变化,测温误差偏大,从而失去了根据连铸坯表面温度进行二冷配水控制的意义。采用本文算法使用多尺度多结构元素,在确定氧化铁皮区域的前提下,采用自适应膨胀算法,克服了过膨胀现象的产生,避免了对非氧化铁皮区域进行膨胀操作而使测量温度偏高的现象,非氧化铁皮区域的温度值保持不变,保留了连铸坯表面温度的真实信息,避免了多次膨胀带来的温度曲线阶梯状变化。将测温结果与红外测温仪的测量值进行比较,红外测温值为参考温度,如图5所示。

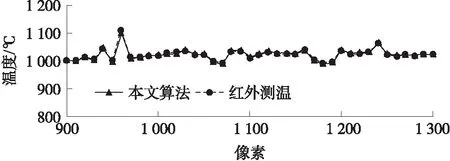
图5 连铸坯拉坯方向测温曲线对比图

最大绝对误差为±5.5 ℃,最大相对误差为0.54%,本文算法有效校正了氧化铁皮引起的测温误差,实验结果如表3所示。

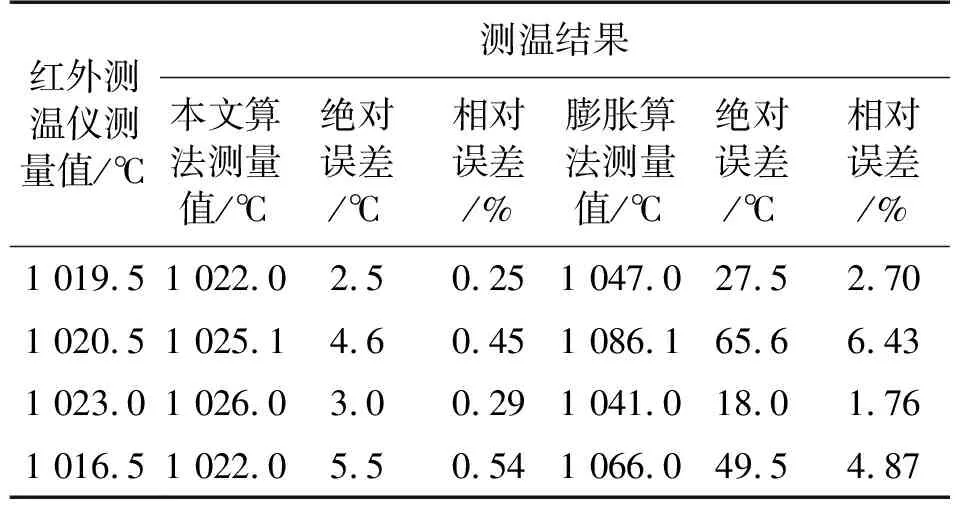
表3 Q235测量结果

4 结论

①根据连铸坯高温辐射图像的特点,采用双边滤波对连铸坯高温辐射图像进行去噪,对空间参数、灰度参数进行设置去除辐射图像中的脉冲噪声。

②提出了一种数学形态学的高温辐射图像处理算法,利用该算法对高温连铸坯辐射图像进行多尺度多结构元素自适应膨胀运算,修正了连铸坯高温辐射图像中氧化铁皮随时剥落产生的测温影响,保留了非氧化铁皮区域的真实温度信息。通过理论分析和实验证明了该算法的有效性和实时性。